J. Cent. South Univ. (2020) 27: 2032-2042

DOI: https://doi.org/10.1007/s11771-020-4428-5

Improved method for determining active earth pressure considering arching effect and actual slip surface

HE Zhong-ming(何忠明)¹, LIU Zheng-fu(刘正夫)¹, LIU Xiao-hong(刘晓红)²,BIAN Han-bing(卞汉兵)³

1. School of Traffic & Transportation Engineering, Changsha University of Science & Technology,Changsha 410114, China;

2. College of Construction and Engineering, Hunan Institute of Science and Technology,Yueyang 414006, China;

3. Laboratory of Civil Engineering and Geo-environment, University of Lille, Lille 59000, France

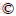Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: To determine the distribution of active earth pressure on retaining walls, a series of model tests with the horizontally translating rigid walls are designed. Particle image velocimetry is used to study the movement and shear strain during the active failure of soil with height H and friction angle φ. The test results show that there are 3 stages of soil deformation under retaining wall translation: the initial stage, the expansion stage and the stability stage. The stable sliding surface in the model tests can be considered to be composed of two parts. Within the height range of 0.82H-1.0H, it is a plane at an angle of π/4+φ/2 to the horizontal plane. In the height range of 0-0.82H, it is a curve between a logarithmic spiral and a plane at an angle of π/4+φ/2 to the horizontal. A new method applicable to any sliding surface is proposed for active earth pressure with the consideration of arching effect. The active earth pressure is computed with the actual shape of the slip surface and compared with model test data and with predictions obtained by existing methods. The comparison shows that predictions from the newly proposed method are more consistent with the measured data than the predictions from the other methods.

Key words: particle image velocimetry; retaining wall; soil arching effect; active earth pressure

Cite this article as: HE Zhong-ming, LIU Zheng-fu, LIU Xiao-hong, BIAN Han-bing, ZENG Ling. Improved method for determining active earth pressure considering arching effect and actual slip surface [J]. Journal of Central South University, 2020, 27(7): 2032-2042. DOI: https://doi.org/10.1007/s11771-020-4428-5.

1 Introduction

Accurately estimating the active earth pressure is crucial in practical engineering. However, the active earth pressure calculated by Coulomb’s method or Rankine’s method deviates from the actual pressure. To solve this problem, many scholars have conducted in-depth researches on the theoretical formula for active earth pressure. WANG [1] analyzed the stress state of a differential element of sliding soil and obtained the active earth pressure at different depths. However, this method cited the assumption of Coulomb’s surface. Several researchers improved Wang’s equation with different sliding surface shapes. YANG et al [2] and CAO et al [3] studied the formula of active earth pressure with a cycloidal slip surface. WANG et al [4] and YANG et al [5] showed that the active failure surface in soil is a logarithmic spiral when the soil is behind a vertical wall and has a horizontal face. Then, a formula was proposed to determine the active earth pressure. Although these above researchers analyzed the influence of sliding surface shapes on active earth pressure, they ignored the effect of stress redistribution on the failure surface shape and on the pressure applied to the wall.

Soil has a tendency to move downwards relative to a translating wall. Because of the shear strength of soil, the frictional resistance from a rough wall bears part of the weight of the soil and affects the direction of the principal stresses. This phenomenon means that the soil behind a rough wall can partially transfer the vertical stress to the adjacent soil, resulting in a lower stress state. TSAGARELI [6] observed the stress redistribution process through experiments, and used the phrase “arching in soils” to describe this process. HARROP-WILLIAMS [7] theoretically analyzed the influence of soil arching on active earth pressure and suggested that the trajectory of the minor principal stress σ₃ is portrayed as a catenary, similar to a circular trajectory. FANG and ISHIBASHI [8] conducted a series of experiments with typical wall action modes. The experimental data showed that the active earth pressure is irregularly distributed. The data also indicated that the pressure within a certain range near the surface is greater than the pressure in the static state due to the soil arching effect. At present, scholars simplify slip surface shapes and the effect of soil arching so that they can theoretically analyze the active earth pressure with the consideration of the arching effect. GOEL and PATRA et al [9] comparatively studied the active earth pressure with different configurations of slip surface shapes and soil arching shapes. PAIK and SALGADO et al [10] discussed the effect of soil arching and proposed a method to estimate active earth pressure with the assumptions that the failure surface of a mass forms a plane at π/4+φ/2 to the horizontal and that the arch shape was circular. Based on the study of PAIK, KHOSRAVI et al [11, 12] improved a formula of active earth pressure applicable to the case in which the backfill behind a vertical wall was subjected to vertical loading and indicated that slip surface of the soil is related to the wall height. ZHOU et al [13] and ZHOU et al [14] calculated active earth pressure with a parabolic arch and planar slip surface. RAO et al [15] proposed an active earth pressure method after assuming that the sliding surface of the soil was a plane and that the soil arch formed a part of the circle. However, the flaw of such studies is that the predicted failure surfaces in the soil were different from the actual failure surfaces.

In recent years, researchers have used particle image velocimetry(PIV) [16-19] to monitor the deformation of soil and achieved satisfactory results. NIEDOSTATKIEWICZ et al [20], KHOSRAVI et al [21] and PATEL et al [22] studied the deformation and shear strain of the soil behind a retaining wall under three motion modes based on PIV; NAZHAT et al [23] and AUBRAM [24] used PIV to observe the deformation and shear strain of soils under vertical loading. PIV has great application potential. It can also be used in other fields such as deformation of nanomaterials [25] in subgrade engineering or geotechnical seepage analysis [26, 27].

For the purpose of considering the influence of slip surface shape in the calculation of earth pressure, a set of experiments is designed in this paper. The active failure process of soil in the model test is observed by PIV, and the shape of the slip surface is discussed. A method applicable to any slip surface is deduced for calculating active earth pressure. In this method, the trajectory of σ₃ is considered to be circular. According to the shape of the slip surface, the theoretical data were contrasted to the experimental data and the data calculated by previously proposed theories.

2 Model tests

2.1 Test model design

The size of the model box in this test is 120 cm (length)×40 cm (width)×70 cm (height). The box is welded by high-strength steel. The retaining wall is connected to the motors. By adjusting the stroke of the three-phase asynchronous motor, different inclination and action modes of the retaining wall can be achieved. The model box has slots for placing the rigid frame so that the fixed boundary can be simulated at different positions. The front of the box is 16 mm thick tempered glass, through which the soil deformation can be observed. Holes are excavated in the center of the wall, along the vertical direction, and five high-precision earth pressure cells are arranged in these holes. The size of the model box and the layout of the cells are portrayed in Figure 1.

2.2 Soil properties and test arrangement

The backfill soil used in the experiment is yellow dried Dongting Lake sand. The uniformity coefficient C_u is 2.90, and the coefficient of curvature C_c is 1.41. The percentage content of each particle size is listed in Table 1.

To ensure the uniformity of the soil, the soil is added to the model box layer by layer: the weight of each layer of soil is first calculated, assuming a certain density; then, the soil is laid evenly and slightly compact to a specified height; finally, soil is added in the box to a height of 40 cm. After 24 h, some soil is sampled for direct shear testing to determine its material parameters. The properties of the soil are summarized in Table 2. The wall friction angle is tested by the method in Ref. [28]. To determine this angle as accurately as possible, the vertical pressures applied in the direct shear test are 0.5P, 1.0P, 1.5P and 2.0P (P is the maximum active earth pressure obtained from Coulomb’s formula). The four test configurations are placed in Table 3.

2.3 Data acquisition

The data collected during the test include displacement data and earth pressure data. The displacement is obtained from the pictures taken by the high-definition (HD) camera during the PIV processing. The displacement can be transformed to get the soil shear strain. With the calibration curve, the earth pressure is acquired through the electrical signal received from the cyy-55 multichannel data acquisition instrument. The photography interval and the earth pressure data collection interval were set to 5.0 s, and the deformation and earth pressure data were collected at every 0.1 mm of retaining wall translation.

Before the test, the camera and the earth pressure cells record data in a static state, then, the movable retaining wall is slowly moved to the left at a fixed speed of 0.02 mm/s. The retaining wall stops panning after 600 s, the camera and the earth pressure stop acquiring data after 650 s.

3 PIV data analysis

3.1 Displacement and shear strain analysis

Through PIV analysis of the deformation photos, the displacement of the soil with different width:height ratios is obtained. Taking test A2 as an example (width:height ratio n=0.7), the relative displacement (that is, the movement of the soil in a collection interval) and the total displacement are shown in Figures 2 and 3 below.

Figure 2 shows that when the retaining wall moves horizontally, a slight displacement first occurs in the upper left corner. Then, the displacement area expands to the bottom and the fixed side. Finally, the maximum relative displacement of the soil mass appears in the upper left corner, near the retaining wall. There are 3 stages in the process of soil displacement during the movement of the retaining wall. The initial stage: At the beginning of the movement (0-75 s), the gradient surface of the relative displacement of the soil is generally flat. At the expansion stage (75-300) s, the sliding surface accommodating the relative displacement in the middle and lower areas begins to shift to the rigid frame side; the relative displacement surface in the upper middle areas slightly contracts to the side of the movable baffle while the sliding surface in the upper areas exhibits little change. The stability stage: When t>300 s, the relative displacement surface of the soil tends to be stable; ultimately, an “s”-shaped surface is formed.

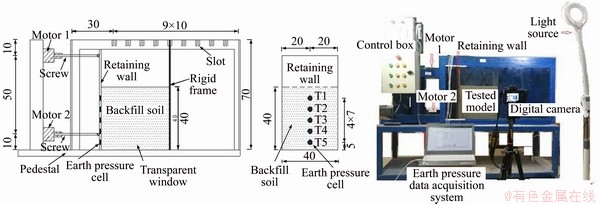
Figure 1 Model size and test system(unit: cm)

Table 1 Percentage content of each particle size in backfill soil

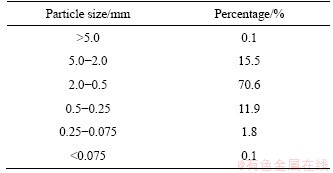
Table 2 Properties of tested soil

Table 3 Configurations of four tests

The total displacement is the accumulation of the relative displacement, so the change law of the total displacement is basically consistent with the relative displacement. However, comparing Figures 2 and 3, the change in total displacement lags behind that in the relative displacement. The soil forms a stable relative displacement surface around t=300 s, while the stable total displacement surface is formed near t=400 s.

Figure 2 Relative displacement of soil at different time (n=0.7):

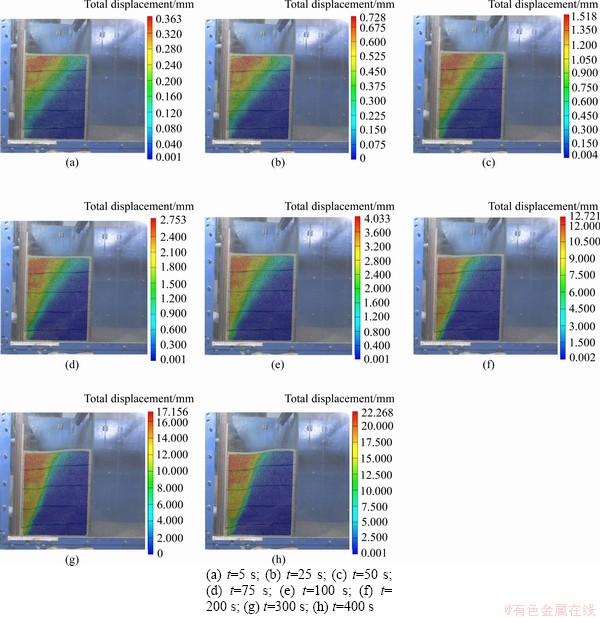
Figure 3 Total displacement of soil at different time (n=0.7):

The diagram of shear strain obtained from the transformation of the soil displacement is shown in Figure 4. The development of the soil shear strain corresponds to three stages of displacement change. During the initial stage (0-75 s), the region of shear strain crosses the bottom of the retaining wall, which is an observation similar to that described in Ref. [21]. In the expansion stage (75-300 s), the shear strain in the middle and lower areas of the soil further increases, while the upper part of the soil gradually differentiates into two relatively indistinct shear strain surfaces: one is the curved surface extending along the trend of the middle and lower part of the shear strain surface, and the other is a plane at an angle of approximately π/4+φ/2 to the horizontal plane. Then, in the upper soil, the curved slip surface dissipates gradually, and the straight slip surface expands continuously. Finally, in the stability stage (>300 s), the shape of the slip surface accommodating the soil shear strain does not change significantly.

3.2 Sliding surface analysis

The distribution of the shear strain (such as the shear strain in the first stage) is not obvious when the displacement of the retaining wall is small, so the stable sliding surface formed by the shear strain in the third stage is selected as the representative sliding surface of the soil. Figure 5 shows the shear strain surface of the soil with different width:height ratios n, which is stable (t=400 s) in the process of active failure.

The slip surfaces of different tests are shown in Figure 6, with toe of the wall as the origin (0,0) of the coordinate system. The sliding surface of each test shown in Figure 6 does not extend to the rigid frame, and all the sliding surfaces have basically the same shapes, indicating that the soil behind the retaining wall can be considered to have a semi infinite width when n≥0.6.

Figure 4 Shear strain of soil at different times (n=0.7):

Figure 5 Shear strains at different width-to-height ratios n:

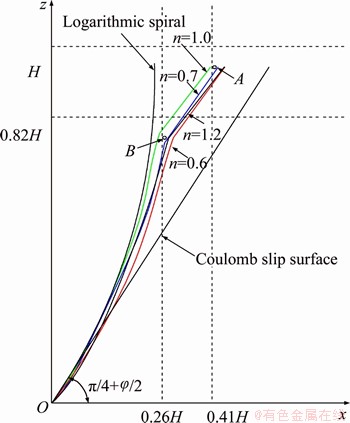
Figure 6 Shear strain curves of soil mass for different width-to-height ratios n (H=40 cm)

Each sliding surface is divided into two parts: a plane and a curved surface. It is assumed that the intersection of the plane and the top surface of the soil is point A; point B is common to the plane and the curved surface. Then, the distance between point A and the movable retaining wall is 15.9- 16.6 cm. The intersection point B is 10.6-11.3 cm from the movable baffle and 7.4-8.1 cm from the top surface of the soil mass.

The average value of each curve is taken as the sliding surface when the semiinfinite soil is in active failure. Expressing these data with height H, the sliding surface is π/4+φ/2 from the horizontal surface in the range of 0.82H-1.0H, and the sliding surface in the height range of 0-0.82H is a curve between the Coulomb slip surface and logarithmic spiral [4].

4 Analysis of active earth pressure

4.1 Equation for active earth pressure

When the soil slides against a translation wall, the soil-wall interface angle △ rotates the principal stress of the soil. A schematic diagram of this stress rotation is illustrated in Figures 7 and 8, where φ is the internal friction, ε is the inclination of retaining wall, H is the height of tested soil, f(x, z) is the sliding surface, σ₁ is the major principal stress and σ₃ is the minor principal stress; the trajectory of σ₃ takes the form of arc [7].

Figure 7 Schematic diagram of stress rotation

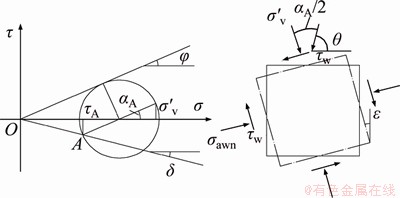
Figure 8 Mohr’s circle of stress at point A in Figure 7

The horizontal stress σ_h and vertical stress σ_v at any point D are written as:

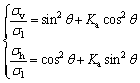                    (1)

where θ is the angle between σ₁ and the horizontal direction of point D. The Rankine’s coefficient of lateral active earth pressure K_a is:

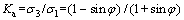              (2)

The vertical force dV at point D is:

      (3)

where dA is the width of the shaded element at point D, and R is the radius of the σ₃ trajectory.

The relationship between R and the width of the horizontal differential element L_z is:

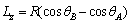                     (4)

where θ_A and θ_B are the angles between σ₁ and the horizontal direction at point A and point B, respectively. θ_A and θ_B are written as:

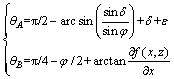               (5)

The expression of the coefficient of lateral active earth pressure K_awn is:

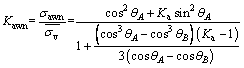      (6)

where 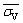is the average vertical stress and σ_awn is the active lateral stress.

Figure 9 shows the stress state of the horizontal differential element at a certain depth z, where dW is the self-weight of the element and ω is the angle between the tangent of the slip surface and the x-coordinate.

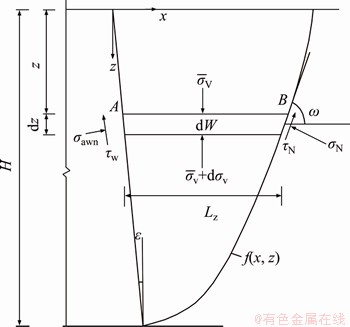
Figure 9 Horizontal differential element behind retaining wall

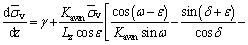
All the forces in the vertical direction exerted on the element are satisfied by Eq.(7):

                     (7)

where γ is the unit weight of the soil.

Some scholars [10-15] assume that the sliding surface is a plane and then derive the expression of active earth pressure from Eq. (7). However, when the sliding surface is a complex curve, the analytical solution of Eq. (7) is difficult to calculate, so this paper uses the difference method to approximate the solution. First, the sliding soil is divided into horizontal strips with thicknesses of △z, as shown in Figure 10. It is assumed that within the scope of a single horizontal strip, the stresses applied to the retaining wall and the slip surface are constant. L_z and ω take the values at the midpoint of the horizontal strip.

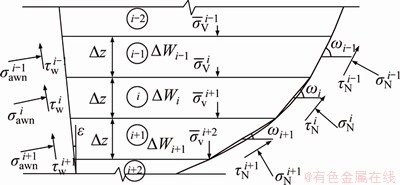
Figure 10 Stress of horizontal soil strip

Then Eq. (7) can be rewritten as:

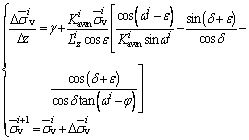     (8)

The active lateral stress and shear stress applied on the wall can be easily obtained:

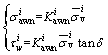                        (9)

The resultant earth pressure E and overturning moment M are calculated according to Eq. 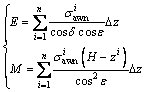(10).

                  (10)

where n is the number of horizontal strips divided, zⁱ is the vertical distance between the center of the strip and the upper surface of the soil, and the vertical distance h from the action point of the resultant force to the lower end of wall is:

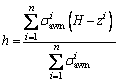                      (11)

4.2 Active earth pressure analysis

As portrayed in Figure 11, the actual sliding surface in the range of 0-0.82H is simplified into a plane. In the calculation of theoretical pressure with Eq. (8), the slip surface is the combination of the actual slip surface (part 1) and simplified slip surface (part 2). The boundary condition is where z=0. The value of △z is 0.5 mm, which can guarantee the calculation accuracy.

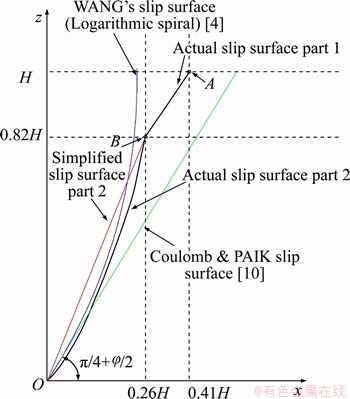
Figure 11 Slip surfaces used in different calculation methods (H=40 cm)

The theoretical pressure and the measured pressure are portrayed in Figure 12. The relationship between active earth pressure and the depth is clearly nonlinear. The theoretical data are basically consistent with the measured data, which indicates that the calculation method of active earth pressure based on the actual sliding surface is reasonable and reliable. There is a certain deviation between the theoretical earth pressure and the real value, which is mainly due to the nonuniform distribution of the mechanical parameters of the soil with depth, and the shape of the soil arch is not completely consistent with the assumptions in this paper.

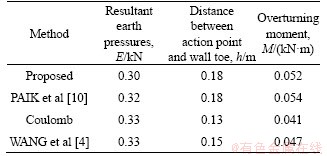
The earth pressure calculated by the new method is compared with the Coulomb solution, Paik’s solution [10] and Wang’s solution [4] in Figure 13. The resultant earth pressure and action point are listed in Table 4.

The comparison between Figures 12 and 13 shows that the active earth pressure from the new method is more consistent with the measured data than with the results of the other methods. The distribution law of earth pressure calculated by Eq. (8) is basically the same as Paik’s solution, and the locations of the maximum earth pressure strength are also consistent. Due to the difference in the sliding surface shapes, the calculated maximum earth pressure and resultant earth pressure in this paper are 15.1% and 6.2% smaller than those of Paik’s solution, respectively. Compared with Wang’s solution, which does not consider the soil arching effect, the resultant earth pressure calculated in this paper is approximately 10% smaller, and the action point is significantly higher than that determined with Wang’s solution. The overturning moment of the earth pressure is slightly less than that determined with Paik’s solution, but significantly greater than Coulomb’s solution or Wang’s solution.

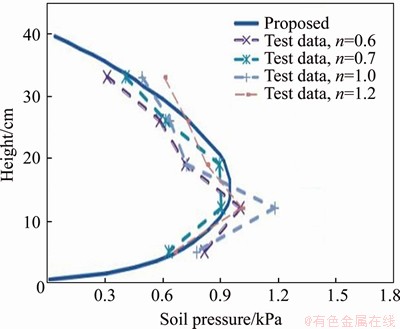
Figure 12 Comparison of calculated and measured earth pressures

Figure 13 Active earth pressures obtained by different calculation methods

Table 4 Different methods of determining active earth pressure

5 Conclusions

Model tests are conducted to observe soil deformation and measure active earth pressure. The research conclusions of this article are summarized as follows:

1) The deformation and shear strain in the failure process of the soil are divided into three stages: the initial stage, the expansion stage and the stability stage.

2) The slip surface of noncohesive soil of a semiinfinite width under active failure lies between a plane at π/4+φ/2 to the horizontal and the logarithmic spiral. The actual sliding surface in the model tests can be divided into two parts: a plane at an angle of π/4+φ/2 to the horizontal in the height range of 0.82H-1.0H, and a curve through the lower end of the wall in the height range of 0-0.82H.

3) An equilibrium equation of active earth pressure suitable for any slip surface is derived with the consideration of soil arching and a differential solution for this equation is proposed.

4) The rationality of the new method is verified by a comparison of earth pressure results that were predicted with the new method, experimentally measured and predicted with other theories mentioned in this paper. Compared with the prediction of the other theories mentioned in this paper, the pressure calculated with the new method is closer to the measured value.

References

[1] WANG Y Z. Distribution of earth pressure on a retaining wall [J]. Geotechnique, 2000, 50(1): 83-88. DOI: 10.1680/ geot.2000.50.1.83.

[2] YANG Gui, WANG Yang-yang, LIU Yan-chen. Analysis of active earth pressure on retaining walls based on curved sliding surface [J]. Rock and Soil Mechanics, 2017, 38(8): 2182-2188. DOI: 10.16285 /j.rsm.2017.08.004. (in Chinese)

[3] CAO Zhen-ming．Active earth pressure analysis on retaining wall with sliding surface of filling curve [J]. China Journal of Highway and Transport, 1995, 8(1): 7-14. DOI: 10.19721/ j.cnki.1001 7372. 1995. s1. 002. (in Chinese)

[4] WANG Kui-hua, MA Shao-jun, WU Wen-bing. Active earth pressure of cohesive soil backfill on retailing wall with curved sliding surface [J]. Journal of Southwest Jiaotong University, 2011, 46(5): 732-738. DOI: 10.3969/j.issn.0258- 2724.2011.05.004. (in Chinese)

[5] YANG Ming-hui, DAI Xia-bin, ZHAO Ming-hua, LUO Hong. Calculation of active earth pressure for limited soils with curved sliding surface [J]. Rock and Soil Mechanics, 2017, 38(7): 2029-2035. DOI: 10.16285/j.rsm.2017.07.024. (in Chinese)

[6] TSAGARELI Z V. Experimental investigation of the pressure of a loose medium on retaining walls with a vertical back face and horizontal backfill surface [J]. Soil Mechanics and Foundation Engineering, 1965, 2(4): 197-200. DOI: https://doi.org/10.1007/BF017 06 095.

[7] HARROP-WILLIAMS K. Arch in soil arching [J]. Journal of Geotechnical Engineering, 1989, 115(3): 415-419. DOI: 10.1061/(ASCE)0733-9410(1985)111:3(302).

[8] FANG Y S, ISHIBASHI I. Static earth pressures with various wall movements [J]. Journal of Geotechnical Engineering, 1986, 112(3): 317-333. DOI: 10.1061/(ASCE)0733-9410 (1986)112:3(317).

[9] GOEL S, PATRA N R. Effect of arching on active earth pressure for rigid retaining walls considering translation mode [J]. International Journal of Geomechanics, 2008, 8(2): 123-133. DOI: 10.1061/ (ASCE)1532-3641(2008)8:2(123).

[10] PAIK K H, SALGADO R. Estimation of active earth pressure against rigid retaining walls considering arching effects [J]. Geotechnique, 2003, 53(7): 643-654. DOI: 10.1680 /geot.2003.53.7.643.

[11] KHOSRAVI M H, PIPATPONGSA T, TAKEMURA J. Theoretical analysis of earth pressure against rigid retaining walls under translation mode [J]. Soils and Foundations, 2016, 56(4): 664-675. DOI: 10.1016/j.sandf.2016.07.007.

[12] KHOSRAVI M H, KARGAR A R, AMINI M. Active earth pressures for non-planar to planar slip surfaces considering soil arching [J]. International Journal of Geotechnical Engineering, 2018: 1-10. DOI: 10.1080/ 19386362.2 018.1503439.

[13] ZHOU Y T, CHEN Q, CHEN F. Active earth pressure on translating rigid retaining structures considering soil arching effect [J]. European Journal of Environmental and Civil Engineering, 2018, 22(8): 910-926. DOI: 10.1080/19648189. 2016.1229225.

[14] ZHOU Q Y, ZHOU Y T, WANG X M. Estimation of active earth pressure on a translating rigid retaining wall considering soil arching effect [J]. Indian Geotechnical Journal, 2018, 48(3): 541-548. DOI: 10.1007/s40098- 017-0252-8.

[15] RAO P, CHEN Q, ZHOU Y, NIMBALKAR S, CHIARO G. Determination of active earth pressure on rigid retaining wall considering arching effect in cohesive backfill soil [J]. International Journal of Geomechanics, 2015, 16(3): 1-9. DOI: 10.1061/(ASCE)GM.1943-5622.0000589.

[16] WHITE D J, TAKE W A, BOLTON M D. Soil deformation measurement using particle image velocimetry (PIV) and photogrammetry [J]. Geotechnique, 2003, 53(7): 619-631. DOI: 10.1680/geot.53.7.619.37383.

[17] WHITE D, RANDOLPH M, THOMPSON B. An image-based deformation measurement system for the geotechnical centrifuge [J]. International Journal of Physical Modelling in Geotechnics, 2005, 5(3): 1-12. DOI: 10.1680/ ijpmg. 2005.050301.

[18] MAHMOUDIMEHRIZI M, DAGHIGH Y, NAZARIAFSHAR J. Physical modeling of the helical anchor walls’ behavior using particle image velocity [J]. Indian Geotechnical Journal, 2019: 1-17. DOI: 10.1007/ s40098-019-00397-z.

[19] SALEHI ALAMDARI N, KHOSRAVI M, KATEBI H. Distribution of lateral active earth pressure on a rigid retaining wall under various motion modes [J]. International Journal of Mining and Geo-Engineering, 2020, 54(1): 15-25. DOI: 10.22059/ ijmge.2019.280916.594805.

[20] NIEDOSTATKIEWICZ M, LESNIEWSKA D, TEJCHMAN J. Experimental analysis of shear zone patterns in cohesionless for earth pressure problems using particle image velocimetry [J]. Strain, 2011, 47: 218-231. DOI: 10.1111/j.1475-1305.2010.00761.x

[21] KHOSRAVI M H, PIPATPONGSA T, TAKEMURA J. Experimental analysis of earth pressure against rigid retaining walls under translation mode [J]. Géotechnique, 2013, 63(12): 1020-1028. DOI: 10.1680/geot.12.P.021.

[22] PATEL S, DEB K. Study of active earth pressure behind a vertical retaining wall subjected to rotation about the base [J]. International Journal of Geomechanics, 2020, 20(4): 402-408. DOI: 10.1061/(ASCE)GM.1943-5622. 0001639.

[23] NAZHAT Y, AIREY D. The kinematics of granular soils subjected to rapid impact loading [J]. Granular Matter, 2015, 17(1): 1-20. DOI: 10.1007/s100 35-014-0544-y.

[24] AUBRAM D. Development and experimental validation of an arbitrary Lagrangian-Eulerian (ALE) method for soil mechanics [J]. Geotechnik, 2015, 38(3): 193-204. DOI: 10.1002/gete.20140 0030.

[25] ZENG L, XIAO L Y, ZHANG J H, FU H Y. The Role of Nanotechnology in Subgrade and Pavement Engineering: A Review [J]. Journal of Nanoscience and Nanotechnology, 2020, 20: 4607-4618. DOI:10.1166/jnn.2020.18491.

[26] ZHANG J H, LI F, ZENG L, PENG J H, LI J. Numerical simulation of the moisture migration of unsaturated clay embankments in southern China considering stress state [J]. Bulletin of Engineering Geology and the Environment, 2020: 1-10. DOI : 10.1007/s10064-020-01916-6.

[27] ZENG L, YAO X F, ZHANG J H, GAO Q F, CHEN J C, GUI Y T. Ponded infiltration and spatial-temporal prediction of the water content of silty mudstone [J]. Bulletin of Engineering Geology and the Environment, 2020: 1-12. DOI: 10.1007/s10064-020-01880-1.

[28] YING Hong-wei, ZHANG Jin-hong, WANG Xiao-gang, LI Bing-he, ZHU Wei. Experimental analysis of passive earth pressure against rigid retaining wall under translation mode for finite soils [J]. Chinese Journal of Geotechnical Engineering, 2016, 38(6): 978-986. DOI: 10.11779/ CJGE2016 06002.(in Chinese)

(Edited by HE Yun-bin)

中文导读

考虑土拱效应和滑裂面影响的主动土压力计算方法

摘要：为研究挡土墙主动土压力分布规律，本文开展了刚性挡土墙平动模型试验，利用颗粒图像测速技术研究高度为H、内摩擦角为φ的无黏性土体在主动破坏过程中的位移和剪应变发展规律。试验结果表明，挡土墙发生平移时的土体变形可划分三个阶段：初始阶段，发展阶段和稳定阶段。稳定阶段的土体滑裂面由两部分组成，在0.82H~1.0H高度范围内，滑裂面为与水平面成π/4+φ/2的平面，在0~0.82H高度范围内的滑裂面为曲面，该曲面处在对数螺旋面和与水平面成π/4+φ/2的平面所夹区域之中。本文考虑土拱效应，基于差分法提出了适用于任意滑裂面形状的主动土压力计算方法，并根据实际滑裂面计算了土体主动土压力理论值。在此基础上，将本文方法得到的理论值与实验数据及其他方法计算的理论值进行对比，验证了本文所提出方法的有效性。

关键词：粒子图像测速；挡土墙；土拱效应；主动土压力

Foundation item: Projects(51978084, 51678073) supported by the National Natural Science Foundation of China; Project(2020JJ4605) supported by the Natural Science Foundation of Hunan Province, China; Project(2019IC13) supported by the International Cooperation and Development Project of Double First-Class Scientific Research in Changsha University of Science & Technology, China

Received date: 2020-04-19; Accepted date: 2020-05-30

Corresponding authors: LIU Zheng-fu, PhD Candidate; Tel: +86-13974865995; E-mail: 597073225@qq.com; ORCID: 0000-0001- 8178-2152