概率方法在恢复力模型参数识别中的应用分析
刘佩，袁泉，魏庆朝
(北京交通大学 土木建筑工程学院，北京，100044)
摘要：考虑模型和模型参数的不确定性，应用贝叶斯概率方法通过实测数据对恢复力模型参数进行识别。首先，推导得到模型参数的负对数似然函数表达式，建立基于贝叶斯理论的恢复力模型参数识别计算框架；其次，根据密肋复合墙体在低周反复荷载作用下所得滞回曲线，建立针对该类型墙体的用于识别的恢复力模型；最后，以2种加载方式下的2块比例为1/2的密肋复合墙体试件的实测滞回数据为例，基于贝叶斯理论识别得到恢复力模型参数的最有可能值和协方差矩阵，分析模型选取的依据和模型误差对反应预测的影响。研究结果表明：由模型参数最有可能值得到的滞回曲线与实测值较吻合，验证了识别结果的合理性；采用贝叶斯概率方法可以定量的确定模型参数的不确定性，为后续计算分析提供依据。
关键词：参数识别；贝叶斯理论；密肋复合墙体；恢复力模型
中图分类号：TU311 文献标志码：A 文章编号：1672-7207(2013)09-3843-06
Application of a probabilistic approach to restoring force model parameter identification
LIU Pei, YUAN Quan, WEI Qingchao
(School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)
Abstract: Taking into account the uncertainty of model and model parameters, a Bayesian probabilistic approach was applied for parameter identification of restoring force model using tested data. Negative log-likelihood function of model parameters was derived. Bayesian computational frame for parameter identification of restoring force model was proposed. According to the tested hysteresis curves of multi-grid composite walls under low cyclic loadings, a restoring force model for multi-grid composite walls was proposed for identification. The most probable values and covariance matrixes of restoring force model parameters of two multi-grid composite wall specimens of 1/2 scale whose cyclic loading histories were different were identified based on the tested data. The rules for model selection and effect of model error on response prediction were analyzed. The results show that the hysteresis curves obtained through the most probable values without considering the model prediction errors agree well with those tested ones, which validates the identification results. Through Bayesian probabilistic approach, quantitative uncertainty of model parameters is obtained, which can be used for further analysis.
Key words: parameter identification; Bayesian theorem; multi-grid composite walls; restoring force model
结构识别是对模拟结构响应与实测数据之间的差距进行极小化运算，进而识别出结构参数的过程。一般来说，结构识别计算需采用某种分析模型来构造参数估计问题，此分析模型包含一系列作为识别参数的待估计参数，对待识别结构的当前状态进行描述。由于所选定的结构模型并不是真实的结构，所以，结构模型误差总是存在的，并且对于结构模型参数来说，没有真实值，结构模型参数及模型误差都是不确定的。基于贝叶斯理论的模型参数识别方法不仅能给出参数的最有可能值，而且能得到定量描述模型参数不确定性的协方差矩阵。Beck等[1]首先将贝叶斯理论引入系统参数识别研究中，建立了基于贝叶斯理论的参数识别框架。基于贝叶斯理论的模型参数识别方法目前主要应用于采用实测环境振动数据的线性结构的模态参数识别中[2-6]。本文以恢复力模型为例，将贝叶斯理论扩展应用到已知实测数据时非线性模型参数的识别中。恢复力模型可以用于模拟钢筋混凝土结构在强震作用下的滞回特性。针对钢筋混凝土构件恢复力模型的研究，比较有代表性的有三线性退化Takeda模型[7]、Nogami等[8]提出的一种考虑极限荷载后强度降低的恢复力模型和Ozcebe等[9]提出的一种考虑滑移捏拢现象的恢复力模型。没有一种恢复力模型适用于所有结构或构件及不同的加载方式，选取1种恢复力模型对结构进行计算分析时，需要考虑选取的恢复力模型的不确定性。系统识别法是确定恢复力模型参数的一种途径。Lu[10]以钢筋混凝土柱的振动台试验数据为基础，建立了误差函数，通过自适应步随机搜索优化算法识别了恢复力模型的参数值；Loh等[11]将修正的Bouce-Wen模型和系统识别过程应用于振动台测试数据来评估模型参数；Kunnath等[12]提出了一种可用来确定钢筋混凝土结构连续光滑型滞回模型参数的系统识别法，该方法以修正的Gauss-Newton方法为基础。这些识别方法只能得到模型参数的最优值，并不能得到模型参数的不确定性。在此，本文作者首先建立基于贝叶斯理论的非线性模型参数识别计算框架；其次，根据密肋复合墙体在低周反复加载下所得滞回曲线，提出1种针对该墙体的用于识别的恢复力模型；最后，根据贝叶斯理论及2块密肋复合墙体试件的实测滞回曲线数据，对2块试件的恢复力模型参数进行识别，并对贝叶斯概率方法的特性及识别结果进行分析。
1 基于贝叶斯理论的非线性模型参数识别方法
根据贝叶斯理论，若已知实测数据
，n为数据点数，则模型参数
的后验分布为
(1)
其中：
为似然函数；
为先验分布；
，为正规化常数。
若实测数据点数足够多，则似然函数比先验分布对更敏感。通常假定先验分布为常数，则后验分布正比于似然函数：
(2)
通常在计算中，采用负对数似然函数更方便，即
(3)
(4)
若实测数据足够多并且为全局可识别问题，则负对数似然函数可以通过泰勒二阶展开式进行估计：
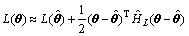(5)
其中：
为最有可能值；
为在处负对数似然函数的Hessian矩阵。在处式(5)的一阶项消失，将式(5)代入式(4)，后验分布可以通过高斯分布进行估计：
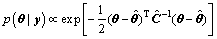(6)
其中：
为后验协方差矩阵。
假定实测数据为
，模型计算值为
，则
(7)
其中：
为模型误差。假定在不同的测点处为独立同分布的均值为0，标准差为
的高斯分布。则似然函数为
(8)
负对数似然函数为
(9)
对式(9)的求一阶导数并令其等于0，可得模型误差方差的最有可能值为
(10)
对式(10)进行优化求解，若通过matlab的fminsearch函数，则可得模型参数的最有可能值，进而根据后验协方差的定义，可得模型参数的定量的不确定性。
2 密肋复合墙体的恢复力模型
密肋复合墙体试件CW1~CW4在水平低周反复荷载作用下得到的实测滞回曲线见图1，其中，CW4为标准密肋复合墙体试件。CW1~CW3对比标准试件肋梁和肋柱数量发生改变，有关试件的具体描述见文献[13]。试验时首先施加竖向荷载，稳定后施加水平荷载：单调加载至预测极限荷载后，转为由位移控制，以预测极限荷载对应位移的倍数控制加载，每级循环3次至试验结束。
密肋复合墙体试件CW5-CW7在水平低周反复荷载作用下得到的实测滞回曲线见图1，其中CW5为标准密肋复合墙体试件，CW6为轻钢龙骨密肋复合墙体试件，CW7为加固过的受损密肋复合墙体试件，有关试件的具体描述见文献[14-15]。试验时，首先施加竖向荷载，稳定后施加水平荷载：预测屈服荷载前，按10 kN递增施加荷载，每级循环1次，预测屈服荷载后，按预测屈服荷载对应的位移±3，±4和±5 mm等至试验结束。
从图1可以看出：各试件均发生剪切破坏；试件出现了明显的刚度退化、强度退化、滑移和捏拢现象。根据以上现象，本文提出一种适用于剪切破坏的密肋复合墙体的恢复力模型，见图2。这种模型假定达到极限荷载之前骨架曲线为双线性。模型的控制参数为屈服前刚度k1，屈服后刚度k2，屈服荷载fy及其对应位移xy，极限荷载fu及其对应位移xu。考虑极限荷载后强度降低现象的参数△d，并考虑滑移捏拢现象的参数△p和△s。
模型假定：(1) 达到极限荷载前，前一次循环结束之后再加载时和反向加载时，直线指向前一次循环的最大变形点；(2) 达到极限荷载后，前一次循环结束之后再加载时和反向加载时，直线指向由前一次循环的最大变形点与△d之和对应的位移及极限荷载确定的点的位置处；(3) 正向卸载及反向卸载直线通过考虑滑移捏拢参数轴正负△s位置前刚度为k1，之后指向力轴的考虑滑移捏拢参数负正△p位置处。该模型的滞回曲线共由13类直线组成。
图1 密肋复合墙体滞回曲线
Fig.1 Hysteretic curves of multi-grid composite walls
图2 密肋复合墙体的恢复力模型
Fig.2 Restoring force model of multi-grid composite walls
3 模型参数识别计算分析
3.1 模型的选取
若选取过于简单的模型，则模型不能很好地模拟可能出现的实际反应；但是，也不能过分寻求能够完美解释实测数据的模型，否则，就会出现数据过配的情况。根据贝叶斯理论，即使1个模型的计算结果与已知数据符合得很好，也不能代表这个模型就是最好的模型，因为这个模型本身的可能性(即先验概率)也许很低。本文提出的恢复力模型只是可以用于模拟密肋复合墙体反应的恢复力模型中的一种，通过模型误差来考虑选取该模型对计算结果的影响。
3.2 最有可能值
本文识别了2种加载方式下2块标准密肋复合墙体试件CW4和CW5的恢复力模型参数值。根据试验数据直接确定试件的极限荷载，需识别的密肋复合墙体恢复力模型参数为
。该问题是1个有7个参数的优化问题，模型估计误差标准差σ的最有可能值可以通过前6个参数的最有可能值的计算表达式得到。优化过程取参数的容许误差为10-4，函数的容许误差为10-4。改变优化过程模型参数的初始值，所得结果收敛，识别问题为全局可识别类型。模型参数最有可能值的具体计算结果见表1。从表1可见：CW5的模型误差σ比CW4的小。
根据恢复力模型参数的最有可能值不考虑模型误差计算得到的滞回曲线见图3。从图3可见：计算值与实测值较吻合，验证了识别结果的合理性；特别是CW5的计算值与对应的实测值的吻合度比CW4的高，因为计算滞回曲线未考虑模型误差；而CW5的模型误差比CW4的小。
表1 恢复力模型参数的最有可能值
Table 1 Most probable values of restoring force model parameters
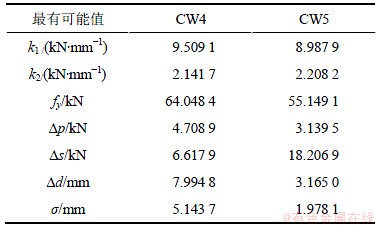
图3 试验滞回曲线与不考虑模型误差的计算滞回曲线
Fig.3 Tested and computed hysteretic curves without taking into account of model errors
CW5的模型误差比CW4的小，是因为加载方式及采集的数据点数量不同。用于识别CW5恢复力模型参数的试验数据点数为560个，而用于识别CW4恢复力模型参数的试验数据点数为305个。CW5的模型参数受先验分布的影响比CW4的要小，更符合先验分布的假定。在模型参数个数相同的情况下，较多数据点比较少数据点识别得到的模型误差小，这也充分表明基于贝叶斯理论的识别方法依赖于已知数据的特性。
3.3 变异系数
Hessian矩阵的元素可表示为
。当负对数似然函数没有解析表达式时，可通过有限差分法计算Hessian矩阵。Hessian矩阵应为正定矩阵，即其特征值大于0，才可由式(10)得到参数的极小值(全局可识别问题即为最有可能值)；并且采用有限差分法计算Hessian矩阵时，需满足变换步长时计算结果收敛的要求。经计算，2块试件均满足上述要求。
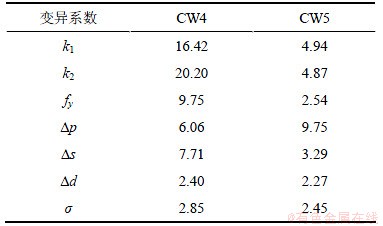
通过Hessian矩阵可计算得到协方差矩阵，进而得到描述恢复力模型各参数不确定性的变异系数(各参数的标准差与最有可能值的比值)见表2。由表2可以看到：CW4的变异系数k2最大；对于试件CW5，识别得到的△p的变异系数最大。最有可能值通过变异系数描述其与真实值接近的定量的不确定性，变异系数最大，则说明该参数的最有可能值具有最大的不确定性。
3.4 识别结果在后续计算中的应用
对于本文所提恢复力模型，若将极限荷载后强度降低现象通过将曲线指向上一循环的最大荷载降低一定的量与最大变形确定的位置表示，则同样可以作为用来模拟密肋复合墙体反应的恢复力模型。这2种模型都可以用来模拟构件的反应，但要对这2种模型识别结果的差别定量化，需要应用基于贝叶斯理论的模型选择方法进行确定，以便决定模拟构件反应时每种模型的权重。而基于贝叶斯理论识别得到的模型参数的最有可能值及协方差矩阵可以为后续模型选择计算提供便利。
另外，对结构进行可靠度分析时，除考虑结构所受激励的不确定性外，所选模型的不确定性也是影响计算结果的重要因素。考虑模型不确定性比直接将结构参数考虑为随机变量对可靠度计算结果造成的影响大很多。根据贝叶斯理论的识别结果生成样本，可以定量考虑模型误差对可靠度计算结果的影响。
表2 恢复力模型参数变异系数
Table 2 Coefficients of variance of restoring force model parameters %
4 结论
(1) 应用贝叶斯概率方法通过实测数据对恢复力模型参数进行了识别。首先，建立了基于贝叶斯理论的非线性模型参数识别计算框架；其次，根据密肋复合墙体在低周反复荷载作用下所得滞回曲线，建立了针对该类型墙体的用于识别的恢复力模型；最后，以2种加载方式下的2块1/2比例密肋复合墙体试件的实测滞回数据为例，基于贝叶斯理论对恢复力模型参数进行了识别。
(2) 识别结果包括模型参数的最有可能值和定量的不确定性。通过由模型参数最有可能值得到的滞回曲线和实测值的对比，验证了识别结果的合理性。通过对识别结果的分析，指出了模型选取应考虑模型误差的影响；模型误差对计算结果的影响较大；识别结果依赖于所采用的数据。
(3) 通过贝叶斯概率方法进行模型参数识别可以定量确定模型和模型参数的不确定性，识别结果可用于后续的模型选择方法研究及考虑模型误差的可靠度计算等。
参考文献：
[1] Beck J L, Katafygiotis L S. Updating models and their uncertainties. I: Bayesian statistical framework[J]. Journal of Engineering Mechanics, 1998, 124(4): 455-461.
[2] Yuen K V, Katafygiots L S. Bayesian time-domain approach for modal updating using ambient data[J]. Probabilistic Engineering Mechanics, 2001, 16(3): 219-231.
[3] Katafygiots L S, Yuen K V. Bayesian spectral density approach for modal updating using ambient data[J]. Earthquake Engineering and Structural dynamics, 2001, 30(8): 1103-1123.
[4] Au S K, Zhang F L. On assessing the posterior mode shape uncertainty in ambient modal identification[J]. Probabilistic Engineering Mechanics, 2011, 26(3): 427-434.
[5] Au S K. Fast Bayesian FFT method for ambient modal identification with separated modes[J]. ASCE Journal of Engineering Mechanics, 2011, 137(3): 214-226.
[6] Au S K, Zhang F L. Ambient modal identification of a primary-secondary structure by fast Bayesian FFT method[J]. Mechanical Systems and Signal Processing, 2012, 28(4): 280-296.
[7] Takeda T, Sozen M A, Neilsen N N. Reinforced concrete response to simulated earthquakes[J]. ASCE Journal of Structural Engineering, Division, 1970, 96(12): 2557-2573.
[8] Nogami Y, Murono Y, Sato T. Nonlinear hysteresis model considering strength degradation by cyclic loading for RC members[J].QR of RTRI, 2008, 49(4): 227-231.
[9] Ozcebe G, Saatcioglu M. Hysteretic shear model for reinforced concrete members[J]. Journal of Structural Engineering, 1989, 115(1): 132-148.
[10] Lu X L. Application of identification methodology to shaking table tests on reinforced concrete columns[J]. Engineering Structures, 1995, 17(7): 505-511.
[11] Loh C H, Mao C H, Huang J R, et al. System identification and damage evaluation of degrading hysteresis of reinforced concrete frames[J]. Earthquake Engineering and Structural Dynamics, 2011, 40(6): 623-640.
[12] Kunnath S K, Mander J B, Lee F. Parameter identification for degrading and pinched hysteretic structural concrete systems[J]. Engineering Structures, 1997, 19(3): 224-232.
[13] 张杰. 密肋复合墙板受力性能及斜截面承载力实用设计计算方法研究[D]. 西安: 西安建筑科技大学土木工程学院, 2004: 9-17.
ZHANG Jie. Mechanical property study and practical oblique section design method study on multi-ribbed composite wall[D]. Xi’an: Xi’an University of Architecture and Technology. School of Civil Engineering, 2004: 9-17.
[14] 姚谦峰, 李挺, 郭猛, 等. 密肋轻钢龙骨复合墙体的抗剪性能[J]. 天津大学学报, 2011, 44(7): 587-592.
YAO Qianfeng, LI Ting, GUO Meng, et al. Shear bearing capacity on multi-ribbed composite wall with light-gauge steel[J]. Journal of Tianjin University, 2011, 44(7): 587-592.
[15] 郭猛, 袁泉, 李鹏飞, 等. 加气混凝土砌块置换加固受损密肋复合墙抗震性能试验研究[J]. 四川大学学报:工程科学版, 2011, 43(1): 51-57.
GUO Meng, YUAN Quan, LI Pengfei, et al. Seismic performance experimental research for multi-ribbed composite wall strengthened with aerated concrete blocks[J]. Journal of Sichuan University: Engineering Science Edition, 2011, 43(1): 51-57.
(编辑 陈灿华)
收稿日期：2012-09-12；修回日期：2012-11-23
基金项目：国家自然科学基金青年科学基金资助项目(51208030)；北京交通大学人才基金资助项目(C12RC00040)
通信作者：刘佩(1982-)，女，河北晋州人，博士，讲师，从事可靠度理论与参数识别方法研究；电话：010-51684952；E-mail: liupei0130@126.com
