基于Hoek-Brown非线性极限平衡法的边坡安全系数
李文渊，吴启红
(成都大学 城乡建设学院，四川 成都，610106)
摘要：为了建立Hoek-Brown非线性准则下边坡安全系数计算的极限平衡法，通过理论推导与Hoek-Brown参数相对应的等效黏结力和内摩擦角，得到Hoek-Brown准则中简化Bishop极限平衡法计算边坡的安全系数公式，并分析Hoek-Brown参数对于边坡安全系数的影响，研究结果表明：岩体材料的等效黏结力与弱化因子D呈线性关系，而与岩体地质强度指标IGS、完整岩石单轴抗压强度σci和完整岩石参数mi呈非线性关系；等效内摩擦角与各Hoek-Brown参数均呈非线性关系。随D的增大，边坡安全系数F线性减小；随IGS的增大，F非线性增大；当σci较小时，F和σci关系呈现一定非线性特征，当σci较大时，二者呈现线性关系特征；F随mi的增大，呈先减小后增大的趋势。
关键词：Hoek-Brown；极限平衡法；边坡；安全系数；参数分析
中图分类号：TU457 文献标志码：A 文章编号：1672-7207(2013)06-2537-06
Factor of safety of slope based on nonlinear Hoek-Brown limit equilibrium method
Li Wenyuan, Wu qihong
(School of Urban and Rural Construction, Chengdu University, Chengdu 610106, China)
Abstract: In order to establish the limit equilibrium method of the safety factor calculation for slope stability, based on the nonlinear Hoek-Brown criterion, the Hoek-Brown parameters corresponding to the equivalent cohesion and internal friction angle were obtained through theoretical deduction, and the safety factor of the slope by simplify Bishop limit equilibrium method based on Hoek-Brown criterion was obtained. The analysis of effect of Hoek-Brown parameters on the safety factor of slope was carried out. The results show that the material equivalent cohesion and damage factor have a linear relationship, and the equivalent friction angle with the rock mass, geological strength index IGS, intact rock uniaxial compressive strength σci and integrity mi of rock parameters shows a nonlinear relationship. With the increase of D, the slope safety factor F decreases linearly; as IGS increases, F increases nonlinearly. When σci is small, F and σci shows certain nonlinear characteristic, when σci is large, they show linear relationship characteristics. As mi increases, F decreases first and then increases.
Key words: Hoek-Brown; limit equilibrium method; slope; safety factor; parametric analysis
边坡稳定性分析是工程防灾减灾的重要研究领域，计算边坡的安全系数是边坡稳定性分析的重要内容[1]。边坡稳定性分析是一个超静定问题，无法直接由静力平衡条件得出边坡的安全系数。为了回避岩土的复杂应力应变关系并将超静定问题转化为静定问题，需对边坡的稳定性分析问题进行适当近似假定，使问题变得静定可解，从而形成了极限平衡分析方法[2-4]。这种处理方法使问题的严密性受到了一定的降低害，但是，对计算结果的精度影响并不大，并且其优点是显而易见的，如使分析计算工作简化从而减少计算时间，因而在工程中获得广泛应用。极限平衡方法的基本特点是：只考虑静力平衡条件和土的Mohr-Coulomb破坏准则，也就是说，通过分析土体在破坏那一刻的力的平衡来求解。但是，对于岩体的描述，Mohr-Coulomb准则有一定的局限性，如不能解释低应力区对岩体的影响[5-6]、只能反映岩体的线性破坏特征等。为了克服以上缺点，Hoek和Brown通过大量岩石试验资料和岩体现场试验结果进行统计分析得出了Hoek-Brown准则，它能反映岩体的固有特点和非线性破坏特征以及岩石强度、结构面组数、所处应力状态对岩体强度的影响，符合边坡岩体的变形特征和破坏特征[7]，提出后受到国际工程地质界的普遍关注，并得到广泛应用。因此，一些学者建立了基于Hoek-Brown准则边坡稳定性数值分析方法[8-10]，但数值方法计算边坡安全系数耗费的时间太长。而作为边坡安全系数计算的传统方法，极限平衡法有着计算简便性的优点，却还未与Hoek-Brown准则相结合。基于以上考虑，本文作者通过理论推导，建立Hoek-Brown准则中极限平衡法计算边坡的安全系数公式，并研究Hoek-Brown参数对边坡安全系数的影响。
1 理论推导
1.1 安全系数的定义
目前采用的安全系数主要有3种[11-12]：(1) 强度储备安全系数，其通过降低岩土体强度来得到边坡的安全系数；(2) 超载储备安全系数，通过增大外部荷载计算边坡的安全系数；(3) 下滑力超载储备安全系数，即只增大边坡的下滑力而不改变相应的抗滑力计算滑坡推力设计值。极限平衡法主要采用强度储备安全系数的概念。
1952年，Bishop提出了著名的适用于圆弧滑动面的“简化Bishop法”[1]。在该方法中，边坡沿着某一滑裂面滑动的安全系数Fs1定义为，将土的抗剪强度指标降低Fs1倍 (c0/Fs1和tanf0/Fs1)后，则岩土体沿着此滑裂面处于极限平衡状态，即，
(1)
式中：τ和σ分别为滑动面上的剪应力和正应力；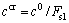
；
；c0和f0分别为边坡原始状态下的黏结力和内摩擦角；ccr和fcr分别为边坡极限平衡状态下的黏结力和内摩擦角。
上述将强度指标的储备作为安全系数定义的方法具有明确的物理意义。安全系数的定义根据滑动面的抗滑力与下滑力之比得到，该定义经过多年来的实践被国际工程界广泛承认，这种安全系数只是降低抗滑力，而不改变下滑力。同时，用强度储备安全系数定义也比较符合工程实际情况，许多边(滑)坡的发生常常是由于外界因素引起岩土体强度降低而导致岩土体滑坡[14]。
1.2 Hoek-Brown等效极限平衡法
简化Bishop 法作为极限平衡条分法的一种不受滑裂面的形状限制，并具有较高的精度，计算结果与严格的条分法十分接近[13]，在工程实际中得到广泛应用，因此，本文采用简化Bishop 法计算安全系数。简化Bishop法提出了3个假设条件：(1) 滑裂面上的实际切向力为抗剪强度发挥的那一部分；(2) 忽略条间竖向剪切力；(3) 土体屈服条件满足Mohr-Coulomb准则。计算边坡安全系数的模型如图1所示，通过推导，可得边坡安全系数[14]：
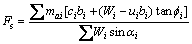(2)
其中：
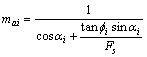(3)
式中：Fs为边坡的安全系数；ci和fi为滑动面所在土层的黏结力和内摩擦角，若对于均质边坡，则黏结力和内摩擦角为常数；ui为作用在土条i滑动面上的孔隙水压力；bi为土条宽度；αi为土条底部坡角；Wi为土条i的重力，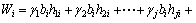
；k为滑动面所在土层的编号；γj为第j层岩土体重力密度；hji为土条i在第j层岩土体中的高度。
从式(1)可知：若建立Hoek-Brown强度参数与Mohr-Coulomb强度参数之间的关系，通过参数替换可得到Hoek-Brown准则中简化Bishop极限平衡法计算边坡的安全系数。因此，首先推导Hoek- Brown准则和Mohr-Coulomb准则之间的关系。
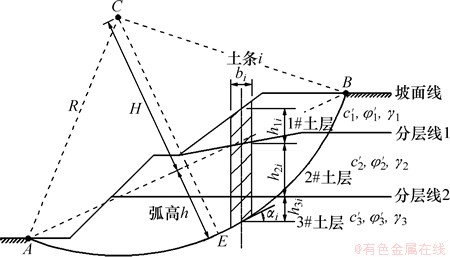
图1 边坡安全系数理论推导模型
Fig. 1 Slope safety factor theoretical model
Hoek-Brown准则表达式[5]为：
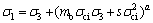(4)
式中：σ1为岩体破坏时的最大主应力；σ3为作用在岩体上的最小主应力；σci为完整岩石单轴抗压强度；mb为岩体常数，与完整岩石的mi有关；s和a取决于岩体特性的系数；这些参数均可表述为地质强度指标IGS的函数，具体形式如下：
(5)
(6)
(7)
式中：D为岩体弱化因子，与岩体的开挖方式及扰动程度有关，取值为0~1，0代表未扰动状态。
对式(4)两边求导：
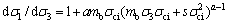(8)
利用式(8)得到采用主应力表示的剪应力和正应力[15]，
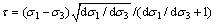(9)
(10)
根据Mohr-Coulomb准则，有
，
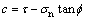，利用式(4)，式(9)和式(10)生成一系列σ1和σ3的数据点，然后对得到的曲线进行拟合[5](如图2)，最后，推导岩体等效内摩擦角和黏结力为：
(11)
(12)
式中，
；
；
；
；
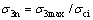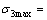
；γ为岩体容重；H为坡高；σcm表征岩体强度，
。
将图2转化成强度包络图3，可知：Hoek-Brown 强度包络线是曲线，而等效Mohr-Coulomb 强度包络线是直线。将图3分为3个区域[16]，分别记为区域1、区域2和区域3，当正应力在区域1或3时，等效Mohr-Coulomb 强度参数将会高估岩体的剪切强度，当危险滑面底部的正应力大部分都集中在区域1或3时，利用等效Mohr-Coulomb强度参数计算所得的安全系数将偏危险。通过以上推导，将式(11)和式(12)代入式(2)即可得到Hoek-Brown准则中的简化Bishop极限平衡法计算边坡的安全系数。
图2 Hoek-Brown准则和Mohr-Coulomb准则的最大主应力和最小主应力关系
Fig. 2 Relationships between major and minor principal stresses for Hoek-Brown and Mohr-Coulomb criterion
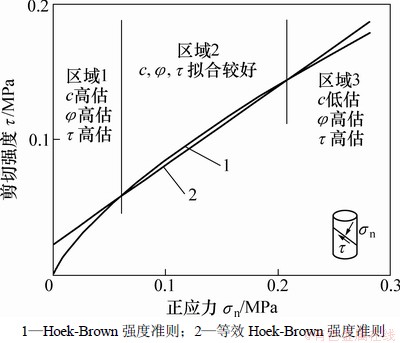
图3 Hoek-Brown 和等效Mohr-Coulomb 强度包络线
Fig. 3 Envelopes of Hoek-Brown and equivalent Mohr-Coulomb criteria
2 算例分析
2.1 模型介绍
某边坡高为20 m，坡比为1:0.5，为方便讨论，建立均质边坡模型，如图4所示。基准计算参数为：容重为γ=25.0 kN/m3，mi=17，D=0.5，IGS=50，σci=95.0 MPa。
图4 计算模型
Fig. 4 Calculation model
2.2 计算分析
分别改变各参数mi=2~32，D=0~1，IGS=5~95，σci=5~185 MPa，通过式(11)和式(12)，可计算得到相应的Mohr-Coulomb参数：黏结力c和内摩擦角f。图5~图8所示为Hoek-Brown参数D，IGS，σci和mi与黏结力c以及内摩擦角f的关系，从图5~8可以看出：随着岩体损伤因子D的增大，岩体材料的等效黏结力和内摩擦角也逐渐减小，并且黏结力与D的关系呈现线性关系，而内摩擦角与D的关系呈现非线性特征；内摩擦角和黏结力与IGS的关系均呈现非线性特征，并且随着IGS的增大，岩体材料的黏结力逐渐增大，而内摩擦角呈现先增大后减小的趋势；随着σci的增大，黏结力呈现线性增大趋势，而内摩擦角呈现非线性增大趋势，并且内摩擦角与σci关系曲线的斜率随σci的增大而逐渐减小，说明σci较小时，内摩擦角受到σci影响的敏感度较高；随着mi的增大，黏结力呈现非线性减小的特征，而内摩擦角呈现非线性增大的特征，即黏结力和内摩擦角受到mi影响的趋势相反。
图5 D和黏结力以及内摩擦角的关系
Fig. 5 Relationship among D and cohesion and friction angle
图6 IGS和黏结力以及内摩擦角的关系
Fig. 6 Relationship among IGS and cohesion and friction angle
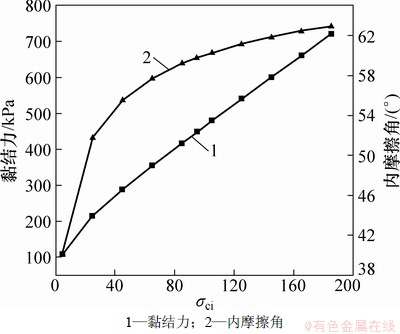
图7 σci和黏结力以及内摩擦角的关系
Fig. 7 Relationship among σci and cohesion and friction angle
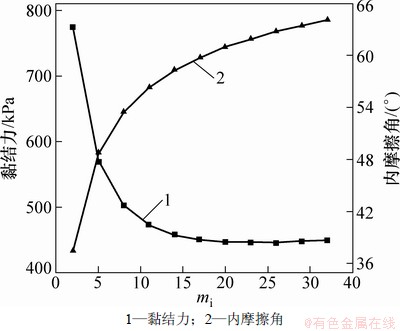
图8 mi和黏结力以及内摩擦角的关系
Fig. 8 Relationship among mi and cohesion and friction angle
图9 Hoek-Brown各个参数与边坡安全系数F之间的关系
Fig. 9 Relationship among Hoek-Brown parameters and slope safety factor F
图9所示为各个参数与边坡安全系数F之间的关系，从图9可以看出：随D的增大，F呈线性减小，可采用方程F=-4.918·(D-1.920)进行拟合；随着IGS的增大，F呈非线性增大，可采用指数方程
进行拟合，并且当IGS＞60时，F的增加幅度较大，明显高于其他参数变化对应的F；当σci较小时，F和σci关系呈现一定非线性特征，σci较大时，二者呈现线性关系特征，可采用方程
进行拟合，拟合结果高度相关；mi随F的增大，呈现先减小后增大的趋势，可采用方程
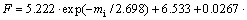
进行拟合，拟合结果较好。
3 结论
(1) 通过理论计算与Hoek-Brown参数相对应的等效黏结力和内摩擦角，得到Hoek-Brown参数D，IGS，σci和mi与黏结力以及内摩擦角的关系。
(2) 采用等效黏结力c和内摩擦角f，建立Hoek-Brown准则中简化Bishop极限平衡法计算边坡的安全系数公式，该方法方便可行，具有实用价值。
(3) 岩体材料的等效黏结力与弱化因子D呈线性关系，而与岩体地质强度指标IGS、完整岩石单轴抗压强度σci和完整岩石参数mi呈现非线性关系；等效内摩擦角与各Hoek-Brown参数均呈现非线性关系。
(4) 随D的增大，边坡安全系数F线性减小；随IGS的增大，F非线性增大；当σci较小时，F和σci关系呈现一定非线性特征，σci较大时，二者呈现线性关系特征；F随mi的增大，呈先减小后增大的趋势。
参考文献：
[1] YANG Xiaoli, SUI Zhirong. Seismic failure mechanisms for loaded slopes with associated and non-associated flow rules[J]. Journal of Central South University of Technology, 2008, 15(2): 276-279.
[2] 张倬元, 王士天, 王兰生. 工程地质分析原理[M]. 北京: 地质出版社, 1994: 67-78.
ZHANG Zhuoyuan, WANG Shitian, WANG Langsheng. Engineering geological analysis mechanism[M]. Beijing: Geology press, 1994: 67-78.
[3] Leshchinsky D. Slope stability analysis: Generalized approach[J]. Geotech Eng, 1990, 116(5): 851-867.
[4] Chen Z Y, Shao C M. Evaluation of minimum factor of safety in slope stability analysis[J]. Canadian Geotechnical Journal, 1988, 25(4): 735-748.
[5] Hoek E, Carranza-Torres C, Corkum B. Hoek-Brown failure criterion–2002 Edition[C]//Proc NARMS-TAC Conference, Toronto, 2002: 267-273.
[6] Hoek E, Brown E T. Empirical strength criterion for rock mass[J]. Journal of the Geotechnical Engineering Division, ASCE, 1980, 106(9): 1013-1035.
[7] YANG Xiaoli, YIN Jianhua. Slope stability analysis with nonlinear failure criterion[J]. Journal of Engineering Mechanics, 2004, 130(3): 267-273.
[8] 林杭, 曹平, 李江腾, 等. 基于广义Hoek-Brown准则的边坡安全系数间接解法[J]. 煤炭学报, 2008, 33(10): 1147-1151.
LIN Hang, CAO Ping, LI Jiangteng, et al. The indirect calculation method for the safety factor of slope based on generalized Hoek-Brown criterion[J]. Journal of China Coal Society, 2008, 33(10): 1147-1151.
[9] 林杭, 曹平, 李江腾, 等. 基于Hoek-Brown准则的三维边坡变形稳定性分析[J]. 岩土力学, 2010, 31(11): 3656-3660.
LIN Hang, CAO Ping, LI Jiangteng, et al. Deformation stability of three dimensional slope based on Hoek-Brown criterion, Rock and Soil Mechanics, 2010, 31(11): 3656-3660.
[10] 林杭, 曹平, 赵延林, 等. 强度折减法在Hoek-Brown准则中的应用[J]. 中南大学学报: 自然科学版, 2007, 38(6): 1219-1224.
LIN Hang, CAO Ping, ZHAO Yanlin, et al. The application of strength reduction method in Hoek-Brown criterion[J]. Journal of Central South University: Science and Technology, 2007, 38(6): 1219-1224.
[11] 郑宏, 田斌, 刘德富. 关于有限元边坡稳定性分析中安全系数的定义问题[J]. 岩石力学与工程学报, 2005, 24(13): 2225-2230.
ZHENG Hong, TIAN Bin, LIU Defu. On definition of safety factor of slope stability analysis with finite element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(13): 2225-2230.
[12] 郑颖人, 赵尚毅. 边(滑)坡工程设计中安全系数的讨论[J]. 岩石力学与工程学报, 2006, 25(9): 1937-1940.
ZHENG Yingren, ZHAO Shangyi. Discussion on safety factors of slope and landslide engineering, design[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(9): 1937-1940.
[13] Zhu D Y, Lee C F, Jiang H D. Generalized framework of limit equilibrium methods for slope stability analysis[J]. Geotechnique, 2003, 53(4): 377-395.
[14] 曹平, 张科, 汪亦显, 等. 复杂边坡滑动面确定的联合搜索法[J]. 岩石力学与工程学报, 2010, 29(4): 814-821.
CAO Ping, ZHANG Ke, WANG Yixian, et al. Mixed search algorithm of critical slip surface of complex slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(4): 814-821.
[15] Priest S D. Determination of shear strength and three-dimensional yield strength for the Hoek-Brown criterion[J]. Rock Mech Rock Engng, 2005, 38(4): 299-327.
[16] 沈银斌, 朱大勇, 姚华彦. 基于广义Hoek-Brown 破坏准则的边坡临界滑动场[J]. 岩石力学与工程学报, 2011, 30(11): 2267-2275.
SHEN Yinbin, ZHU Dayong, YAO Huayan. Critical slip field of slope based on generalized Hoek-Brown failure criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(11): 2267-2275.
(编辑 何运斌)
收稿日期：2012-05-07；修回日期：2012-09-11
基金项目：国家自然科学基金资助项目(50878212)，四川省科技计划项目(2013JY0119)
通信作者：吴启红(1981-)，男，四川乐至人，博士，副教授，从事岩土工程及地质工程的研究和教学；电话：18628066800；E-mail:wqh1016@126.com
