J. Cent. South Univ. (2012) 19: 1530-1536
DOI: 10.1007/s11771-012-1172-5
Dynamic analysis and simulation of four-axis forced synchronizing banana vibrating screen of variable linear trajectory
LIU Chu-sheng(刘初升), ZHANG Shi-min(张士民), ZHOU Hai-pei(周海沛), LI Jun(李珺),
XIA Yun-fei(夏云飞), PENG Li-ping(彭利平), WANG Hong(王宏)
School of Mechanical and Electrical Engineering, China University of Mining and Technology, Xuzhou 221008, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: A new concept of banana vibrating screen which has the same effect as traditional banana vibrating screen in a new way was put forward. The dynamic model of vibrating screen was established and its working principle was analyzed when the action line of the exciting force did not act through the centroid of screen box. Moreover, the dynamic differential equations of centroid and screen surface were obtained. The motions of centroid and screen surface were simulated with actual parameters of the design example in Matlab/Simulink. The results show that not only the amplitude has a significant decrease from 9.38 to 4.10 mm, but also the throwing index and vibrating direction angle have a significant decrease from 10.49 to 4.59, and from 58.10° to 33.29°, respectively, along the screen surface, which indicates that motion characteristics of vibrating screen are consistent with those of traditional banana vibrating screen only by means of a single angle of screen surface. What’s more, such banana vibrating screen of variable linear trajectory with greater processing capacity could be obtained by adjusting the relative position of force center and the centroid of screen box properly.
Key words: four-axis; banana vibrating screen; forced synchronizing; variable linear trajectory; dynamics; simulation
1 Introduction
Linear vibrating screen is also called two-axis inertia vibrating screen, which mainly consists of the screen box, the base and the vibration generator (or vibration motor) [1]. When the action line of the exciting force excited by the vibration generator (or vibration motor) acts through the centroid of screen box, the whole screen box produces a translational motion, which means that any point on the screen box has the same motion trajectory as the centroid. Conversely, if the action line of the exciting force deviates from the centroid of screen box, complex variable linear motions will be achieved with the velocity, throwing index and vibrating direction angle, changing gradually the points on the screen box and providing an ideal motion for the screen surface [2-3].
The earliest research on vibrating screen of variable trajectory started in the late 20th century in China, which was mainly about drilling fluid. Most of these early studies were focused on single-axis vibrating screen of variable elliptical trajectory or two-axis vibrating screen of variable linear trajectory, whereas, multi-axis vibrating screen was seldom mentioned. In this work, a systematic study of representations of vibrating screen of variable linear trajectory was carried out.
HOU et al [4] studied intensively on the characteristics of vibrating screen of variable linear trajectory and concluded that complex motion trajectory of linear vibrating screen could be obtained without any geometrical constraint based on this principle. With increasing concentration of vibrating screen of variable linear trajectory, YU et al [5] established a more complete model of screen box while the action line of the exciting force deviated from the centroid of screen box and specified again the characteristics of the vibrating screen of variable linear trajectory in detail.
It can be learned that the vibrating screen of variable linear trajectory optimizes the vibration parameters of screen box to a certain degree, making the distribution of sieving material well-distributed and providing an ideal sieving method for greater processing capacity and higher efficiency.
In 1970s, banana vibrating screen was firstly applied in metallurgical industry in France, which was proved to be a sieving method for greater processing capacity and higher efficiency after industrial application. In fact, the banana vibrating screen was consistent with vibrating screen of variable trajectory in nature [6]. How to find the combination of them and apply it to industrial application is the purpose of this work. Through analysis and comparison, it can be found that it is possible to reach the same purpose through vibrating screen of variable linear trajectory [7-10].
Aiming at developing a new type of banana vibrating screen with both high efficiency and simple structure, four-axis forced synchronizing banana vibrating screen of variable linear trajectory has been put forward and its dynamic problems has been analyzed in this work.
2 Dynamic characteristic analysis
As shown in Fig. 1, this vibrating screen has two linear exciters, each of which consists of two axes. The action line of exciting force by the right exciter has an included angle of δ with x-axis and acts through point O, the centroid of screen box, while the action line of exciting force by the left exciter has an included angle of β with y-axis and acts through point O1 which has a horizontal distance of L from point O.
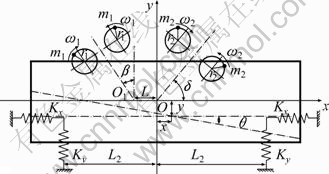
Fig. 1 Mechanical model of vibrating screen
According to the mechanical model of vibrating screen in Fig. 1, the dynamic differential equations of the centroid has been obtained after ignoring damping forces in the system:
 (1)
(1)
where M is the vibrating mass (kg); m1 is the eccentric block mass of the left linear exciter (kg); m2 is the eccentric block mass of the right linear exciter (kg); J is the rotational inertia of M to the centroid of the screen box (kg·m2); x is the displacement in the x-axis direction (m); y is the displacement in the y-axis direction (m);  is the acceleration in the x-axis direction (m/s2); ? is the acceleration in the y-axis direction (m/s2); Kx is the spring stiffness in the x-axis direction (N/m); Ky is the spring stiffness in the y-axis direction (N/m); r1 is the eccentric block radius of the left linear exciter (m); r2 is the eccentric block radius of the right linear exciter (m); ω1 is the driving frequency of the left linear exciter (rad/s); ω2 is the driving frequency of the right linear exciter (rad/s), moreover, ω1=ω2=ω; L1 is the horizontal distance between the left isolation spring and the centroid of the screen box (m); L2 is the horizontal distance between the right isolation spring and the centroid of the screen box (m); L is the horizontal distance between point O1 and point O (m); β is the angle between the action line of the exciting force and y-axis excited by the left exciter (°); δ is the angle between the action line of the exciting force and x-axis excited by the right exciter (°); θ is the rotational angle of the screen box (°);
is the acceleration in the x-axis direction (m/s2); ? is the acceleration in the y-axis direction (m/s2); Kx is the spring stiffness in the x-axis direction (N/m); Ky is the spring stiffness in the y-axis direction (N/m); r1 is the eccentric block radius of the left linear exciter (m); r2 is the eccentric block radius of the right linear exciter (m); ω1 is the driving frequency of the left linear exciter (rad/s); ω2 is the driving frequency of the right linear exciter (rad/s), moreover, ω1=ω2=ω; L1 is the horizontal distance between the left isolation spring and the centroid of the screen box (m); L2 is the horizontal distance between the right isolation spring and the centroid of the screen box (m); L is the horizontal distance between point O1 and point O (m); β is the angle between the action line of the exciting force and y-axis excited by the left exciter (°); δ is the angle between the action line of the exciting force and x-axis excited by the right exciter (°); θ is the rotational angle of the screen box (°);  is the rotational angle acceleration of the screen box (°); α1 is the starting phase angle of m1 (°); α2 is the starting phase angle of m2 (°).
is the rotational angle acceleration of the screen box (°); α1 is the starting phase angle of m1 (°); α2 is the starting phase angle of m2 (°).
In order to study the law of vibrating screen further, let the starting phase angles be zero after all axes are fixed following the requirements of design, and then get the form of steady-state solutions of forced vibration based on the vibration theory of multi-degree of freedom system [11-13], which can be expressed as
 (2)
(2)
Substituting Eq. (2) into Eq. (1), we obtain:
 (3)
(3)
where
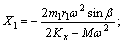
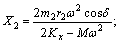
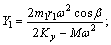
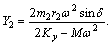
Eventually, we get the steady-state solutions of x, y and θ. Therefore, the motion of centroid of screen box can be expressed as
 (4)
(4)
Therefore, it can be stated from Eq. (4) that the motion of centroid of screen box is a straight line, while the motion of the point on the screen box is a synthetic motion of the linear motion and the swinging motion relative to the centroid of screen box.
3 Theoretical analysis of arbitrary point motion on screen box
First, a rectangular coordinate system with the centroid of screen box is set as the origin of coordinates, then the coordinates of arbitrary point D on the screen box are set as (Dx, Dy), finally, the motion equations are obtained:
 (5)
(5)
Eliminating t, we obtain:
 (6)
(6)
The results shown above suggest that the motion trajectory of arbitrary point on the screen box is a straight line. Meanwhile, the slope of the straight line is the tangent of the vibrating direction angle γ, which is defined as
 (7)
(7)
Thus, the conclusion is drawn that the motion trajectory of arbitrary point on the screen box is a straight line. Furthermore, the length and direction of the linear motion trajectory show a regular change with the position changes of the point on screen box. Additionally, reasonable transporting and throwing velocity can be obtained by adjusting the positions, vibration intensities and directions of the linear exciters.
4 Motion characteristic analysis and simulation
4.1 Motion characteristic analysis of centroid of screen box
For further understanding the motion characteristics of vibrating screen, the motion of centroid of screen box was simulated by means of Matlab/Simulink with parameters of the design example, as shown in Fig. 2.

Fig. 2 Preliminary model of design example
Substituting parameters (see Table 1) into the simulation-compute model of Eq. (1), as shown in Fig. 3, we get the motion time course for signals of displacement, velocity and acceleration of the centroid of screen box in directions of x-axis, y-axis and θ after the vibration is stable.
Figure 4 illustrates that in the x-axis direction, the displacement, velocity and acceleration have an amplitude of 0.006 m, 0.20 m/s and 10 m/s2, respectively, with the time of peak-peak being 0.06 s. Compared with parameters in x-axis direction, the amplitude of displacement and velocity have a small increase correspondingly in the y-axis direction, whereas acceleration amplitude almost doubles that in the x-axis direction and the peak-peak time remains the same; In the direction of θ, it is clear that the screen box has a maximum swing of about 0.003 5 rad, while the amplitudes of velocity and angle acceleration are 0.15 rad/s, 7.5 rad/s2, respectively, and the peak-peak time is still about 0.06 s.
The periodic signals above essentially reflect the integrated information of exciting frequency of system and natural frequency in the three-DOF system. Detailed analysis requires frequency spectrum analysis of signals, implemented by fast Fourier transform (FFT), as shown in Fig. 5.
Figure 6 shows the results for an excitation frequency of about 17 Hz. It can be known that the natural frequency of about 3 Hz in the x-axis direction is lower than that in directions of y and θ, which is caused by its stiffness.
Table 1 Dynamic parameters of vibrating screen

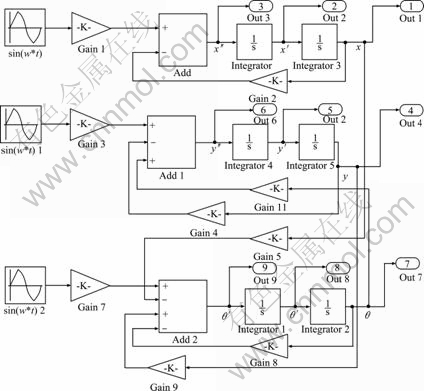
Fig. 3 Simulation-compute model of centroid of screen box
Fig. 4 Motion time course for signals of centroid of screen box: (a1)-(a3) Translational properties of screen box in x-axis; (b1)-(b3) Translational properties of screen box in y-axis; (c1)-(c3) Rotational properties of screen box
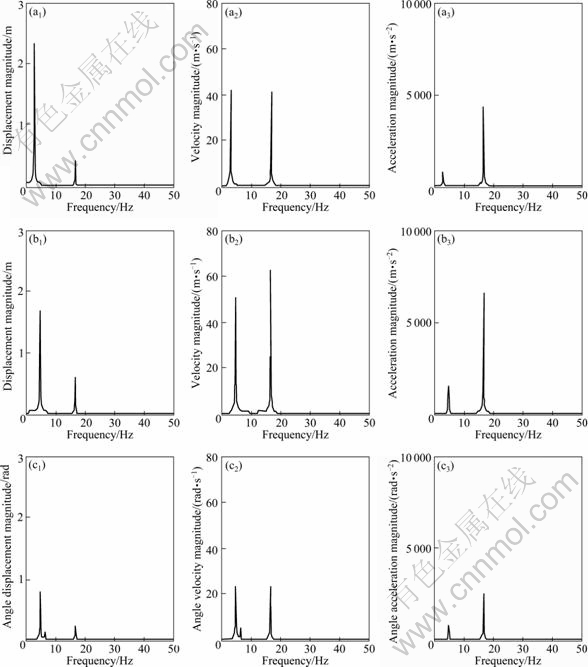
Fig. 5 Frequency spectrum analysis for signals of centroid of screen box in accordance with Fig. 4: (a1)-(a3) Translational properties of screen box in x-axis; (b1)-(b3) Translational properties of screen box in y-axis; (c1)-(c3) Rotational properties of screen box
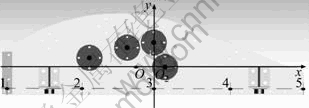
Fig. 6 Locations of five points on screen surface
4.2 Motion characteristic analysis of arbitrary point on screen box
According to the simulation-compute model of centroid of screen box, we can learn the motion characteristics of arbitrary point on the screen box comprehensively. However, for the motion of materials, what we need to know is the motion characteristics of the points on screen surface. So, five points have been chosen along the screen surface (current position of the red line) orderly, as shown in Fig. 6.
For this purpose, the rectangular coordinate system has been constructed with the mid-point of screen surface O2 as the origin of coordinates and the surface where the centroid O is located as the x-axis, and the parameters of five points are listed in Table 2.
Putting the parameters (see Table 2) into the simulation-compute models, as shown in Figs. 7 and 8, we obtain the vibration parameters of five points, such as velocity, vibration amplitude and vibrating direction angle, as listed in Table 3.
It can be seen from Table 3 that in the process from feeding end to delivery end, the horizontal speed keeps invariant, whereas, the amplitude, the vertical velocity, the throwing index and the vibrating direction angle significantly decrease respectively [8,14]. That is the ideal motion form for the screen surface. Because there are more materials at the feeding end and less material at the delivery end, more powerful throwing intensity and large vibrating direction angle should be provided for the feeding end to make sure that materials have a better stratifying and discharging “environment” [15]. On the contrary, the delivery end should be provided with weak throwing intensity and small vibrating direction angle ensuring materials stay a long time on the screen surface to discharge materials fully.
Table 2 Location parameters of five points on screen surface

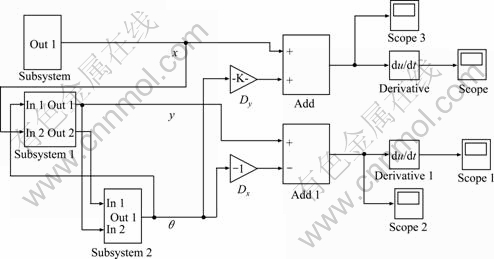
Fig. 7 Simulation-compute model of displacement and velocity of five points
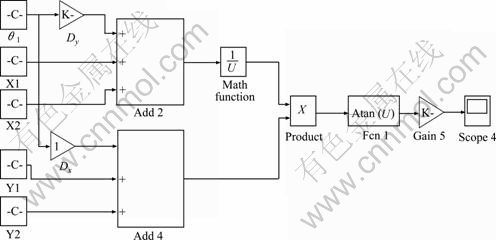
Fig. 8 Simulation-compute model of vibrating direction angle γ of five points
Table 3 Vibration parameters of five points on screen surface

Figure 9 shows the trajectory graph [16-18] of five points on the screen surface based on the vibration parameters in Table 3.
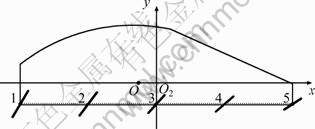
Fig. 9 Trajectory graph of five points on screen surface
In conclusion, it can be stated that the screening characteristics of this vibrating screen are in accordance with those of the banana vibrating screen.
5 Conclusions
1) On the basis of banana screening principle, a new type of banana vibrating screen of variable linear trajectory has been presented, avoiding the difficult machining process of traditional banana vibrating screen and providing a screening method that could be used for references for higher efficiency.
2) The mode of forced synchronizing has been adopted to make sure that two axes in the middle operate synchronistically by two gears. Meanwhile, each of the two axes operates with another axis providing a new way for multi-axis synchronization.
3) The motion characteristics have been obtained of the centroid and points on the screen surface based on Matlab/Simulink. As a result of the simulation, it can be concluded that the screening characteristics of this vibrating screen are in accordance with those of the banana vibrating screen and it is a way of improving screening efficiency effectively.
4) The exciting forces of the linear exciters, the directions and locations of the linear exciters are the key factors to the screening efficiency. The vibrating screen with greater processing capacity could be obtained by adjusting the relative position of the center of force and the centroid of the screen box properly.
References
[1] YAN Feng. Screening machine [M]. Beijing: China Coal Industry Publishing House, 1995: 46-52. (in Chinese)
[2] HOU Yong-jun, LI Guo-zhong, LIU Hong-bin, ZHANG Ming-hong. Working principle and simulation of variable linear shaker [J]. Oil Field Equipment, 2003, 32 (5): 17-19. (in Chinese)
[3] COURTNEY D. Novel screening unit provides alternative to conventional shale shaker [J]. Oil & Cas Journal, l999, 97(15): 40-48.
[4] HOU Yong-jun, LI Guo-zhong, LIU Hong-bin, ZHANG Ming-hong. Working principle and simulation of variable linear shaker [J]. Oil Field Equipment, 2003, 32(5): 17-19. (in Chinese)
[5] YU Jing-ge, DONG Huai-rong, AN Qing-bao. Shale shaker kinetics analysis while the resulting exciting forces drifting off the screening box centroid [J]. Petrol Eum Drilling Techniques, 2009, 37(4): 76-79. (in Chinese)
[6] GUO Nian-qin, LOU Hong-min, HUANG Wei-ping. Design and research on the new combining vibrating screen [J]. Advanced Materials Research, 2011, 201/202/203: 504-509.
[7] WEN Bang-chun, LI Yi-nong, ZHAGN Yi-min, SONG Zhan-wei. Vibratory utilization engineering [M]. Beijing: Science Press, 2005: 61-67. (in Chinese)
[8] HE Xiao-mei, LIU Chu-sheng, ZHANG Cheng-yong. Optimal design of large vibrating screen based on multiple frequencies constraints and analytical sensitivity methods [J]. Journal of Central South University: Science and Technology, 2011, 42(3): 664-670. (in Chinese)
[9] ZHAO Yue-min, LIU Chu-sheng, HE Xiao-mei, ZHANG Cheng- yong, WANG Yi-bin, REN Zi-ting. Dynamic design theory and application of large vibrating screen [J]. Procedia Earth and Planetary Science, 2009, 1(1): 776-784.
[10] WEN Bang-chun, LIU Feng-qiao. The working theory and applications of vibrating machinery [M]. Beijing: China Machine Press, 1982: 5-16. (in Chinese)
[11] VOLKER W, MATTHIAS S, HEIMO G. Working with characteristic curves for the optimization of sizing on circular vibrating screens [J]. Mineral Processing, 2007, 48(7): 14-29.
[12] PAL T G, SCHMIDTBERT R A. Combining analytical and experimental modal analysis for effective structural dynamic modeling [C]// Proceedings of the International Modal Analysis Conference & Exhibit. Orlando: Union Coll, 1982: 265-271.
[13] SONG Yan, JIANG Xiao-hong, SONG Juan, ZHANG Jian-xun. Dynamic analysis of a chaotic vibrating screen [J]. Procedia Earth and Planetary Science, 2009, 1(1): 1525-1531.
[14] ZHAO La-la, LIU Chu-sheng, YAN Jun-xia. A virtual experiment showing single particle motion on a linearly vibrating screen-deck [J]. Mining Science and Technology (China), 2010, 20(2): 276-280.
[15] GU Qing-bao, ZHANG En-guang. Study on complex-locus vibrating screen [J]. Ming & Processing Equipment, 1998: 42-44. (in Chinese)
[16] PDDER M. The Mogensen e-series-a new screening concept [J]. Aufbereitungs Technik, 1996, 7(37): 311-315.
[17] HE Xiao-mei, LIU Chu-sheng. Dynamics and screening characteristics of a vibrating screen with variable elliptical trace [J]. Mining Science and Technology, 2009: 508-513.
[18] WEN Bang-chun. Synchronization theory of self-synchronous vibrating machines with ellipse motion locus [C]// Proceedings of ASME Vibrating and Noise Conference. Boston: American Society of Mechanical Engineers, 1987: 495-500.
(Edited by DENG Lü-xiang)
Foundation item: Projects(50574091, 50774084) supported by the National Natural Science Foundation of China; Project(50921001) supported by the Innovative Research Group Science Foundation, China; Project supported by Jiangsu Scientific Researching Fund Project (“333” Project), China
Received date: 2011-05-17; Accepted date: 2011-12-12
Corresponding author: LIU Chu-sheng, Professor, PhD; Tel: +86-15365893035; E-mail: trueman2008@163.com