Micromagnetic simulation and experimental study on microwave permeability of nano-magnetic films

DENG Lian-wen(邓联文), HUANG Xiao-zhong(黄小忠), ZHOU Ke-sheng(周克省), YANG Bing-chu(杨兵初)

School of Physics Science and Technology, Central South University, Changsha 410083, China

Received 15 July 2007; accepted 10 September 2007

Abstract: From the point of view of application in the microwave band, the theoretic and experimental researches of nanostructural magnetic films were carried out. Micromagnetic structure of the nano-magnetic film was simulated by the finite element method. The typical micromagnetic was obtained. Corresponding experiments were also done aiming at the Co₄₀Fe₄₀B₂₀-SiO₂ nano-granular films. The results show that the characteristics of nano-magnetic film correspond with the micromagnetic ripple theory. The microwave permeability of nano-magnetic films deduces and well fits the Landau-Lifshitz-Gilbert (LLG) equation. The films present large microwave permeability and high resonant frequency (μ′ and μ″ at 2 GHz are about 100 and 40 respectively and the resonant frequency is about 2.8 GHz). The additional peak of μ″ originated from perpendicular anisotropy and micromagnetic ripple structure can be suppressed by the annealing process. Thus, the microwave complex permeability spectra of these nano-magnetic films can be tailored for different applications.

Key words: nano-granular film; random anisotropy model; micromagnetic simulation; ripple structure; microwave permeability

1 Introduction

The random anisotropy theory, which was used to explain the origin of the high permeability of the amorphous soft magnetic materials, is now widely used in various objects such as nanocrystalline soft magnetic materials [1], nanomagnetic granular films [2]. But numerical simulation method based on this theory for exploring magnetic problems was little reported. BERKOV et al[3] computed the magnetization process through a two-dimension hexagonal lattices model, and the typical micro-magnetic ripple structure [3] was gotten. ARANDA et al[4] and CHECHENIN[5] calculated the transverse biased initial susceptibility of the nanomagnetic film, but did not present the micromagnetic structure. These thin films are composites consisting of ferromagnetic metallic particles randomly embedded in dielectric matrix. The ferromagnetic particles in the composites are several nanometers in diameter and separated from each other by insulative barriers. Electromagnetic performances of the granular films can be tailored by adjusting particle size, volume fraction and other structural parameters. Much attention is paid to granular films for their unique performances [6]. Based on the random anisotropy theory, micromagnetic structure and microwave permeability of magnetic films were studied in this work. Furthermore, some experimental research on Co₄₀Fe₄₀B₂₀SiO₂ nano-granular films were carried out to validate the calculated results.

2 Micromagnetics model and simulation

The numerical simulation of the magnetic material is based on the spin of each lattice. The net spin of the lattice is the magnetization of the sample. And the magnetodynamics of each spin is described by the Landau-Lifshitz-Gilbert (LLG) equation:

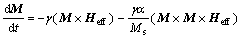       (1)

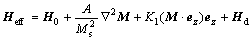      (2)

where  M is magnetization vector; t is time; α is phenomenological damping parameter; γ is gyromagnetic ratio; M_s is saturation magnetization. H_eff is effective magnetic field; H_o is external magnetic field; H_d is demagnetization field; A is exchange constant; K₁ is first-order magnetocrystalline anisotropy constant, and e_z is unit vector of the easy axis.

The LLG equation is a nonlinear differential equation, and in general is solved numerically.

In this work the software of GNU codes Magpar [7] was adopted.

The discussed model in this work was a strip film, with the dimension of 1 000 nm×5 000 nm×15 nm. Then it was divided into 22 079 tetrahedral finite elements. And the average length of the tetrahedral in the film plane was 30 nm, which was considered a characteristic diameter of nano-granular of films. In the model, each finite element was considered magnetic material that had the identical exchange constant, the damping constant, saturation magnetization of 2 T, magnetocrystalline anisotropy of 20 kA/m, but a random easy axis. So the film has the random anisotropy. But this film is finite, the magnetocrystalline anisotropy of the edge of the film was set to 2 MA/m and the easy axis was set to y-axis to neglect the effect of the demagnetization energy in the edge of the film. Therefore, the magnetization direction was supposed to be y-axis, and the magnetic structure of the total film was nearly a single domain. For the sake of adjusting the size of the granular, the scale of the initial model was changed instead of building a new model and dividing the mesh again. For example, when the size of the model reduced by 5 times, the diameter changed to 6 nm and the dimension changed to 200 nm×1 000 nm×3 nm.

When the exchange constant was 1.0×10^-11, the magnetic dispersion angle of different granular sizes is shown in Fig.1, and it increases linearly with the granular size. That is nearly correspondent with the ripple theory. When the exchange constant is 1.0×10^-12, it can be inferred from Fig.1 that the magnetic dispersion angle increases by a quite small slope. Thus, all the system

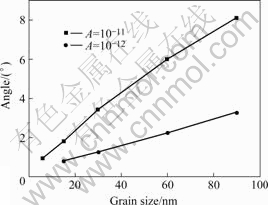
Fig.1 Relationship between magnetic dispersion angle and granular size at different exchange constants

shows the typical magnetic ripple structure as a result of the magnetostatic interaction caused by the exchange interaction and the random anisotropy interaction. When the granular diameter increases, the coupling region hardly changes, which implies that the wavelength of the ripple structure does not change and is still in the linear scope of the ripple theory. When the granular diameter increases and exceeds the exchange length, the wavelength increases. A quite wide coupling region still forms, and the reason is probably the effect of magnetostatic interaction.

When constant magnetic anisotropy field H_k of 5 kA/m is in x-axis, the film possesses magnetic anisotropy. According to distribution of volume of the tetrahedral finite elements, the magnetic anisotropy field of 5 621 kA/m is determined by the geometry configuration. Damping factor was set to be 0.02 in the permeability calculation of nano-granular films. The microwave complex permeability of the nano-granular film with granular diameter of 15 nm is shown in Fig.2. It is obvious that, besides a main peak near 5 GHz, there is an additional peak of μ″ at nearly 8.7 GHz. Further calculation results prove that the additional peak is not the contribution of the random anisotropy. This phenomenon is actually resulted from the perpendicular anisotropy and magnetic ripple effect [8-9]. The real part of permeability maintains large value of 100 below 5 GHz. These calculated results show that the nano-granular films possess good magnetic characteristics in the high frequency range.

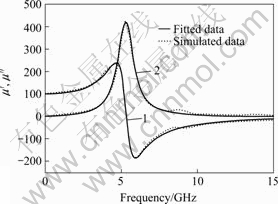
Fig.2 Calculated complex permeability spectra of film with granular size of 15 nm: 1—μ′; 2—μ″

3 Experimental and discussion

(Co₄₀Fe₄₀B₂₀)_1-x-(SiO₂)_x granular films were deposited on glass substrates by RF magnetron sputtering and Co₄₀Fe₄₀B₂₀ composite target containing SiO₂ chips was used. Volume fraction (φ) of SiO₂ was controlled by the total area of chips. Sputter pressure was 0.665 Pa and sputter power was set at 200 W. An array of magnets providing 40 mT in-plane field was used to induce in-plane anisotropy in the films. The substrates were cooled by circulating water. Some of the deposited films were annealed at 250-400 ℃ for 30-90 min in a vacuum of 2.66×10^-4 Pa without magnetic field, then cooled to room temperature. The morphology was analyzed by scanning probe microscopy (SPM). Complex permeability in the frequency range of 0.5-5 GHz was measured by the microstrip method with vector network analyzer.

Fig.3 shows the SPM morphology of (Co₄₀Fe₄₀B₂₀)_0.8(SiO₂)_0.2 nano-granular film. It shows that the deposited film is morphologically uniform and SiO₂ wrapps the alloy particles and forms the insulative meshwork matrix. It is clearly shown that the alloy particles are isolated from each other and embedded in the SiO₂ matrix. The particle size is about 10 nm.

Fig.3 Morphology of (Co₄₀Fe₄₀B₂₀)_0.8-(SiO₂)_0.2 nano-granular film

Complex permeability in 0.5-5 GHz for (Co₄₀Fe₄₀B₂₀)_0.8-(SiO₂)_0.2 nanogranular films was measured, as shown in Fig.4. μ′ and μ″ at 2 GHz are about 100 and 40 respectively, and the resonant frequency is about 2.8 GHz with an additional peak of μ″ at 4.5 GHz. The nano-granular film possesses not only relatively large saturation magnetization but also high resistivity, which can suppress the macroscopical eddy current effect. Furthermore, the strengthened interaction between magnetic particles in nanometer size makes the rotation magnetization process more easily. Thus, the film presents good soft magnetic capability and high permeability. According to the Snoek formula, saturation magnetization of (Co₄₀Fe₄₀B₂₀)_0.8-(SiO₂)_0.2 nanogranular films is smaller than that of the calculated film in the model. So the resonant frequency of the experimental film is much lower.

As for the additional peak, a model was proposed to account for the behavior of the high-frequency response of samples with weak stripe structure [10-11]. By supposing that the sample can be divided into two sets of

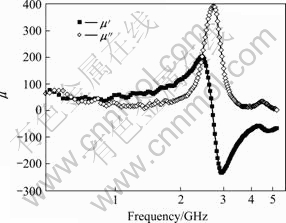
Fig.4 Complex permeability spectra of deposited granular film

stripes, the magnetization is homogeneous within each set of stripe. This is shown using the Smit and Beljers method, where at least two resonance modes can be observed. The expressions of the resonance frequency and the permeability are derived. It can be shown that for the fundamental mode excited by a microwave field along the hard axis, the precession of the magnetization is in phase in both sets of stripes. The presence of higher-order peaks on the permeability along the hard axis is attributed to spin wave resonance. A microwave field parallel to the easy axis excites a mode, where the precession of the magnetization has opposite sign in the two sets of stripes.

The sputter-deposited films are generally under residual stress. This residual stress, once relieved by modest annealing, becomes a driving force to change the microstructure and improves the magnetic properties. In general, the microstructural evolution associated with postdepostion annealing includes defect healing, nucleation and grain growth. The complex permeability in 0.5-5 GHz for the  (Co₄₀Fe₄₀B₂₀)_0.8-(SiO₂)_0.2 film annealed under the conditions of 350 ℃, 60 min is shown in Fig.5. It is obvious that the resonant frequency is near 2.5 GHz and the additional peak disappears. The properties of the spectra are fairly conventional as shown by microwave permeability recorded along the hard axis. It can be explained by the classical Landau-Lifschitz approach for saturated thin films with in-plane uniaxial anisotropy. Thus, the perpendicular anisotropy that is correlated with the presence of micromagnetic ripple structure and stripe domains is suppressed after annealing. The local anisotropy and inharmonies originated from impurities, defects or inconsistent orientation of atoms, are eliminated gradually during the microstructural evolution in the annealing process.

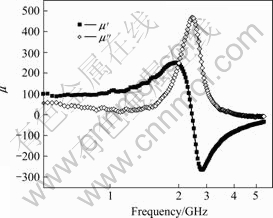
Fig.5 Complex permeability spectra of granular film after annealing

4 Conclusions

1) Micromagnetic structure of the nanomagnetic film can be simulated by the finite element method. The typical micromagnetic ripple structure is obtained and its characteristic is demonstrated to correspond with the micromagnetic ripple theory. Furthermore, the microwave permeability of nanomagnetic film with ripple structure is calculated according to the LLG equation.

2) Co₄₀Fe₄₀B₂₀-SiO₂ nano-granular films may be synthesized by RF magnetron sputtering and composite target.

3) Results from the calculation and experiments all prove that the films consisting of nano-granular particles present large microwave permeability and high resonant frequency. μ′ and μ″ at 2 GHz are about 100 and 40 respectively and the resonant frequency is about 2.8 GHz. The additional peak originated from perpendicular anisotropy and micromagnetic ripple structure can be suppressed by the annealing process.

[1] YAMAUCHI K, YOSHIZAWA Y. Recent development of namocrystalline soft magnetic alloys [J]. Nanostructured Mater, 1995, 6(2): 247-251.

[2] OHNUMA S, FUJIMORI H, MASUMOTO T, XIONG X Y, PING D H, HONO K. FeCo-Zr-O nanogranular soft-magnetic thin films with a high magnetic flux density [J]. Appl Phys Lett, 2003, 82(1): 946-949.

[3] BERKOV D V, GORN N L. Quasistatic remagnetization processes in two-dimensional systems with random on-site anisotropy and dipolar interaction: Numerical simulations [J]. Phys Rev B, 1998, 57(2): 14332-14335.

[4] ARANDA G R, CHUBYKALO O A, GONZ?LEZ J, GONZALEZ J M, LENGSFIELD B. Micromagnetic simulation of transverse biased initial susceptibility measurements [J]. Physica B, 2001, 299(1): 205-207.

[5] CHECHENIN N G. Micromagnetism and high-frequency properites of soft magnetic films[J]. J Magn Magn Mat, 2006, 300(1): 198-202.

[6] IKEDA K, KOBAYASHI K, FUJIMOTO M. Microstructure and magnetic properties of (Co-Fe)-Al-O thin films [J]. J Am Ceram Soc, 2002, 85(1): 169-173.

[7] SCHOLZ W, FIDLER J, SCHREFL T, SUESS D, DITTRICH R, FORSTER H, TSIANTOS V. Scalable parallel micromagnetic solvers for magnetic nanostructures[J]. Comp Mat Sci, 2003, 28(1): 366-369.

[8] SURAN G, NAILI M, NIEDOBA H, MACHIZAUD F, ACHER O, PAIN D. Magnetic and structural properties of Co-rich CoFeZr amorphous thin films [J]. J Magn Magn Mat, 1999, 192(1): 443-446.

[9] HARTE K J. Theory of large-angle ripple in magnetic films [J]. J Appl Phys, 1966, 37(2): 1295-1298.

[10] ACHER O, BOSCHER C, BRULE B, PERRIN G, VOUKADINOVIC N, SURAN G, JOISTEN H. Microwave permeability of ferromagnetic thin films with stripe domain structure [J]. J Appl Phys, 1997, 81(11): 4057-4059.

[11] CHAPPERT C, BEAUVILLAIN P. Ferromagnetic resonance studies of very thin cobalt films on a gold substrate [J]. Phys Rev B, 1986, 34(8): 3192-3194.

(Edited by CHEN Can-hua)

Foundation item: Project (60771028) supported by the National Natural Science Foundation of China

Corresponding author: DENG Lian-wen; Tel: +86-27-8836424; E-mail: dlw626@163.com