Modeling of shear induced coarsening effects in semi-solid alloys

M. MODIGELL¹, A. POLA²

1. AVT, Chair of Mechanical Process Engineering, RWTH Aachen University,

Turmstr. 46, D 52056 Aachen, Germany;

2. Dipartimento di Ingegneria Meccanica e Industriale, Uni. degli Studi di Brescia,

via Branze 38, 25123 Brescia, Italy

Received 13 May 2010; accepted 25 June 2010

Abstract: In long-term rheological shear experiments with semi-solid alloys, coarsening of the particles will falsify the interpretation of the experimental results. The coarsening is intensified by the shear induced convection and the mean size of the particles is changed significantly during the experiments. A simple model has been set up which takes the influence of the convection into account. The resulting growth law has been simplified for diffusion and convection dominated growth. The growth law was verified with shear experiments in a Searl-rheometer with A356 and tin-lead alloys. The experiments demonstrated that under convection the growth follows a linear time law and that the rate constant depends on the root of the shear rate. The correction of experimental results to gain the true viscosity function is demonstrated for a shear jump experiment with A356.

Key words: microstructure; coarsening; Ostwald ripening; flow function; viscosity; rheology; semi-solid alloys

1 Introduction

Growth and coarsening of particles in semi-solid alloys, or Ostwald ripening, are the essential processes to prepare a material which has suitable properties for processing. Depending on the process route, the coarsening is performed in the material under rest or under shear condition. In the past decades, numerous theoretical and experimental investigations have been published focused on the coarsening in resting semi-solid material. It has been verified that for diluted systems and those under diffusionally controlled and isothermal conditions, the cubic relation for the growth of particles, which has been developed by LIFSHITZ and SLYOZOW[1] and WAGNER[2] (LSW-theory), is valid:

                             (1)

where d is the mean particle diameter at time t, d₀ is the diameter at the reference time t=0 and K_LSW is the  growth constant, depending on the temperature and physical-chemical parameters of the system. Although the published values for the growth constant show some scattering[3], the calculation of the growth of particles in conventional alloys is possible with reasonable accuracy. Contrary to that, publications about coarsening under shear conditions are rare. There is no generally accepted law of growth comparable to Eq.(1) and there is lack of systematic investigations under well defined conditions. Hence, it is not possible to forecast the growth of particles under shearing although the size of the particles influences the forming-process as well as the mechanical properties of the produced parts.

It has been pointed out that coarsening of particles will happen during shear experiments which are performed to investigate the flow properties of semi-solid alloys[4]. The coarsening affects the evaluation of the experimental data which results in an apparent shear-thinning or shear thickening behaviour of the material depending on the experimental procedure[5]. To unify the experimental data, it is necessary to account for the temporal change of the size of the particles during the experiment. A simple approach has been chosen to set up a growth law which combines diffusion and convection. Experiments have been performed in different rotational rheometers with different alloys, tin-lead and aluminium, to verify the model.


2 Existing theories

The driving force for the coarsening of semi-solid material is the reduction of the free energy stored in the interphase between solid and liquid. Therefore, dendritic particles will become globules and large particles will grow on the cost of small ones. The LWS theory, which models the growing of globular particles, is based on the following assumptions: 1) dilute solution with solid fraction φ_s going to zero, 2) no relative motion between particles and fluid, 3) transport of matter by diffusion only, 4) no contact between particles, and 5) spherical particles.

Generally, the growth law according to Eq.(1) is verified experimentally. Discrepancies are found in the value of the growth constant. One possible reason is that it is difficult to fulfil the second assumption and consequently the third as well. Small differences in density of liquid and solid phase or fluctuations in temperature result in a relative motion between solid and fluid, which affects the mass transfer. Special methods have been applied to prevent that motion, e.g. by fixing the particles with electromagnetic force[6] or by performing the experiment under microgravity condition[7]. The decrease of the growth constant with increasing solid fraction can be explained by the immobilisation of particles in large clusters formed at higher solid fraction. Growth constants in the range of 10^-16-10^{-15 m3}/s have been published[3, 6-7].

In systems where solid and liquid move relatively to each other, convective mass transport in the liquid phase dominates the coarsening of particles and the influence of diffusion is limited on small boundary layers around the surface of the particles. Additional phenomena can influence the gross growing kinetics: breaking of dendrite arms by high shear forces, which produces new nuclei for the formation of larger particles, and collision of particles which results in an increase of particle size. It is difficult to distinguish experimentally between these phenomena. Consequently, the growth laws published in the literature are generally gross laws.

Experimental results indicate an increase of speed of growth under the influence of convection. Because the structure of the flow field which produces the convectional mass transport has not been specified in the literature, a quantitative conclusion cannot be made. AKAIWA et al[8] found in a rotating disc device that for solid fractions below 0.3, the exponent in Eq.(1) changes from 3 to 2.7. At higher solid fractions, the exponent will be 3 but the growth constant is increased compared with the stagnant system. Investigations of RATKE and THIERINGRE[9] results in a second order power law, which would indicate that diffusion is dominant.

The findings of RATKE and THIERINGER have been confirmed by DIEPERS et al[10], who modelled the ripening with the phase-field method. WAN and SAHM[11] have found that in Pb-Sn alloy, the exponent is 3.5 and the growth constant is proportional to the square root of the shear velocity. FAN et al[12] made some interesting observations in a screw extruder which produces very high shear rates and high local turbulence. They found an extreme fast globular growth of primary particles after the nucleation. For the coarsening process, it was found an exponent of more than 8 explained with the narrow size distribution which gives a low driving force for Ostwald ripening.

3 Coarsening in shear rheometer

The coarsening in a Searl rheometer during rheological experiments has been observed by KOKE and MODIGELL[4] and the consequence has been discussed in Ref.[13].

Fig.1 shows the typical course of the viscosity during a simple shear experiment with a tin-lead alloy. The experiment starts with fully liquefied alloy which behaves Newtonian with a very low viscosity. While the melt is sheared with a constant rate, the temperature is decreased. A rapid increase of the viscosity occurs when the precipitation of particles starts. When the temperature has reached the desired level, according to the envisaged solid content, the viscosity reaches a maximum and starts to drop. This decrease is the result of the formation of globules which show a lower hydrodynamic resistance than dendrites, and of coarsening of the particles. The viscosity of the semi-solid material mainly depends on the solid-fraction and the size of the particles. For a suspension of spheres with unique diameter, the viscosity as a function of solid fraction and diameter can be calculated with relation of KRIEGER- DOUGHERTY[14], which has been extended by WINDHAB[15] and QUEMADA[16-17]:

                             (2)

where η_ss and η_l are the viscosity of the semi-solid material and the liquid phase, respectively; φ_s, φ_eff and φ_max are the net, the effective and the maximal volume fraction of particles; d is the particle diameter and δ is the thickness of a stagnant layer of liquid around the particles. It is obvious that the result of a rheological experiment starting when a constant temperature is achieved will be affected by this phenomenon of particle growth.

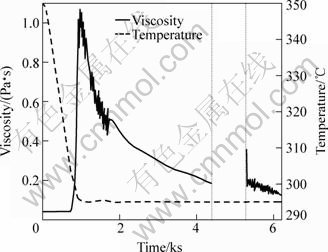
Fig.1 Viscosity and temperature of Sn-15%Pb alloy under shear rate of 100 s^-1 and φ_s of 30%

Fig.2 shows the steady state shear stress functions for two identically prepared samples of tin-lead alloy. The first was measured with ascending order of the shear rate which results in an apparent shear thinning behaviour. The second was performed with descending order of shear rate which results in an apparent shear thickening behaviour. To get the true flow curve, a calibration of the experimental results has to be performed to account for the particle growth.

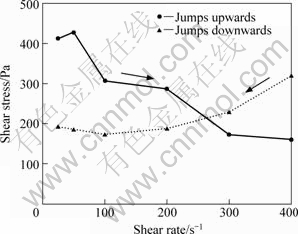
Fig.2 Stress function of Sn-15%Pb for different experimental procedures

Fig.2 demonstrates additionally the difference in growth rate for convective and diffusion coarsening. After constant shearing for around 45 min, the shearing was stopped and the sample was kept in rest for 15 min and then sheared again. After a short overshoot which is the result of the formation of a stable structure during rest, the viscosity will follow exactly the course of the line before the interruption of shearing. It can be concluded that the growing of the particles during the resting time is neglectable compared with that under shear condition.

4 Convective coarsening model

To calculate the coarsening under the influence of convection, a very simple model has been set up which accounts for the flow conditions in the material. The same assumptions are made as in the LSW-theory except for assuming that mass transfer of species which solidify at the particle is influenced by convection. Due to the assumption of low concentrated suspension, coarsening by particle collision should not occur. An additional assumption is that there is no resistance in the crystallization. This means that the rate dominating process is the transport of species in the melt. The flux of material to the particle is expressed with a simple linear transport equation:

                          (3)

where is the mass flux to the particle, m_p is the mass of the particle, k is the mass-transfer coefficient, A is the surface area of the particle and Δφ is the driving potential difference of the transported species between the surface of the particle and the bulk phase of the liquid. The mass transfer coefficient is calculated by using the semi-empirical Sh-relation:

                 (4)

where d is the particle diameter, D is the diffusion coefficient in the liquid, Re and Sc are the dimensionless Reynolds and Schmidt group. The Re and Sc numbers are combined here to give a modified Re-number:

    (5)

The velocity used in the Re-number is here calculated with the shear rate  and the particle diameter d. Combination of Eq.(3) and Eq.(4) and integration gives

(6)

where τ is the dimensionless running time t, t₀ is the reference time according to the reference diameter d₀ and Re₀^*=Re^*(d₀).

The scaling parameter for the time is t^* which is defined by

                            (7)

C is the dimensionless potential difference. Because C is difficult to measure, the rate constant k=C/t^* is defined which has the dimension of a reciprocal time.

Eq.(6) can be simplified for two interesting limiting cases:

When Re₀^*<<4 then

This second power growth law is limited to low contribution of convection to the mass transfer and dominating influence of diffusion. For convective dominated growth, the condition Re₀^*>>4 holds and the simplified growth law is linear in diameter:

                                   (8)

The Sc-number of liquid metals is in the order of 100. The transition from diffusion to convection controlled coarsening should happen for Re-numbers in the order of one, according to the critical modified Re₀^* number of 4.

5 Experiments and results

All experiments have been performed in Searl rheometers, which allows for an almost homogenous and defined shearing of the alloys. The rheometers were equipped with different electrical furnaces to cover in an optimal way the whole temperature range between low melting tin-lead and aluminium alloys. The stability of temperature was 0.1 °C. The measuring systems were made of steel for the tin-lead alloy and graphite for the A356. The rotating roads were grooved evenly to avoid wall slip. To prevent oxidation of the samples, the furnaces have been flushed with pre-heated mixtures of argon and hydrogen.

All samples have been prepared with the procedure explained above. After liquefying the samples were cooled down under constant shearing to the desired temperature in the mushy state; this temperature, corresponding to a proper solid fraction, was previously fixed by means of DSC measurements. This procedure is designed as material preparation. Subsequent step was the shearing period for a definite time to produce convectively coarsened material. After that, the samples were quenched with liquid nitrogen. The sizes of the particles have been determined by metallographic analyses. Experiments were performed with Sn-15%Pb alloy and A356 aluminium alloy, all under comparable conditions. Some rheological experiments have been performed with shear jump test after a defined pre-shearing time to determine the material flow curve.

The influence of the shear rate on the convective coarsening process is clearly demonstrated in Fig.3.

A356 alloy with 48% solid fraction was sheared with two different shear rates during the material preparation as well during the shearing period. At a rate of 200 s^-1, the gradient of the viscosity is much steeper and a stationary viscosity value is reached much earlier than that at 100 s^-1.

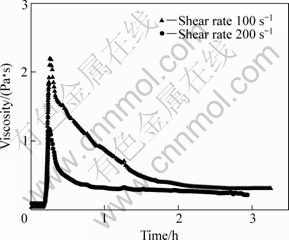
Fig.3 Viscosity during shearing for different shear rates of A356 with φ_s of 40% and constant temperature during shearing period

Fig.4 shows an experiment with A356 where the shear rate during material preparation was 100 s^-1 and was changed to 200 s^-1 for the shearing period, indicated with the vertical line in Fig.4.

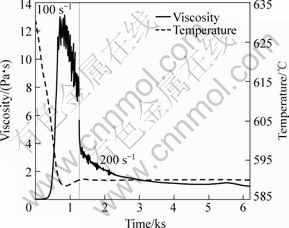
Fig.4 Viscosity curve for A356 with 40% φ_s in shear rate from 100 to 200 s^-1

The abrupt change of the viscosity is caused by the shear thinning behaviour of the material and by the increase of the effect of convective mass-transfer on coarsening.

The growth of particles of A356 with 40% solid fraction is shown in Fig.5. The mean diameter follows a linear relation with time according to Eq.(8).

The corresponding microstructures after 300 s and 10 800 s of shearing are shown in Fig.6. The particles have globular shape with shape factors between 0.6 and 0.8.

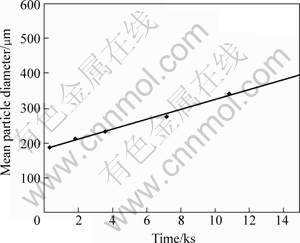
Fig.5 Mean particle diameter as function of shear time of A356 with φ_s of 40% and shear rate of 100 s^-1

Fig.6 Microstructures of A356 with φ_s of 40% and shear rate of 100 s^-1 after shearing for different time: (a) 300 s; (b) 10 800 s

A comparison of the growth of the particles for both investigated alloys is shown in Fig.7. The relative change in diameter is sketched versus time difference. Both alloys follow the linear growth law. The critical shear rate for the transition between diffusion and convection dominated coarsening is 9 s^-1 for the A356 and 38 s^-1 for the Sn-Pb alloy. Both experiments have been performed with a shear rate of 100 s^-1, much significantly higher than the critical one. The shear rates have been calculated for the used Searl-geometry applying the method of the “representative shear rate”[18]. The gradient of the lines, which corresponds to the rate constant k, is 7.7×10^-5 s^-1  for the A356 and 3×10^-5 s^-1 for Sn-Pb alloy. The scaling time constant t^* can be calculated with Eq.(7) from the experimental conditions. For A356 it is 1.3 s and for Sn-Pb it is 0.28 s. Consequently, the dimensionless driving potential C is calculated to be 5.9×10^-5 for A356 and 1.0×10^-4 for Sn-Pb, respectively.

Fig.7 Dimensionless increase in mean particle diameter under shear rate of 100 s^-1 and φ_s of 40%

The influence of the shear rate on the particle growth has been quantified by experiments with different shear rates but identical border conditions for Sn-15%Pb alloy.

With Eq.(8) and the dimensionless potential difference, the scaling parameter for the time t^* has been calculated. The double logarithmic plot of the experimental results, Fig.8, shows the excellent agreement with Eq.(7) and underlines the influence of the shear rate on the speed of coarsening.

The application of Eq.(2) and Eq.(8) for the correction of results of long-term rheological experiments with semi-solid material is demonstrated in Fig.9. The black line shows the decreasing viscosity following the stepwise increasing shear rates. At the end of the experiment, the initial shear rate of 80 s^-1 is repeated. The viscosity is significantly lower than that at the beginning of the experiment as a result of the coarsening of the particles during the experiment. By adjusting the viscosity values, shear step by shear step- wise, using Eq.(2) and (7) and the kinetic parameters estimated experimentally, the influence of the increasing particle diameter can be eliminated. By this the true viscosity function can be calculated which is related to one particle size. The reference point in Fig.9 is the viscosity value at a shear rate of 80 s^-1 with a corresponding mean particle size of 215 μm. It is obvious that the shear thinning behaviour is less pronounced in the calibrated viscosity function.

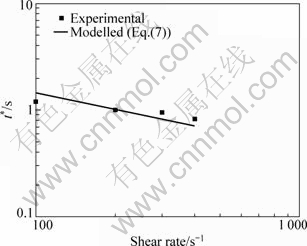
Fig.8 Scaling parameter for time t^* as function of shear rate of Sn-15%Pb with φ_s of 40%

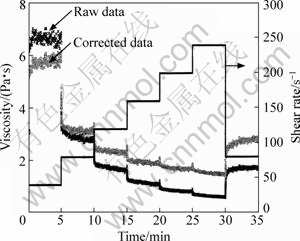
Fig.9 Shear rate experiment results with A356 under φ_s of 40%

6 Conclusions

It has been demonstrated that shearing of semi-solid alloys will increase the coarsening of the material. The model which has been set up allows for the forecast of this phenomenon. Its value has been demonstrated for the adjustment of long-term rheological experiments to gain true viscosity functions.

References

[1] LIFSHITZ I M, SLOYOZOV V V. The kinetics of precipitation from supersaturated solid solutions [J]. J Phy Chem Solids, 1961, 19: 35-50.

[2] WAGNER C. Theorie der alterung von niederschl?gen durch uml?sung [J]. Z. Elektrochem, 1961, 65: 581-591.

[3] ATKINSON H V, LIU D. Microstructural coarsening of semi-solid aluminium alloys [J]. Mat Sci Eng A, 2008, 96: 439-446.

[4] KOKE J, MODIGELL M. Flow behaviour of semi-solid metal alloys [J]. J Non-Newtonian Fluid Mech, 2003, 112: 141-160.

[5] KOKE J. Rheologie teilerstarrter Metalllegierungen [M]. Fortschr. Ber. VDI Reihe 5 Nr. 620, VDI Verlag, Düsseldorf, 2001.

[6] SEYHAN I, RATKE L, BENDER W, VOORHEES P W. Ostwald ripening of solid-liquid Pb-Sn dispersions [J]. Met Mater Trans A, 1996, 27: 2470-2478.

[7] SNYDER V A, ALKEMPER J, VOORHEES P W. Transient Ostwald ripening and the disagreement between steady-state coarsening theory and experiment [J]. Acta Meter, 2001, 49: 699-709.

[8] AKAIWA N, HARDY S C, VOORHEES P W. The effect of convection on Ostwald ripening in solid-liquid mixtures [J]. Acta Metal Mater, 1991, 39(11): 2931-2942.

[9] RATKE L, THIERINGER W K. The coarsening of liquid Al-Pb-dispersions [J]. Acta Metall, 1985, 33: 1793-1802.

[10] DIEPERS H J, BECKERMANN C, STEINBACH I. Simulation of convection and ripening in a binary alloy mush using the phase-field method [J]. Acta Mater, 1999, 47(13): 3663-3678.

[11] WAN G, SAHM P R. Particle characteristics and coarsening mechanisms in semi-solid Sn15%Pb alloy [C]//BROWN S B, FLEMINGS M C. Proceedings of the Second International Conference on the Semi-Solid Processing of Alloys and Composites. Massachusetts, 1992: 328-335.

[12] FAN Z, LIU G, HITCHCOCK M. Solidification behaviour under intensive forced convection [J]. Mater Sci Eng A, 2005, 413/414: 229-235.

[13] MODIGELL M. The application of modelling and rheology in SSM processing [C]//ALEXANDROU A. Proceedings of the 8th International Conference on Semi-Solid Processing of Alloys and Composites. Limassol, Cyprus, 2004.

[14] MACOSKO C W. Rheology: Principles, measurements and applications [M]. New York: VCH, 1994: 457.

[15] WINDHAB E. Fluid immobilization–A structure-related key mechanism for the viscous flow behaviour of concentrated suspension systems [J]. Applied Rheology, 2000, 10(3): 134-144.

[16] QUEMADA D. Rheology of concentrated disperse systems and minimum energy dissipation principle. Part I: viscosity concentration relationship [J]. Rheologica Acta, 1977, 16: 82-94.

[17] QUEMADA D. Rheology of concentrated disperse systems and minimum energy dissipation principle. Part II: a model for non-newtonian shear viscosity in steady flow [J]. Rheologica Acta, 1978, 17: 632-642.

[18] SCH?MMER P, WORTHOFF R H. An elementary method fort he evaluation of a flow curve [J]. Chem Eng Sci, 1978, 33: 759-763.

(Edited by YANG Bing)

Corresponding author: M. MODIGELL; Tel: +49-241-80-95159; E-mail: michael.modigell@avt.rwth-aachen.de

DOI: 10.1016/S1003-6326(09)60360-5