Trans. Nonferrous Met. Soc. China 28(2018) 328-339

Effects of backward path parameters on formability in conventional spinning of aluminum hemispherical parts

Tian GAN^1,2, Zhong-qi YU^1,2, Yi-xi ZHAO^1,2, S. A. EVSYUKOV³, Xin-min LAI^1,2

1. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China;

2. Shanghai Key Laboratory of Digital Manufacture for Thin-walled Structures, Shanghai Jiao Tong University, Shanghai 200240, China;

3. Faculty MT6, Bauman Moscow State Technical University, Moscow 105005, Russia

Received 30 September 2016; accepted 20 February 2017

Abstract: During multi-pass conventional spinning, roller paths combined with the forward and the backward pass are usually used to improve the material formability. In order to understand the backward spinning process properly, the backward roller paths of hemispherical parts with aluminum alloy 2024-O are analyzed. Finite element model with parameterized conventional spinning roller paths, which are based on quadratic Bezier curves, is developed to explore the evolution of the stress, strain and thinning during the backward processes. Analysis of the simulation results reveals stress and strain features of backward pass spinning. According to the findings, the application of the backward pass can obviously improve the uniformity of wall thickness. Furthermore, references of the parameters in future backward path design are provided.

Key words: conventional spinning; multi-pass forming; roller path design; backward pass

1 Introduction

Metal spinning process consists of rigidly clamping a blank against a mandrel by a tailstock, and gradually forcing the blank onto the mandrel with the roller. During the process, both the mandrel and blank are rotated while the roller moves along a designed roller path [1]. The inherent advantages of spinning, such as simple tooling, low forming loads and flexibility of the process, make it widely used in aerospace industries for producing lightweight parts [2-4]. The metal spinning is generally classified into three processes: conventional spinning, shear spinning and tube spinning. Conventional spinning is defined as the process with a constant thickness but a changeable diameter of the blank, while shear spinning is a process with a constant diameter but a sine law determined thickness of the blank [5]. Although the classification of metal spinning was described as above, some researchers [6] verified that thickness reduction happens in both conventional spinning and shear spinning. Based on experiments and numerical models, QUIGLEY and MONAGHAN [7,8] also observed that the first pass in conventional spinning is similar to that in shear spinning process.

Most of the published researches on conventional spinning are concentrated on studying the effects of roller nose radius, feed ratio and rotation speed on tool force and part geometry [9,10]. Many studies about roller path design are focused on one-pass conventional  spinning [11] or relied on empirical methods. While one- pass conventional spinning, limited by the formability, tends to wrinkle and fracture. In the view of RUNGE [5] and LANGE [12], multi-pass should be performed to form the part without wrinkling defects in conventional spinning. The shape of roller path in each pass plays an important role in achieving target geometries during the process of multi-pass conventional spinning. According to the moving direction of the roller, the forward pass and backward pass are defined, as shown in Fig. 1. During the forward pass, the roller moves towards the edge of the blank, and tensile radial stress and compressive tangential stress are generated in the roller contact region. During the backward pass, the roller moves in the reverse direction—towards the centre of the blank, and compressive radial stress and compressive tangential stress are caused [5,12] in the roller contact region.

Fig. 1 Stress distributions in roller contact region

ZHAN et al [13,14] researched the wall thickness and the forming mechanism of defects with a kind of specific multiple roller path; however, the generation of multi-pass in conventional spinning was not studied thoroughly. KANG et al [6,15] experimentally investigated three types of roller paths (linear, concave and convex) and stated that the deformation in the first pass has a decisive effect on the wall thickness distribution of the product. HAYAMA et al [16-18] concluded that concave roller path gives the best results and recommended involute path. Based on the involute equation, researchers [19-21] have systematically proposed the method to generate a desirable involute roller path in multi-pass conventional spinning. WANG and LONG [22] numerically analysed the effects of four different roller paths, i.e. combined concave and convex, convex, linear, and concave, on tool forces, wall thickness and stress distributions in conventional spinning, and concluded that concave roller path resulted in severer thinning. LI et al [23] developed parameterized roller paths with three times Bezier curve in the first pass of die-less spinning, and concluded that the location of severe thinning area moves backwards from the middle part of the blank to the end part with the increasing of curvature. POLYBLANK and ALLWOOD [24] performed a set of experiments to investigate how tool force, part geometry and various failure modes evolve with the change of parameters of quadratic Bezier curve in the first pass. Furthermore, they suggested that the influence of the backward pass on wrinkling or thinning should be further studied.

The published studies give an insight into roller path design in conventional spinning. However, in these researches, roller path design was almost focused on one-pass conventional spinning, and limited investigations were carried out on multi-pass. Moreover, the majority of the works were only concentrated on the forward passes. The backward pass is widely used in industry to produce parts. Therefore, it is of vital significance to study the backward pass in multi-pass conventional spinning. To explore thinning, stress and strain distributions during the backward pass multi-pass conventional spinning simulations including both the forward and backward passes with quadratic Bezier curves are established.

2 Methodology

2.1 Roller paths parameterization

Researchers who explore roller path have a preference for involute paths, while the process of generating involute curves is complex. There is a gap between academic outcomes and requirements of automatic roller path generation in industry. Bezier curve is determined by its control points, as shown in Fig. 2(a). Because the curve can be intuitively manipulated by its control points, it is widely used in computer graphics to model smooth curves. In this work, by taking advantage of the convenient curve definition, roller paths with parameterized Bezier curves are performed to explore the influence of the backward pass. The key feature in roller path design is to allow variable but smooth changes of curvature through the path, and the quadratic Bezier curve is sufficient for this requirement. A concave roller path is beneficial, as widely reported in the literature: the tendency to wrinkle is reduced if a more concave tool path is used, because of the reduction of the tool force near the workpiece perimeter [24]. Thus, the quadratic Bezier curve in concave form is applied in conventional spinning of hemispherical parts.

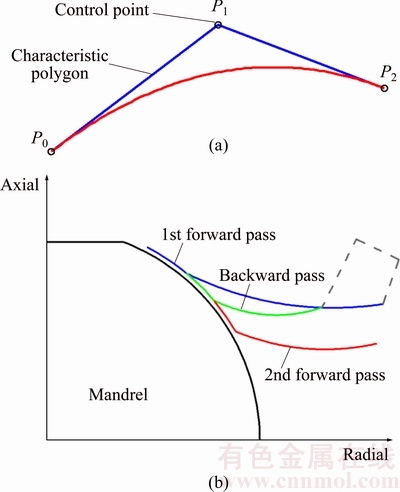
Fig. 2 Quadratic Bezier curve (a) and multiple roller passes (b)

The control point of the roller path is defined at the centre of the roller nose. As shown in Fig. 2(b), each pass consists of two parts: one part is determined by the shape of the mandrel, and the other is quadratic Bezier curve. The quadratic Bezier curve (Fig. 2(a)) is determined by three control points, P₀, P₁ and P₂.

In order to study the influence of the backward pass, at least three passes with two forward passes and one backward pass are needed. The backward pass used in this work is parameterized in Fig. 3(a). In order to make the findings applicable for other sizes of parts, we set the parameters as the percentage of distance. Z₁ is the radial distance between the ending point of the 1st forward pass and the outer surface of the mandrel. The ending point of the 1st forward pass moves a distance of Z_f in radial direction, and then the corresponding point at the 1st forward pass is the starting point P^′₀ of the quadratic Bezier curve in the backward pass. Z_f is the f percent of the length of Z₁. The selection principle of the starting point in backward pass takes LI et al’s [25] study as a reference. The control point P^′₂ is determined by the angle of θ, which is relative to the last contact point between the workpiece and the mandrel during the previous forward pass. The control point P^′₁ is defined relative to the mid-point of straight-line P^′₀P^′₂, and the mid-point moves U^′_n in the direction perpendicular to P^′₀P^′₂.  Increasing  U^′_n  leads  to  a  more  concave roller  path.

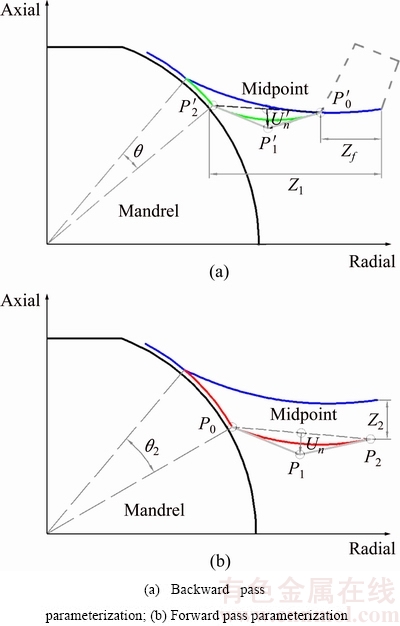
Fig. 3 Roller path parameterization

U^′_n is n percent of the length of P^′₀P^′₂. In summary, we set three parameters, f, θ and n, to describe the backward pass.

Usually, the backward pass follows behind the forward pass, and thus the forward pass needs to be designed firstly. Figure 3(b) shows the parameterization of the forward pass. The ending point P₂ is determined by the axial coordinate Z₂ measured from the ending point of the previous forward pass to the end of this pass. The definitions of P₀ and P₁ are similar to those in the backward pass. By taking reference of the previous works in Ref. [26], the parameters of the forward passes are chosen as θ₂=10°, Z₂=8 and U_n=4.5. To analyse the effect of the backward pass, roller paths with and without the backward pass are generated. The roller path without the backward pass is shown in Fig. 3(b), while the roller path including the backward pass is shown in Fig. 2(b). Moreover, 18 representative roller paths with different sets of parameters of θ, f and n are selected to study the backward pass.

2.2 Setting of basic parameters

The material used in this work is aluminum alloy 2024-O with a diameter of 200 mm and a thickness of 1.8 mm. A spinning speed of 200 r/min and a roller feed rate of 200 mm/min are used both in experiment and FE simulation. The angle between the axis of the mandrel and the axis of the roller is 40°. The experiments are all conducted on a horizontal spinning machine. A schematic diagram of spinning experiments is shown in Fig. 4.

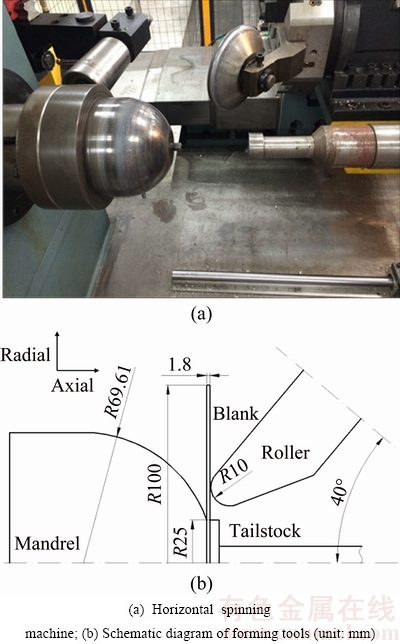
Fig. 4 Metal spinning experiments

2.3 Finite element analysis

The metal spinning processes are modelled using the commercial software ABAQUS. Considering the large deformation and complex contact conditions during this process, dynamic explicit solver is used in the dynamic spinning process simulation [27,28]. In the FE simulation, the forming tools, e.g. the roller, tailstock and mandrel, are modelled using 3D analytical rigid bodies. The improvement of the computational efficiency is one of the principal advantages of representing the forming tools as rigid bodies instead of deformable bodies. The blank, the only deformable part, is modelled using 8-node 3D reduced integration continuum shell element, the number of elements is 4956 and the number of nodes is 9576. The aluminum alloy 2024-O is assumed to be homogeneous and isotropic, with an elastic modulus of 71.3 GPa, a Poisson ratio of 0.33 and a mass density of 2780 kg/m³. The plastic behaviour is described by the von Mises criterion and the Hollomon strain-hardening law 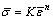(where K=308.62 MPa and n=0.234). Coulomb friction is assigned between the blank and the tools with three contact pairs: tailstock-blank 0.5, mandrel-blank 0.2, and roller-blank 0.02. To assure that the blank is clamped between the mandrel and the tailstock, a compressive force of 60 kN is set at the tailstock. The rotational velocity of mandrel and the roller feed rate are consistent with the experiment. A mass scaling factor of 25 is used to speed up the FE simulation. In this work, a global cylindrical coordinate system is used to analyse the evolution of the stress and strain, as shown in Fig. 5.

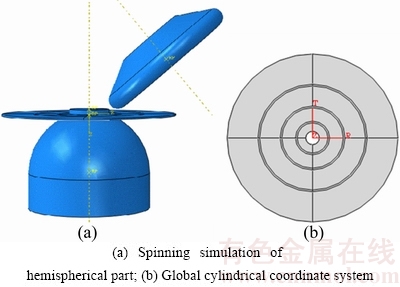
Fig. 5 Finite element model

3 Results and discussion

3.1 Verification of FE model

The simulation models are verified by studying the wall thickness and the energy histories of spinning processes. Experiments with one-pass conventional spinning to 45° are applied. A laser scanning 3D measurement system named FARO is used to obtain the wall thickness distribution of experimental spinning workpiece, as shown in Fig. 6.

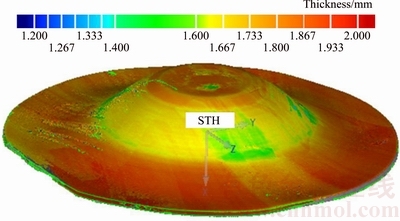
Fig. 6 Thickness distribution of experimental spinning workpiece

At the same time, the roller path used in the FE model is in accord with the experiment. The wall thickness obtained from FE simulation models is compared with that of the experiment, as shown in Fig. 7(a). The number of elements in models (a), (b) and (c) are 1936, 4956 and 9000, respectively. The deviation between the simulation and the experiment in region M (the deformed region) is smaller than that in region N (the flange of the workpiece), and as the grid density increases, the deviation becomes smaller. The maximum error of thinning between the experimental and simulated values is about 4%. Deviations within 10% are acceptable. By considering the computational efficiency and precision, the grid density of model (b) is used in the simulation of this work.

Fig. 7 Verification of FE model

The energy histories of model (b) are studied to evaluate the accuracy of the simulation. To ensure that the simulation results are not significantly affected by mass scaling, the ratio of the kinetic energy to the internal energy of the blank should not be greater than 10% during most time of the process. Moreover, the artificial strain energy should also be less than 5% of the internal energy to avoid the hourglass problem, which causes the shear locking phenomenon in the reduced integration linear elements and reduces simulation accuracy. As shown in Fig. 7(b), at the beginning of the process, because of the rotational acceleration of the blank, the ratio of the kinetic energy to internal energy is much larger than 10%. However, during most time of the process, the ratio is below 10%. The ratio of the artificial strain energy to the internal energy is below 5% throughout the process. Therefore, the dynamic problem caused by mass scaling and the hourglass problem are well controlled.

3.2 Analysis of deformation method for first pass

The deformation in the first pass has a significant effect on the wall thickness distribution of the product [6], and a wide ring-shaped contact region between workpiece and mandrel can avoid failures such as wrinkling or fracture. Experiments carried out by QUIGLEY and MONAGHAN [7] indicated that there was some degree of shear forming involved in the first pass of conventional spinning. Therefore, it is certain that the clearance exists between the mandrel and the inner surface of workpiece. Three different paths of the first pass with different clearances between the mandrel and the roller are analysed (the original thickness of the blank is 1.8 mm): 1) conventional spinning to 40° with the clearance of 1.8 mm; 2) conventional spinning to 40° with the clearance of 1.65 mm; 3) shear spinning as sine law to 40°. Figure 8(a) presents the thickness distribution of different paths in the first pass, and Fig. 8(b) shows the fitability of the spinning workpiece with the mandrel.

From Figs. 8(a) and (b), conventional spinning with the clearance of 1.8 mm has the smallest thinning, while the fitability is the worst, which cannot build a wide ring-shaped contact region. Shear spinning has the smallest clearance while the thinning is the severest. Thus, the conventional spinning to 40° with the clearance of 1.65 mm is selected as the first pass. The deformation of the first forward pass is 40°; in other words, the radial distance of the last contact region between the workpiece and the mandrel is about 46 mm. It is clearly observed that the wall thickness reduces significantly in the last contact region (as shown in Fig. 8(a)).

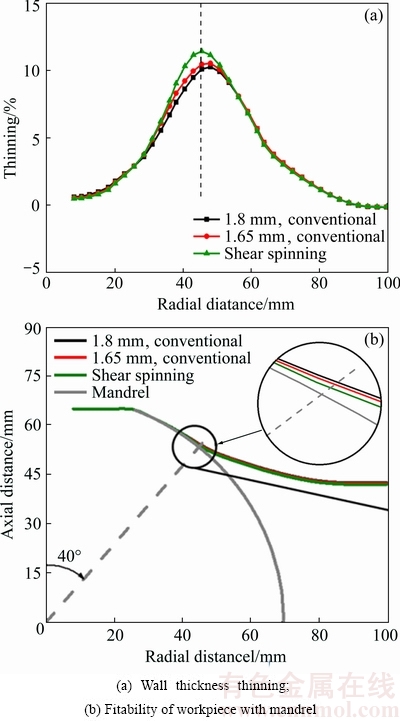
Fig. 8 Analysis of first pass

3.3 Analysis of deformation mechanics for backward pass

3.3.1 Strain of backward pass

To comprehensively understand the backward pass process, variations of strains of the backward pass are compared with the results of the first forward pass. The backward pass with f=44%, θ=8.5° and n=16%, which endures the maximum thinning during the analysis of the backward pass, is chosen as a representative of the backward pass to analyse strains in this section and stresses in the next section. The contact position between the workpiece and the roller in the backward pass as well as the position in the forward pass is located at the same places with radial coordinates of about 60 mm. During the forward pass, region A is located behind the roller and region B is located in front of the roller. In contrast, during the backward pass, region C is located in front of the roller and region D is located behind the roller.

As revealed in Fig. 9(a), high tensile radial strains distribute on the top surface and bottom surface in region A; besides, small tensile radial strains on both top and bottom surfaces are observed in region B during the forward pass. Radial strains during the backward pass are described in Fig. 9(b). The high tensile radial strains in region D result in significant wall thickness reduction. The above preliminary analysis reveals that both in the forward pass and backward pass the severe thinning region of the workpiece has tensile radial strains on both top and bottom surfaces.

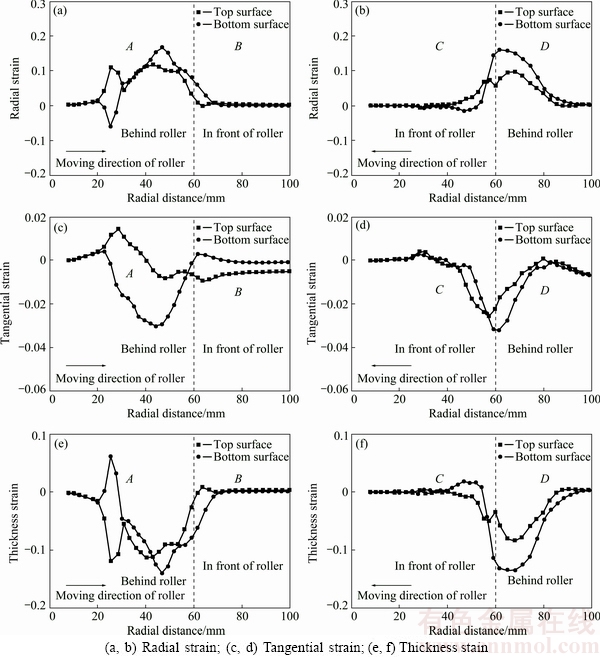
Fig. 9 Strain comparison between forward pass (a, c, e) and backward pass (b, d, f)

During the forward pass, region A has tensile tangential strains on the top surface, while compressive tangential strains on the bottom surface. Tangential strains presented in Fig. 9(c) illustrate that both in region A and region B there are opposite states of strains on top surface and bottom surface. While the top surface and bottom surface have the same states of tangential strain during the backward pass, in other words, they have tensile or compressive tangential strains at the same time. Furthermore, the compressive tangential strain in region D will lead to the increasing of the wall thickness in some degree.

As shown in Fig. 9(e), during the forward pass, apart from the bottom surface of the workpiece ahead of region A, high compressive thickness strains on both top and bottom surfaces are observed, which results in severer thinning of the workpiece. The bottom surface ahead of region A is under tensile thickness strain, which indicates the improvement of wall thickness. However, the tensile thickness strain is smaller than the compressive thickness strain on top surfaces; therefore, the wall thickness in this region is decreased. The variations of thickness strain in the backward pass are illustrated in Fig. 9(f), in comparison with region A during the forward pass, the thickness strain in region D during the backward pass has the same tendency. Conversely, the tensile thickness strain on the bottom surface in region C is larger than the compressive thickness strain on the top surface, and consequently, the wall thickness increases in region C, which explains the thickness improvement around point 2 (will be mentioned in Section 3.3.3).

Clearly, the distributions of strains in the backward pass are similar to those in the forward pass, which indicates that the distributions of strains are not associated with the travel direction of the roller.

3.3.2 Stress of backward pass

Variations of stresses in the backward pass are also compared with those in the forward pass. The roller is located at the same place mentioned in Section 3.3.1. In order to further investigate the stress distributions, the workpiece is artificially divided into two regions, respectively, in the forward pass and in the backward pass, as shown in Fig. 10. Region E and region H are located behind the roller where the material has already been formed; region F and region G are located in front of the roller where the material will be formed in the next step. Point 1 is the roller contact point, which is located at the position with radial coordinate of about 60 mm.

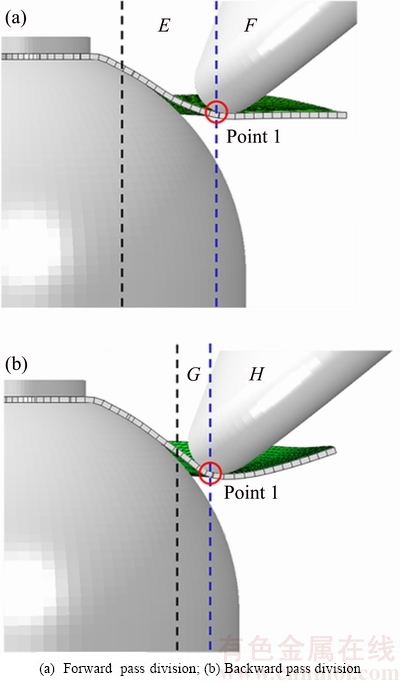
Fig. 10 Artificial division of workpiece

The value of radial stress is often used as the criterion of the cracking limit, so its distribution laws can provide reference for determining cracking failure in multi-pass spinning [11]. The roller moves towards the edge of the blank in the forward pass. As shown in Fig. 11(a), the top surface of the workpiece is subjected to tensile radial stress in region E and compressive radial stress in region F, while the bottom of the workpiece is subjected to the opposite radial stress conditions. Moreover, tensile radial stresses are observed on both top and bottom surfaces at the roller contact point. Thus, with the roller contact point as a boundary, the region behind the roller (region E) and the region in front of the roller (region F) are subjected to conversely directed radial bending effects. The roller moves towards the center of the blank in the backward pass. The radial stress variations in the backward pass are shown in Fig. 11(b). Compared with the forward pass, the radial stresses in the backward pass have the same stress conditions in the region behind the roller (region H) as well as the region in front of the roller (region G). However, both top and bottom surfaces at roller contact point are subjected to compressive radial stresses, which are tensile stresses in the forward pass.

The distribution laws of tangential stress can serve as a significant guide to the determination of the critical condition of wrinkling in multi-pass spinning [11]. Figures 11(c) and (d) illustrate the tangential stress variations of the forward pass and backward pass. Region E and region H are subjected to tensile tangential stresses on the top surface and compressive tangential stresses on the bottom surface. At the same time, Figs. 11(c) and (d) reveal the compressive tangential stresses on the top surface and tensile tangential stresses on the bottom surface in region F and region G. As the radial stress analysed above, there are also two opposite direction bending effects in tangential direction. At the roller contact point in the forward pass, the compressive tangential stress is generated on the top surface, and the tensile tangential stress is subjected on the bottom surface. Additionally, the top surface of the roller contact point in the backward pass is under compressive tangential stresses, and the bottom surface is under tensile tangential stresses.

Consequently, 1) both in the forward pass and in the backward pass, the region behind the roller contact point is subjected to tensile radial and tangential stresses on the top surface, while compressive radial and tangential stresses on the bottom surface, as summarized in Table 1; 2) both in the forward pass and backward pass, the region in front of the roller is observed with compressive radial and tangential stresses on the top surface, while tensile radial and tangential stresses on the bottom surface; 3) in the forward pass, the roller contact point is under tensile radial stresses and compressive tangential stresses on the top surface; 4) in the backward pass, the roller contact region is under compressive radial stresses and compressive tangential stresses on the top surface. These demonstrate the findings of RUNGE [5] and LANGE [12].

3.3.3 Thinning of backward pass

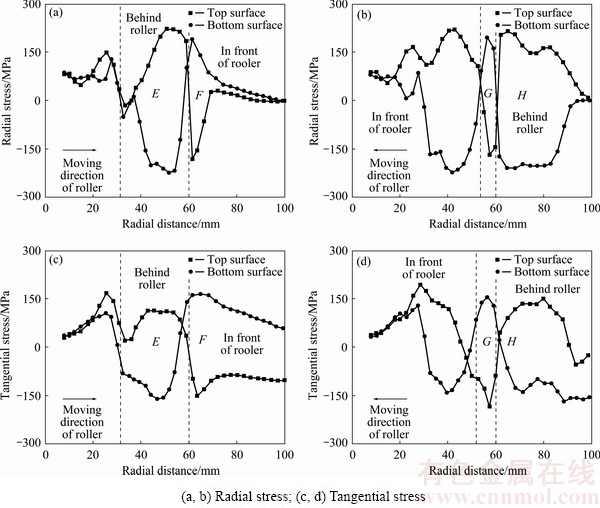
Fig. 11 Stress comparison between forward pass (a, c) and backward pass (b, d)

Table 1 Variations of stresses in forward and backward passes

The wall thickness distribution in the backward pass varies with different set of parameters in roller paths. Parameter f determines the radial distance between the ending point of the first forward pass and the starting point of the backward pass. Figure 12(a) shows the schematic diagram of different backward paths with the change of parameter f. Figure 12(b) illustrates the thinning along the radial direction of the workpiece with changeable values of f while unchangeable values of θ and n. There is a certain degree of thickness improvement around point 2, in contrast, significant thinning in region J (the flange of the workpiece). Point 2 endures the severest thinning during the first forward pass. The thickness improvement around point 2 indicates that the backward pass can force the material to flow back. Region J is the flange of the workpiece, and the maximum thinning positions in this region vary with the lowest positions of the concave backward path. With the decreasing of f, the wall thickness in the backward pass is seriously reduced. Because the distance from the starting point of the backward pass to the edge of the blank decreases, the larger volume of the material involves in flowing back. The corresponding relationship was also obtained by LI et al [25].

Parameter θ is the deformation between the first forward pass and the backward pass. Figure 12(c) shows the roller paths with different values of θ. Consistent with the result above, the wall thickness increases in point 2, while decreases in region J. However, the radial coordinates of the maximum thinning positions in region J stay substantially unchanged, which may result from the minor changes of the radial coordinate of the lowest position of the concave backward path. During the spinning process, the amount of deformation between two passes plays a decisive role in the wall thickness thinning. Consequently, the thinning phenomenon becomes severer with the increasing of θ.

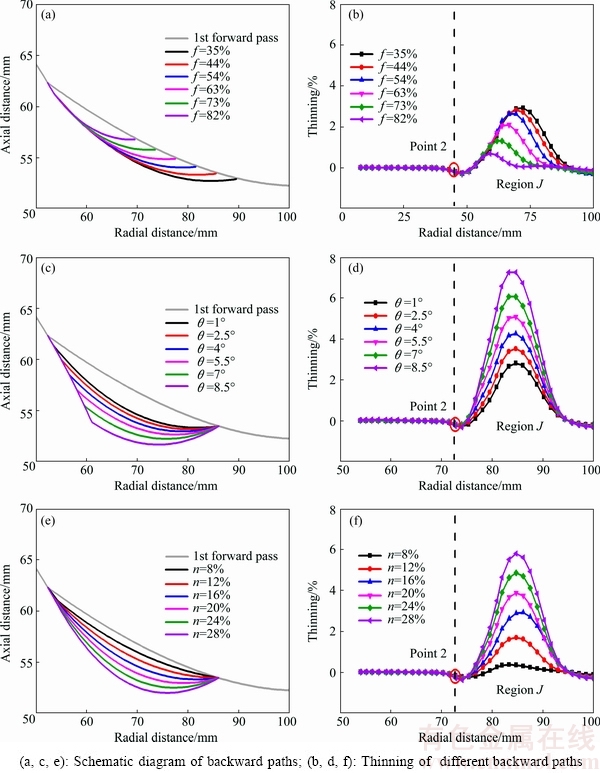
Fig. 12 Effects of parameters on thinning in backward pass

The increasing of parameter n leads to a more concave roller path, as shown in Fig. 12(e). As illustrated in Fig. 12(f), point 2 and region J have the same thinning phenomenon as the results of parameter θ, and the severest thinning positions are almost unchanged in the radial direction. POLYBLANK and ALLWOOD [24] found that an increasing concave roller path leads to a significant increase in the average tool force, particularly in the middle of the path, which leads to increased thinning correspondingly. The increasing n leads to a more concave roller path, and similarly, the thinning phenomenon becomes severer.

The results indicate, in all, that 1) the application of the backward pass can increase wall thickness in the severest thinning region during the first forward pass, 2) with the decreasing of f, the wall thickness in the backward pass is seriously reduced; on the contrary, with the increasing of θ and n, the wall thickness reduction phenomenon of the backward pass becomes severer, and 3) the radial coordinate of the lowest position of the concave backward path determines the position of the severest thinning region.

3.4 Thinning effect of backward pass on multi-pass spinning

In order to analyse the effects of the backward pass on thinning in multi-pass conventional spinning, thinning with roller paths in Fig. 13(a) is compared with thinning using roller paths in Fig. 13(b). The forward passes in Fig. 13(a) are exactly the same as those in Fig. 13(b). The deformation between the first forward pass and the second forward pass is 10°; more specifically, after the second forward pass, the last contact point between workpiece and mandrel is located at the position of  54.7 mm in the radial direction. As revealed in Fig. 14(a), point 3 is the last contact point between workpiece and mandrel in the second forward pass. The position of point 3 has the severest thinning in the second forward pass.

For more intuitive analysis, Figs. 14(b-d) show the deviations of thinning between roller paths with the backward pass (Fig. 13(a)) and roller paths without the backward pass (Fig. 13(b)). The total thinning results of different roller paths are obtained by adding the thinning deviation results shown in Figs. 14(b-d) to the thinning results shown in Fig. 14(a). Figures 14(b-d) suggest that the using of the backward pass can improve the wall thickness in region R, and this region is under severe thinning in Fig. 14(a). Furthermore, the using of the backward pass decreases the wall thickness in region S, and the thinning in this region is much smaller than that in region R, as shown in Fig. 14(a). On one hand, the using of the backward pass increases the wall thickness in severe thinning region. On the other hand, it decreases the wall thickness in another region, which endures smaller thinning. Overall, the conclusion can be drawn that the using of the backward pass can obviously improve the uniformity of wall thickness. When θ=1°, it can be considered that there is nearly no deformation between the first forward pass and the backward pass; in other words, the ending point of this situation is coincident with the last contact point in the first forward pass. Figure 14(c) of θ=1° indicates that the uniformity of wall thickness is still improved when there is no deformation between the forward and backward pass.

By comparing with different backward passes, the improvement of uniform wall thickness is much more sensitive to parameter θ, and parameter n also has obvious effects on improving the uniformity of wall thickness, while the changing of parameter f does not result in the obvious improvement as the other two parameters. It is clearly illustrated in Fig. 14 that, with the increasing of the values of θ and n, the uniformity of wall thickness is improved. On the contrary, the uniformity of wall thickness is improved with the decreasing of parameter f. Based on the findings mentioned above, references of the parameters are provided during the future design of the backward pass with the quadratic Bezier curve. According to different parts and different spinning processes, we can appropriately choose large values of θ and n, while small value of f.

Fig. 13 Schematic diagrams of multi-pass spinning

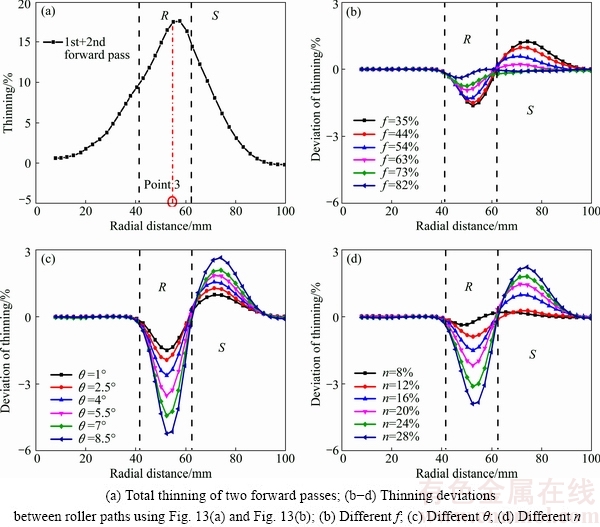
Fig. 14 Thinning effect of backward pass on multi-pass spinning

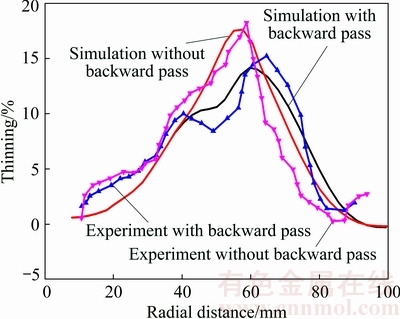
Fig. 15 Experimental verification of multi-pass spinning

The simulation results of the multi-pass conventional spinning are verified by experiments, as shown in Fig. 15. The wall thickness thinning of tool paths with backward pass and tool paths without backward pass are well matched during the former region, because of the same using of the first forward pass. In addition, the experimental result verifies the conclusion drawn by simulation that the using of backward pass can improve the uniformity of wall thickness. Figure 15 illustrates that the maximum error of thinning between the experimental and simulated values is within 10%, which is considered acceptable.

4 Conclusions

1) The similar strain distributions between the forward pass and backward pass indicate that the distributions of strains are not associated with the travel direction of the roller. However, the stress distributions are relevant to the roller travel direction. Both in the forward pass and backward pass, the region behind the roller contact point is subjected to tensile radial and tangential stresses on the top surface, while the region in front of the roller is subjected to compressive radial and tangential stresses on the top surface.

2) With the decreasing of f, the thinning of the backward pass becomes severer; on the contrary, with the increasing of θ and n, the thinning phenomenon of the backward pass becomes severer.

3) Application of the backward pass can obviously improve the uniformity of wall thickness in multiple roller path design. Appropriate large values of θ and n, and small value of f are recommended during the design of the backward pass with the quadratic Bezier curve in multi-pass conventional spinning.

References

[1] ZHAN Mei, WANG Qiao-ling, HAN Dong, YANG He. Geometric precision and microstructure evolution of TA15 alloy by hot shear spinning [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 1617-1627.

[2] WONG C C, DEAN T A, LIN J. A review of spinning, shear forming and flow forming processes [J]. International Journal of Machine Tools and Manufacture, 2004, 43: 1419-1435.

[3] XIA Qin-xiang, XIAO Gang-feng, LONG Hui, CHENG Xiu-quan, SHENG Xian-fei. A review of process advancement of novel metal spinning [J]. International Journal of Machine Tools & Manufacture, 2014, 85: 100-121.

[4] ZHAN Mei, YANG He, GUO Jing, WANG Xian-xian. Review on hot spinning for difficult-to-deform lightweight metals [J]. Transactions of Nonferrous Metals Society of China, 2015, 25: 1732-1743.

[5] RUNGE M. Spinning and flow forming [M]. POLLITT D H, Trans. Leifield GmbH, 1994.

[6] KANG Da-chang, GAO Xi-cheng, MENG Xiao-feng, WANG Zhi-hui. Study on the deformation mode of conventional spinning of plates [J]. Journal of Materials Processing Technology, 1999, 91: 226-230.

[7] QUIGLEY E, MONAGHAN J. Using a finite element model to study plastic strains in metal spinning [C]//Proceedings of the 9th International Conference on Sheet Metal. Leuven, Belgium, 2001: 255-262.

[8] QUIGLEY E, MONAGHAN J. Metal forming: an analysis of spinning processes [J]. Journal of Materials Processing Technology, 2000, 103: 114-119.

[9] MUSIC O, ALLWOOD J M, KAWAI K. A review of the mechanics of metal spinning [J]. Journal of Materials Processing Technology, 2010, 210: 3-23.

[10] XIA Qin-xiang, ZHANG Peng, CHENG Xiu-quan, YANG Bao-jian. Orthogonal experimental study on forming process parameters of tube stagger spinning [J]. Forging & Stamping Technology, 2012, 37: 42-46. (in Chinese)

[11] LIU Jian-hua, YANG He. A study of the stress and strain distributions of first-pass conventional spinning under different roller-traces [J]. Journal of Materials Processing Technology, 2002, 129: 326-329.

[12] LANGE K. Handbook of metal forming [M]. New York: McGraw-Hill, 1985.

[13] ZHAN Mei, LI Hu, YANG He, CHEN Gang. Wall thickness variation during multi-pass spinning of large complicated shell [J]. Journal of Plasticity Engineering, 2008, 15: 115-121. (in Chinese)

[14] SONG Xiao-fei, ZHAN Mei, JIANG Hua-bing, LI Tian, YANG He. Forming mechanism of defects in spinning of large complicated thin-wall aluminum alloy shells [J]. Journal of Plasticity Engineering, 2013, 20: 31-36. (in Chinese)

[15] KANG Da-chang, GAO Xi-cheng, MENG Xiao-feng. Study on deformation mode of conventional spinning of plates [J]. Journal of Plasticity Engineering, 1998, 5: 102-106. (in Chinese)

[16] HAYAMA M, KUDO H, SHINOKURA T. Study of the pass schedule in conventional simple spinning [J]. Bulletin of JSME, 1970, 13: 1358-1366.

[17] HAYAMA M, NAKAMURA M, WATANABE T, HAMANO H. Roller pass programming in conventional spinning by N.C. spinning machine [J]. Journal of the Japan Society for Technology of Plasticity, 1986, 27: 1053-1059.

[18] HAYAMA M. Roller pass programming and selection of working conditions in conventional spinning [J]. Journal of the Japan Society for Technology of Plasticity, 1989, 30: 1403-1410.

[19] LIU Jian-hua, YANG He. Development of multi-process conventional spinning and research on roller-trace [J]. Mechanical Science and Technology, 2003, 22: 805-807. (in Chinese)

[20] LIU Xing-jia, ZHANG Yi-huang. How to select the moving passes of the spinning roller [J]. Journal of Plasticity Engineering, 1997, 4: 84-90. (in Chinese)

[21] CHEN Jia, WAN Min, LI Wei-dong. Design of the involute trace of multi-pass conventional spinning and application in numerical simulation [J]. Journal of Plasticity Engineering, 2008, 15: 53-57. (in Chinese)

[22] WANG Lin, LONG Hui. A study of effects of roller path profiles on tool forces and part wall thickness variation in conventional metal spinning [J]. Journal of Materials Processing Technology, 2011, 211: 2140-2151.

[23] LI Yong, WANG Jin, LU Guo-dong, PAN Guo-jun. A numerical study of the effects of roller paths on dimensional precision in die-less spinning of sheet metal [J]. Journal of Zhejiang University – Science A, 2014, 15: 432-446.

[24] POLYBLANK J A, ALLWOOD J M. Parametric toolpath design in metal spinning [J]. CIRP Annals-Manufacturing Technology, 2015, 64: 301-304.

[25] LI Xin-biao, HAN Zhi-ren, GAO Tie-jun, LIU Bao-ming, JIA Zhen. Finite element simulation of multi-pass spinning forming of large complex thin-wall cylinder [J]. Journal of Shenyang Aerospace University, 2016, 33: 32-37. (in Chinese)

[26] GAN Tian, KONG Qing-shuai, YU Zhong-qi, ZHAO Yi-xi, LAI Xin-min. A numerical study of multi-pass design based on Bezier curve in conventional spinning of spherical components [C]//RIGAUD L, SAANOUNI K. The 12^th International Conference on Numerical Methods in Industrial Forming Processes. Troyes, France, 2016: 80.

[27] LONG Hui, HAMILTON S. Simulation of effects of material deformation on thickness variation in conventional spinning [C]//The 9th International Conference on Technology of Plasticity. Gyeongju, South Korea, 2008: 735-740.

[28] ABAQUS analysis user’s manual [M]. USA: ABAQUS Inc., 2012, 12-13.

回程轨迹参数对铝合金球面件旋压成形性能的影响

甘 甜^1,2，于忠奇^1,2，赵亦希^1,2，S. A. EVSYUKOV³，来新民^1,2

1. 上海交通大学 机械系统与振动国家重点实验室，上海 200240；

2. 上海交通大学 上海市复杂薄板结构数字化制造重点实验室，上海 200240；

3. Faculty MT6, Bauman Moscow State Technical University, Moscow 105005, Russia

摘  要：在多道次普旋成形中，多采用往程和回程结合的旋轮轨迹形式来提高材料的成形性能。为了深入探究回程旋压，对2024-O铝合金半球件回程旋压轨迹进行研究。基于二次Bezier曲线，建立普旋回程旋轮轨迹的参数化设计方法；并结合有限元技术，分析回程轨迹参数对2024-O铝合金半球件旋压应力、应变和减薄率的影响规律。通过对回程旋压的仿真分析，揭示回程的应力和应变特点。结果表明，回程道次的使用可以明显提高铝合金球面件的壁厚均匀性；同时，揭示了Bezier曲线参数化选择与旋压厚度均匀性的关系。

关键词：普旋；多道次成形；轨迹设计；回程

(Edited by Bing YANG)

Foundation item: Project (2014CB046601) supported by the National Basic Research Program of China; Project (51675333) supported by the National Natural Science Foundation of China

Corresponding author: Zhong-qi YU; Tel: +86-21-34206785; E-mail: yuzhq@sjtu.edu.cn

DOI: 10.1016/S1003-6326(18)64666-7