DOI: 10.11817/j.issn.1672-7207.2015.11.051
高速列车通过带有套衬结构隧道气动效应分析
刘峰,姚松,杨明智,张洁
(中南大学 交通运输工程学院,轨道交通安全教育部重点实验室,湖南 长沙,410075)
摘要:采用三维、可压缩、非定常N-S方程的数值计算方法,对8辆编组的高速列车以300 km/h速度通过带有套衬结构隧道时车体表面及隧道壁面的瞬变压力进行分析。研究结果表明:数值计算结果与动模型实验结果较吻合,2种方法得到的压力曲线变化规律一致,幅值误差在5%以内;列车通过隧道时,车体头、尾处测点压力差别较大,中部测点压力差异较小;沿列车车身方向,测点正压幅值逐渐减小,负压幅值逐渐增大;隧道壁面测点压力峰峰值在隧道进、出口附近较小,而在靠近隧道中部时较大;隧道内安装套衬对于高速铁路双线隧道气动效应影响很小,加装套衬前后,测点压力幅值差异在2%以内。因此,建议在对高速铁路隧道病害整治中,考虑使用套衬技术。
关键词:高速列车;隧道;套衬;气动效应
中图分类号:U271.91;U25 文献标志码:A 文章编号:1672-7207(2015)11-4363-07
Analysis on aerodynamic effect of high-speed train passing tunnel with lining structures
LIU Feng, YAO Song, YANG Mingzhi, ZHANG Jie
(Key Laboratory of Traffic Safety on Track of Ministry of Education,
School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China)
Abstract: Based on unsteady N-S equation of three-dimensional and compressible viscous fluid, transient pressure of the train and tunnel was studied when an 8-car high-speed train passed a tunnel with lining structure at a speed of 300 km/h. The results show that the calculated results agree with those of the experimental model. The pressure curves attained by two methods are identical, and the difference of amplitudes is below 5%. The pressure changes of the measuring points in the head and end of the train are different, while those in the middle part of the train are almost the same. Along the direction of the body, the amplitude of positive pressure decreases gradually while the negative increases. The peak pressure values of measuring points around the inlet and the outlet on tunnel wall are less than those near the middle part of tunnel. Installing lining structure shows no significant effect on the aerodynamic effects of existing double-line tunnel, and the difference in maximum pressure values of measuring points is below 2%. Thus, the lining technology is proposed to be used in addressing the disease of high-speed railway tunnel.
Key words: high-speed train; tunnel; lining; aerodynamic effect
既有铁路隧道病害已成为了制约铁路提速和提高单线运载能力的瓶颈[1]。随着我国铁路事业的不断发展,隧道病害也必将成为高速铁路发展所面临和解决的重要问题。作为一种常见的病害整治措施,套衬补强技术就是在既有衬砌内表面再灌注一定厚度的混凝土,可阻止既有衬砌的进一步裂损变形,达到彻底根治的效果[2]。然而,套衬的加装同时会使隧道原有截面积发生改变,使得隧道内的气动效应受到影响,所以有必要对隧道加装套衬后的气动效应进行分析。相较于低速列车,高速列车通过隧道时所带来的气动效应要剧烈的多,其引发的隧道内的压力波动,会直接给列车运行安全性和乘员舒适性带来影响。国内外学者对于高速列车通过隧道气动效应的研究很多。Yamamoto[3]最早利用一维假设建立了隧道压力波的一维流动理论和特征线求解方法,Howe等[4-6]运用精确声学格林函数计算得到了列车进入隧道过程中隧道内压缩波的压力-时间曲线,并对各类的缓冲结构效果进行分析。骆建军等[7-8]采用实验和数值计算的方法得出列车速度以及隧道阻塞比是影响隧道压缩波的压力以及压力梯度的主要因素。赵文成等[9-10]通过模型试验和理论推导,得出了最大压力、最大压力梯度和列车速度、隧道阻塞比、车头长细比之间的理论关系式。马伟斌等[11-13]在2008—2009年和2009—2011年间,对于隧道气动效应进行了2次较为系统的研究,也得出了大量的相关规律和试验经验。针对隧道内加装套衬结构这一特殊情况进行研究的文献很少,为此,本文作者以某客运专线上的高铁隧道为研究对象,采用数值仿真和动模型实验相结合的方法,对列车以300 km/h速度通过该隧道时的车体表面、隧道壁面不同测点的空气压力变化进行分析,为高铁隧道内加装套衬结构提供气动依据。
1 数值模拟
依照所选列车及隧道的实际几何特征,建立了车隧耦合数值计算模型。高速列车模型采用了8辆编组,即头车、6节中间车和尾车,全长为201.4 m;隧道为双线隧道,全长为1 921 m,断面面积为100 m2;隧道入口端、出口端分别设有明洞缓冲结构和帽檐斜切段缓冲结构。车隧计算模型和计算区域分别如图1和图2所示。套衬结构起始端位于距隧道入口431 m处,全长为89 m,整个套衬段的厚度均为0.3 m,加装套衬段后,隧道有效净空断面积缩减为92.9 m2。隧道模型截面见图3。

图1 高速列车计算模型
Fig. 1 Calculation model of high-speed train
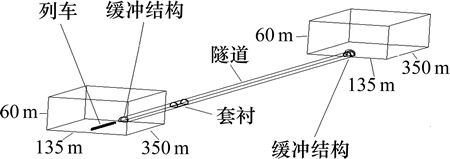
图2 计算区域
Fig.2 Computational zone
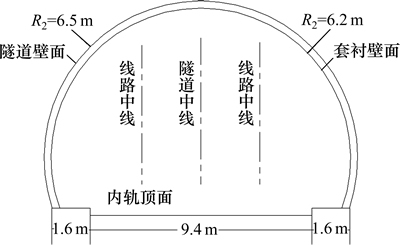
图3 隧道截面
Fig. 3 Section of tunnel
本文基于三维、非定常、可压缩、黏性流场对高速列车通过隧道进行流场数值分析,采用工程上应用广泛的k-ε湍流模型,详细流场控制方程及湍流模型参见文献[14]。为了解决高速列车与隧道之间的相对运动,网格方面采用分区对接滑移网格技术,即在有相对运动的不同网格间设置公共滑移界面,从而实现彼此的数据交换。列车、套衬及缓冲结构附近使用几何适应性良好的四面体网格,结构相对简单的流场区域采用六面体结构网格进行离散,划分的网格总数为500万左右。
列车车体表面测点分布如图4所示,车体表面两侧对称布置测点,共33个。由于列车在通过隧道时,车体中部压力变化较小,所以在头车和尾车布置测点较多,3号车至7号车只在每节车的中部对称布置2个测点,位置与2号车测点15和16相同。隧道壁面沿纵向方向不同位置和几个横断面上不同高度位置布置了多个测点。
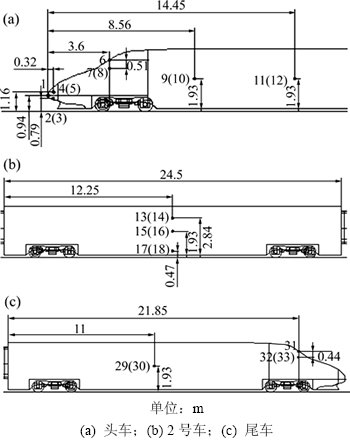
图4 列车模型测点布置图
Fig. 4 Points arrangement of train model
2 动模型实验验证
本实验室的列车气动性能模拟型动模型实验装置,可以真实再现列车高速通过隧道时的空气三维非定常流动现象,是目前国内最好的模拟车隧气动问题的专用大模型实验设备[15-17]。为了与数值计算相对应,本次动模型实验首次采用了8辆编组的模型列车,缩比为1:31,因此对列车运行平稳性提出了更高的要求。套衬结构的安装是依靠将模型隧道壁面向内加厚而实现的,如图5所示。
根据流动相似原理,动模型实验中模拟雷诺数是重要的相似准则,而当实验雷诺数大于临界雷诺数时,气动特性就不再随雷诺数变化而改变[15]。本次动模型实验车速为300 km/h,特征长度取模型车高0.119 m,20 ℃下的空气动力黏性系数为1.808×10-5 N·s/m2,空气密度为1.205 kg/m3,得出实验雷诺数为6.61× 105,大于临界雷诺数3.60×105(由实验测得),说明本次的实验满足相似性要求。
选取2种方法相同位置测点的压力变化曲线进行对比,为了与数值模拟计算的时间同步,将动模型实验所得数据图形的时间轴扩大了31倍。车体表面选用3号车中部测点,隧道壁面选用距隧道入口475 m处测点(套衬中心处),如图6和图7所示。由图6和图7可以看出:2种方法得到的车体及隧道壁面瞬变压力曲线变化规律基本一致,幅值误差在5%以内,从而验证了本文采用的数值计算方法可以较好地模拟高速列车通过隧道所引发的空气动力效应问题。

图5 隧道模型内套衬结构图
Fig. 5 Lining structure in tunnel model
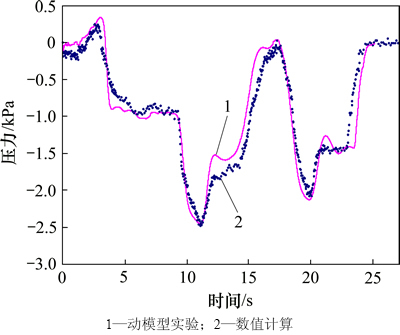
图6 车体表面19号测点压力变化曲线对比
Fig. 6 Comparison between two curves of pressure attained from two methods for measured point 19 on train
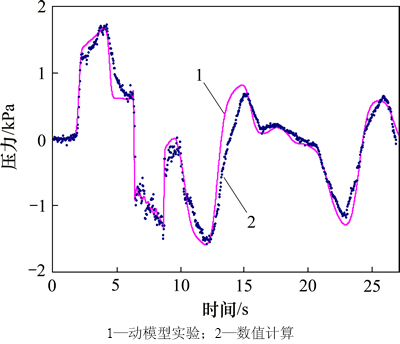
图7 隧道壁面475 m处测点压力变化曲线对比
Fig. 7 Comparison between two curves of pressure attained from two methods for measured point of 475 m on tunnel
3 列车通过带套衬结构隧道气动效应分析
3.1 瞬变压力时间历程分析
列车高速通过隧道时,产生的压缩波和膨胀波会在隧道内部不断的传播和反射,致使车体表面及隧道壁面压力发生剧烈变化。图8所示为列车在隧道中运行时测点压力变化与波系传播图,其中隧道壁面选取距入口415 m处测点,车体表面选取3号车中部测点。由图8可以看出:无论是隧道壁面还是车体表面,当压缩波经过时,测点压力会增大,对应图8中①,⑤,⑥,⑨,⑩和 ;而当膨胀波经过时,测点压力会减小,对应图8中②,⑦,⑧和
;而当膨胀波经过时,测点压力会减小,对应图8中②,⑦,⑧和 ;另外,当列车通过隧道壁面测点时,也会带动周围流场运动,使测点压力幅值下降,对应图8中③和④。
;另外,当列车通过隧道壁面测点时,也会带动周围流场运动,使测点压力幅值下降,对应图8中③和④。
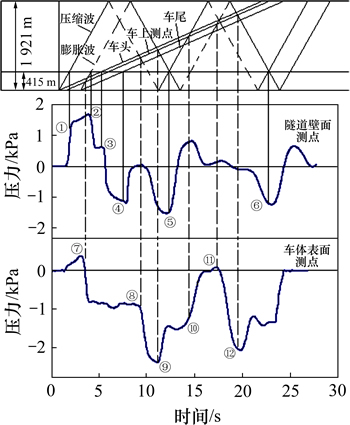
图8 测点压力变化与波系传播图
Fig. 8 Pressure change of measured points and wave spread
3.2 隧道内压力变化幅值
测点压力由于所处位置的不同而有所不同。在头、尾车曲率变化较大处,测点压力幅值变化比较大。图9所示为列车头部不同位置测点的压力变化曲线。由图9可以看出:头车鼻尖(1号测点)压力幅值及压力峰峰值(最大、最小值之差)最大,最大压力幅值、峰峰值分别为5 466 Pa和2 968 Pa;而同一时刻,头车鼻尖与侧窗处压力之差可达5 kPa左右。列车中部几何结构相对简单,测点压力变化较小。图10所示为2号车中部3个不同高度测点的压力变化曲线。由图10可以看出:对于列车中部,随着车体垂向高度的不同,车身测点压力变化不大,压力幅值及压力峰峰值仅相差100 Pa左右。另外,虽然列车运行隧道为双向隧道,但车体两侧对称测点压力具有较好的一致性,幅值波动在50 Pa以内。
由于马赫波传播到测点的时刻不同,相比于车身垂向高度,车身测点纵向位置的不同带来的影响更大。基于本次分析采用的列车为8节编组,选取每节车体中部同一高度测点进行比对,如图11所示。由图11可见:随着测点位置从头车向尾车转变,测点压力的压力波形也逐渐发生改变:最大压力幅值逐渐减小,尾车中部测点最大压力已变为负值;而最小压力幅值逐渐增大,尾车比头车增加了483 Pa;测点压力峰峰值变化不大,波动在100 Pa左右。
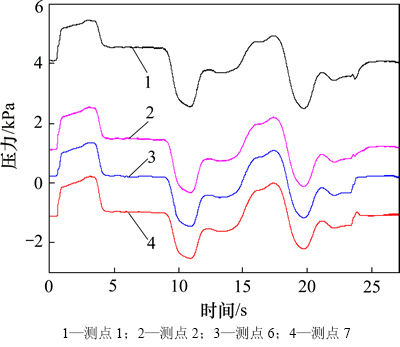
图9 车头不同位置测点压力变化曲线
Fig. 9 Curves of pressure for measured points of different locations on head surface
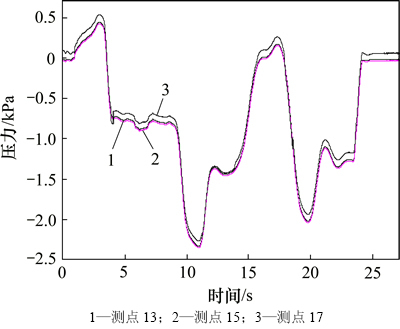
图10 车体中部不同高度测点压力变化曲线
Fig. 10 Curves of pressure for measured points of different heights on the middle of train
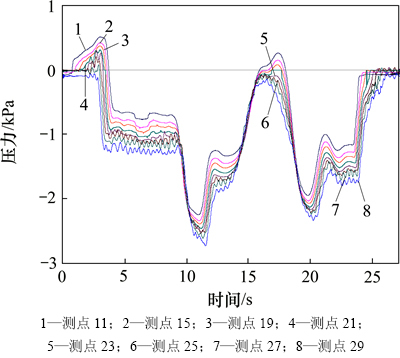
图11 车体中部不同纵向位置测点压力变化曲线
Fig. 11 Curves of pressure for measured points of different longitudinal locations on the middle part of train
相对于车体表面测点来说,隧道壁面上不同测点的压力变化更为复杂,测点压力峰峰值随隧道纵向位置的变化而改变。具体来说,在隧道的入口和出口处,测点压力峰峰值相对较小,而隧道中部测点压力峰峰值相对较大。以距轨面4.5 m高且靠近列车一侧的隧道壁面为例,离隧道口25,310,640,1 492和1 872 m处对应的测点压力峰峰值分别为2 470,3 111,4 232,3 847和2 167 Pa。图12所示为上述测点的压力波形曲线,由于受到隧道内马赫波传播及动车组通过时产生的双重影响,不同测点的压力曲线表现出很大的差异。
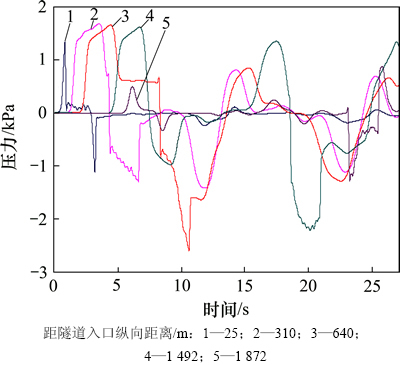
图12 隧道壁面不同纵向位置测点压力变化曲线
Fig. 12 Curves of pressure for measured points of different longitudinal locations on tunnel
对于隧道内同一截面,位于对称位置的测点压力变化基本相同,靠近车体侧壁面压力峰峰值略大,压力差不超过50 Pa;处于不同高度的测点压力在隧道入口处压力差较大,而在隧道中部压力差较小。以距轨面1.3 m和4.5 m这2个高度的测点压力为考察对象,距隧道入口25 m处,测点压力峰峰值相差27.3%;而在距隧道入口100 m后,测点压力峰峰值相差在10%以内。
4 有、无套衬结构隧道内气动效应对比
马赫波在隧道内传播时,若遇到截面的变化,会发生反射以及波形能量的变化[18]。例如当压缩波遇到截面缩小时,向前继续传播的波形幅值会增大,同时在截面缩小处会反射一个压缩波;相应的,当压缩波遇到截面扩大时,波形幅值会减小,而在截面扩大处反射一个膨胀波。
图13所示为隧道内有、无套衬时,车体表面中部测点瞬变压力变化曲线对比。当列车刚驶入隧道时,车头产生的压缩波传递到套衬开始端时,即遇到隧道截面变小,反射回来的压缩波传递到列车表面,使得车体表面压力升高(对应图13中A处);在套衬中继续传播的压缩波到达套衬结束端时,隧道截面开始扩大,又会向列车方向反射一股膨胀波,使得车体表面压力下降(对应图13中B处);同样的,对于车尾进入隧道时所产生的膨胀波,以及在隧道端口反射的马赫波,在每次经过套衬段时,都会发生相应的幅值变化和反射,再加上列车通过套衬段所产生新马赫波的叠加作用,使得加装套衬结构后的隧道气动效应更加复杂。
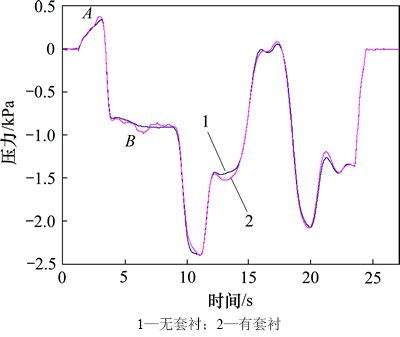
图13 车体表面测点压力曲线对比
Fig. 13 Comparison of pressure for measured point on train
然而,马赫波的转变及反射受截面比(下游段截面积/上游段截面积)影响很大。截面比越接近于1,马赫波幅值变化及反射的马赫波幅值就越小。对于隧道内加装厚度0.3 m套衬,套衬起始端与结束端的截面比分别为92.9%和107.6%,与1比较接近,因此使得马赫波每次经过套衬时,幅值改变很小且反射波幅值亦很小;另外,对于这样的截面比,在列车通过套衬时所产生的新马赫波幅值也非常小,所以套衬安装对于压力的波动影响并不明显。图14和图15所示分别为隧道内有、无套衬时,列车表面和隧道壁面不同测点的压力幅值及峰峰值对比。由图14和图15可以看出:加装厚度0.3 m套衬段前后,列车表面及隧道壁面测点压力会发生一定波动,但是波动较小,幅值差在2%以内。
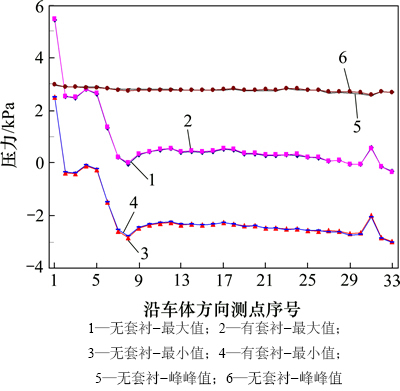
图14 车体表面测点压力峰值对比
Fig. 14 Comparison of peak values of pressure for measured points on train
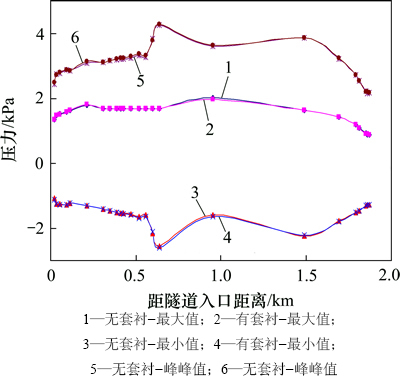
图15 隧道壁面测点压力峰值对比
Fig. 15 Comparison of peak values of pressure for measured points on tunnel
5 结论
1) 由数值模拟与动模型实验2种方法得到的结果较吻合。这2种方法得到的压力曲线变化规律完全一致,幅值误差在5%以内,说明本文采用的数值计算方法能够较好地模拟高速列车通过隧道时所诱发的空气动力效应问题。
2) 列车300 km/h通过双线隧道时,车身压力最大幅值及最大峰峰值发生在车头鼻尖处,且在车体头、尾部不同位置测点压力差别较大,头车鼻尖处压力比侧窗处大5 kPa左右;车体中部不同测点压力差别较小,同一截面上不同侧点压力幅值相差100 Pa左右,同一高度不同纵向测点压力幅值相差500 Pa以内。
3) 隧道壁面测点压力在隧道口附近峰峰值较小,但三维效应较强,不同高度测点压力峰峰值相差可达27.3%;靠近隧道中部,三维效应减弱,而壁面测点压力峰峰值较大。
4) 对于300 km/h高速列车,在现有位置(距隧道入口1/4处)安装套衬结构对于隧道内气动效应影响较小;安装套衬前后,车体表面及隧道壁面压力幅值变化在2%以内。因此,建议在对高速铁路双线隧道病害进行整治时,可以考虑采用套衬技术进行处理。
参考文献:
[1] 裴涛涛, 陈礼伟, 史宪明, 等. 既有铁路隧道衬砌裂损整治措施研究[J]. 铁道建筑, 2013(4): 76-79.
PEI Taotao, CHEN Liwei, SHI Xianming, et al. Study on treatment measures of cracks in lining of existing railway tunnel[J]. Railway Engineering, 2013(4): 76-79.
[2] 吴治家. 套衬技术在隧道病害整治工程中的应用[J]. 铁道建筑技术, 2011(5): 31-33.
WU Zhijia. The application of increasing lining in tunnel disease regulation project[J]. Railway Construction Technology, 2011(5): 31-33.
[3] Yamamoto A. Aerodynamics of a train and tunnel[C]// Proceedings of 1st International Conference on Vehicle Mechanics. Detroit: Society of Automotive Engineers, Inc, 1968: 151-163.
[4] Howe M S, Iida M, Fukuda T. Influence of an unvented tunnel entrance hood on the compression wave generated by a high-speed train[J]. Journal of Fluids and Structures, 2003, 17(6): 833-853.
[5] Howe M S. On the design of a tunnel-entrance hood with multiple windows[J]. Journal of Sound and Vibration, 2004, 273(1/2): 233-248.
[6] Howe M S, Iida M, Maeda T, et al. Rapid calculation of the compression wave generated by a train entering a tunnel with a vented hood[J]. Journal of Sound and Vibration, 2006, 297(1/2): 267-292.
[7] 骆建军, 高波, 王英学, 等. 高速列车穿越隧道的二维非定常流数值模拟[J]. 铁道学报, 2003, 25(2): 68-73.
LUO Jianjun, GAO Bo, WANG Yingxue, et al. Numerical simulation on an unsteady two-dimension flow produced by high-speed train passing a tunnel[J]. Journal of the China Railway Society, 2003, 25(2): 68-73.
[8] 骆建军, 高波, 王英学, 等. 高速列车通过隧道时压力变化的数值模拟[J]. 中国铁道科学, 2003, 24(4): 82-86.
LUO Jianjun, GAO Bo, WANG Yingxue, et al. Numerical study on the pressure change when high-speed train passing through a Tunnel[J]. China Railway Science, 2003, 24(4): 82-86.
[9] 赵文成, 高波, 王英学, 等. 高速列车突入隧道引起的压缩波的理论研究[J]. 西南交通大学学报, 2004, 39(4): 447-450.
ZHAO Wencheng, GAO Bo, WANG Yingxue, et al. Theoretical investigation of compression wave induced by high-speed train entering tunnel[J]. Journal of Southwest Jiaotong University, 2004, 39(4): 447-450.
[10] 赵文成, 高波, 王英学, 等. 喇叭型隧道入口的空气动力学特性的试验研究[J]. 四川大学学报(工程科学版), 2004, 36(4): 22-25.
ZHAO Wencheng, GAO Bo, WANG Yingxue, et al. Experimental investigation of aerodynamic characteristic of tunnel flaring portals[J]. Journal of Sichuan University (Engineering Science Edition), 2004, 36(4): 22-25.
[11] 马伟斌, 张千里, 刘艳青. 中国高速铁路隧道气动效应研究进展[J]. 交通运输工程学报, 2012, 12(4): 25-32.
MA Weibin, ZHANG Qianli, LIU Yanqing. Study evolvement of high-speed railway tunnel aerodynamic effect in China[J]. Journal of Traffic and Transportation Engineering, 2012, 12(4): 25-32.
[12] 王英学, 高波. 高速列车进出隧道空气动力学研究的新进展[J]. 中国铁道科学, 2003, 24(2): 83-88.
WANG Yingxue, GAO Bo. New development of the aerodynamics of high speed trains passing and out tunnels[J]. China Railway Science, 2003, 24(2): 83-88.
[13] 肖京平, 黄志祥, 陈立. 高速列车空气动力学研究技术综述[J]. 力学与实践, 2013, 35(2): 1-10.
XIAO Jingping, HUANG Zhixiang, CHEN Li. Review of aerodynamic investigations for high speed train[J]. Mechanics in Engineering, 2013, 35(2): 1-10.
[14] 王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004: 210-215.
WANG Fujun. Analysis of computational fluid dynamics[M]. Beijing: Tsinghua University Press, 2004: 210-215.
[15] 田红旗. 列车空气动力学[M]. 北京: 中国铁道出版社, 2007: 99-101.
TIAN Hongqi. Train aerodynamics[M]. Beijing: China Railway Press, 2007: 99-101.
[16] 田红旗. 中国列车空气动力学研究进展[J]. 交通运输工程学报, 2006, 6(1): 1-9.
TIAN Hongqi. Study evolvement of train aerodynamics in China[J]. Journal of Traffic and Transportation Engineering, 2006, 6(1): 1-9.
[17] 张雷, 田红旗, 杨明智, 等. 帽檐斜切式洞门斜率对隧道气动性能的影响[J]. 中南大学学报(自然科学版), 2013, 44(2): 817-822.
ZHANG Lei, TIAN Hongqi, YANG Mingzhi, et al. Influence on tunnel aerodynamic effects by slope of hat oblique tunnel portal[J]. Journal of Central South University (Science and Technology), 2013, 44(2): 817-822.
[18] Baron A, Mossi M, Sibilla S. The alleviation of the aerodynamic drag and wave effects of high-speed trains in very long tunnels[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(5): 365-401.
(编辑 杨幼平)
收稿日期:2014-11-04;修回日期:2015-02-27
基金项目(Foundation item):中南大学研究生自主探索创新项目(2014zzts038);高速铁路基础研究联合基金重点资助项目(U1334205);中国铁路总公司科技研究开发计划项目(2013B001-A-2);中南大学教师研究基金资助项目(2013JSJJ014) (Project(2014zzts038) supported by Exploration and Innovation Funds for Master Graduate Students of Central South University, China; Project(U1334205) supported by Joint Fund of High-speed Railway Fundamental Research, China; Project(2013B001-A-2) supported by Science and Technology Research Program of China Railway Corporation; Project(2013JSJJ014) supported by Teachers Research Fund of Central South University, China)
通信作者:姚松,副教授,从事轨道交通安全研究;E-mail: song_yao@csu.edu.cn