文章编号: 1004-0609(2005)07-1100-07

铝铸轧流场有限元模拟计算方案合理性的探讨

周英, 黄明辉, 钟掘

(中南大学 机电工程学院, 长沙 410083)

摘 要: 研究了铝铸轧的前箱及铸嘴型腔的流场的有限元分析的计算标准; 采用通用有限元计算软件ANSYS的FLOTRAN模块对型腔流场进行模拟计算; 对计算结果运用ANSYS自带的后处理技术及使用MATLAB软件对结果数据进行了处理, 比较了两种模拟工况的流场模型的出口速度线图, 并参照两次现场实验的现象及数据, 定量讨论了流场有限元计算的出口速度的绝对误差、 相对误差, 及其与出板速度、 出口开口度大小等因素的关系。 总结了流场有限元计算的许用不均匀度, 即稳定生产所要求的流场波动限度的标准的取值范围及其适用条件, 为未来有限元分析计算确定了初步依据。

关键词: 铸轧; 流场; 有限元分析; 许用不均匀度 中图分类号: TG331

文献标识码: A

Rationality of FEA model in fluid fields of aluminum roll-casting

ZHOU Ying, HUANG Ming-hui, ZHONG Jue

(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

Abstract: To explore the computation standards for finite element analysis of the fluid fields of the front-box and the nozzle-shaped space of aluminum roll-casting, the computation was performed by using the FLOTRAN module of the general finite element analysis software ANSYS. Postprocessing by ANSYS and stricter analysis of results by software MATLAB was reviewed. The allowable inhomogeneity and its applicabilities for fluid field finite element analysis have been rendered down from observations and recorded data of two experiments in reality. The primary standard of finite element analysis will be enriched by the developing technique of experiments and software.

Key words: roll cast; fluid field; finite element analysis; allowable inhomogeneity

材料铸轧成型技术利用材料从液态—半固态—固态的转变过程, 制备一定板型与厚度的板带材料。 对铝铸轧工艺的探索和研究一直是制造行业的重要任务。

铸轧生产工艺过程的影响因素较多, 其中的要素有: 铸嘴内铝熔体的流场及温度场分布、 轧辊辊套材质、 辊面温度及润滑等状况、 铸轧生产工艺参数(辊缝、 轧制力、 出板速度的匹配)等; 另外, 环境温度和湿度, 附属设施状况等因素也很重要。 诸多环节需和谐调控, 才能保证铸轧生产的稳定及实验的成功。 而铸嘴内部流场的分布, 是整个生产的关键环节^{[1, 2]}, 如果流场分布不合理, 即使保证了其他参数的合理, 要得到好的实验结果也很困难, 尤其在铝板厚度减薄的实验中, 对流场分布不均匀性更为敏感, 因此必须对流场作深入研究。

在铸嘴流场设计方面, 合理的过程是: 在实际实验之前, 先在计算机上模拟出铸嘴型腔内铝熔体的流动状况, 分析比较不同方案下的出口结果, 从而筛选出流场状况最好的方案, 再投入现场实验^[3-9]。 从理论上说, 流场应当尽可能地均匀分布, 但由于现场条件的制约, 无法完全实现理想分布状况的流场, 只能在保证正常生产的条件下, 尽量实现分布均匀, 容许一定程度上的流场分布不均匀, 因此就存在着一些问题, 如: 许用的出口流场不均匀度应当限制在何等范围? 然而, 由于实验手段和条件的限制, 至今尚未形成严格、 量化的流场设计的指导标准, 设计人员只能通过经验来衡量模拟方案的优劣, 导致理论与实践有所脱节。 在以往常规铸轧的铸嘴分析设计中, 因常规铸轧板速低, 板厚较大, 系统稳定性的容许度大, 对流场设计的要求不高, 即使是大型的铸嘴, 也只要能够合适地分流就能满足生产使用了。 但当铸轧速度提高^[10], 板厚减薄以后, 流场不均匀度的影响就会体现得非常明显, 这也是许多常规铸轧适用的铸嘴型腔在超薄快速铸轧的情况下却无法满足需要的原因。 因此, 研究探讨铸轧流场有限元分析标准, 对研究超薄快速铸轧的设计分析将是一个重要理论支柱。 国外虽然出现了设计流场的有关专利^[11], 但有关探讨流场设计标准的文献尚未见报道。 为此, 急需制订出模拟方案的评价标准, 以便有效指导流场模拟方案的设计。

本文作者运用有限元技术, 对铸轧实验的铸嘴内部铝熔体的流场进行了模拟分析, 并结合两次近期现场实验的现象和数据, 总结了流场模拟计算的暂行标准。 由于客观实验条件有限, 本结论只宜看作是初步的、 探索性质的, 还需要在未来的实验研究中不断修改完善。

1 有限元模型的建立

根据现场模型的前箱及铸嘴型腔的几何尺寸, 按照1∶1的比例建立了单分流块A模型和双分流块B模型。

1.1 边界条件

实验中该模型的边界条件设置如下。

进口 采用速度驱动, 施加进口速度矢量, 其大小根据出板速度折算平均施加在进口面上, A模型的出板速度为0.0165m/s, B模型的出板速度为0.0192m/s。

自由边界条件 针对前箱液位所在水平面, 限定速度矢量的v_z分量为0。

固定边界条件 施加的速度为0。 图1中除进口、 出口、 以及顶上的自由边界条件之外的面皆为固定边界条件, A模型和B模型的分流块所处的铸嘴型腔中的位置属于固定边界条件。

出口 压力为0。

边界条件设置示意见图1。

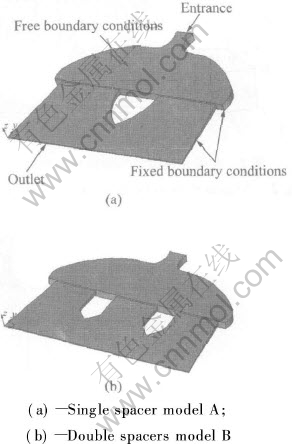
图1  有限元模型边界条件示意图

Fig.1  Schematic of boundary conditions of FEA model

1.2 网格划分

网格划分采用六面体映射网格(图2), 这是ANSYS流场计算推荐的网格形式。 映射网格的划分难度较大, 增加了流场计算的工作量, 但可以帮助求解稳定和获得更为精确的结果^[12]。 图2(a)所示为单个六面体映射网格的结构, 图2(b)所示为A模型中网格划分的局部示意图。

2 结果与分析

在流场中间平面即z=0平面的位置上, 因出口速度在此平面为最大, 朝z上下两边递减(图3所示为双块B模型的出口平面上节点的v_y速度的分布曲线图), 所以选取中间平面作为工作平面, 本文重点讨论其流场速度分布及出口部位的速度分布。

由于出口速度在3个坐标方向上的分量中, v_y与合速度同一个数量级, v_x(10^-1~10^-5倍于合速度)及v_z(10^-5~10^-11倍于合速度)均远小于该数量级, 因此选取了v_y作为主要研究对象, 讨论了其分布规律特点。

图2  有限元模型的六面体映射网格

Fig.2  Mapped hexahedral meshes of FEA

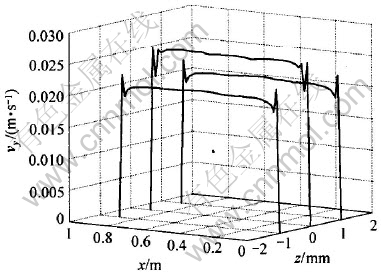
图3  模型B的出口即y=0面上节点的v_y分布示意图

Fig.3  Display of v_y of nodes at outlet on y=0 of model B

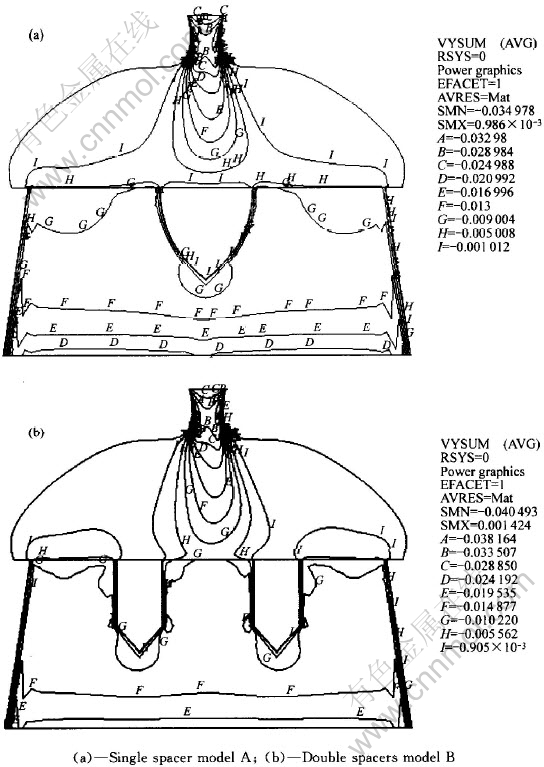
图4  中间平面上v_y分布的等值线图

Fig.4  Iso-surface display of v_y on middle plane

中间平面上A、 B模型的v_y速度分布等值线图见图4。 由于y坐标选取逆着出板方向为正, 因此出口计算值均为负, 图3中的数据已经去掉了负号, 图4中保留了原有计算数据, 负号仅说明v_y方向是沿出板方向。

中间平面上出口中线上v_y分布曲线及其平均值线见图5(数值已经去掉了负号)。 由于两个边部(每个单边约占总长的7%)的凝固条件比较好, 即使存在突变点, 也因冷却及时而不容易导致铸轧缺陷的出现, 因此重点分析了占总长86%的中段部位的计算结果。 根据现场情况分析, 容易发生缺陷的部位是与分流块的尾端位置相对应的, 因此单块A模型的突变点集中在正中, 双块B模型的突变点与分流块位置对应为两个。

图5  出口中线(y=0, z=0)上v_y的分布

Fig.5  Distribution of v_y at middle line of outlet (y=0, z=0)

从图5看出, A模型的中间突变比较大, 因此选取中点凹陷及其附近2高点讨论。 模拟计算了提速为0.025m/s时B模型的出口速度, 数据结果见表1。

另外, 沿z方向将v_y累加得到的是与流量成正比的数值, 其沿x方向的分布见图6。

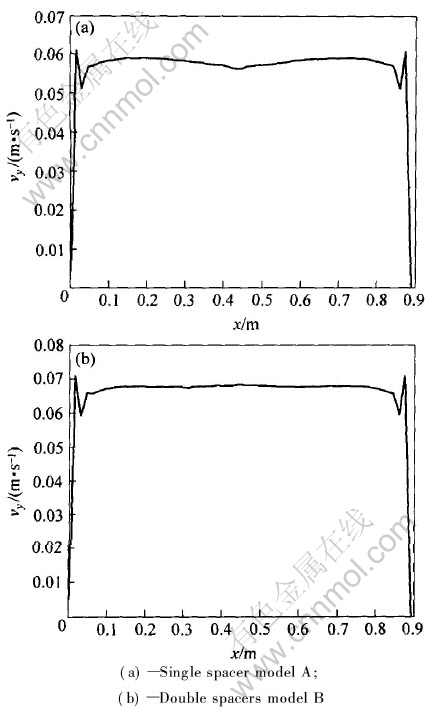
图6  出口面(y=0)沿z向累加的∑v_y沿x方向的分布

Fig.6  Distribution of sum of v_y along z axis at outlet (y=0)

3 现场实验现象

第一次实验采用B模型双分流块方案, 出口板宽沿x坐标方向, 根据两个突变点的位置, 可以将出口划分成: x坐标分别为0~0.325m(靠近驱动侧)、 0.325~0.565m(中段)和0.565~0.89m(靠近操作侧)3段。

实验开始时, 以0.0192m/s的速度立板, 调整稳定一段时间后开始提速, 在速度为0.025m/s时, 靠近驱动侧的一段首先发生堵死现象, 不再出铝, 接着操作侧的一段也发生了堵死现象, 仅剩下板宽方向中部约0.325~0.565m范围的部分继续出板, 板型破坏, 于是实验中断。

表1 两个模型的出口中线上v_y的结果分析

Table 1  Analysis of v_y at middle line of outlets of two models

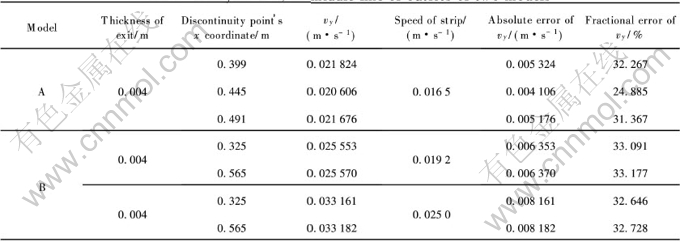
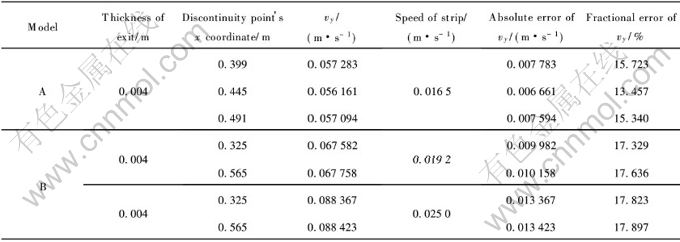
表2  两个模型的出口面(y=0)上在z向累加的∑v_y沿x方向分布

Table  Distribution of sum of v_y along z axis at outlets of two models

经过现场总结分析, 重新修订了实验方案, 采用了模拟计算以及现场经验一致认可的A模型单分流块方案进行了第二次实验, 采用0.0165m/s的立板速度, 该次实验出板完整, 但因设备因素终止了实验。

两个模型的出口近似流量(以沿z向的节点v_y累加之和∑v_y来代表, 如果将∑v_y与出口的微元面积相乘, 就是流量)分布示意图。

4 不均匀度的标准探讨

从结果分析来看, 不均匀度的选取与以下因素有关。

1) 分流块的形状和位置 流线型的分流块能够对分流起到更好的作用, 减少流动的阻力和应力集中; 在位置的选取上, 由于轧辊的构造特点, 出板靠近两侧边沿的冷却效果比中部更好, 因此即使边部流场计算出来并不均衡, 实际中也不容易在边部发生破坏, 因此选取位于铸嘴中部的单个分流块的A模型, 比起双块的B模型, 向两侧分流的效果更好。

2) 出口中线上v_y的绝对误差 A模型的绝对误差较小, 但考虑到A模型实验时的出板速度也较B模型的小, 因此单从该因素上, 看不出太大关系。

3) 出口中线上v_y的相对误差 相对于出口面上的流动平均速度来说, 整体误差越小越好。 但由于结构的限制, 存在着与分流块结构相关的几个特殊位置的突变点, 最容易导致铸轧板面出现不均衡状况。 结合发生了堵死现象的有限元模型来看, 相对误差超过30%~33%就会很容易发生铸轧不均衡的现象—要么堵死, 要么出现热带不凝固。 也就是说, 出口速度的相对误差越大, 对系统稳定性的削弱就越大。

4) 出口面上近似流量分布(沿z向累加的∑v_y)与平均值的绝对误差与相对误差 从流量的分布来看, A模型显然在中部的流量偏小, 而B模型的中部流量(在x为0.325~0.565范围)比两边略大, 这也说明了实际实验中两侧易冷凝堵死的原因。

5) 出板速度 同样模型条件下, 出口平均速度越大, 出口速度中线上v_y相对误差就会越小, 但出口面上流量的相对误差会加大, 因此, 适当情况下, 提速有助于生产的稳定, 但必须综合考虑并权衡流量的分析。

6) 板厚(辊缝厚度) 根据经验, 该因素亦影响出板的速度的相对误差。 具体影响程度还需要通过进一步的分析来判断。

7) 辊面冷却能力状况 该因素制约了流场的设计, 由于两个边部散热能力比中间相对要好, 因此在稳定运转以后, 中间部位的冷却能力要稍逊于两边, 因此, 中部出板位置的流速偏低为宜(参照模型a)。

综合以上分析得出的流场设计准则如下(铸轧流场计算的出口中部86%(撇开边部节点)范围内的节点应保证)。

1) 沿出板方向的分速度v_y相对误差许用值一般来说不能大于30%, 绝对误差不大于0.008m/s。 相邻节点的误差也应该是越小越好。 针对突变点(该点速度的量值一般来说比周围节点的要小)位置不同, 该误差也有所调整, 突变点位于中心时, 有利于铸轧稳定, 因此相邻节点的误差标准可以适当放宽(如本例中的A模型中部突变点与其相邻节点误差超过了6%, 但铸轧仍然是稳定的)。 只是可能会对板厚产生不利的影响, 因为不均衡性既然不能完全从出板y方向释放的话, 最有可能是向板厚z方向释放, 即厚度大的部位对应瞬时流量大的节点。

2) 沿出板x方向的流量分布相对误差应小于17%, 应尽量使正中部位略小于其两边流量分布的原则。 以上推断都是建立在稳定铸轧已经建立的情形下的局部变化, 如果稳定铸轧还未建立, 则上述推论无效。

由于实验条件的限制, 目前只进行了为数不多的铸轧提速实验, 尽管仍能从中获取重要信息, 但对总结规律还是有所影响, 而且铸轧又是一个需要多方面因素调控的工业生产过程, 因此除了理论的深入研究以外, 也要尽量多创造工业实验的机会。 本文对流场出口速度许用不均匀度的探讨还属初步, 将结合未来实验的发展, 在结合铸嘴内铝熔体的热分析^[13-15]之后作更多的拓展。

REFERENCES

[1]刘晓波, 毛大恒, 钟掘. 铝铸轧铸嘴分流块对型腔流场影响的研究[J]. 轻合金加工技术, 2000, 28(10):18-21.

LIU Xiao-bo, MAO Da-heng, Zhong Jue. Effect of nozzle spacer for roll strip casting on cavity fluid field[J]. Light Alloy Fabrication Technology, 2000, 28(10):18-21.

[2]周英, 钟掘, 吴鹿鸣, 等. 铸嘴型腔形状对型腔流场影响的二维有限元分析[J]. 机械, 2003, 30(5): 7-9.

ZHOU Ying, ZHONG Jue, WU Lu-ming, et al. Two-dimensional FEA of the influence of the shape of nozzle cavity on cavity fluid field[J]. Machinery, 2003, 30(5): 7-9.

[3]康志成. 铝连续铸轧铸嘴流场实验研究及理论建模[D]. 长沙: 中南大学机电工程学院, 2001.

KANG Zhi-cheng. Experiment studied and mathematical model of roll casting strip casting of Aluminum[D]. Changsha: School of Mechanical and Electrical Engineering, Central South University, 2001.

[4]邱竹贤. 铝冶金物理化学[M]. 上海: 上海科学技术出版社, 1985: 59.

QIU Zhu-xian. Physical chemistry of Aluminum metallurgy[M]. Shanghai: Shanghai Science and Technology Publishing Company, 1985: 59.

[5]Kang C G, Kim Y D. Model experiments for the determination of the heat-transfer coefficient and transition thermal analysis in the direct rolling process[J]. Journal of Materials Processing Technology, 1998, 84: 210-224.

[6]Lamberti G, Titomanlio G, Brucato V. Measurement and modelling of the film casting process 1. Width distribution along draw direction[J]. Chemical Engineering Science, 2001, 56(20): 5749-5761.

[7]Amit S, Yogeshwar S. Modeling of fluid flow and heat transfer in twin-roll casting of aluminum alloys[J]. Materials Transactions, 2002, 43(2): 206-213.

[8]Manish G, Yogeshwar S. Mathematical modeling of fluid flow, heat transfer, and solidification in two-roll melt drag thin strip casting of steel[J]. ISIJ International, 2000, 40(2): 144-152.

[9]梁涛. 双辊铸轧辊套传热规律及热辊型的数值模拟研究[D]. 长沙: 中南大学机电工程学院, 2002.

LIANG Tao. Research on Numerical Simulation of Heat Transfer and Thermal Crowning of Roll Shell during Twin-roll Casting[D]. Changsha: School of Mechanical and Electrical Engineering, Central South University, 2002.

[10]Haga T. A high speed twin toll caster for aluminum alloy strip[J]. Journal of Materials Processing Technology, 2001, 113: 291-295.

[11]苏鸿英. 世界超薄高速铝板铸轧机开发现状及其在我国的未来市场[J]. 世界有色金属, 2000(9): 4-6.

SU Hong-ying. Current developments of aluminum roll-casting strip caster in the world and its future prospects in China[J]. World Nonferrous Metals, 2000(9): 4-6.

[12]周英, 黄明辉, 钟掘. 网格划分对铸嘴型腔流场有限元分析的影响[J]. 中南大学学报(自然科学版), 2004, 35(1): 75-79.

ZHOU Ying, HUANG Ming-hui, ZHONG Jue. Influence of mesh types in two-dimensional FEA analysis of the cavity fluid field of nozzle cavity[J]. Journal of Central South University (Natural Science), 2004, 35(1): 75-79.

[13]Saxena A, Sahai Y. Modeling of fluid flow and heat transfer in twin-roll casting of aluminum alloys[J]. Materials Transactions, 2002, 43(2): 206-13.

[14]Nastac L, Li B Q. Modeling of single-roll strip casting of Al-1%Mn alloy: correlation of strip thickness, solidification zone length and puddle shape[A]. Multiphase Phenomena and CFD Modeling and Simulation in Materials Processes Symposium[C]. Warrendale, PA, USA Publisher: TMS, 2004. 325-34.

[15]Huey-Jiuan Lin. Modelling of flow and heat transfer in metal feeding system used in twin roll casting[J]. Modelling and Simulation in Materials Science and Engineering, 2004, 12(2): 255-72.

基金项目: 国家重点基础研究发展规划资助项目(G1999064906)

收稿日期: 2004-12-17; 修订日期: 2005-04-04

作者简介: 周英(1972-), 女, 讲师, 博士研究生.

通讯作者: 周英, 博士研究生; 电话: 0731-2656775; E-mail: zhouying@csu.edu.cn

(编辑 龙怀中)