基于PSO算法的HVAC系统LSSVM预测控制
邹木春1,龙文2
(1. 宜春学院 数学与计算机学院,江西 宜春,336000;
2. 中南大学 信息科学与工程学院,湖南 长沙,410083)
摘要:针对暖通空调(HVAC)系统,提出一种基于粒子群优化(PSO)算法和最小二乘支持向量机(LSSVM)的预测控制方法。该方法利用LSSVM建立HVAC系统预测模型并预测系统的输出值,引入输出反馈和偏差校正以克服模型失配等因素引起的预测误差,以此构造加权预测控制性能指标。由PSO算法滚动优化得到系统的最优控制量。利用该控制方法对一个HVAC系统进行仿真实验,结果表明该方法具有较好的控制效果。
关键词:暖通空调系统;预测控制;最小二乘支持向量机;PSO算法
中图分类号:TP273 文献标志码:A 文章编号:1672-7207(2012)07-2642-06
LSSVM predictive control for HVAC system with PSO algorithm
ZOU Mu-chun1, LONG Wen2
(1. School of Mathematics and Computer, Yichun College, Yichun 336000, China;
2. School of Information Science and Engineering, Central South University, Changsha 410083, China)
Abstract: For the system of heating, ventilating and air-conditioning (HVAC), a nonlinear predictive control algorithm based on particle swarm optimization (PSO) and least square support vector machine (LSSVM) was proposed. It utilizes LSSVM to estimate the HVAC system model and forecast the output value, reducing the error in output feedback and error correction. A new weighted predictive control performance index is formulated. The optimal control values of the nonlinear system are obtained by the rolling optimization of PSO algorithm. An optimal control system is designed to control a HVAC system; simulation results show that the proposed nonlinear predictive control algorithm is effective.
Key words: heating ventilating and air-conditioning (HVAC) system; predictive control; least square support vector machine (LSSVM); PSO algorithm
暖通空调(HVAC)过程控制系统是一类强非线性、多耦合、大时滞和多输入多输出的典型对象,常用的控制方法是基于传统控制理论的方法,如PID控制等。当系统存在干扰时,难以获得令人满意的控制效果。预测控制是目前应用很成功的先进控制技术之一,它是一种基于预测模型、滚动优化和反馈校正的控制算法[1-2]。常用的预测模型有Hammerstein模型、Wiener模型和神经网络模型等。尽管神经网络可以逼近任意复杂的非线性函数、自适应能力强等优点,但仍存在网络拓扑结构难以确定、易陷入局部极小等问题。1999年,Suykens等[3]提出了最小二乘支持向量机(LSSVM)用于求解非线性函数的回归问题。LSSVM在支持向量机(SVM)的基础上用等式约束替代不等式约束,避免了求解耗时的二次规划问题,LSSVM可以以任意精度逼近非线性系统,是非线性系统建模的有力工具。因此,已有许多研究者将LSSVM应用于复杂工业过程建模和预测控制中,并取得了较好的结果[4-6]。另一方面,由于系统的预测模型是非线性的,求解控制量的滚动优化问题则是个非线性约束优化问题。粒子群算法(PSO)简单,容易实现,具有收敛速度快、全局寻优和处理约束的能力[7],能够满足滚动优化问题的实时性和精度高的要求,非常适用于求解非线性滚动优化问题。本文作者提出了一种基于PSO和LSSVM的非线性预测控制算法用于HVAC系统的控制。其主要思路为利用LSSVM建立HVAC系统的模型作为预测模型,在每个采样时刻,预测模型预测HVAC系统未来一个时刻的输出,用输出反馈进行偏差校正并得到关于偏差和控制量的优化目标,粒子群算法作为滚动优化策略来求解得到最优控制量。仿真实验结果表明该算法的有效性。
1 暖通空调系统
一个典型的暖通空调(HVAC)系统[8]如图1所示。它是由热交换器、循环风机、空调区域、连接管道系统、调节阀等组成。

图1 HVAC系统模型
Fig.1 HVAC system model block diagram
HVAC系统的工作原理为[8]:首先将经过处理的新风、回风的混合风送入风道,其中,混合风中回风占75%,新风占25%。混合风经过过滤器过滤后冷却、除湿,再由送风机送入室内,最后利用冷冻水循环水泵使冷冻水流经表面冷却器提供冷源。HVAC系统的数学模型[9]为




 (1)
(1)
式中:t3为室内温度;f为送风风速;Vs为房间体积;t2为送风温度;hfg为水蒸汽焓值;cp为空气比热容;w2为送风空气含湿量;w3为室内空气含湿量;ρ为空气密度;Q0为房间显热负荷;M0为房间湿负荷;Vhe为热交换器容积;t0为室外温度;hw为液态水焓值;w0为室外空气含湿量;gpm为冷水流量。式(1)所示的HVAC系统数学模型假设:(1) 气体是理想气体;(2) 气体充分混合;(3) 压力恒定;(4) 忽略各成分间的热量损失;(5) 忽略气体在分离和混合过程中的瞬时作用;(6) 忽略墙和房间的储热作用;(7) 忽略相互渗透和扩散作用。
2 PSO优化的HVAC系统LSSVM预测控制
2.1 LSSVM模型
非线性预测控制中预测模型的功能是根据对象的历史信息和未来输入预测其未来输出。预测模型是否能够反映对象的特征,直接关系到控制器的稳定性和精度,因此,研究有效的、高精度的预测模型是非模型预测控制要解决的关键问题。本文利用最小二乘支持向量机的优点建立LSSVM模型作为预测模型进行预测。
m个输入n个输出的有约束多变量非线性系统可表示为:
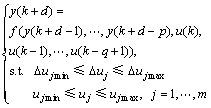 (2)
(2)
式中: ,
, 分别为第k时刻输入、输出向量;d为输出延迟;q,p分别为输入和输出的阶次,约束条件限定了控制量的范围和变化幅度。
分别为第k时刻输入、输出向量;d为输出延迟;q,p分别为输入和输出的阶次,约束条件限定了控制量的范围和变化幅度。
对N组数据 ,
,
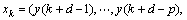
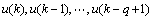
 ,i=1, 2, …, n
,i=1, 2, …, n
用非线性映射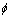 把样本从原空间映射到特征空间,特征空间中的LS-SVM估计模型的形式为
把样本从原空间映射到特征空间,特征空间中的LS-SVM估计模型的形式为 ,
, 为权重系数,b为偏置。寻找
为权重系数,b为偏置。寻找 和b,实际上是最小化
和b,实际上是最小化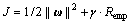 ,
,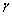 为正则化参数,
为正则化参数, 为损失函数。LS-SVM目标函数中选取损失函数为
为损失函数。LS-SVM目标函数中选取损失函数为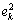 ,则有[9]
,则有[9]
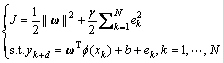 (3)
(3)
利用拉格朗日函数法求解上面的优化问题,定义核函数为 φT(xi)φ(xj),LS-SVM预测模型
φT(xi)φ(xj),LS-SVM预测模型
 φ
φ (4)
(4)
2.2 PSO优化的HVAC系统LSSVM预测控制器
对一个有d步延迟的系统,当输入为u(k)时,输出为y(k+d),利用系统过去的输入输出和当前u(k),由LSSVM预测模型可得到系统预测输出为 。对待优化的输入
。对待优化的输入 ,由预测模型可得到系统的预测输出为
,由预测模型可得到系统的预测输出为 。定义系统的实际输出和预测输出的偏差为:
。定义系统的实际输出和预测输出的偏差为:
 (5)
(5)
可得反馈校正后k+1时刻的预测输出为:
 (6)
(6)
非线性预测控制性能指标目标函数为:

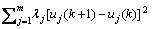 (7)
(7)
对于HVAC系统,基于PSO优化的LSSVM预测控制算法框图如图2所示。
非线性模型预测控制中滚动优化的基本思想是通过迭代算法在有限的预测步数内,搜索控制向量 ,使性能指标目标函数达到最小。本文采用基于动态惯性权重的粒子群算法进行滚动优化。针对非线性模型预测控制滚动优化目标函数(7)及约束条件,将控制域上的一组控制变量序列作为PSO要寻优的位置向量,各粒子的适应度函数取性能指标目标函数J,以目标函数最小为评价标准。
,使性能指标目标函数达到最小。本文采用基于动态惯性权重的粒子群算法进行滚动优化。针对非线性模型预测控制滚动优化目标函数(7)及约束条件,将控制域上的一组控制变量序列作为PSO要寻优的位置向量,各粒子的适应度函数取性能指标目标函数J,以目标函数最小为评价标准。

图2 PSO优化的HVAC系统LSSVM预测控制
Fig.2 LSSVM predictive control for HVAC system with PSO
在PSO算法中, 表示粒子i的位置向量,
表示粒子i的位置向量, 表示第i个粒子所经历过的最好位置,每个粒子的速度向量表示为
表示第i个粒子所经历过的最好位置,每个粒子的速度向量表示为 ,种群中所有粒子经历过的最好位置为
,种群中所有粒子经历过的最好位置为 ,粒子的速度、位置更新公式如下:
,粒子的速度、位置更新公式如下:
 (8)
(8)
式中:c1和c2为学习因子,为了保证PSO算法的收敛性,通常取c1=c2=1.494 45[10]。r1和r2为[0, 1]之间的随机数。w为惯性权重。w为粒子群算法的一个关键参数,它可以平衡算法的全局搜索能力和局部搜索能力,因此,本文采用动态惯性权重,即惯性权重w随进化代数线性递减:
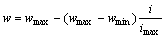 (9)
(9)
其中:i为当前迭代次数;imax为最大迭代次数。
2.3 算法步骤
对于HVAC系统,基于PSO优化的LSSVM预测控制(P-LSSVM-PC)算法步骤如下:
Step 1 设置PSO算法和LSSVM模型参数。
Step 2 根据HVAC系统的历史数据或对HVAC系统采样得到输入输出数据构成样本集。使用LS- SVM对训练样本进行训练,离线建立HVAC系统的LSSVM预测模型。
Step 3 用测试样本对HVAC系统LSSVM预测模型进行辨识,检查辨识误差是否在允许的范围内。如果辨识误差在允许的范围内,继续执行step 4;否则,改变LSSVM参数重新训练和辨识,直到辨识误差满足要求。
Step 4 在第k个时刻,对于控制量u(k),HVAC系统的输出为y(k+d),通过LSSVM预测模型得到k时刻的预测输出为 。设k+1时刻的控制量u(k+1)为待优化的量,把它作为PSO算法中粒子的位置向量,代人LSSVM预测模型中得到k+1时刻HVAC系统的预测输出
。设k+1时刻的控制量u(k+1)为待优化的量,把它作为PSO算法中粒子的位置向量,代人LSSVM预测模型中得到k+1时刻HVAC系统的预测输出 。
。
Step 5 由式(7)计算每个粒子的适应度,比较并更新粒子的历史最优pi和全局最优p g。
Step 6 按式(8)更新粒子的位置和速度。
Step 7 如果满足粒子群优化算法结束条件,输出最优控制量u(k+1),转step 8;否则转step 5。
Step 8 将控制量u(k+1)作用于HVAC系统进行控制。令k:=k+1,转向step 4直至控制结束。
3 仿真研究
文献[9]给出了典型的HVAC系统数学模型如式(1)所示。HVAC系统表现出强烈的非线性特性,系统的一些操作参数见表1。
HVAC系统控制的目标是它所提供的工作、生活环境达到舒适性要求的同时尽可能地节约能源消耗。根据Fanger提出的HVAC系统舒适性指标[11]和Betzaida提出的能耗指标[8],本文将送风风速f和冷水流量gpm分别作为输入u1=f,u2=gpm,将室内空气温度t3和室内空气相对湿度w3分别作为输出y1=t3,y2=w3,则该HVAC过程控制系统可看成一个两输入两输出的非线性系统。
表1 HVAC系统操作参数
Table 1 Operation parameters of HVAC system

为了求解方便,当采样周期较短时,本文采用数值逼近的方法把式(1)的微分方程转换成差分方程,为此可作如下近似
 (10)
(10)
其中:k为采样序号;t为采样周期。
针对上述HVAC系统,假设系统输出对输入的延迟d=0,选取u1(k)和u2(k)的均匀随机序列作为输入,通过求解式(11)所示的HVAC系统模型方程,得到300组数据组成形如[u1(k), u2(k), y1(k), y2(k), yi(k+1)], i=1, 2的2个样本集。考虑到LSSVM具有小样本学习能力,因此用来训练模型的样本数据不要太多,否则为后面的实时在线滚动优化增加负担。分别将2个样本集中200组数据训练建立2个输出T3和W3的 LSSVM预测模型,2个样本集中的另外100组数据用来对2个模型进行辨识。在建模过程中,选取径向基函数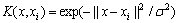 为核函数,核参数γ1=γ2=1 000,
为核函数,核参数γ1=γ2=1 000,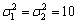 。PSO算法的参数设置为c1=2,c2=2,wmax=0.9,wmin=0.4,种群规模大小为20,最大迭代次数为100,权系数λj=0, j=1, …, m。采样周期为10 s。2个输出室内温度t3和室内相对湿度w3的LS-SVM模型辨识结果如图3和图4所示。
。PSO算法的参数设置为c1=2,c2=2,wmax=0.9,wmin=0.4,种群规模大小为20,最大迭代次数为100,权系数λj=0, j=1, …, m。采样周期为10 s。2个输出室内温度t3和室内相对湿度w3的LS-SVM模型辨识结果如图3和图4所示。
从图3和4可以看出:2个LSSVM预测模型的误差绝对值均在0~0.04之间,这表明2个模型具有较高的预测精度。
在仿真控制中,主要考察本文提出的基于PSO优化的HVAC系统LSSVM预测控制器的设定值跟踪能力。系统的参考轨迹设置为:假设在采样时刻0,室内温度的设定值为24 ℃,相对湿度的设定值为40%;在时刻20,温度的设定值从24 ℃跳变到26 ℃,相对湿度的设定值从40%跳变到60%; 在时刻40,温度的设定值从26 ℃跳变到28 ℃,而相对湿度从60%跳变到80%; 在时刻60,温度从28 ℃跳变到27 ℃,相对湿度从80%跳变到70%; 在时刻80,温度从27 ℃跳变到25 ℃,而相对湿度从70%跳变到50%。通过PSO优化的LS-SVM预测控制算法获得控制量,优化每个控制量的时间不超过0.78 s。算法P-LSSVM-PC与常规基于支持向量机的预测控制算法(SVM-PC)进行了比较,算法SVM-PC的参数设置与P-LSSVM-PC相同。系统跟踪室内温度、室内相对湿度设定值的控制效果比较如图5所示。
从图5可知:对于HVAC系统,当参考轨迹发生变化时,基于PSO优化的LSSVM预测控制算法(P-LSSVM-PC)能够及时地给出相应的控制量,使系统能够较好地跟踪室内温度和相对湿度的参考轨迹,而常规SVM-PC算法的控制效果相对较差。这说明对于非线性HVAC系统,本文提出的P-LSSVM-PC算法比常规SVM-PC算法具有更好的控制性能。

图3 温度LSSVM模型辨识结果
Fig.3 Identification results of LSSVM model with temperature

图4 相对湿度LSSVM模型辨识结果
Fig.4 Identification results of LSSVM model with relative humidity

图5 HVAC系统跟踪设定值曲线
Fig.5 Control simulation results of HVAC system
4 结论
针对多变量非线性HVAC系统,提出一种基于PSO优化的LSSVM预测控制算法。该方法构造HVAC系统预测控制框架,对HVAC系统预测控制只需要系统的输入输出数据建立LSSVM预测模型,而不要求已知HVAC系统的数学模型,利用PSO算法优化获得控制量。仿真实验结果表明该方法有效。
参考文献:
[1] Clarke D W, Mohtadi C, Tuffs P S. Generalized predictive control (part Ⅰ): The basic algorithm[J]. Automatica, 1987, 23(2): 137-148.
[2] 侯志祥, 吴义虎, 袁松贵, 等. 基于AEPSO优化的神经网络多步预测控制[J]. 中南大学学报: 自然科学版, 2007, 38(6): 1162-1168.
HOU Zhi-xiang, WU Yi-hu, YUAN Song-gui, et al. Multi-steps predictive control of neural networks based on AEPSO optimization[J]. Journal of Central South University: Science and Technology, 2007, 38(6): 1162-1168.
[3] Suykens J A K, Vandewalle J. Least squares support machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300.
[4] 张海鹰, 廖建勇. 基于最小二乘支持向量机的振动切削力软测量模型及其应用[J]. 中南大学学报: 自然科学版, 2010, 41(3): 982-987.
ZHANG Hai-ying, LIAO Jian-yong. A soft-sensing model on vibration cutting force based on least squares support vector machine and its application[J]. Journal of Central South University: Science and Technology, 2010, 41(3): 982-987.
[5] Esen H, Ozgen F, Esen M. Modeling of a new solar air heater through least squares support vector machines[J], Expert Systems with Applications, 2009, 36(7): 10673-10682.
[6] 郭振凯, 宋召青, 毛剑琴. 基于最小二乘支持向量机的非线性广义预测控制[J]. 控制与决策, 2009, 24(4): 520-525.
GUO Zhen-kai, SONG Zhao-qing, MAO Jian-qin. Nonlinear generalized predictive control based on least square support vector machine[J]. Control and Decision, 2009, 24(4): 520-525.
[7] Kennedy J, Eberhart R C. Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks. Perth, 1995: 1942-1948.
[8] Betzaida A S, Miguel V R. Nonlinear control of a heating, ventilating, and air conditioning system with thermal load estimation[J]. IEEE Transactions on Control Systems Technology, 1999, 7(1): 56-63.
[9] Sun C Y, Mu C X, Li X M. A weighted LSSVM approach for the identification of a class of nonlinear inverse systems[J]. Science in China Series F-Information Sciences, 2009, 52(5): 770-779.
[10] Clerc M. The swarm and the queen: towards a deterministic and adaptive particle swarm optimization[C]//Proceedings of IEEE Congress on Evolutionary Computation. New Jersey, 1999: 1951-1957.
[11] 魏东, 张明廉, 支谨. 神经网络非线性预测优化控制及仿真研究[J]. 系统仿真学报, 2005, 17(3): 697-700.
WEI Dong, ZHANG Ming-lian, ZHI Jin. Artificial neural network-based nonlinear predictive optimal control and simulation[J]. Journal of System Simulation, 2005, 17(3): 697-700.
(编辑 陈爱华)
收稿日期:2011-08-03;修回日期:2011-12-07
通信作者:邹木春(1970-),男,江西丰城人,副教授,硕士,从事优化算法、智能信息处理的研究;电话:15879552080;E-mail: zmclhj222@yahoo.com.cn