DOI: 10.11817/j.issn.1672-7207.2016.10.028

基于首超准则的随机车流下悬索桥加劲梁动力可靠度评估

肖新辉^{1, 2, 3}，鲁乃唯¹，刘扬¹，郭鑫³

 (1. 长沙理工大学 土木与建筑学院，湖南 长沙，410114；

2. 长沙理工大学 桥梁结构安全控制湖南省工程实验室，湖南 长沙，410114；

3. 长沙理工大学 交通科学研究院, 湖南 长沙，410114)

摘要：为了研究考虑车辆运行状态的大跨度悬索桥加劲梁动位移概率特征及桥梁运营期的安全水平，基于实测车流数据和动力可靠度理论分析悬索桥加劲梁在运营期内车致响应的动力可靠度。建立考虑车辆占有率的桥梁动力可靠度数学模型，分析主跨为820 m的悬索桥在运营期内稀疏运行车辆和密集运行车辆作用下的加劲梁位移动力可靠度。研究结果表明：在随机车流作用下，悬索桥加劲梁在1/4跨节点的位移动力响应均方根最大，且加劲梁位移的界限跨越率随车辆样本数量的增大趋于稳定；在100 a内，实际运行状态下的动力可靠指标由5.92降至5.11，介于密集运行状态与稀疏运行状态之间；在不考虑桥梁抗力退化的情况下，随机车流作用下悬索桥加劲梁位移超限失效事件主要由密集运行车辆引起，但随着密集运行车辆的增大，可靠指标下降趋势减缓。

关键词：桥梁工程；悬索桥；动力可靠度；随机车流；响应均方根

中图分类号：U448.25             文献标志码：A         文章编号：1672-7207(2016)10-3491-07

Dynamic reliability assessment for girders of suspension bridges under random traffic flow based on the first-passage criterion

XIAO Xinhui^{1, 2, 3}, LU Naiwei¹, LIU Yang¹, GUO Xin³

 (1. School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410114, China;

2. Hunan Province Engineering Laboratory of Bridge Structure,

Changsha University of Science and Technology, Changsha 410076, China;

3. Transportation Research Institute, Changsha University of Science and Technology, Changsha 410114, China)

Abstract: In order to analyze the probabilistic characteristics of dynamic responses and safety level of stiffening girders for long-span suspension bridges considering the actual vehicle states, the vehicle involving vibration and the dynamic reliability indices were studied based on the measured vehicle data and dynamic reliability theory. The mathematic models of dynamic reliability were established considering the proportion of heavy vehicles. The dynamic reliability of a suspension bridge with 820 m mid-span under spare and heavy vehicles loads were discussed. The results show that the root-mean-square of displacement responses reaches the peak value in 1/4 span of the suspension girders under random traffic flow. The boundary cross rates of dynamic responses are stable with the increase of random vehicle sample number. In 100 years, the dynamic reliability index will drop to 5.11 from 5.92 under the actual operational state, which is caused by heavy and spare operation. Without considering resistance deterioration of the bridge, the failure events of over-ranging displacement are caused by the existence of heavy traffic flow. The dynamic reliability slows down with the increase of the heavy vehicles.

Key words: bridge engineering; suspension bridge; dynamic reliability; random traffic flow; root-mean-square response

公路交通量和车辆超载率的逐渐增长致使桥梁在运营期的安全性有所降低。大跨度悬索桥整体刚度较低，车载下加劲梁将产生较大位移，位移过大将影响桥梁正常使用。车辆的车型和车质量等参数具有随机性，车载下桥梁的动力响应为随机过程，引入结构动力可靠度理论可研究车载下桥梁的安全水平。准确评估实际交通荷载下大跨度悬索桥加劲梁的动力可靠度具有重要意义。针对车载下桥梁的动力响应研究，王达等^[1]研究了随机车流下桥梁的动力响应特征，讨论了车辆模型及路面平整度对车桥系统振动的影响。韩万水等^[2]研究了风-汽车-桥梁的耦合振动响应，讨论了车辆运行状态对桥梁动力响应的影响。邓子铭等^[3]引入地震荷载作用至车桥耦合振动系统，研究了钢桁梁桥在地震荷载作用下的行车行驶安全性。上述研究针对桥梁动力响应进行了确定性分析，没有统计桥梁动力响应的概率特征，无法评估车载下桥梁的安全概率。XIANG等^[4]基于一次二阶矩法(FOSM)研究了考虑车桥耦合振动的简支梁桥动力可靠度，认为车辆的随机性比桥梁结构参数随机性影响更大。刘扬等^[5]基于体系可靠度理论对悬索桥加劲梁截面尺寸进行了优化设计。周剑波^[6]对随机车流作用下的连续刚构桥的动力可靠度研究仅限于对荷载效应进行统计分析，没有基于动力可靠度的跨越理论，实质上是静力可靠度研究范畴。为了使基于实际交通荷载评估大跨度悬索桥加劲梁达到正常使用安全水平，本文作者基于WIM (动态称质量系统)建立密集和稀疏状态下某悬索桥的随机车流模型，以便揭示车辆运行状态下加劲梁的位移响应均方根分布规律。建立界限跨越概率模型，并基于动力可靠度的位移首超准则讨论密集车辆占有率对加劲梁动力可靠度的影响。

1  车载下桥梁位移首超动力可靠度数学模型

车辆以一定的速度通过桥梁时对其产生动力效应，若超过若界限值，则影响桥梁正常使用或安全性能。车载下桥梁位移首超动力可靠度的数学模型需从车载下桥梁的位移响应和桥梁位移首超概率模型   引入。

针对车载下桥梁结构的动力响应，将车辆和桥系统耦合系统简化为车辆和桥梁2个子系统，分别建立其运动方程，由位移和力学平衡方程求解响应值。车桥系统的振动微分方程可表示为^[7]：

        (1)

        (2)

式中：M，C和K分别为质量矩阵、阻尼矩阵和刚度矩阵；下标v和b分别表示车辆和桥梁；F_vb和F_bv分别表示车-桥耦合振动的车辆与桥梁的1对相互作用力；F_vg和F_bg分别表示作用在车辆和桥梁上与车-桥耦合不相关的荷载列向量。可采用振型分解法和有限元模型方法等求解车-桥耦合振动方程。针对具有几何非线性的大跨度悬索桥，采用基于Ansys的有限元模型方法^[8]求解车载下桥梁的动力响应。

在得出车载下桥梁的动力响应时程后，将其转换为频域数据，基于随机振动原理，在频率范围求解动力响应均方根σ_Ｘ^[9]：

          (3)

式中：H(w)为频率响应函数；S(w)为荷载功率谱密度；当n=1时，σ_x为结构响应均方根值。结构参数与车辆荷载参数具有随机性，因此，σ_x是与荷载参数有关的随机变量^[10]。由于结构参数相对于车辆荷载的随机性较小，本文暂不考虑结构参数的随机性，仅考虑随机车辆荷载对结构动力可靠度的影响。

随机车辆荷载作用下桥梁的响应属于随机过程，因此，其失效准则和研究方法与传统的静力可靠度有所不同，基于动力可靠度理论可较好地研究桥梁结构的安全问题。目前，结构动力可靠度主要是基于首次超越破坏和疲劳损伤为基础进行研究。在失效准则方面，RICE^[11]最早基于首次超越准则建立了随机过程x(t)在时间T内与某一界限值b的交叉次数期望N_b(T)的表达式：

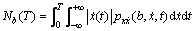       (4)

式中：为x(t)和的联合概率密度函数。式(4)的精确求解较困难，若随机激励为平稳随机过程，则可采用界限跨越率的方式求解。对式(4)求导可得到界限值b的跨越率v_b(t)为

           (5)

结合RICE^[11]给出的零均值的平稳正态随机响应的界限跨越率公式，并考虑车载下桥梁动力响应均值μ_x和可得车载下桥梁的界限跨越率公式为

       (6)

式中：和分别表示x(t)在界限值b的上、下跨越率。求解式(6)中的μ_x和σ_x成为车载下桥梁结构动力可靠度分析的关键。

结构动力可靠度的首超准则假定界限跨越次数概率分布服从Possion分布和Markov分布。文献[1]证明了当界限值b较大时2个假定的可靠度计算结果相同。在时间T内，基于Poisson假定的结构失效概率为^[12]

       (7)

引入随机车流模型，根据车距将车辆划分为稀疏运行状态和密集运行状态。假定稀疏运行状态下的界限跨越率为v_b1，车辆占有率为a₁；密集运行状态下界限跨越率为v_b2，车辆占有率为a₂。一般运营态(综合考虑稀疏运行状态和密集运行状态)下桥梁首超准则的失效概率为

      (8)

式(8)为车载下桥梁位移首超动力可靠度数学模型。数学模型的求解采用以下思路：首先，基于有限元求解随机车流下桥梁的位移响应时程数据；其次，将时程数据转换为频域数据并进行频谱分析；最后求解位移首超动力可靠度。具体求解流程如图1所示。

图1  车辆荷载作用下桥梁的动力可靠度分析流程

Fig. 1  Flow chart for dynamic reliability analysis of bridges under vehicle loads

图1中，车辆模型可采用ANSYS有限元中的MASS21单元模拟，通过COMBIN12弹簧单元将其与桥梁单元连接。FFT函数为MATLAB中的fast Fourier Transform(快速傅里叶变换)函数。图1所示的流程图采用响应频谱分析的方法将随机车流的时域数据转换为动可靠度分析所需的频域数据，较好地解决了随机车流作用下结构时程响应与动力可靠度分析所需概率特征值问题。

2  随机车流下悬索桥加劲梁位移统计分析

2.1  工程背景与有限元模型

南溪长江大桥是宜泸渝高速公路上主跨L=820 m的单跨钢箱梁悬索桥，桥型布置图如图2所示。主缆横桥向中心间距为29.1 m，钢箱梁共65片，标准长度为12.8 m。南塔和北塔各设1对竖向支座、1对横向抗风支座和1对纵向阻尼装置。

图2  南溪长江大桥桥型布置图

Fig. 2  Overall layout of Nanxi Yangtze river bridge

采用ANSYS软件建立南溪长江大桥的脊骨梁模型。索塔和加劲梁为BEAM4梁单元，主缆和吊杆为LINK8杆单元，二期恒载采用MASS21单元模拟。

文献[13]基于健康监测数据研究了润扬长江大桥的动力特性，研究表明该桥实测振型与设计结构有一定差异。根据文献[14]采用的有限元模型更新方法，结合实桥健康监测系统的劲梁模态，更新本有限元模型的主缆初张力等参数。有限元模型更新后的竖向模态和实测模态如表1所示。

表1  竖向模态的计算值与实测值

Table 1  Calculation values and measured values of vertical modes

2.2  随机车流模拟

为了区分稀疏运行状态和密集运行状态车辆，建立车辆的时域模型。在时域内生成随机车流的步骤如下：首先，基于WIM(动态称重系统)对行车流量进行监测的数据建立随机车流数据库；然后，对数据库的随机参数进行统计分析；最后，在MATLAB平台采用Monte Carlo抽样生成随机车流样本。

随机车辆主要有车型、车速、质量和行车间距4个随机参数。车型一般服从均匀分布。针对宜泸渝调整公路车辆监测数据，将车型分为C1(小型客车)、C2(双轴货车)、C3(三轴货车)、C4(四轴挂车)、C5(五轴挂车)和C6(六轴挂车)，其余车型按等效轴质量原理转换为相近车型。车型服从均匀分布，车速服从正态分布，由于车质量不能采用单一的高斯分布或极值-  I型分布描述，本文采用GMM(高斯混合模型)方法建立各车型车质量的分布函数。

文献[15]研究结果表明稀疏运行状态下车间距服从Weibull分布，而密集运行状态下车距服从Gamma分布。结合宜泸高速交通量特征与文献[15]中的研究成果，将2辆车通过同一监测断面时间间隔为2 s以上的车辆划分为稀疏运行状态，否则为密集运行状态。采用上述分布类型对宜泸高速路行车间距进行拟合，2种运行状态下的车距概率分布特征值如表2所示。由Monte Carlo抽样生成的随机车流样本如图3所示。

表2  车距概率分布特征值

Table 2  Statistical probability characteristic values of vehicle space

2.3  动力响应统计分析

按照图1所示的“基于有限元的结构动力响应分析”步骤分析随机车流下南溪长江大桥的动力响应。随机车流作用下悬索桥的动力响应主要有内力、位移、速度和加速度响应等，根据式(6)所示界限跨越率公式，主要研究加劲梁的位移和速度响应。取车流通行时间为12 min，荷载子步积分时间为0.16 s。以加劲梁L/4和L/2节点为例，位移与速度时程如图4所示。

图3  随机车流统计结果与随机样本图

Fig. 3  Statistical results and random samples of random traffic flows

采用FFT方法将位移和速度时程转换为频域内的功率谱密度，如图5所示。

图4  加劲梁L/4的位移与速度时程图

Fig. 4  Relationship between displacement of L/4 girder and time history of velocity

图5  加劲梁L/4的位移与速度的功率谱密度的关系

Fig. 5  Relationship between displacement of L/4 girder and power spectral density of velocity responses

按流程图1所示“频谱分析”步骤对图5所示位移功率谱曲线进行积分可得出稀疏运行状态和密集运行状态下节点的位移和速度响应均方根，如表3所示。

表3  加劲梁位移与速度的响应均方根

Table 3  Root-mean-sequent responses of displacement and velocity of stiffening girders

按照同样的方法可求得全桥加劲梁关键节点位移与速度响应均方根，如图6所示。

由图6可知：密集运行状态下各加劲梁节点的位移与速度响应均方根均较一般状态下的大，L/4与3L/4处的位移与速度响应均方根达到最大。密集运行状态下L/4处的位移响应均方根约为稀疏运行状态下的1.43倍。

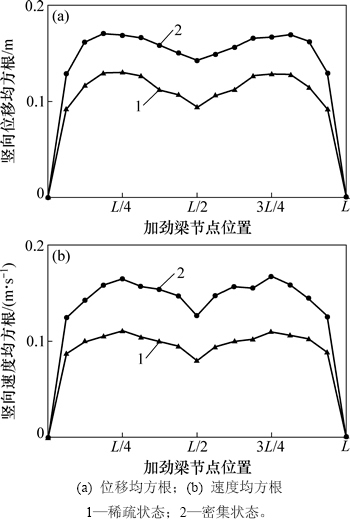
图6  全桥加劲梁节点响应均方根σ_x

Fig. 6  Root-mean-square values of displacement response of girder nodes of the bridge

3  加劲梁的位移首超动力可靠度

随机车流下悬索桥加劲梁的动力响应为随机过程。LI等^[16]的研究表明了车载下桥梁的动力响应为平稳正态随机过程，且具有广义各态历经性。因此，采用1个具有一定长度的随机车流量替代全桥的交通量是可行的。由于车辆的随机性，结构响应均方根会随运营车辆数量的变化而变化。车辆样本的长度的选取直接影响到车载下桥梁的动力响应统计值。事实上，由式(3)~(6)可知，动力可靠度的求解与时间T有关，而且结构响应均方根与界限跨越率v_b(t)有对应关系，因此，可由v_b(t)反映响应均方根随车辆样本长度的变化。

按照文献[17]，取式(6)中界限值b=L/600=1.37 m。以L/4处节点为例，40 min内节点的v_b(t)变化趋势如图7所示。

图7  加劲梁L/4界限跨越率随时间变化趋势 (稀疏和密集状态下v_b(t)的单位分别为10^-21和10^-15)

Fig. 7  Boundary crossing rate of displacement of node in l/4 of stiffening girders

由图7可知：随着时间的延长，跨越率趋于稳定，其中稀疏运行状态下的位移界限跨越率约3.48×10^-21，密集运行状态下的位移界限跨越率约4.30× 10^-15。事实上，随着车辆样本数量的增加，桥梁结构的动力响应均方根趋于稳定，因此，界限跨越率也趋于稳定。

根据监测系统的车辆数量可知，密集运行状态车辆占单日车辆总数的比例a=1.29%。为了能够反映真实交通量，取实际运行状态车辆中密集状态车辆占有率为1.29%，稀疏运行状态车辆占有率为98.71%。由式(8)可得出100 a内加劲梁1/4跨节点位移动力可靠指标随时间变化趋势如图8所示。

由图8可知：随着运营时间增加，悬索桥动力可靠指标下降趋势较缓；在100 a内，稀疏运行状态下悬索桥动力可靠指标由7.30降至6.65；密集运行状态下的动力可靠指标由5.16降至4.22；实际运行状态下的动力可靠指标由5.92降至5.11，介于稀疏运行状态与密集运行状态值之间。

图8  不同运行状态下可靠指标随时间的变化

Fig. 8  Influence of service time on reliability index under different operational states

实际交通量随时间逐步增大，动力响应的均方根随之增大，因此，交通量对动力可靠指标产生一定影响。密集状态车辆所占比例增加后，当日的总交通量也会随之增大，因此，可采用密集状态车辆所占当日总交通量的比例来模拟交通量增大量。在100 a内，密集状态车辆不同占有率下的可靠指标的变化如图9所示。

由图9可知：密集车辆的占有率对可靠指标有较大影响；在第1年运营期内，当密集运营车辆占有率从0增至0.1%时，1/4跨加劲梁位移动力可靠指标由7.30下降至6.33；当密集运营车辆占有率从0.1%增至4.0%时，1/4跨加劲梁节点位移动力可靠指标仅由6.33下降至5.74。

图9  密集车辆占有率对可靠指标的影响

Fig. 9  Influence of heavy vehicle proportion on reliability index

南溪长江大桥的实际密集车辆占有率a=1.28%，实际密集车辆占有率对加劲梁位移首超动力可靠指标的影响如图10所示。

由此可知：在不考虑桥梁结构抗力退化的情况下，随机车流作用下悬索桥加劲梁位移超限失效事件主要是存在密集运行车辆荷载所致，且随着密集运行车辆的增大，其可靠指标下降趋势减缓。密集运行车辆的存在是导致悬索桥位移动力可靠度降低的重要因素。

图3  实际密集车辆占有率a与运营时间对动力可靠指标的影响

Fig. 10  Influence of heavy traffic proportion and service time on dynamic reliability index

4  结论

1) 建立了基于位移首超准则的随机车流下桥梁动力可靠度数学模型，给出了考虑多个交通量参数的桥梁动力可靠度分析方法。

2) 随机车流下悬索桥加劲梁L/4的位移均方根最大，车辆密集状态下的位移均方根约为稀疏状态下的1.43倍，界限跨越率随着随机车流样本数量的增加趋于平稳。

3) 随着运营时间增长，实际运行状态下悬索桥加劲梁位移动力可靠度呈减速下降趋势，其数值介于稀疏运行状态与密集运行状态之间。

4) 悬索桥加劲梁位移超限失效事件主要由密集车辆引起，可靠指标随密集车辆占有率的增大而下降，随时间的延长可靠指标下降趋势渐缓。密集运行车辆的存在是导致悬索桥位移动力可靠度降低的重要因素。

5) 在车载下悬索桥的动力响应方面，将车辆简化为单自由度模型；在随机变量方面，仅考虑车辆的随机性，忽略了桥梁参数的随机性。这都需进一步研究。

参考文献：

[1] 王达, 刘扬, 黄平明. 随机车流作用下双曲拱桥车-桥耦合振动研究[J]. 中国公路学报, 2009, 22(6): 67-73.

WANG Da, LIU Yang, HUANG Pingming. Research on vehicle-bridge coupled vibration for two-way curved arch bridge under random traffic flow[J]. China Journal of Highway and Transport, 2009, 22(6): 67-73.

[2] 韩万水, 陈艾荣. 随机车流下的风-汽车-桥梁系统空间耦合振动研究[J]. 土木工程学报, 2008, 41(9): 97-102.

HAN Wanshui, CHEN Airong. Three-dimensional coupling vibration of wind-vehicle-bridge systems under random traffic flow[J]. China Civil Engineering Journal, 2008, 41(9): 97-102.

[3] 邓子铭, 郭向荣, 张志勇. 地震作用对钢桁梁桥车桥系统耦合振动的影响分析[J]. 中南大学学报(自然科学版), 2011, 42(1): 184-191.

DENG Ziming, GUO Xiangrong, ZHANG Zhiyong. Coupled vibration of train-bridge system of steel truss bridge with seismic effect[J]. Journal of Central South University (Science and Technology), 2011, 42(1): 184-191.

[4] XIANG Tianyu, ZHAO Renda, XU Tengfei. Reliability evaluation of vehicle-bridge dynamic interaction[J]. Journal of Structural Engineering, 2007, 133(8): 1092-1099.

[5] 刘扬, 鲁乃唯, 殷新锋. 基于体系可靠度的钢桁梁结构优化设计[J]. 中南大学学报(自然科学版), 2014, 45(10): 3629-3636.

LIU Yang, LU Naiwei, YIN Xinfeng. Structural optimization design of steel truss beam based on system reliability[J]. Journal of Central South University (Science and Technology), 2014, 45(10): 3629-3636.

[6] 周剑波. 基于随机车流的桥梁动力特性与可靠性研究[D]. 西安: 长安大学公路学院, 2009: 49-64.

ZHOU Jianbo. The dynamic characteristics and reliability of bridge based on random traffic flows[D]. Xi’an: Changan University. Highway Institute, 2009: 49-64.

[7] 夏禾, 张楠. 车辆与结构动力相互作用[M]. 北京: 科学出版社, 2005: 75-90.

XIA He, ZHANG Nan. Dynamic interaction of vehicles and structures[M]. Beijing: Science Press, 2005: 75-90.

[8] 施颖, 宋一凡, 王荣波. 基于有限元的曲线连续梁桥车桥耦合振动分析[J]. 公路交通科技, 2010, 27(4): 95-100.

SI Ying, SONG Yifan, WANG Rongbo. Analysis on coupled vibration of vehicle and curved continuous beam bridge based on FEM[J]. Journal of Highway and Transportation Research and Development, 2010, 27(4): 95-100.

[9] 陈颖, 王东升, 朱长春. 随机结构在随机荷载下的动力可靠度分析[J]. 工程力学, 2006, 23(10): 82-85.

CHEN Yin, WANG Dongsheng, ZHU Changcun. Dynamic reliability analysis of stochastic structures subjected to random loads[J]. Engineering Mechanics, 2006, 23(10): 82-85.

[10] 刘佩, 姚谦峰. 随机结构动力可靠度估计算法的对比分析[J]. 地震工程与工程振动, 2009, 29(6): 48-52.

LIU Pei, YAO Qianfeng. Approximate methods for dynamic reliability calculation of stochastic structures[J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(6): 48-52.

[11] RICE S O. Mathematical analysis of random noise[J]. Bell System Technical Journal, 1945, 24(1): 146-156.

[12] LI J, MOSLEH A, KANG R. Likelihood ratio gradient estimation for dynamic reliability applications[J]. Reliability Engineering & System Safety, 2011, 96(12): 1667-1679.

[13] 李枝军, 李爱群, 韩晓林. 润扬大桥悬索桥动力特性分析与实测变异性研究[J]. 土木工程学报, 2010, 43(4): 92-98.

LI Zhijun, LI Aiqun, HAN Xiaolin. Dynamic analysis and experimental study of variations of the dynamic parameters of the Runyang suspension bridge[J]. China Civil Engineering Journal, 2010, 43(4): 92-98.

[14] 王达. 基于有限元模型修正的大跨度悬索桥随机车流车-桥耦合振动分析[D]. 西安: 长安大学公路学院, 2008: 100-137.

WANG Da. Analysis of vehicle-bridge coupled vibration for long-span suspension bridge with finite element model updating under random traffic flowing[D]. Xi’an: Chang’an University. Highway Institute, 2008: 100-137.

[15] 宗周红, 李峰峰, 夏叶飞, 等. 基于 WIM 的新沂河大桥车辆荷载模型研究[J]. 桥梁建设, 2013, 43(5): 29-36.

ZHONG Zhouhong, LI Fengfeng, XIA Yefei, et al. Study of vehicle load models for Xinyi river bridge based on WIM data[J]. Bridge Construction, 2013, 43(5): 29-36.

[16] LI Yongle, QIANG Shizhong, LIAO Haili, et al. Dynamics of wind–rail vehicle–bridge systems[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(6): 483-507.

[17] JTG/T H21—2011, 公路桥梁技术状态评定标准[S].

JTG/T H21—2011, Standards for technical condition evaluation of highway bridge[S].

(编辑  陈灿华)

收稿日期：2015-11-07；修回日期：2016-01-09

基金项目(Foundation item)：国家重点基础研究发展计划(973计划)项目(2015CB057700)；国家自然科学基金资助项目(51378071)；桥梁结构安全控制湖南省工程实验室(长沙理工大学)开放基金资助项目(14KD05)(Project(2015CB057705) supported by the National Basic Research Program (973 Program) of China; Project(51378071) supported by the National Natural Science Foundation of China; Project(14DK05) supported by Engineering Laboratory of Bridge Structure (Changsha University of Science & Technology) of Hunan Province)

通信作者：鲁乃唯，博士(后)，从事桥梁结构可靠度评估与安全控制研究；E-mail：lunaiweide@163.com