简介概要

纳秒脉冲激光辐照金属玻璃表面结构形成机制

来源期刊：稀有金属2017年第10期

论文作者：叶林茂熊向明刘凯欣孙贵磊

文章页码：1061 - 1068

关键词：激光辐照;金属玻璃;表面波;波群;等离子体相互作用;

摘要：脉冲纳秒激光辐照金属玻璃材料会在表面产生一种特殊的波纹形貌,波纹的波长和振幅由内至外逐渐减小。利用扫描电镜（SEM）和原子力显微镜（AFM）观测了一种Ti基金属玻璃Ti₄₀Zr₂₅Cu₁₂Ni₃Be₂₀（%,质量分数）被纳秒脉冲激光辐照后表面的波纹形貌。与Zr基和La金属玻璃的实验结果相比,Ti基金属玻璃表面波纹形貌具有更广的范围和更小的特征尺度。在实验观测基础上进行合理的假设来简化模型,假设波纹形貌是由于小振幅表面波在深水域不可压粘性液体中传播,并在传播过程中被凝固而形成的。考虑波群理论和等离子体与熔融液体相互作用的影响,对实验结果进行理论分析。理论分析表明波长短的波传播更快,凝固前波传播的距离更远,所以越靠近边缘波的波长越短,分析结果也可以解释Ti基金属玻璃表面波纹范围更广的原因。此外,激光辐照金属玻璃会电离产生等离子体,通过理论计算发现变化的等离子体速度、密度和粘性等条件也会影响波纹形貌的形成,不同等离子体条件对应不同的波数,亦可通过实验数据观测的波数值反推等离子体条件。

网络首发时间: 2016-10-26 08:40

稀有金属 2017,41(10),1061-1068 DOI:10.13373/j.cnki.cjrm.xy16060025

纳秒脉冲激光辐照金属玻璃表面结构形成机制

叶林茂熊向明刘凯欣孙贵磊

北京大学工学院湍流与复杂系统国家重点实验室

中国劳动关系学院安全工程系

摘要：

脉冲纳秒激光辐照金属玻璃材料会在表面产生一种特殊的波纹形貌, 波纹的波长和振幅由内至外逐渐减小。利用扫描电镜 (SEM) 和原子力显微镜 (AFM) 观测了一种Ti基金属玻璃Ti₄₀Zr₂₅Cu₁₂Ni₃Be₂₀ (%, 质量分数) 被纳秒脉冲激光辐照后表面的波纹形貌。与Zr基和La金属玻璃的实验结果相比, Ti基金属玻璃表面波纹形貌具有更广的范围和更小的特征尺度。在实验观测基础上进行合理的假设来简化模型, 假设波纹形貌是由于小振幅表面波在深水域不可压粘性液体中传播, 并在传播过程中被凝固而形成的。考虑波群理论和等离子体与熔融液体相互作用的影响, 对实验结果进行理论分析。理论分析表明波长短的波传播更快, 凝固前波传播的距离更远, 所以越靠近边缘波的波长越短, 分析结果也可以解释Ti基金属玻璃表面波纹范围更广的原因。此外, 激光辐照金属玻璃会电离产生等离子体, 通过理论计算发现变化的等离子体速度、密度和粘性等条件也会影响波纹形貌的形成, 不同等离子体条件对应不同的波数, 亦可通过实验数据观测的波数值反推等离子体条件。

关键词：

激光辐照;金属玻璃;表面波;波群;等离子体相互作用;

中图分类号： TG139.8;TG665

作者简介：叶林茂 (1985-) , 男, 黑龙江人, 博士研究生, 研究方向:冲击动力学、金属玻璃、形状记忆合金, E-mail:LmLeaf@pku.edu.cn;;孙贵磊, 副教授, 电话:010-88562059, E-mail:lmleaf@pku.edu.cn;

收稿日期：2016-06-20

基金：国家自然科学基金项目 (10732010, 10972110, 11028206) 资助;

Mechanism for Formation of Rippling Structure on Surface of Metallic Glasses Irradiated by Pulse Nanosecond Laser

Ye Linmao Xiong Xiangming Liu Kaixin Sun Guilei

State Key Laboratory for Turbulence & Complex Systems, College of Engineering, Peking University

Department of Safety Engineering, China Institute of Industrial Relations

Abstract：

Special concentric rippling wave were produced on the metallic glasses surface after pulse nanosecond laser irradiation.The wavelength and amplitude decreased from the inside to the outside part. The surface of metallic glass Ti₄₀Zr₂₅Cu₁₂Ni₃Be₂₀ ( %, atom fraction) irradiated by laser was observed by scanning electron microscope ( SEM) and atomic force microscope ( AFM) . There was vaster range and shorter wavelength and amplitude, compared to Zr-based and La-based metallic glasses. The formation of ripples was assumed as that small amplitude surface wave was solidified when propagating in deep incompressible viscous fluid. Wave group and the interaction between plasma and molten liquid were considered for the theory and experimental analysis. It was concluded that the shorter the wavelength was, the faster and farther the wave spread based on wave group theory. So, the wavelength was shorter near the edge and Ti-based metallic glasses had vaster rippling range. It was also concluded that the conditions of plasma of metallic glasses above the surface such as the velocity, density and viscosity affected the formation of ripples. The wavenumbers were different under various plasma conditions, which could be inferred from the experimental observation of wavenumbers.

Keyword：

laser irradiation; metallic glasses; surface waves; wave group; plasma interactions;

Received： 2016-06-20

金属玻璃微观结构具有长程无序、短程有序的特点, 因此表现出许多优良特性^[1,2,3,4,5], 并被应用于多个领域^[6]。激光由于其短周期高能量等特性而常被用在材料微纳米尺寸加工上^[7,8,9,10]。激光辐照金属玻璃可以对其微晶化和改良磁性能等^[11,12]。激光辐照金属玻璃表面微观结构形成的机制分析也是一个研究热点^{[13,14,15,16,17,18,19]}。激光辐照金属玻璃, 可以在表面形成一种特殊的同心圆波纹结构。研究这种表面结构将有助于材料的定量微纳米尺度加工及进一步认识材料特性。这种结构与表面波传播类似, 等离子体也可能是其产生的原因^[20]。文献[13-14]分别单独从波群的传播和粘性变化的角度研究了激光辐照Zr和La基金属玻璃表面波纹形貌形成的原因。Liu等^[16]通过考虑熔融金属与上方等离子体相对剪切运动, 以及引发的K-H不稳定性 (Kelvin-Helmholtz instability) 来计算典型波数。但研究多集中分析单一因素或忽略某些物理量的变化, 如粘性和等离子速度等。本文研究了群速度和粘性共同作用对波纹形貌形成的影响, 并分析了变化的等离子速度对最优波数的影响。

1实验

采用电弧熔炼-铜模吸铸的方法制备了一种Ti金属玻璃。选取纯度在99.99%以上的Ti, Zr, Cu, Ni和Be纯金属按分子式Ti₄₀Zr₂₅Cu₁₂Ni₃Be₂₀ (%, 原子分数) 配比材料, 熔炼制备25 g金属玻璃母合金锭, 然后采用铜模吸铸的方法制备直径为5 mm的棒状金属玻璃Ti₄₀Zr₂₅Cu₁₂Ni₃Be₂₀ (%, 原子分数) , 并切割成高5 mm的圆柱状。对试件进行抛光处理, 使得表面粗糙度小于50 nm。采用QuantaRay Pro-350固体激光器 (spectra-physics) 发出的Nd:YAG脉冲激光对抛光后的材料表面进行照射, 实验环境为氩气环境。激光选取qs模式, 脉宽10ns, 波长532 nm, 能量密度约为5.5×10¹²W·m^-2。在激光辐照实验前和实验后分别对金属玻璃表面进行X射线衍射 (XRD) 实验。采用扫描电镜 (SEM, S-4800) 在低倍和高倍观测激光辐照金属玻璃表面波纹的整体和局部的二维形貌。采用原子力显微镜 (AFM, ICON) 观测表面波纹的三维形貌, 从波纹的内侧向外侧逐步扫描, 获得整个波纹形貌的波长和振幅等特征尺度数据。

2结果与讨论

2.1结果

激光辐照Ti基金属玻璃Ti₄₀Zr₂₅Cu₁₂Ni₃Be₂₀ (%, 原子分数) 的实验结果如图1所示。图1给出了SEM和AFM对表面波纹形貌的观测图。图1 (a) 是辐照后金属玻璃表面的整体二维形貌, 放大倍数为300倍, 从图1 (a) 中可以观测到中间区域凹陷, 有熔化重新凝固的痕迹, 边缘处有同心圆波纹形貌, 其范围相对整个激光辐照区域小。图1 (b) 给出了对应图1 (a) 中A区域的高倍观测图, 放大倍数为1300倍, 从图中可以看到边缘处同心圆形貌的变化情况, 波纹的波长和振幅由内至外逐渐减小。图1 (c) 和 (d) 分别对应图1 (b) 中标记的B和C区域, 放大倍数为10000倍。波纹内侧B区域处的波长和振幅明显小于外侧C区域处的。图1 (e) 和 (f) 给出了原子力显微镜观测的波纹中部区域形貌。图1 (e) 为二维形貌图, 图1 (f) 为对应的三维观测图。通过实验观测发现纳秒脉冲激光辐照金属玻璃Ti₄₀Zr₂₅Cu₁₂Ni₃Be₂₀后, 形成同心圆波纹的波长变化范围约从2.0~0.5μm, 振幅约从200~80 nm。

图1 纳秒脉冲激光辐照金属玻璃Ti40Zr25Cu12Ni3Be20表面波纹形貌二维观测图和中部区域的三维观测图Fig.1 Two-dimensional observations of ripples and three-dimensional observations for middle part of surface of metallic glass Ti40Zr25Cu12Ni3Be20irradiated by pulse nanosecond laser (a) Observation for whole ripples by SEM; (b) Observation for area“A”signed in (a) under higher magnification (1300times) ; (c) Observation for area“B”signed in (b) under higher magnification (10000 times) ; (d) Observation for area“C”signed in (b) under higher magnification (10000 times) ; (e) Three-dimensional observation for middle area of ripples by AFM

2.2基本模型

激光与金属玻璃的相互作用经历了复杂的物理和化学变化。激光辐照金属玻璃造成材料表面熔化, 辐照区域的温度与激光能量密度分布有关, 符合高斯分布, 辐照区域中心处比边缘处的温度高, 中心处温度足够高甚至发生气化和电离。随着辐照时间的增加, 材料表面的电离程度逐渐增大, 产生的等离子体数量逐渐增加。激光辐照结束后, 等离子体的密度和能量增加到极大并迅速膨胀, 产生冲击力作用于辐照材料表面的中心区域, 形成扰动并以波或波群的形式在表面熔化区域由内向外传播。等离子体在周向膨胀过程中也会和熔融的材料相互作用。激光辐照结束后, 材料迅速凝固, 表面的波纹形貌也迅速地被凝固, 进而形成了观测到的特殊波纹形貌。

本文主要关注材料表面波纹形貌形成的力学机制, 在实验基础上通过一定的合理假设来简化模型。假设气化和等离子体冲击造成金属玻璃熔化区域的中心处凹陷, 与图1实验观测的结果相符;熔化区边缘处的波纹形貌主要是由于表面波或波群的传播而形成;表面波为小振幅波, 液域为深水域, 在传播过程中波或波群未传到固体边界处, 即没有反射;在激光加热过程中, 金属玻璃的密度随温度变化不明显, 近似认为液体不可压;假设表面波在每个周期内物理参数, 如粘性等为恒定, 但在整个波纹区间, 粘性随着位置变化较为明显, 影响波的形貌^[14]。综上, 波纹形貌的形成被假设为:激光辐照引起材料熔化和电离, 等离子体膨胀冲击作用于熔化区域引起扰动, 并以小振幅表面波的形式由内向外、在半无限液体域中传播, 波在传播过程中液体被凝固, 进而形成了金属玻璃表面特殊波纹形貌, 基本模型示意图如图2所示。

通过对观测的实验结果进行分析, 可以验证基本模型中的假设具有合理性。波纹形貌的波长比振幅大近一个量级, 所以波为小振幅表面波。激光熔化区域深度在数十微米量级以上^[14], 远大于波长百纳米量级, 所以表面波是在深液域中传播的。如图1 (a) 和 (b) 所示, 波纹外边缘处, 材料有熔化的迹象但没有波纹产生, 同时波纹边缘处没有明显波叠加的现象, 波长单调递减, 表明波没有传播到边界, 即没有反射。由实验结果观测到, 表面有近百个周期, 平均每个周期特征长度 (波长和振幅) 变化仅为1%左右, 所以在单个周期内各参数近似恒定。

图2 激光辐照金属玻璃表面波纹形貌形成机制示意图Fig.2 Sketch for formation mechanism of ripples on metallic glasses'surface after laser irradiation

基于假设, 建立控制方程并进行求解。选取欧拉坐标系, 原点定为波纹起始位置, x轴为沿波纹传播方向, y轴沿波纹的周向, z轴沿试件轴向向下。在初始时刻, z=0为自由面。因为激光光斑的形状为轴对称圆形, 并且图1实验结果观测到波纹区域也为近似圆形, 所以可以将波纹形貌近似看作轴对称, 将三维问题简化为二维问题, 质点的速度可以表示为 (u, w) 。外力项、非线性项和重力项与线性项和表面张力项相比可以忽略, 恢复力主要表现为表面张力^[14]。在单个周期内的表面波建立控制方程式 (1) 和自由面 (z=0) 界面条件式 (2) 。

式中, ρ为材料密度 (kg·m^-3) , x轴沿波纹径向从内向外 (波纹传播方向) , z轴沿波纹垂向向下, u为质点沿x轴方向的速度 (m·s^-1) , w为质点沿z轴方向的速度 (m·s^-1) , t为时间变量 (s) , P为流体的压力 (Pa) , μ为流体的动力粘性系数 (Pa·s) , g为重力加速度 (m·s^-2)。

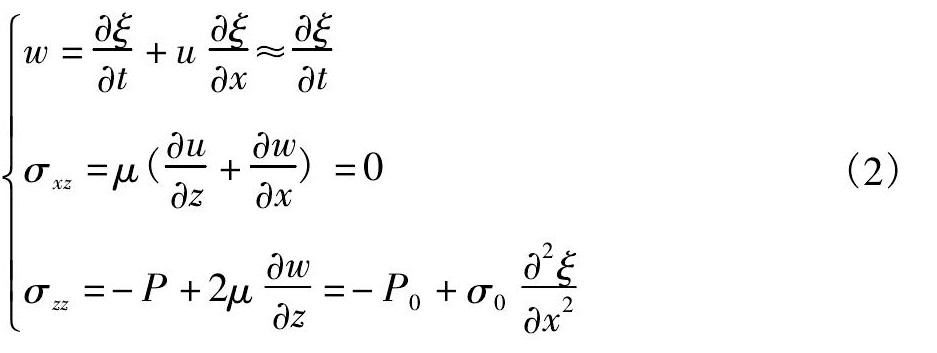
式中σ_xz为流体的切向应力 (Pa) , σ_zz为流体的法向应力 (Pa) , σ₀为表面张力系数 (N·m^-1) 。y=ξ (x, t) 为扰动后的液气交界面函数 (m) 。P₀为液面z=0处的压强, 在单个周期内不随变化。当界面是水平时, z<0的部分为液体。

2.3波群对波纹形成的影响

前期工作^[14]对控制方程求解得到式 (3) , 在粘性较大时, 近似忽略|ρω/k²μ|项, 得到控制方程的解。

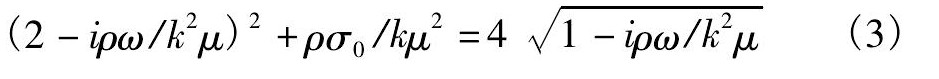
式中i为虚数, k为波数 (m^-1) , ω为简振模式的复频率。

本文在此基础上引入波群理论进一步精确求解, 保留|ρω/k²μ|项, 波数k=2π/λ为实数, λ为波长 (m) , 对式 (3) 进行进一步精确求解。

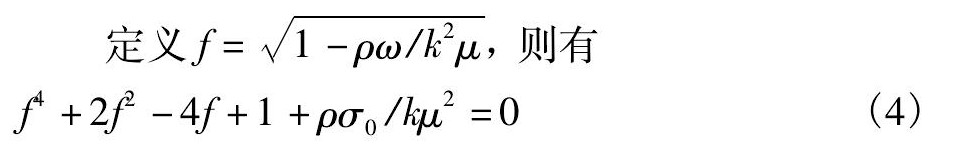
金属玻璃Ti₄₀Zrc₂₅Cu₁₂Ni₃Be₂₀ (%) 的密度ρ为5380 kg·m^-3, 表面张力系数σ₀约为1 N·m^-1, 粘性系数μ>1 Pa·s, 由实验观测知波数k>10⁶m^-1, 则近似ρσ₀/kμ²< (5380×1) / (10⁶×1²) <<1, 公式 (4) 可以写作

解方程 (5) 得到四个根

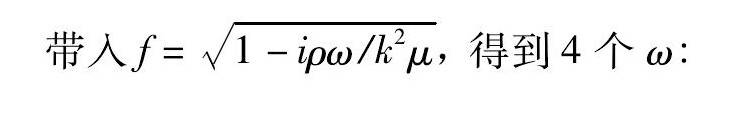
考虑ρσ₀/kμ²的一阶修正, 设f_j的根被修正为f_j (1+ε_j) , ε_j为修正小量, 即:

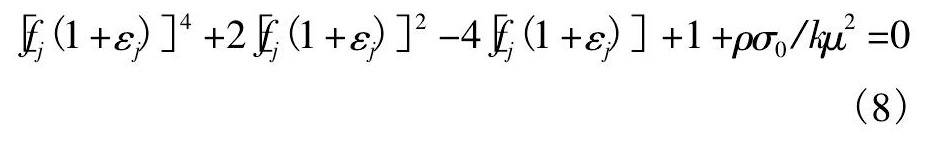
近似有

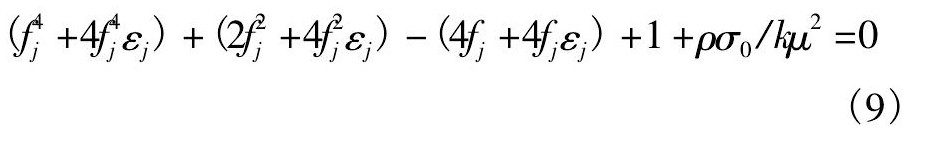
从公式 (9) 中减去f_j满足的方程f_j⁴+2f_j²-4f_j+1=0, 得到

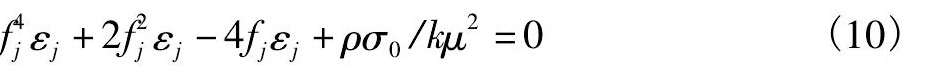
即

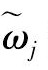
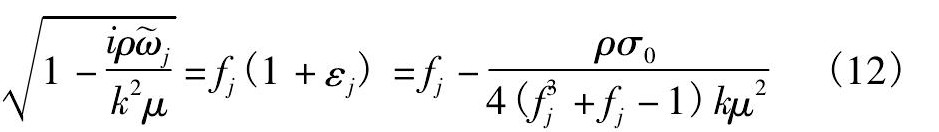
修正后满足

即

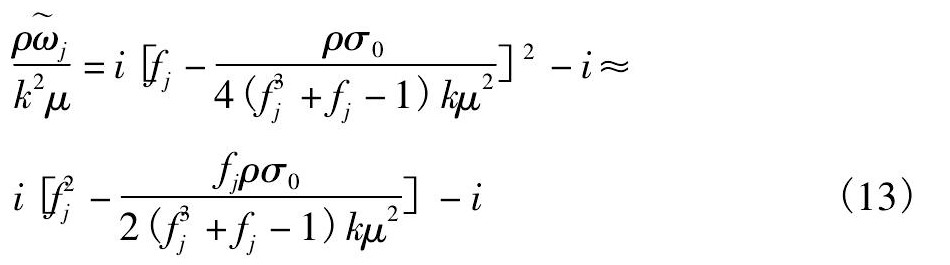
得到4个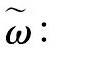

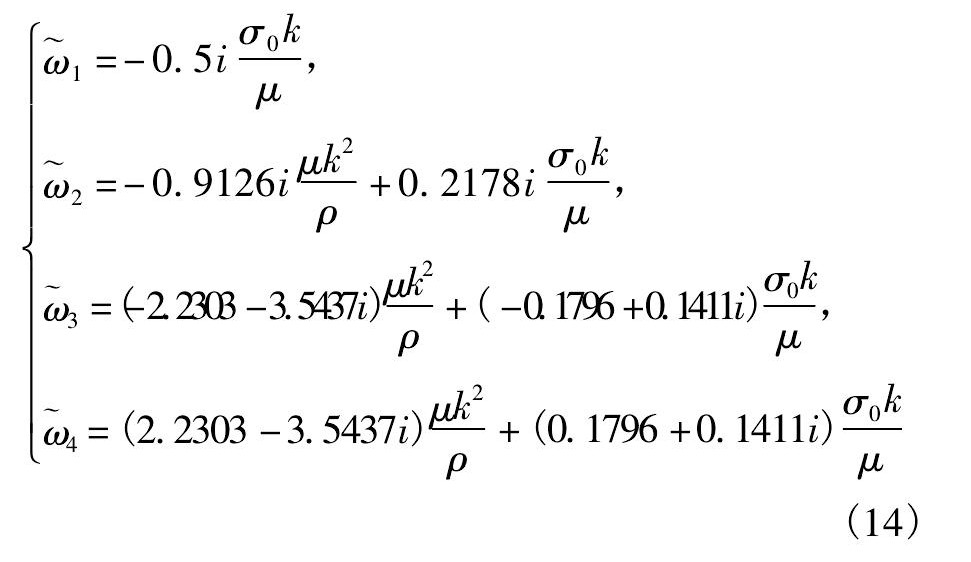
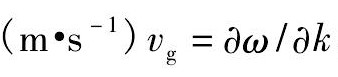
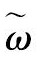
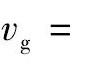
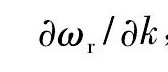
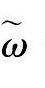
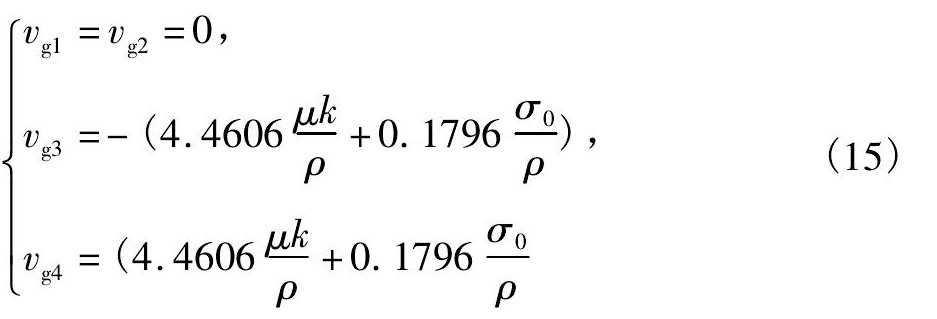
考虑群速度 , 因为ω_i (s^-1) 表示扰动随时间的增长率 (因为4个都有负虚部, 实际上扰动随时间衰减) , 则群速度为 , 将公式 (14) 的4个带入群速度公式得到

从上面的结果可以看到, 第一种和第二种模态的群速度为0 m·s^-1, 所以对应的是驻波, 不会传播到别的地方;第三种模态的群速度为负值, 是反射波, 对应的波从外向内传播。根据实验观测到波纹边缘外的区域有熔化痕迹但无波纹形貌的现象, 可以假设波没有反射, 所以前3种模态不符合实验结果。边缘的扰动对应第四种模态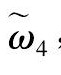 , 群速度为正值。从ν_g4的公式可以看到波长较短的波 (k较大的波) 传播速度较快, 在材料凝固前波长较短的波传播的距离较远, 所以越靠近外侧边缘的地方波的波长越短。因为粘性高的金属玻璃材料具有更小的波长和振幅, 所以其波的传播距离更远, 也具有更为广阔的波纹范围。

在粘性恒定的情况下, 考虑波群对波纹和振幅定量影响。首先假设熔融态的金属玻璃的各点都是在τ₀时刻同时凝固的 (沿着z轴方向凝固) , 设激光引起的初始扰动在x₀处开始以表面波形式向外传播, 初始振幅为A₀, 则τ₀时刻在x处表面波的传播速度 (群速度) 为

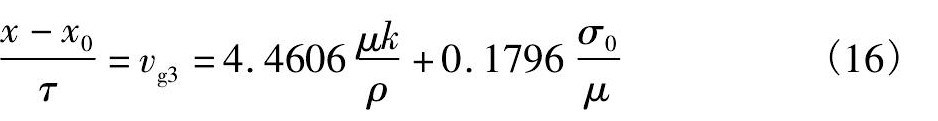
式中τ为时间变量 (s) 。

波数 (m^-1) 为

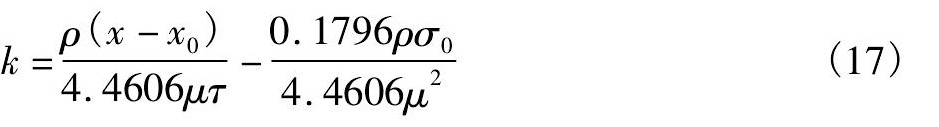
波长 (m) 为

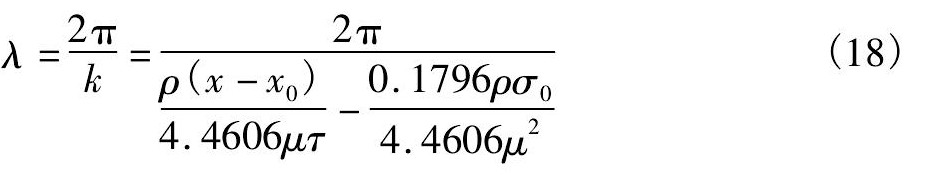
振幅 (m) 为

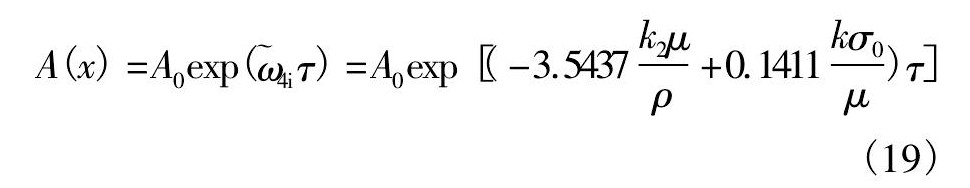
在粘性较小时, |ρω/k²μ|>>1, 则公式 (3) 近似为 (-iρω/k²μ) ²+ρσ₀/kμ²=0, 可以得到ω²=k³σ₀/ρ, 退化得到前期工作^[13]介绍的情形。

通过上面的分析知道当粘度恒定不随温度变化时, 随着x的增加, 波数k越大, 波长λ越小, 振幅A越小。粘性、波长和速度随x的变化有两种尺度, 小尺度上每个波从波峰到波谷, 速度有急剧震荡。而在大尺度上, 表现为宏观上不同位置处的粘性, 波长, 速度幅值变化相对缓慢。每个波长内的物理量远小于小尺度上的变化。所以可以在空间上局部求解, 即把空间划分为一系列小区域, 每个小区域包含一定波长, 即微观足够大宏观足够小。假设每个小区域内粘性系数为常数, 可以得到局部解析解。但整个范围内粘性系数的变化不可忽略。不同小区域的粘性系数不同, 拼接每个小区域的解, 可以得到粘性的宏观变化。表面波按照所处区域的波群速度行进, 不同传播速度即波到终点时的波数对应的速度, 衰减消耗为传播到相应终点经历的整个路程内的消耗, 振幅衰减只与总的传播时间有关。粘性在整个范围的变化不可忽略, 可以在局部解中引入粘性的变化, 通过实验数据的波长和振幅情况反推粘性随着位置变化的情况。

前期分别从波群的传播和粘性变化对波纹形貌形成的影响两个角度出发, 研究了金属玻璃表面不同位置处波纹的波长和振幅变化的原因^[13,14]。本节在其基础上, 同时考虑群速度和粘性, 分析了粘性系数对波的群速度的影响, 是前期研究结果的推广, 不仅适用于粘性较大的情况, 甚至粘性系数不是常数的情形也适用。前期的结果^[13]仅是本文结论的一种特例, 即粘性系数趋于零时的情形。

2.4表面上等离子体对波纹形成的影响

当等离子体扩散时, 会作用于熔融的金属玻璃材料表面, 此时合金表面会由于界面不稳定而产生波纹, 这种现象类似风吹过水面产生的涟漪。Zeisei和Valenzuela等^[21,22]对风吹过水面的现象进行了充分的研究, 本文参考这种现象, 类似地假设等离子体的速度剖面为分段函数“lin-log”剖面, 表示为^[21]

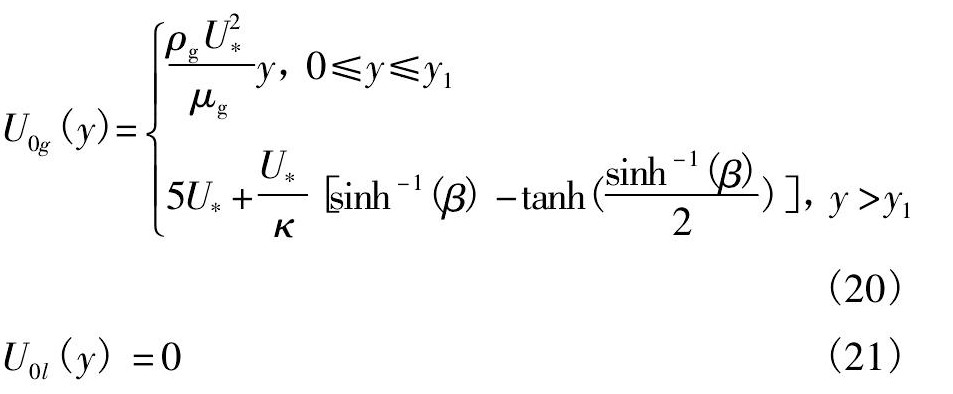
本节在Zeisel等^[21]研究水气界面不稳定性方法的基础上, 扩展到更大的控制参数范围, 使其可以模拟等离子体风吹过熔融金属合金表面时所形成的表面波纹。依照Zeisel的方法, 可以推导得到一个常微分方程的特征值问题, 特征值ω表示简振模态的复频率, 其虚部ω_i表示时间增长率 (s^-1) 。在给定的密度和粘性系数等控制参数下, 采用Chebyshev配点法求解这个特征值问题, 得到不同控制参数下, 时间增长率ω_i对扰动波数k的依赖关系, 找到有增长潜力的扰动波数范围。若时间增长率在某个k上取得最大值, 则这个k应当是实验中观测到的波数。选取两组不同表面气体参数, 计算结果如下所示。

(1) 考虑熔化的液体表面上方为空气的情况。重力加速度g=9.81 m·s^-2, 熔融金属玻璃密度 (本文实验采用金属玻璃Ti₄₀Zr₂₅Cu₁₂Ni₃Be₂₀) ρ_l=5380 kg·m^-3, 表面张力系数α=1 N·m^-1, 假设摩擦速度为U_*=1000 m·s^-1, 等离子体密度ρ_g=1kg·m^-3, 等离子体粘性μ_g=1×10^-4Pa·s, 熔融金属玻璃的粘性μ_l=100 Pa·s, 计算得到时间增长率随波数变化的曲线μ_i (k) , 如图3所示。

计算结果显示, 时间增长率作为波数的函数是单调下降的, 即当k=0时有最大的时间增长率。这与实验结果不符合。

(2) 考虑熔化的液体表面为等离子体, 即表面气体的密度和粘度较大的情况, 根据已有文献^[23]适当选取等离子体摩擦速度的参数。当g=9.81m·s^-2, ρ_l=5380 kg·m^-3, 表面张力系数α=1N·m^-1, 并近似假设摩擦速度为U_*=2×10⁵m·s^-1, 等离子体密度ρ_g=10 kg·m^-3, 等离子体粘性μ_g=0.01 Pa·s, 熔融金属玻璃的粘性μ_l=100 Pa·s时, 计算得到时间增长率随波数变化的曲线w_i (k) 如图4所示。

图3 熔化液体表面上方为空气时对应的时间增长率随波数变化曲线Fig.3 Curve for temporal growth rate with various wave num-bers under condition that gas above molten liquid sur-face being air

计算结果显示, 时间增长率作为波数的函数, 在k=3.5×10⁶m^-1时, 时间增长率取得最大值为1.15×10¹¹s^-1, 最优波数与实验结果吻合。

本节从等离子体影响的角度, 理论上解释了实验中观测到的典型波数, 与Liu等^[16]类似都考虑了熔融金属与它上方的等离子体的相对剪切运动, 并从这种相对剪切运动引发的流体力学K-H不稳定性出发来计算最优波数。但本文采用的计算方法参考Zeisei等^[21]关于风吹过水面的研究结果。与Liu在每个算例里假设等离子体速度是常数不随空间变化不同, 本文假设等离子体的速度随空间位置变化剖面为“lin-log”剖面 (式 (20) , (21) ) , 这种假设更符合真实的物理情况。同时, 熔融金属的速度远小于等离子体的速度, 对计算结果影响很小, 因此可假设熔融金属的速度为零。此外, 在本文中, 理论上的最优波数被定义为对应于最大时间增长率的波数, 即增长最迅速的波数 (图4) ;比Liu定义最优波数为临界波数 (增长率为零的波数) 的倍^[16], 具有更明确的物理意义。可见, 本节的结果更加直观, 且充分考虑到了等离子体运动速度随空间位置的变化, 更接近真实的物理情形。

图4 熔化液体表面上方为等离子体时所对应的时间增长率随波数变化曲线Fig.4 Curve for temporal growth rate with various wave num-bers under condition that gas above molten liquid sur-face being plasma

通过上面分析发现等离子体的条件, 如速度、密度和粘度等对最优特征波数的取值有影响, 等离子体与熔融液体的相互作用也是影响金属玻璃表面波纹形貌的因素。通过不同位置实验观测到的波数及液体粘性的数据可以反推不同位置等离子体的参数。

实验结果显示, 在近似相同的实验条件下, 与Zr基金属玻璃和La基金属玻璃^[13,14]相比, Ti基金属玻璃表面波纹的波长和振幅等特征尺度更小, 覆盖的范围更广, 这与Ti基金属玻璃具有更高粘性相关。上述波群理论推导结果显示粘性高的金属玻璃材料具有更小的波长和振幅, 其波的传播距离更远, 具有更为广阔的波纹范围, 实验结果很好的验证了这一结论。实验观测得到的波数量级和图4中拟合得到的最优波数相符, 验证了等离子体的速度、密度和粘度等条件对波纹的形成具有影响。

3结论

1.实验观测了脉冲纳秒激光辐照金属玻璃, 在材料表面会形成同心圆波纹形貌, 波长和振幅由内向外逐渐减小。这种波纹形貌形成的基本模型可以假设为激光辐照电离部分金属玻璃材料, 辐照结束后产生的等离子体膨胀冲击作用于熔融的材料液体, 引起扰动, 扰动以小振幅表面波的形式在半无限液体域中传播, 传播过程中材料被凝固, 由此形成了金属玻璃的表面波纹形貌。实验观测发现波纹形貌的波长比振幅大近一个量级, 验证了波是小振幅表面波。激光熔化区域的深度远大于波长, 证明表面波在深液域中传播的。波纹外边缘处有熔化迹象但没有波纹的产生, 波纹边缘处没有明显波叠加的现象, 表明波在凝固前没有反射。

2.通过波群理论的分析, 波纹的波长和振幅单调递减可能是由于波群中波的波速不同造成的。因为波群中波长短的波传播速度快, 在材料凝固前其传播距离远, 所以越靠近边缘的地方波的波长越短。此外, 引入波群的理论还可以解释纳秒激光辐照高粘性的金属玻璃Ti₄₀Zr₂₅Cu₁₂Ni₃Be₂₀ (%) 具有更广波纹范围的现象。粘性高的金属玻璃材料具有更小的波长和振幅, 波传播距离更远, 因此具有更为广阔的波纹范围。

3.等离子体与熔融金属玻璃材料相互作用影响波纹的形成, 不同等离子体条件, 如速度、密度和粘性, 对应不同的波数, 根据实验观测到不同位置的实际波数及液体粘性的数据可以反推相应位置等离子的参数。