电力电子装置周期性故障波形小波矩阵分类法
胡志坤1,徐 飞1,桂卫华2,安 庆3
(1. 中南大学 物理科学与技术学院,湖南 长沙,410083;
2. 中南大学 信息科学与工程学院,湖南 长沙,410083;
3. 河南周口市供电局,河南 周口,466001)
摘 要:提出一种基于平稳小波变换和奇异值分解的电力电子装置周期性故障波形的分类方法。该方法利用平稳小波变换的冗余性和奇异值的稳健性。其步骤为:对周期性故障波形进行平稳小波变换,将信号分解到多个小波子空间;将平稳小波变换后的小波系数矩阵奇异值进行分解,即采用K-L变换对子信号进行特征压缩,并以奇异值向量作为特征向量;按照向量的空间距离对故障波形进行分类实现故障的分类诊断。以精确的半导体器件模型建立的PSPICE逆变器故障波形为例,分别用该方法和小波子带能量法对逆变器的IGBT开关故障进行分类。研究结果表明,与采用小波子带能量法相比,采用所提方法能够精确地对22种逆变器断路故障进行诊断,且受小波分解层数的影响较小,分类边界较清晰,其类间距与类内距之比是小波子带能量法的2.5倍,抗噪性能好,正确识别率高5%。
关键词:平稳小波变换;奇异值分解;逆变器故障;分类
中图分类号:TM464 文献标识码:A 文章编号:1672-7207(2009)04-1015-07
Wavelet matrix classification for periodic fault wave of
power electron equipment
HU Zhi-kun1, XU Fei1, GUI Wei-hua2, AN Qing3
(1. School of Physics Science and Technology, Central South University, Changsha 410083, China;
2. School of Information Science and Engineering, Central South University, Changsha 410083, China;
3. Henan Zhoukou Power Supply Bureau, Zhoukou 466001, China)
Abstract: Wavelet matrix classification, which takes advantage of redundancy of the stationary wavelet transform and steadiness of singular value decomposition, was proposed in order to classify the periodic fault wave of power electron equipment. The procedures are as follows: Periodic fault wave is decomposed into sub-space by the stationary wavelet transform, singular value is obtained by singular value decomposition of wavelet coefficient matrix, and the essential of singular value decomposition is the decompressed by K-L transform. Classification was completed by calculating the space distance of two singular values. The fault wave, which was from the precise PSPICE model of inverter, was classified by the proposed method and the wavelet sub-band energy method. The results show that, compared with wavelet sub-band energy method, the proposed method can completely diagnose 22 on-off faults of inverter, the wavelet level has little effect on the proposed method, the classification borderline of proposed method is more clear, the distance of different kinds of proposed method is 2.5 times larger than wavelet sub-band energy method, and the correct recognition rate of proposed method is 5% higher than wavelet sub-band energy method.
key words: stationary wavelet transform; singular value decomposition; fault of inverter; classification
电力电子装置是许多工业生产过程的关键设备。实际运行结果表明,大多数故障表现为功率开关器件被损坏[1-2],导致电力电子装置的输出故障波形呈现周期性的特征。因此,可对故障波形进行分类,以实现快速准确地对故障定位。目前,电力电子装置故障波形特征提取方法主要是小波变换。小波变换能够提供多方位、多层次的动态分析能力,它不仅能够有效地表征原始特征信号而且大大压缩信号特征的维数[3]。小波细节系数和平滑系数实质上是一串时间序列,因此,即使是同一个样本波形,也会有较大的差异;另外,小波系数长度大于或者等于原波形序列的长度,因此,小波系数不适合用于直接表征原始波形的特征信息。采用小波子带能量[4-6]作为特征向量进行分类,其类距和抗干扰能力的效果不理想。小波边缘特征法虽然具有很高的特征表示能力,但是,因其维数过高导致分类器过于复杂,从而降低了其实用性[7]。通过奇异值分解结合快速傅里叶变换虽然能够反映矩阵固有的特征,并且具有良好的稳定性,但信号矩阵的构造相对复杂[8-10]。为此,本文作者利用平稳小波变换的良好波形数据表征能力和矩阵奇异值分解的稳定性,提出对电力电子装置因断路故障呈现的周期性波形进行分类的小波矩阵分类法,以实现对功率器件故障的快速定位。
1 波形特征值的提取
1.1 离散正交小交变换与平稳小波变换
离散正交小波变换[11]是一种非冗余的小波变换。它在离散框架的基础上构造正交基,并将离散数据映射到相互正交的子空间中,其多分辨率公式为:
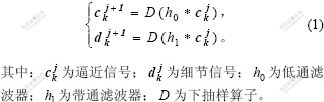
采用Mallet算法对离散正交小波变换进行计算,其运算量较小,但是,每经过一级变换,尺度数据长度减半,因此,尺度越大,越难以反映波形变化全貌。离散正交小波变换方法虽然具有一定的去相关作用,但是,它只是一种近似的K-L变换,不具备K-L变换特征的稳定性。
平稳小波变换是在正交小波变换基础上提出的一种冗余非正交小波变换方式。它将信号与低通滤波器卷积得到低频系数A1,与高通滤波器卷积得到高频系数D1。对于低频A1,使用同样的方法将其分成2部分,其分解图如图1所示。

(a) 信号分解过程;(b) 滤波器构造
图1 离散平稳小波变换
Fig.1 Discrete stationary wavelet transform
离散平稳小波变换加大了小波变换时间轴上的栅格密度,使得各级尺度上的细节信号和逼近信号的长度均等于原信号的长度。平稳小波变换的特点是冗余性和平移不变性,是连续小波变化更近似的估计,因此,各级尺度系数与正交小波变换能够更完整地反映波形变化的特征。
对于长度为N的离散故障波形信号x(n),经过L级离散平稳小波变换后取全部低频系数和第1层高频系数得到(L+1)×N的小波系数矩阵S:

由上述分析结果可知,矩阵S相对于离散正交小波变换得到的矩阵更能够完整地体现故障波形的 特征。
1.2 小波系数矩阵的奇异值分解
引理1

矩阵A经奇异值分解后可以表示为k个秩为1的m×n阶子矩阵ai之和:
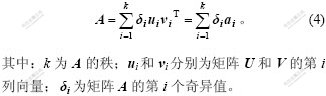 由于vi之间是两两正交,故
由于vi之间是两两正交,故
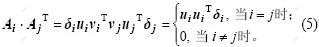
由式(4)和(5)和引理1可得出推论1。
推论1 矩阵奇异值分解是将矩阵分解到k个秩为1的正交子矩阵ai的子空间中,奇异值向量代表矩阵每个正交子空间的信息量。
引理2 对于矩阵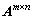 和
和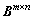 ,它们的奇异值 δ1≥δ2≥…≥δn,τ1≥τ2≥…≥τn,则:
,它们的奇异值 δ1≥δ2≥…≥δn,τ1≥τ2≥…≥τn,则:
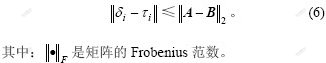
由引理2可知,当矩阵有微小的波动时,奇异值的改变不会大于矩阵之差的2范数,因此,可得出推论2。
推论2 矩阵经奇异值分解后,其奇异值向量具有很强的稳定性。
由推论1和推论2可得:矩阵奇异值分解是将矩阵分解到k个秩为1的正交子矩阵ai的子空间中,奇异值向量代表矩阵在每个子空间中的信息量,且具有良好的稳定性。
故障波形信号x(n)经过L级离散平稳小波变换,得到小波系数矩阵S,再经奇异值分解后的奇异值向量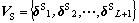 具有正交分解的去相关性、奇异值矢量的准确性和稳定性。
具有正交分解的去相关性、奇异值矢量的准确性和稳定性。
1.3 小波矩阵法波形特征值的提取
对于长度为N的离散电力波形信号x(n),其中 1≤n≤N,提取特征值的步骤如下。
a. 将信号x(n)延拓为长度符合平稳小波变换的信号x(n′)。
b. 对x(n′)一维信号进行L级离散,得到L+1行小波系数矩阵S。
c. 将小波系数矩阵S进行奇异值分解得到奇异值向量Vs。
2 逆变器故障模型及分类判定
2.1 采用PSPICE建立逆变器模型
以PSPICE作为整个系统分析的平台,采用ixgh24n60cd模型和三相线性负载建立逆变器的PSPICE模型,如图2所示[13-14]。
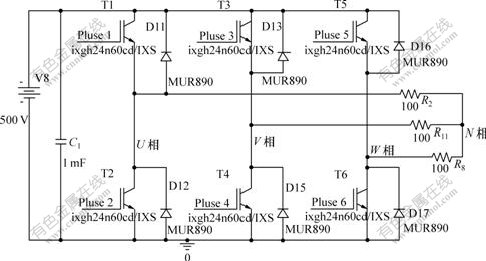
图2 PSPICE逆变器模型
Fig.2 Model of PSPICE inverter
2.2 逆变器故障样本分类
逆变器由6只绝缘栅双极型晶体管(IGBT)构成。为了简化分析过程,假定最多有2只IGBT同时开路,因此,逆变器单个线电压故障波形可分为正常情况、单管开路和双管同时开路3种类型共22种波形。其中,单管开路故障共6种,同桥臂双管开路故障共3种,不同桥臂双管开路故障共12种。将3种线电压共66种波形进行平稳小波变换,将奇异值分解得到奇异值向量。图3所示为66种波形经平稳小波和奇异值分解后奇异值向量的分类图。其中:δi为奇异值向量的第i个值。
由图3可知,3个线电压66种故障波形可以分为4类故障,表1所示为3个线电压对应故障的分类结果。
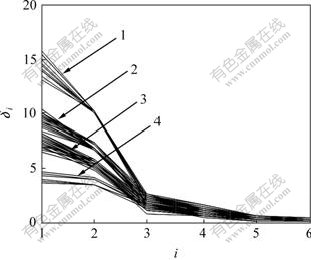
1—第1类故障;2—第2类故障;
3—第3类故障;4—第4类故障
图3 3个线电压故障特征向量分类曲线
Fig.3 Eigenvector classification curves of
three line-to-line voltages
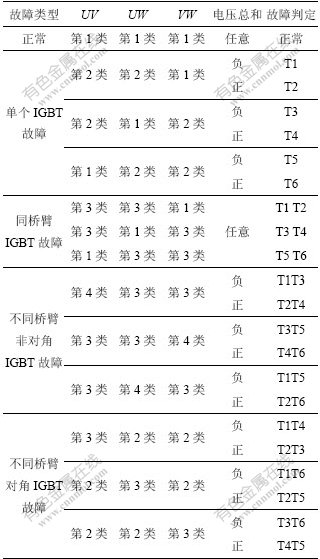
表1 3个线电压对应故障的分类
Table 1 Classification of three line-to-line voltages

注:U,V和W分别代表U相、V相和W相(见图2)。
2.3 逆变器故障的判定
由图3和表1中的分类方法,可对IGBT故障进行分类判定,其类型可分为正常运行、单个IGBT故障、同桥臂IGBT故障、不同桥臂非对角IGBT故障和不同桥臂对角IGBT共5种故障。
2.3.1 正常运行判定
逆变器正常工作,可直接由第1类判定。由表1可知,逆变器正常工作时的3个线电压经平稳小波变换和奇异值变换后,其3个线电压的特征向量都属于第1类。因此,当3个线电压都属于第1类时,可直接判定逆变器运行正常。
2.3.2 单个IGBT故障
逆变器的单个IGBT故障可由第1类和第2类判定。以T1发生故障为例,当T1发生故障时,VW线电压属于第1类,UV和UW线电压属于第2类。对照表1可知,T1或者T2发生故障。对3个线采样电压进行叠加,当其结果为负数时,表明T1发生故障;为正数时,表明T2发生了故障。
2.3.3 同桥臂IGBT故障
同桥臂IGBT故障可由第1类和第3类判定。以T1和T2同时发生故障为例,当T1和T2同时发生故障时,UV和UW线电压属于第3类,VW线电压属于第1类。结合表1可知,T1和T2同时发生故障。
2.3.4 不同桥臂非对角IGBT故障
不同桥臂非对角IGBT故障可由第3类和第4类判定。以T1和T3同时发生故障为例,当T1和T3同时发生故障时,UW和VW线电压属于第3类,UV线电压属于第4类,结合表1可得出T1T3或者T2T4发生故障。对3个线电压采样点进行叠加,当结果为负数时,表明T1T3发生故障;为正数时,表明T2T4发生了故障。
2.3.5 不同桥臂对角IGBT故障
不同桥臂对角IGBT故障可由第2类和第3类判定。以T1和T4同时发生故障为例,当T1和T4同时发生故障时,UW和VW线电压属于第2类,UV线电压属于第3类,结合表1可知,T1T4或者T2T3发生故障。对3个线电压采样点进行叠加,当结果为负数时,表明T1T4发生故障;为正数时,表明T2T3发生故障。
针对上述5类故障共22种,采用4类特征向量分类方法和三线采样电压总和可精确地判定其中任意 1种故障,三相逆变器IGBT故障判定结果如表2所示。因此,采用该方法能够准确判定22种IGBT故障。
3 小波矩阵法的仿真分析
3.1 小波分解层数仿真分析
针对小波矩阵法的分类性能,将小波矩阵法和小波子带能量法进行比较。首先,对66种故障波形采用db3小波分别进行3,4和5层小波分解,然后,对分解后的小波系数分别采用小波子带能量法和小波矩阵法进行处理,得到2种方法的4,5和6维特征向量集合。将4,5和6维特征向量集合分别压缩成2维向量集合,如图4所示。压缩方法是:取向量前2个元素的和为第1维;自向量第2个元素开始,后几个向量的和为第2维。
表2 逆变器IGBT故障的判定
Table 2 Diagnosis of IGBT fault of inverter
由图4(a)~(c)可知,小波子带能量法受到小波分解的层数影响较大,其在分解层数为3时效果较好,在分解层数为4时较难分类,在分解层数为5时基本不能分类。由图4(d)~(f)可知,小波矩阵法受分解层数影响较小,据其3个分解层数能清晰地将故障进行分类。
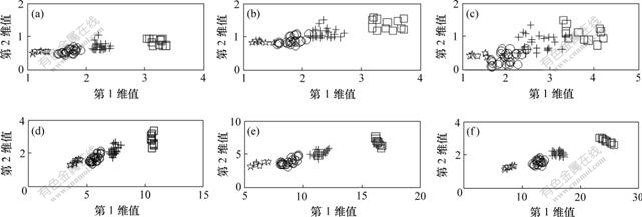
(a) 小波子带法3层分解;(b) 小波子带法4层分解;(c) 小波子带法5层分解;
(d) 小波矩阵法3层分解;(e) 小波矩阵法4层分解;(f) 小波矩阵法5层分解
□—第1类故障;+—第2类故障;○—第3类故障;☆—第4类故障
图4 分解层数对小波子带法与小波矩阵法的影响
Fig.4 Effects of decomposition level on wavelet sub-band energy method and wavelet matrix method
小波矩阵法与小波子带能量法相比,小波矩阵法受分解层数的影响较小。其原因是:小波子带能量法提取各层小波系数的能量,对于频率分量不同的波形,其选取的分解层数对结果有较大影响。例如,含低频分量较多的波形应采取较低的分解层数,对于高频分量较多的波形,当分解层数较高时,分类的效果更明显。小波矩阵法是对小波系数矩阵进行奇异值分解,它是一种K-L变换,其分解后的子空相互正交具有去相关作用。矩阵的奇异值向量代表子矩阵的系数,而子矩阵是小波系数矩阵的分量。由于它包含低频和高频的所有信息,因此,分解层数对小波矩阵法的影响较小。可见,小波矩阵法与小波子带能量法相比,具有更强的稳定性和实用性。
3.2 类距仿真分析
类距包含类内距和类间距,它是评价分类方法质量的有效方法。这里采用平均类内距和平均类间距对小波矩阵法和小波子带能量法进行比较分析。平均类内距和平均类间距为:

将66种故障波形分别叠加10种不同幅值的噪声,得到10组共660个样本。由图4可知,采用小波子带能量法在3层分解时效果最好。采用小波子带能量法和小波矩阵法分别对660个样本的db3小波3层和5层进行分析,所得2种方法各类的平均类内距、最大类内距、各类之间的类间距和和类间距如表3所示。
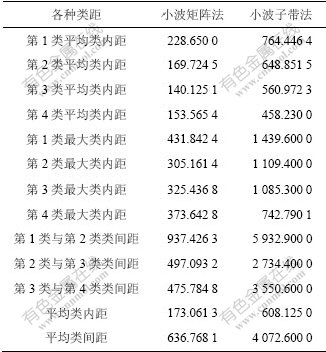
由表3可知,小波子带法的第2类最大类内距和第3类最大类内距之和为625,然而,第2类与第3类的类间距为497,因此,在第2类和第3类之间会有少部分数据出现判别不清楚现象。采用小波矩阵法,最大类内距之和为2 194,第2类与第3类的类间距为2 734,因此,小波矩阵法的分类在第2类与第3类之间不会出现误判问题。同理,在第3类与第4类中小波矩阵法的分类效果仍比小波子带能量法的好。小波矩阵法的平均类内距是小波子带能量法的3倍,而其平均类间距是小波子带能量法的7倍。因此。无论各类之间的分类效果还是整体上的平均分类效果,小波矩阵法都好于小波子带能量法。
表3 小波矩阵法与小波子带能量法的类距比较
Table 3 Comparison of distance between kinds
对于660个样本经过2种方法变换后的特征向进行二维压缩。小波矩阵法分类图和小波子带能量法分类图如图5所示。由图5可知,小波矩阵法的分类图更清晰,类与类之间的分类边界更明显,而小波子带能量法分类边界比较模糊,特别在第2类、第3类和第4类之间的区分更模糊,容易出现误判和错判。由图5可知,小波矩阵法比小波子带能量法具有更好的分类效果,也间接地说明小波矩阵法抗噪声能力要比小波子带能量法的抗噪声能力强。
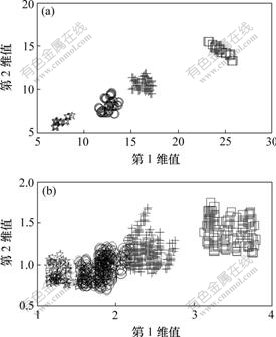
(a) 小波矩阵法;(b) 小波子带能量法
□—第1类故障;+—第2类故障;○—第3类故障;
☆—第4类故障
图5 2种方法的类距比较
Fig.5 Comparison of distances obtained by two methods
3.3 测试分析
将660个样本经过2种方法处理后的特征向量作为训练集,以最大类内距作为判定的距离,对于每一类随机抽取50个样本进行测试,测试结果如表4所示。
表4 小波矩阵法与小波子带能量法的识别率比较
Table 4 Comparison of correct recognition rates obtained by two methods
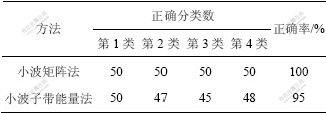
由表4可知,采用小波矩阵法所得的正确识别率与采用小波子带能量法相比提高了5%,其第2类、第3类和第4类的正确分类数都比采用小波子带能量法所得结果好。因此,小波矩阵法比小波子带能量法能更好地判定逆变器断路故障。
4 结 论
a. 采用小波矩阵分类法能够准确快速地对22种IGBT故障进行分类判定。
b. 与小波子带能量法相比,小波矩阵法受小波分解层数的影响较小。
c. 小波矩阵法的平均类内距是小波子带能量法的3倍,但其平均类间距是小波子带能量法的7倍,且小波矩阵法的分类边界比小波子带能量法的分类边界更清晰。
d. 采用小波矩阵法所得分类识别率比采用小波子带能量法所得分类识别率高5%。
参考文献:
[1] Peuget R, Courtine S, Rognon J P. Fault detection and isolation on a PWM inverter by knowledge-based model[J]. IEEE Transaction on Industry Application, 1998, 35(6): 1318-1326.
[2] Kai R, Friedrich W F. Performance of diagnosis methods for IGBT open circuit faults in voltage source active rectifiers[C]//IEEE PESC. Berlin, 2004: 4348-4354.
[3] 胡汉辉, 杨 洪, 潭 青, 等. 基于小波分析的见机故障诊断[J]. 中南大学学报: 自然科学版, 2007, 38(6): 1169-1173.
HU Han-hui, YANG Hong, TAN Qing, et al. Sintering fan faults diagnosis based on wavelet analysis[J]. Journal of Central South University: Science and Technology, 2007, 38(6): 1139-1173.
[4] 王 群, 倪宏伟, 徐毅刚. 基于小波能量特征的探雷方法研究[J]. 数据采集与处理, 2003, 18(2): 156-160.
WANG Qun, NI Hong-wei, XU Yi-gang. Mine detection and identification using wavelet analysis[J]. Journal of Data Acquisition & Processing, 2003, 18(2): 156-160.
[5] 孟永鹏, 贾申利, 荣命哲. 小波包频带能量分解在断路器机械状态监测中的应用[J]. 西安交通大学学报, 2004, 38(10): 1013-1017.
MENG Yong-peng, JIA Shen-li, RONG Ming-zhe. Application of frequency band energy decomposition using wavelet packet in condition monitoring of circuit breakers[J]. Journal of Xi’an Jiaotong University, 2004, 38(10): 1013-1017.
[6] HU Xiao, WANG Zhi-zhong, REN Xiao-mei. Classification of surface EMG signal using relative wavelet packet energy[J]. Computer Methods and Programs in Biomedicine, 2005, 79(3): 189-195.
[7] 王慧燕, 诸 静. 基于小波变换的边缘检测及在绝缘瓷瓶故障诊断中的应用[J]. 电力系统自动化, 2004, 28(15): 76-79.
WANG Hui-yan, ZHU Jing. Wavelet transform based edge detection and its application in porcelain bottles fault monitoring[J]. Automation of Electric Power Systems, 2004, 28(15): 76-79.
[8] Junying G, Youwei Z H. A study of singular value decomposition of face image matrix[J]. Neural Networks and Signal Processing, 2003, 1: 197-199.
[9] Akritas A G, Malaschonok G I. Applications of singular value decomposition(SVD)[J]. Mathematics and Computers in Simulation, 2004, 67(1): 15-31.
[10] 赵学智, 陈统坚, 叶邦彦. 基于奇异值分解的铣削力信号处理与铣床状态信息分离[J]. 机械工程学报, 2007, 43(6):169-174.
ZHAO Xue-zhi, CHEN Tong-jian, YE Bang-yan. Processing of milling force signal and isolation of state information of milling machine based on singular value decomposition[J]. Chinese Journal of Mechanical Engineering, 2007, 43(6): 169-174.
[11] Mallat S. A theory for multi resolution signal decomposition: the wavelet representation[J]. IEEE Trans Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693.
[12] Konsstantinides K, Yao K. Statistical analysis of effective singular values in matrix rank determination[J]. IEEE Trans on Acoustics, Speech and Signal Process, 1988, 36(5): 757-763.
[13] CHEN Shu-jun, WANG Jun, HUANG Peng-fei, et al. Simulation and experimentation of the arc welding inverter using the soft switching technique[J]. Chinese Journal of Mechanical Engineering, 2004, 17(1): 82-84.
[14] 苏 麟, 梅 军, 郑建勇, 等. PSPICE和Matlab在IGBT动态仿真中应用[J]. 电力自动化设备, 2004, 24(6): 58-61.
SU Lin, MEI Jun, ZHENG Jian-yong, et al. Application of PSPICE and Matlab in IGBT dynamic simulation[J]. Electric Power Automation Equipment, 2004, 24(6): 58-61.
收稿日期:2008-10-15;修回日期:2009-01-20
基金项目:国家自然科学基金重点资助项目(60634020);湖南省自然科学基金资助项目(06FD007);博士后科学基金资助项目(20060400885)
通信作者:胡志坤(1976-),男,湖北鄂州人,博士,副教授,从事电力电子变流技术研究;电话:0731-88830394;E-mail: huzk@mail.csu.edu.cn