J. Cent. South Univ. Technol. (2011) 18: 791-799

DOI: 10.1007/s11771-011-0764-9

Novel algorithm for geomagnetic navigation

LI Ming-ming(李明明), LU Hong-qian(卢鸿谦), YIN Hang(尹航), HUANG Xian-lin(黄显林)

Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: To solve the highly nonlinear and non-Gaussian recursive state estimation problem in geomagnetic navigation, the unscented particle filter (UPF) was introduced to navigation system. The simulation indicates that geomagnetic navigation using UPF could complete the position estimation with large initial horizontal position errors. However, this navigation system could only provide the position information. To provide all the kinematics states estimation of aircraft, a novel autonomous navigation algorithm, named unscented particle and Kalman hybrid navigation algorithm (UPKHNA), was proposed for geomagnetic navigation. The UPKHNA used the output of UPF and barometric altimeter as position measurement, and employed the Kalman filter to estimate the kinematics states of aircraft. The simulation shows that geomagnetic navigation using UPKHNA could provide all the kinematics states estimation of aircraft continuously, and the horizontal positioning performance is better than that only using the UPF.

Key words: autonomous navigation; geomagnetic navigation; unscented particle filter; Kalman filter; kinematics state estimation

1 Introduction

Accuracy and robustness are vital to aircraft navigation, both in the military and civil. Most navigation systems are built around the strapdown inertial navigation system (SINS). SINS could provide the position, velocity and attitude of aircraft continuously, but has an unbounded growth in the position and velocity errors. Therefore, other techniques have been developed to reduce the navigation errors. The best known technique is the SINS/GPS integrated navigation. However, GPS signals are extremely vulnerable to be interfered even lost. When GPS measurements are unavailable, SINS begin to drift out of calibration, and the navigation accuracy quickly degrades to an unacceptable level.

Recently, some novel navigation technologies with geophysical field reference, for instance geomagnetic filed, gravity field and terrain field, have been proposed to eliminate the cumulated error of SINS [1]. The terrain-aided navigation algorithms have been reported to be successful in many applications. However, when flying over fairly flat, for example the water-covered areas, the terrain-aided navigation cannot be applied because of the irresolvable ambiguities in terrain map. And the terrain-aided navigation is not an autonomous mode, since an active apparatus, such as a radio altimeter, is used, which transmits radio signals and makes the aircraft vulnerable especially during high altitude flights. The concept of geomagnetic navigation was first proposed by CARL in 1982 [2], and attracted more attention recently [3-7]. As mentioned in Ref.[1], the geomagnetic field can be used as reliable navigation reference on at least 98% of the earth surface and near earth space, including water-covered surface. Furthermore, the geomagnetic navigation works with radio-passive apparatus, such as a magnetometer, thereby improving the aircraft resistance to radio intelligence, and making the aircraft have a complete autonomous navigation. Therefore, the geomagnetic navigation could satisfy the requirements of passive, anti-jam and miniature navigation system.

Here, geomagnetism is used to estimate the drift of SINS. The geomagnetic navigation is also map-matching navigation, thus many algorithms have been used by terrain-aided navigation and other map-matching navigations could also be applied [5-10], such as TERCOM, iterative closest contour point (ICCP), extended Kalman filter (EKF), and particle filters (PF). However, these algorithms all have their own limitations. Consequently, in this work, a recursive estimation algorithm called unscented particle filter (UPF) [11] is introduced to solve the nonlinear recursive estimation problem in geomagnetic navigation. And a novel autonomous navigation algorithm for geomagnetic navigation system based on UPF and Kalman filter is proposed.

2 Map-matching navigation algorithm

Due to the nonlinearity of map-matching navigation, Kalman filter cannot be used directly. There are several algorithms that could solve the nonlinear problem in map-matching navigation. These algorithms could be divided into two parts: batch and sequential.

In the batch processing, a series of measurements are processed together. The famous algorithms are TERCOM [5] and ICCP. The TERCOM matches the measurements with the database in map at different offsets from current estimated position in latitude and longitude. And the offsets which have the maximum likelihood are regarded as the position errors. But the aircraft is not allowed to maneuver during data acquisition in the TERCOM and this algorithm is sensitive to heading errors. The BEHZAD introduced the ICCP algorithm into the map-matching navigation in 1999 [12]. The major idea of the ICCP is to regard the estimation position of SINS and the real track as two curves on map, and compute the rigid transformation. It does not require the aircraft to maintain straight-line motion. However, when the positioning errors are large and the map data are strong correlation, the ICCP is easy to converge to the local minimum [6].

In the sequential processing, each measurement is processed separately. SITAN is a typical sequential processing algorithm, which uses EKF to deal with the nonlinear problem. The aircraft with the SITAN could maneuver the flight. However, for nonlinear system, the EKF must linearize the nonlinear model by calculating the gradient, which is calculated using the estimation position of the navigation system, not the true position. Therefore, when the position error is large or the gradient has dramatic variety, the SITAN may be divergent [7]. Furthermore, the map-matching navigations usually have non-Gaussian noise, deal with which the EKF often provides a solution far from being acceptable. Another technique is PF [10]. The PF also takes a recursive approach, but without the linear/Gaussian assumptions. Therefore, the map-matching navigation using the PF allows aircraft to maneuver and could be applied with large position errors. The PF is fitted to the posterior distribution for estimation, instead of being fitted to the likelihood function. And the more the nonlinear system, or the more the non-Gaussian noise, the more advantage the PF has. In Ref.[13], the point-mass filter and the bootstrap filter (one kind of PF) have been applied to estimate the aircraft position, respectively. But, other kinematics states of aircraft could not be estimated. All the kinematics states have been estimated in Ref.[14] using the Rao-Blackwellized particle filter (one kind of PF), but some elements in navigation equation have been neglected. And the performance of navigation system may be affected by this simplification. On the other hand, the PF in Refs.[13-14] uses prior distribution as the importance proposal distribution to generate particles, without incorporating the most recent measurements. This kind of PF is especially sensitive to outliers and may cause a large error if there is little overlap between prior and posterior probability [15].

To overcome the problem of above algorithms used in map-matching navigation, UPF is introduced to geomagnetic navigation, which generates the importance proposal distribution using the most recent measurements. And a novel navigation algorithm, named unscented particle and Kalman hybrid navigation algorithm (UPKHNA), is proposed, which could estimate all the kinematics states without simplifying the navigation equation.

3 Geomagnetic navigation using UPF

3.1 Problem description

The estimation problem associated with the geomagnetic navigation is to match the measurements of geomagnetism with the geomagnetic reference map. The geomagnetism value varies with the horizontal position and the altitude of aircraft. Assuming additive measurement noise, the geomagnetism measurement value y_k relates to the current aircraft horizontal position x_k and altitude h_k according to

y_k=h(x_k, h_k)+e′_k                                    (1)

The barometric altimeter is often used in conjunction with SINS. This integration can produce unbiased estimation of altitude and limit the vertical channel errors of SINS in several tens of meters. Therefore, Eq.(1) can be rewritten as

y_k=h(x_k)+e_k                                       (2)

where the function h(?) is the geomagnetic reference map. e_k is the noise with probability density function 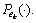 e_k models both the errors in magnetometer, and the errors caused by altitude error and geomagnetic reference map not perfectly resembling the actual geomagnetism value.

The relative movements of aircraft, u_k, between two measurements are estimated by SINS. The absolute movements of aircraft satisfy a simple linear equation:

x_k=x_k-1+u_k+v_k                                      (3)

where v_k denotes the drift of SINS with the probability density function

Summarizing Eq.(2) and Eq.(3), the geomagnetic navigation equation is obtained:

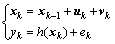                              (4)

where e_k and v_k are mutually independent white processes and both of them are uncorrelated with the initial position x₀, which has a distribution according to P(x₀).

The aim of geomagnetic navigation algorithm is to estimate the current aircraft position x_k through the observations Y_1:k={y₁, …, y_k}. Because the function h(?) is nonlinear and nonanalytical, using the unscented particle filter for estimation is a feasible way.

3.2 UPF algorithm for geomagnetic navigation

The UPF could provide a solution to the nonlinear and non-Gaussian filtering problem with no restriction to the state and noise distribution. It uses the unscented Kalman filter (UKF) to generate the importance proposal distribution. Since the UKF could incorporate the observation well and propagate the mean and the covariance of state distribution accurately [16], the important proposal distribution of UPF will have more overlap with the true posterior distribution than other PFs. Therefore, the UPF will perform better than other PFs [11]. The UPF algorithm is introduced to solve the nonlinear and non-Gaussian problem in geomagnetic navigation.

The geomagnetic navigation equation is built as Eq.(4), and UPF is adopted to estimate the aircraft horizontal position x_k recursively. The navigation structure diagram is shown in Fig.1.

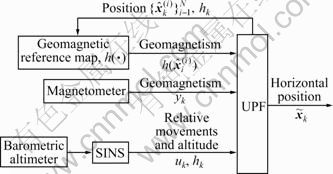
Fig.1 Illustration of geomagnetic navigation using UPF

The UPF algorithm for geomagnetic navigation used in this work can be described as follows.

Step 1 Initialization (k=0)

Draw N particles (samples) 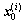 from the initial horizontal position prior distribution P(x₀), and set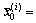 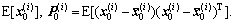 Assign the particles weights 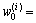1/N (i=1, 2, …, N).

For k=1, 2, …, ∞, begin the loop.

Step 2 Importance sampling

1) For each particle 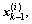 use Eq.(4) and the UKF algorithm to update them with covariance  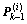and the most recent observation y_k. Obtain mean  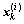and covariance  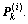The UKF algorithm can be referred to Ref.[16] for detail.

2) Set the importance proposal distribution function 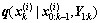 to be equal to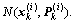

3) Sample 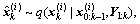 then get new particles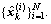

Step 3 Weights updating

The importance weights can be updated as

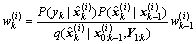
where

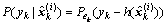                              (5)

                          (6)

Normalize the weights as

Step 4 Resampling

1) Evaluate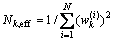

2) If 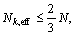 make residual resampling, and

set weights 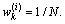 The residual resampling scheme can be referred to Ref.[17] for detail.

Step 5 Output

The minimum mean square estimation (MMSE) of x_k and covariance are calculated as

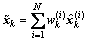                                    (7)

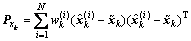                         (8)

During the implement of UPF, it may produce a particle degeneracy phenomenon. In Step 4, the residual resampling scheme is applied to reduce the degeneracy phenomenon. Other efficient resampling schemes in Ref.[18] could also be applied. However, the specific choice of resampling scheme does not significantly affect the performance of UPF [11].

Since the computational complexity of the algorithm increases dramatically with the dimension of state space, the UPF cannot solve high dimensional real-time estimation problems. However, the state dimensions of Eq.(4) are only two and the state equation of Eq.(4) is linear. Therefore, the computational complexity of UPF used in geomagnetic navigation could be small.

3.3 Performance of geomagnetic navigation using UPF

To validate the feasibility of the geomagnetic navigation using the UPF, simulations are performed. The geomagnetic reference map used in these simulations is stored with a uniform grid of 100 m resolution, which is obtained through linear interpolation on a part of North American geomagnetic database [19]. The true simulated flight track is shown in Fig.2, and the axes are labeled in grid. The maneuvers are simulated as turns.

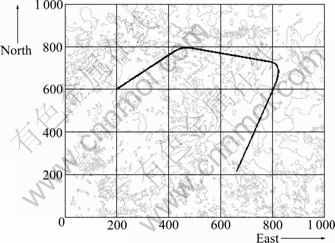
Fig.2 Simulation track over geomagnetic reference map

The track has duration of 550 s. And the magnetometer is sampled at a rate of 1 Hz. The SINS initial position x₀ has 1 000 m errors in both north and east direction, and the prior distribution is a Gaussian distribution with

P(x₀)=N(x₀, 1 000²I₂)                                (9)

The distributions used in simulation to model the process noise and measure noise in Eq.(4) are  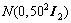 and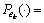N(0, 0.1²), respectively. The choice of the Gaussian distributions has been proven successful in simulations. But in practice, the distributions  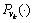and 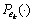 are all not Gaussian. Any other suitable distributions which could better model the noise should be used in practice. There is no restriction to Gaussian noise in the UPF. The only assumption is that the noise can be regarded to be white.

One hundred Monte Carlo simulations are performed with the number of particles N=10 000, and the results are given in Table 1.

Table 1 Simulation results of geomagnetic navigation using UPF

The root mean square error (RMSE, E) is calculated as

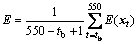                               (10)

where t_b is the time of filter convergence, and

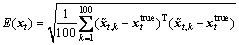            (11)

Figure 3 plots the position E(x_t) of geomagnetic navigation using the UPF in the north and east directions. From Table 1 and Fig.3, using the UPF for geomagnetic navigation could complete the horizontal positioning task, even in the case of large initial horizontal position errors.

The horizontal position RMSE is plotted in Fig.4. It is shown that there are two large error peaks in 115-143 s and 380-420 s, respectively. The first one is caused by the small geomagnetism value difference in the flight area, which even reaches the measurement noise level. So, it makes the measurement information little, and then makes the estimation error large. The second large errors in 380-420 s are caused by the phenomenon that the accelerations are changed greatly during the second turn maneuvers, which makes the errors of u_k in Eq.(4) much larger than other times.

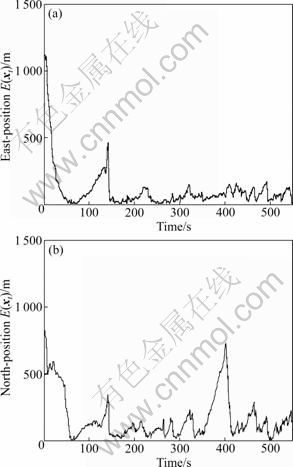
Fig.3 Position RMSE of geomagnetic navigation using UPF:  (a) East-position E(x_t); (b) North-position E(x_t)

Fig.4 Position RMSE of geomagnetic navigation using UPF in horizontal direction

In fact, choosing a large number of particles is used to overcome the large initial position errors and great maneuvers. With small errors and without maneuver, N could be chosen to be small to reduce the computational complexity and increase the real-time quality of algorithm. The simulations with initial errors of 100 m in both the north and east directions, in the flight along a straight-line and N=200 are also performed. The position RMSE curve is plotted in Fig.5. It is shown that the geomagnetic navigation system using the UPF could estimate the position well in this case, with N of only 200. Therefore, to reduce the computational complexity, an adaptive choice algorithm for N could also be applied in the UPF for the geomagnetic navigation.

4 Geomagnetic navigation using UPKHNA

The algorithm proposed could estimate the position of aircraft. However, a navigation system needs to estimate accurately not only the position, but also the velocity, attitude and even accelerometer and gyro errors. So, a novel navigation algorithm, UPKHNA, is proposed for geomagnetic navigation to solve this problem.

The UPKHNA framework for the geomagnetic navigation is shown in Fig.6. The barometric altimeter is used to provide the altitude measurement of aircraft. And the output of UPF (this algorithm is geomagnetic navigation using UPF algorithm, and can be found in Section 3 for detail) is used to provide the north and east direction position measurements of aircraft. These three- dimensional position measurements and kinematics states of aircraft from the SINS are fused in the Kalman filer to estimate the SINS errors. The error estimations are fed back to SINS to compensate the drift of SINS, and all the kinematics states are output from the Kalman filter.

From Fig.6, it is shown that the UPKHNA divides the geomagnetic navigation into linear part and nonlinear part without any simplification. Because of the function h(?), the horizontal position estimation is a nonlinear and non-Gaussian state estimation problem. In UPKHNA, UPF is adopted to estimate the aircraft horizontal position and the true aircraft horizontal position could be represented by Gaussian distribution 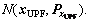 Then, the navigation equation becomes linear. The Kalman filter could be adopted to estimate the kinematics state errors of aircraft, by applying the horizontal position x_UPF and the altitude h_baro as measurements.

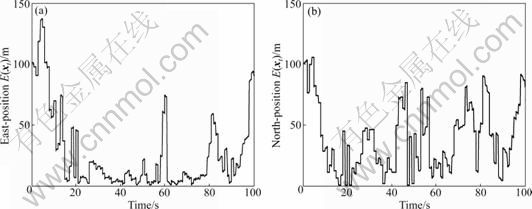
Fig.5 Position RMSE of geomagnetic navigation using UPF with small initial errors and N=200: (a) East-position E(x_t); (b) North- position E(x_t)

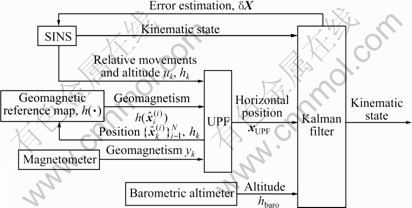
Fig.6 Illustration of geomagnetic navigation using UPKHNA

The navigation model in the UPKHNA for the geomagnetic navigation has two parts. The navigation model in the UPF is shown as Eq.(4). The navigation model in the Kalman filter can be described as follows:

1) State equation

In this navigation system, the system state, δX, is defined as the kinematics state errors and the accelerometer and gyro drift errors:

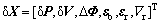                       (12)

where δP, δV denote the position errors and velocity errors along the east, north and up directions, respectively. ΔΦ denotes the attitude error. ε_b, ε_r and  denote the gyro bias, gyro random walk and accelerometer random walk along the east, north and up directions, respectively. The system state equation can be found in Ref.[20] and it is a linear equation.

2) Measurement equation

The measurement equation can be divided into two parts. One is the altitude measurement, h_baro~ 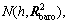 from the barometric altimeter, where h is the true altitude of aircraft. Another is the east and north position measurement from the UPF, x_UPF, which could be calculated from Eq.(7). And the variance  could be calculated approximately as Eq.(8). Then, the measurement equation could be obtained:

                            (13)

where

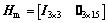
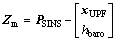
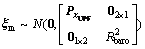
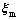 is the measurement noise and it is also linear. Therefore, the navigation system could apply the Kalman filter to estimate directly.

Through compensating the drift of SINS, the relative movement input of UPF in the UPKHNA, u_t in Eq.(4), is more accurate. Then, the divergence probability of UPF would be decreased and the horizontal position estimation precision from the UPF could be increased, which means that the position measurements of Kalman filter in the UPKHNA are more accurate. Then, the estimation performance of Kalmen filter will be enhanced. Furthermore, since the Kalman filter can fuse all the information together, even including the accelerometer and gyro drift, the horizontal position estimation errors of UPKHNA will smaller than those only using the UPF.

5 Simulation

To evaluate the performance of UPKHNA proposed, 100 Monte Carlo simulations are performed. The geomagnetic reference map, simulation flight track and noise distribution in Eq.(4) are the same as those in Section 3. The number of particles in UPF is N=10 000. Initialization data of simulation are listed in Table 2. The error source parameters are listed in Table 3.

Table 2 Initialization data of simulation

Table 3 Error sources parameters of simulation

The simulation results are given in Table 4. RMSE is calculated as Eq.(10). Figs.7-9 show the kinematics states RMSE along the simulation track using the UPKHNA.

Table 4 Simulation results of UPKHNA

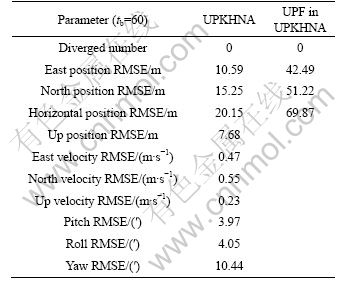
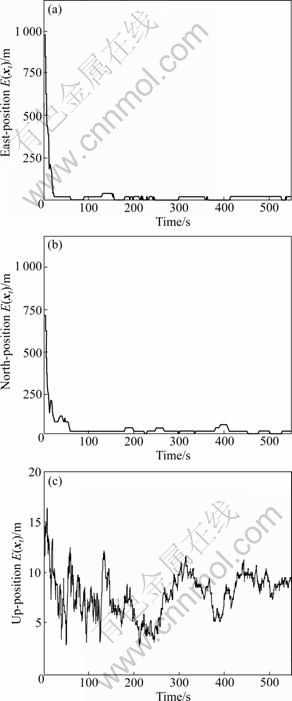
Fig.7 Position RMSE of geomagnetic navigation using UPKHNA: (a) East-position E(x_t); (b) North-position E(x_t);   (c) Up-position E(x_t)

The simulations show that the geomagnetic navigation using the UPKHNA could complete the navigation task in the case of large initial horizontal position errors. And the navigation algorithm is able to estimate all the navigation states of aircraft continuously. From Table 4, the positioning performances of UPKHNA are much better than those of the UPF in the UPKHNA. The largest average position errors and velocity errors along east and north directions are only 15.25 m and  0.55 m/s, respectively. The divergence of attitude could also be controlled well and the average attitude errors could reach the arcminute level.

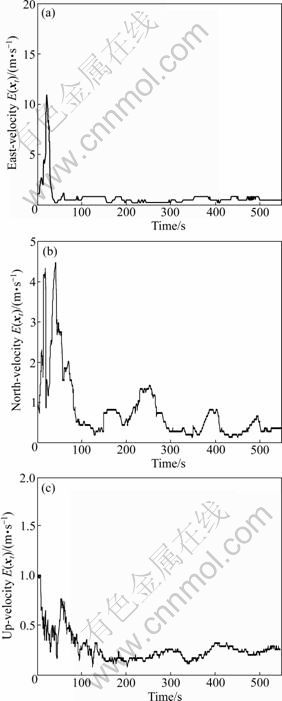
Fig.8 Velocity RMSE of geomagnetic navigation using UPKHNA: (a) East-velocity E(x_t); (b) North-velocity E(x_t);   (c) Up-velocity E(x_t)

By comparing Table 1 with Table 4, even the positioning performances of UPF in UPKHNA are much better than those only using the UPF. Figure 10 plots the geomagnetic navigation horizontal position RMSE using the UPKHNA, UPF in the UPKHNA and only UPF, respectively. It is shown that compared with that only using the UPF, the error of UPF in the UPKHNA is smaller and the RMSE curve has only one peak. This is due to the fact that the first large position error in 115-143 s is resulted from the small difference of geomagnetism value, which could not be avoided by the UPF. However, the second large position error in 380-420 s is caused by the large errors of u_t in Eq.(4). Through compensating the drift of SINS, the errors of u_t could always be small even during the maneuvers with large acceleration change. Therefore, the UPF in the UPKHNA could have a better positioning performance, even during 380-420 s. It should be noted that the first large error in the UPKHNA is also eliminated. This is because when the aircrafts fly over these small geomagnetism value difference areas, the position estimation performance of UPF is not well, leading to the large variance  calculated from Eq.(8). Then, through the fusion of Kalman filter in the UPKHNA, the effect of UPF large estimation errors on the navigation performance will be reduced. Furthermore, since Kalman filter can fuse all the information together, as shown in Fig.10, the estimation errors are the least and the error curve is the smoothest by using the UPKHNA.

Fig.9 Attitude RMSE of geomagnetic navigation using UPKHNA: (a) Pitch E(x_t); (b) Roll E(x_t); (c) Yaw E(x_t)

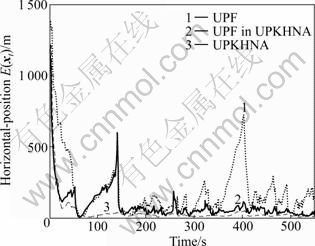
Fig.10 Horizontal position RMSE comparison

6 Conclusions

1) A recursive filtering algorithm, UPF, is applied in the geomagnetic navigation for solving the nonlinear and non-Gausses problem. The simulation results indicate that the geomagnetic navigation using the UPF could complete the navigation positioning task.

2) To provide all the kinematics states of aircraft, a novel autonomous navigation algorithm, named UPKHNA, for geomagnetic navigation, is proposed. It could complete the autonomous navigation task under large initial horizontal position errors, and provide all the kinematics state estimation continuously. Theoretical analyses and simulations show that geomagnetic navigation using the UPKHNA could estimate the navigation errors of SINS commendably, and the horizontal positioning performance is better than that only using the UPF.

3) It should be noted that even though the application area considered in this work is geomagnetic navigation, the UPKHNA proposed here could also be applied to other map-matching navigations.

References

[1] FELIX G. Geomagnetic navigation beyond the magnetic compass [C]// PLANS. San Diego, California, 2006: 684-694.

[2] CARL T. Magnetic anomalies as a reference of ground-speed and map-matching navigation [J]. Journal of Navigation, 1982, 35(2): 242-254.

[3] GUSAROV A. LEVRON D, PAPERNO E, SHUKER R, BARANGA A B. Three-dimensional magnetic field measurements in a single SERF atomic-magnetometer cell [J]. IEEE Transactions on Magnetics, 2009, 45(10): 4778-4481.

[4] CRASSIDIS J L, LAI, HARMAN R R. Real-time attitude-independent three-axis magnetometer calibration [J]. Journal of Guidance, Control, and Dynamics, 2005, 28(1): 115-150.

[5] FENG Hao-nan, YANG Zhao-hua, FANG Jian-cheng. Simulation design of geomagnetic aided inertial navigation system [C]// Proceeding 2nd International Symposium on Systems and Control in Aerospace and Astronautics. Shenzhen, China, 2008: 1-5.

[6] LUO Shi-tu, WANG Yan-ling, LIU Yin, HU Xiao-ping. Research on geomagnetic matching technology based on improved ICP algorithm [C]// Proceedings of the 2008 IEEE International Conference on Information and Automation. Zhangjiajie, China, 2008: 815-819.

[7] MU Hua, WU Mei-ping, HU Xiao-ping, MA Hong-xu. Geomagnetic surface navigation using adaptive EKF [C]// 2007 2nd IEEE Conference on Industrial Electronics and Applications. Harbin, China, 2007: 2821-2825.

[8] GROVES P D, HANDLEY R J. Optimising the integration of terrain referenced navigation with INS and GPS [J]. The Journal of Navigation, 2006, 59: 71-89.

[9] TONG Xiao-hua, WU Song-chun, WU Shu-qing, LIU Da-jie. A novel vehicle navigation map-matching algorithm based on fuzzy logic and its application [J]. Journal of Central South University of Technology, 2005, 12(2): 215-219.

[10] GUSTAFSSON F, GUNNARSSON F, BERGMAN N, FORSSELL U, JANSSON J, KARLSSON R, NORDLUND P J. Particles filters for positioning, navigation, and tracking [J]. IEEE Transactions on Signal Processing, 2002, 50(2): 425-437.

[11] MERWE R V D, DOUCET A, FREITAS N D, ERIC W. The unscented particle filter [D]. Cambridge: Cambridge University, 2000: 1-45.

[12] BEHZAD K P, BEHROOZ K P. Vehicle location on gravity maps [C]// Conference on Unmanned Ground Vehicle Technology. Orlando, Florida, 1999: 182-191.

[13] BERGH A K, ODDVAR H. Terrain aided underwater navigation using point mass and particle filters [C]// IEEE PLANS, Position, Location, and Navigation Symposium. San Diego, CA, United States, 2006: 1027-1035.

[14] NORDLUND P J, GUSTAFSSON F. Sequential Monte Carlo filtering techniques applied to integrated navigation systems [C]// Proceedings of the American Control Conference. Arlington, VA, United States, 2001: 4375-4380.

[15] DOUCET A, GODSILL S, ANDRIEU C. On sequential Monte Carlo sampling methods for bayesian filtering [J]. Statistics and Computing, 2000(10): 197-208.

[16] JULIER S J, UHLMANN J K, DURRANT-WHYTE H F. A new approach for the nonlinear transformation of means and covariances in linear filters [J]. IEEE Transactions on Automatic Control, 2000, 5(3): 477-482.

[17] LIU J S, CHEN R. Sequential monte carlo methods for dynamic systems [J]. Journal of the American Statistical Association, 1998, 93: 1032-1044.

[18] DOUC R, CAPPE O, MOULINES E. Comparison of resampling schemes for particle filtering [C]// Proceedings of the 4th International Symposium on image and Signal Processing and Analysis. Zagreb, Croatia, 2005: 64-69.

[19] U.S. Geological Survey. Digital data grids for the magnetic anomaly map of North America: U.S. Geological Survey Open-File Report 02-414 [R]. U.S. Geological Survey, Denver, Colorado, USA, 2002.

[20] HU Xiao-ping. Principles and applications of autonomous navigation [M]. Changsha: Press of National University of Defense Technology, 2002. (in Chinese)

(Edited by YANG Bing)

Foundation item: Project(HIT.NSRIF.2009006) supported by the Fundamental Research Funds for the Central Universities of China

Received date: 2010-07-29; Accepted date: 2010-11-24

Corresponding author: LI Ming-ming, PhD candidate; Tel: +86-451-86402204-8666; E-mail: liming20003@163.com