Trans. Nonferrous Met. Soc. China 22(2012) 1190-1196

Characteristic atom sequences of Nb-Mo alloys system in BCC structure and properties of disordered alloys

PENG Hong-jian^1,2, WU Qing¹, LI Xiao-bo², XIE You-qing²

1. School of Chemistry and Chemical Engineering, Central South University, Changsha 410083, China;

2. School of Materials Science and Engineering, Central South University, Changsha 410083, China

Received 16 March 2011; accepted 20 February 2012

Abstract: Comprehensively considering energy, volume and electronic structure of alloys, the ninth equation was determined as the interaction function of Nb-Mo alloys system in BCC structure on the basis of idea of systematic science of alloys, experimental lattice constants and heats of formation of disordered Nb_(1-x)Mo_x alloys. The structural parameters and properties of Nb and Mo characteristic atoms sequences and corresponding characteristic crystals sequences were determined in Nb-Mo alloys system. The electronic structure and physical properties of disordered Nb_(1-x)Mo_x alloys system were calculated according to concentration of characteristic atoms of disordered alloys. The change trend of physical properties is the same as that of electronic structure.

Key words: Nb-Mo alloys system; characteristic atom sequences; disordered alloys; properties

1 Introduction

The target of material science development is to continuously design and develop new materials to meet modernization and future needs. To develop material design by multi-structure levels and various properties, materials science should be systematic. After nearly thirty years of efforts, XIE et al [1-12] had established the framework of systematic science of alloys on the basis of energy band theory, valence bond theory and statistical thermodynamics. The core is the theory of the characteristic crystals and points out direction of alloy design. The theory has been successfully applied to Ag-Cu alloys [1-4] and Au-Cu alloys [5-8] in FCC structure, Ti-Al alloys with coexistence of FCC and HCP structures [9-12].

However, there is little research on alloys in BCC structure by the theory. The purpose of the present work is to choose Nb-Mo alloys in BCC structure as research subject. Based on the experimental lattice constants, heats of formation of disordered Nb_(1-x)Mo_x alloys and the theory of the characteristic crystals, comprehensively considering the energy, volume and electronic structure of alloys, the optimum equation was determined as the interaction function of Nb-Mo alloys system. The structural parameters and properties of Nb and Mo characteristic atoms sequences and corresponding characteristic crystals sequences in Nb-Mo alloys system were determined. According to the concentrations of the characteristic atoms, the structural parameters and properties of disordered Nb_(1-x)Mo_x alloys were obtained. The framework of systematic science of alloys will be further developed and improved.

2 Models and laws

In the disordered solid solution, the concentrations of characteristic atoms are, respectively

                          (1)

where 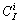 is the combination factor I!/[(I-i)!i!].

The average atomic energy of the alloys is

    (2)

The average atomic energies of components are, respectively

                         (3)

                         (4)

Substituting relations of property of characteristic crystals of component A and i into Eq. (4), three relations of average property q_A of component A with composition x_A can be obtained (the derivation is omitted here):

For type I,

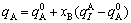;                       (5)

For type II,

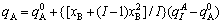          (6)

For type III,

       (7)

Similarly, three relations of average property q_B of component B with composition x_B can be obtained (the derivation is omitted here):

For type I,

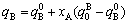;                       (8)

For type II,

          (9)

For type III,

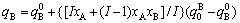      (10)

Combining the above equations and substituting them into Eq. (2), nine equations of average atomic potential energy and average atomic volume of solid solution can be obtained(see Table 1). For alloys system in BCC structure, I=8.

2.1 Determination of cohesive energies of Nb and Mo characteristic crystals of Nb-Mo alloys system in BCC structure

The crystalline structure of pure metals Nb and Mo is the same as that of Nb-Mo solid solutions.  and refer to cohesive energies of pure metals Nb and Mo, respectively.andare calculated by interaction equations of binary disordered alloys [13] from heats of formation [14] of Nb_(1-x)Mo_x solid solutions with different compositions. The results are listed in Table 2.

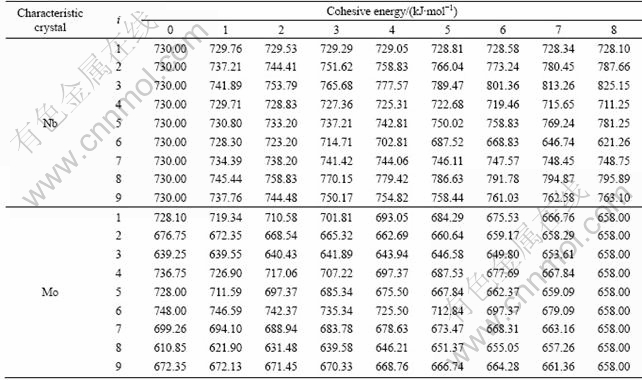
If we only consider the energy of disordered Nb_(1-x)Mo_x  alloy system in BCC structure, not average energy of every characteristic crystal, nine interaction equations are feasible in Table 1. The cohesive energies of the terminal state characteristic crystals are different from various equations. The cohesive energies of characteristic crystals by nine equations are listed in Table 3.

Table 1 Interaction equations of binary disordered alloys  (q=E, v)

Table 2 Terminal and primary values of cohesive energies of Nb and Mo characteristic crystals of Nb-Mo alloys system

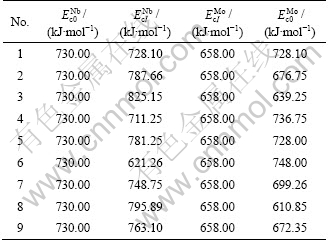
Table 3  Cohesive energies of characteristic crystals Nb and Mo of Nb-Mo alloys system by nine interaction equations

2.2 Determination of lattice constants of characteristic crystals Nb and Mo of Nb-Mo alloys system in BCC structure

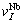The crystalline structure of pure metals Nb and Mo is also the same as that of Nb-Mo solid solutions.  and  refer to atomic volumes of pure metals Nb and Mo, respectively.  and 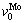 are calculated by volume interaction equations of binary disordered alloys from experimental lattice constants [15] of Nb_(1-x)Mo_x solid solutions with different compositions. The results are listed in Table 4.

If we only consider the atomic volumes of disordered Nb_(1-x)Mo_x  alloys system in BCC structure, not average atomic volumes of every characteristic crystal, nine interaction equations are also feasible in Table 1. The atomic volumes of the terminal state characteristic crystals are different from various equations. The lattice constants of Nb and Mo characteristic crystals by nine equations are listed in Table 5.

The research on energy and volume interaction equations of alloys indicates that primary values are the same by different interaction equations. But cohesive energies of different characteristic crystals have great differences by different interaction equations. Therefore, every interaction equation describes a specific interaction essence of Nb and Mo atoms in the theory of characteristic crystals and reflects microscope essence of solid solution. It is incorrect that the interaction equations are chosen only from alloy energy as a function of composition. Only considering the relationship among energy, volume, atomic state of alloy, the correct interaction equation can be chosen. The ninth equation is determined as interaction equation of disordered Nb_(1-x) Mo_x alloys by systematic analysis of properties of characteristic crystals in Tables 3 and 5.

(11)

where  =730 kJ/mol,  =658 kJ/mol, = 763.10 kJ/mol, =672.35 kJ/mol, I=8.

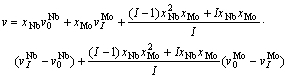(12)

where =0.0179750 nm³,=0.0155893 nm³, 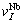 =0.0175250 nm³, 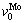=0.0153085 nm³, and I=8.

Table 4 Terminal and primary values of volume of Nb and Mo characteristic crystals of Nb-Mo alloys system

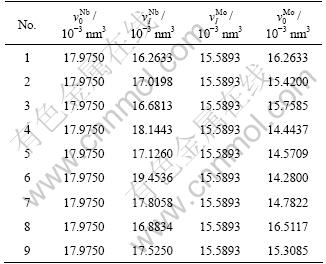
Table 5 Lattice constants of Nb and Mo characteristic crystals of Nb-Mo alloys system by nine interaction equations

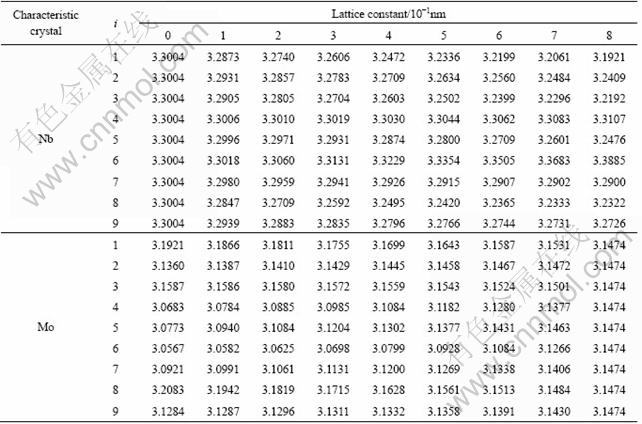
3 Nb and Mo characteristic atom sequences and characteristic crystal sequences of Nb-Mo alloys system in BCC structure

Structural parameters and properties of Nb and Mo characteristic atoms sequences and corresponding characteristic crystals sequences in Nb-Mo alloys system by experimental cohesive energies and lattice constants obtained by the ninth equation are listed in Tables 6 and 7. In the tables, d_c, s_c and p_c are the number of covalent electrons in s，p, and d orbits; e_c is the summation of covalent electrons; e_f is the summation of free electrons; e_n is the summation of non-bonded electrons; R is the single radius; r_i is the bond length of the ith neighbor bond; n_i is the number of the ith neighbor bond; E₁ is the bond energy in the nearest neighbor bond; E_c is cohesive energy.

4 Properties of disordered Nb_(1-x)Mo_x alloys system in BCC structure

The properties of alloys are described by average properties of components. The properties of disordered alloys are obtained by additive law of characteristic crystals. Therefore, electronic structure and properties of disordered Nb_(1-x)Mo_x alloys system as a function of composition x_Mo are listed in Table 8.

The electronic structures and properties of disordered Nb_(1-x)Mo_x alloys system as function of composition x_Mo are shown in Figs. 1-3. As can be seen in Fig. 1, the number of covalent electrons e_c increases and the number of free electron e_f  decreases with the concentration of Mo increasing. This is consistent with the cohesive energy. Figure 2 illustrates the relationship between bond length and composition. Single bond radius reduces with increasing the concentration of Mo. Figure 3 shows the relationship between the nearest neighbor bond length and bond energy. Bond length becomes short with increasing the concentration of Mo, electron pairs increase and bond energy decreases, and the change trend is very similar to that of electronic structure.

Table 6 Structural parameters and properties of Nb characteristic atom sequences and corresponding characteristic crystal sequences in Nb-Mo alloys system

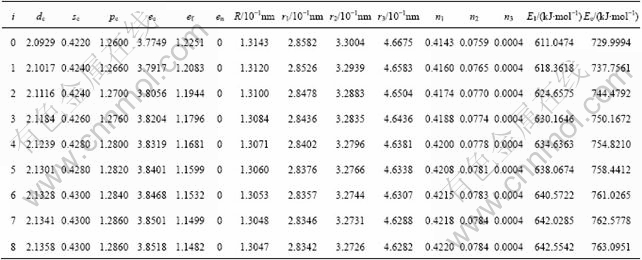
Table 7 Structural parameters and properties of Mo characteristic atom sequences and corresponding characteristic crystal sequences in Nb-Mo alloys system

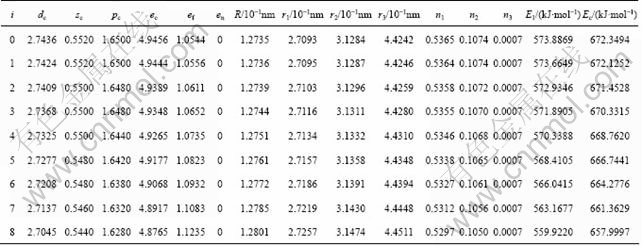
Table 8 Electronic structure and properties of disordered Nb_(1-x)Mo_x alloys system as function of composition x_Mo

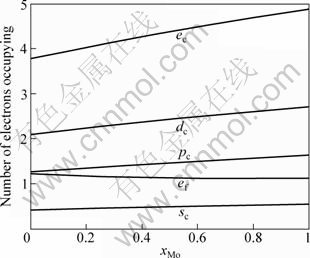
Fig. 1 Electronic structure of disordered Nb_(1-x)Mo_x alloys system as function of composition x_Mo

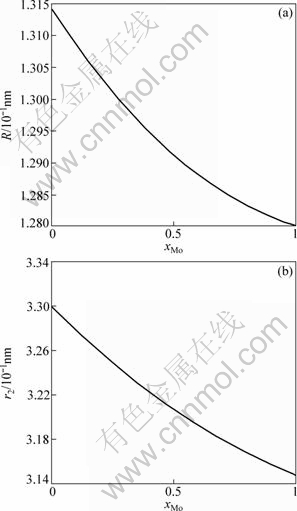
Fig. 2 Single bond radius (a) and lattice constants (b) of disordered Nb_(1-x)Mo_x alloys system as function of composition x_Mo

5 Conclusions

1) On the basis of idea of systematic science of alloys and experimental lattice constants and heats of formation, comprehensively considering the energy, volume and electronic structure of alloys, the ninth equation was determined as the interaction equation of Nb-Mo alloys system.

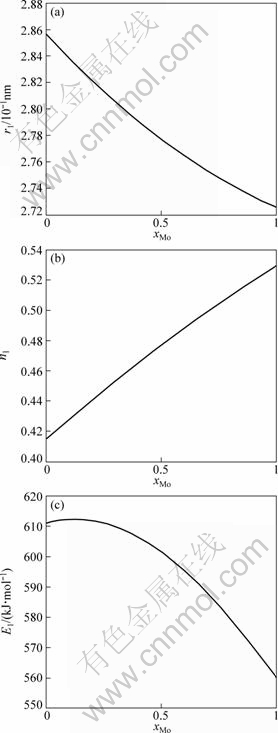
Fig. 3 The nearest neighbor bond length (a), number of electrons (b) and bond energies (c) of disordered Nb_(1-x)Mo_x alloys system as function of composition x_Mo

2) The structural parameters and properties of Nb and Mo characteristic atoms sequences and corresponding characteristic crystals sequences were determined in Nb-Mo alloys system. The electronic structures and physical properties of disordered Nb_(1-x)Mo_x alloys system were calculated according to concentration of characteristic atoms of disordered alloys and basic information of characteristic atom sequences and characteristic crystal sequences.

3) The change trend of physical properties is the same as that of electronic structure.

References

[1] XIE You-qing. Atomic energies and Gibbs energy functions of Ag-Cu alloys [J]. Science in China E, 1998, 41: 146-156.

[2] XIE You-qing, ZHANG Xiao-dong. Atomic volumes and volumes functions of Ag-Cu alloys [J]. Science in China E, 1998, 41: 157-168.

[3] XIE You-qing, ZHANG Xiao-dong. Electronic structure of Ag-Cu alloys [J]. Science in China E, 1998, 41: 225-236.

[4] XIE You-qing, ZHANG Xiao-dong. Phase diagram and thermodynamic properties of Ag-Cu alloys [J]. Science in China E, 1998, 41: 348-356.

[5] XIE You-qing, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang. Volume sequences of characteristic atoms separated from experimental volumes of AuCu and AuCu₃ compounds [J]. Transaction of Nonferrous Metals Society of China, 2009, 19: 1599-1617.

[6] XIE You-qing, LI Yan-fen, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang. Systematic science of Au-Cu system based on experimental data of disordered alloys: Characteristic atom occupation patterns of Au₃Cu, AuCu₃, AuCu I and AuCu II [J]. Transaction of Nonferrous Metals Society of China, 2011, 21: 1092-1104.

[7] XIE You-qing, LI Xiao-bo, LIU Xin-bi, PENG Hong-jian, NIE Yao-zhuang. Volume sequences of characteristic atoms separated from experimental volumes of disordered Au_(1-x)Cu_x alloys [J]. Journal of Materials Science and Engineering, 2009, 3: 54-75.

[8] XIE You-qing, LI Xiao-bo, LIU Xin-bi, PENG Hong-jian, NIE Yao-zhuang. Potential energy sequences of characteristic atoms on basis of heats of formation of disordered Au_(1-x)Cu_x alloys [J]. Journal of Materials Science and Engineering, 2009, 6: 44-57.

[9] XIE You-qing, TAO Hui-jin, PENG Hong-jian, LI Xiao-bo, LIU Xin-bi, PENG Kun. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC TiAl₂ type alloys [J]. Physica B, 2005, 366: 17-37.

[10] XIE You-qing, PENG Hong-jian, LIU Xin-bi, PENG Kun. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC Ti₃Al-type alloys [J]. Physica B, 2005, 362: 1-17.

[11] XIE You-qing, LIU Xin-bi, PENG Kun, PENG Hong-jian. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC TiAl₃-type alloys [J]. Physica B, 2004, 353: 15-33.

[12] XIE You-qing, PENG Kun, LIU Xin-bi. Influences of x_Ti/x_Al on atomic states, lattice constants and potential energy planes of ordered FCC TiAl-type alloys [J]. Physica B, 2004, 344: 5-20.

[13] PENG Hong-jian, WU Qing, LI Xiao-bo, XIE You-qing, Computation of concentration of characteristic atoms of alloys in BCC structure [J]. Science in China E, 2011, 41: 1167-1174.

[14] SINGHAL S C, WORRELL W L. A high-temperature thermodynamic investigation of the Nb-Mo system [J]. Metall Trans, 1973, 4: 1125-1128.

[15] PEARSON W B. A handbook of lattice spacings and structures of metals and alloys [M]. London: Pergmon Press, 1958.

BCC结构Nb-Mo合金系的特征原子序列及无序合金的性质

彭红建^1,2，武 青¹，李小波²，谢佑卿²

1. 中南大学 化学化工学院，长沙 410083；

2. 中南大学 材料科学与工程学院，长沙 410083

摘  要：根据系统合金科学的思想，结合实验晶格常数和生成热，综合考虑合金能量、体积、原子状态之间的相互关系，确定BCC 结构Nb-Mo合金系的相互作用方程为第9方程；同时，确定Nb-Mo合金系中Nb和Mo特征原子序列和特征晶体序列的基本信息；根据无序合金的特征原子浓度计算了无序Nb_(1-x)Mo_x合金的电子结构和物理性质，其物理性质的变化趋势与电子结构的变化极其一致。

关键词：Nb-Mo合金系；特征原子序列；无序合金；性质

(Edited by YANG Hua)

Foundation item: Project (50954006) supported by the National Natural Science Foundation of China; Project (2009GK3152) supported by the Hunan Science and Technology Department, China; Project (201012) supported by the Hunan Provincial Construction Department, China; Project (K1003048-11) supported by the Changsha City Science and Technology Department, China

Corresponding author: PENG Hong-jian; Tel: +86-731-88879287; E-mail: phj108@163.com

DOI: 10.1016/S1003-6326(11)61304-6