J. Cent. South Univ. (2012) 19: 1092-1097
DOI: 10.1007/s11771-012-1114-2
Mathematical models and expert system for
grate-kiln process of iron ore oxide pellet production (Part I):
Mathematical models of grate process
WANG Yi(王祎), FAN Xiao-hui(范晓慧), CHEN Xu-ling(陈许玲)
School of Minerals Processing and Bioengineering, Central South University, Changsha 410083, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: Grate process is an important step in grate-kiln pellet production. However, as a relatively closed system, the process on grate is inaccessible to direct detection, therefore, it is hard to control. As a result, mathematical models of temperature distribution, moisture distribution and oxidation degree distribution in pellet bed, with good universality, computation speed and calculation accuracy, are presented based on analysis of heat transfer and physical-chemical reactions during grate process. And real-time visualization of temperature, moisture and oxidation degree distribution in pellet bed during grate process is realized. Model validation is displayed, and the similarity of 91% is proved. The results can reveal real time status on grate, and provide a solid foundation for the subsequent study of artificial intelligence control system of pellet production.
Key words: mathematical model; temperature distribution; moisture distribution; oxidation degree distribution; iron ore oxide pellet
1 Introduction
Iron ore pellet with high grade, good reducibility, homogeneous particle size, stable composition and favorable physical-chemistry characteristics is a desirable feedstock for ironmaking furnaces. Moreover, it is adapted to the resource conditions in China, as well as the international mineral trade. Therefore, pelletizing gets growing concern and is gradually developed.
Grate-kiln is a widely used process for iron ore oxide pellet production in China. It is treatable, solid fuel usable ore, with large capacity, and has better thermal efficiency by recycling use of hot waste gas [1]. In a typical grate-kiln-cooler pellet induration system, green pellets enter the induration system by charging on grate. They go through grate, kiln and cooler successively, and are finally discharged as finished pellets. Gas is blown into induration system by combustion fan and blower fans of cooler process. It is circulated in grate, kiln and cooler, exchanging heat with pellets, and finally exhausted from gas hood of updraught drying (UDD) section, main exhaust fan, and gas hood of the fourth section of cooler.
Grate-kiln process has been applied to iron ore oxide pellet production for decades. Yet, the level of production control is still low [2-4]. One of the reasons is lack of real-time status information caused by detection difficulties. For this reason, mathematical models have been put forward since 1960s [5-11]. However, applications of these models are basically limited to parameter adjustment during pellet plant design and system evaluation after putting into use, due to hard captured input data and unsatisfied solutions. Another reason obstructing development of control level is that the conventional semi-empirical and semi- instrument production control method is lack of accuracy and normalization. Expert system offers a way out [12]. But, the knowledge acquisition is still difficult due to the complexity caused by circulating air.
Studies were taken out addressing grate-kiln iron ore oxide pellet production control, combining mathematical models and expert system together. The discussion consists of two parts, i.e. mathematical models of grate process and model of kiln temperature field and expert system for pellet production control.
In this work, mathematical models of grate process, including mathematical models of temperature distribution, moisture distribution and oxidation degree distribution in pellet bed are presented. Compared with former studies, this work focused on improving the universality and computation speed of these models,moreover, providing more abundant and more intuitive real time information for production control.
2 Modelling
2.1 Model of temperature distribution in pellet bed
Grate consists of four sections which are updraught drying (UDD), downdraught drying (DDD), tempered preheating (TPH) and preheating (PH). Pellets at atmospheric temperature are charged on grate, and go through each section in turn, heated by hot gas at 200, 200-400, 600-900 and 1 000-1 150 °C, respectively. Heat transfers between pellets and gas flow due to the existence of temperature gradient, pellet temperature increases, and reactions take place, accompanied by enthalpy changes.
For solid phase, pellet bed moves horizontally in grate running direction. In unit time, heat accumulation equals the difference between heat incomings and outgoings. Heat incomings include heat transferred from gas to pellets, heat released by oxidation of magnetite, heat released by water condensation and heat released by other reactions, while heat outcoming refers to heat absorbed by water evaporation. Heat conduction inside pellet bed is neglected.
For gas phase, gas is blown vertically through the pellet bed. Heat transfer in grate running direction is neglected, and heat released and absorbed by reactions is assumed to be exchanged solely with solid phase except water condensation. Therefore, the rate of heat change in gas equals the difference between heat incomings and outgoings. Heat incoming is heat released by water condensation, while heat outcoming is heat lost to pellets, minus the part goes to evaporation.
Therefore, energy balance equations of solid phase and gas phase are
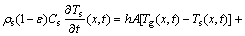
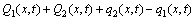 (1)
(1)
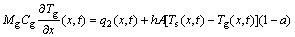 (2)
(2)
where Ts(x, t) and Tg(x, t) are the temperatures of pellets and gas, respectively, which are the target parameters of this model (°C); x is bed depth (cm); t is time (s); A is pellet area for heat transfer (cm2/cm3); ρs is density of ore, which is decided by raw materials (g/cm3); ε is porosity in pellet bed, which is related to shape of pellet and loading condition, and it is a constant in a specific production process; Mg is mass flow of gas, which is obtained by detection value of gas volume (g/cm2·s); α is fraction of heat transfer which goes to evaporation and is related to pellet bed temperature and pellet moisture content. Parameter a is discussed detailedly in model of moisture distribution; Cs is specific heat of pellets, Cg is specific heat of air (J/(g·K)); parameters Cs and Cg are related to pellet bed temperature and gas temperature, respectively; h is heat transfer coefficient between gas and pellets, which is related to gas temperature, gas flow characteristics and pellet diameter (J/(K·s)). Q1(x,t), q1(x,t), q2(x,t) and Q2(x,t) are heat release/absorb rates by oxidation of magnetite, water evaporation, water condensation and other reactions, respectively (J/(s·cm)). The first three rates are discussed detailedly in model of moisture distribution and model of oxidation degree distribution. Q2(x,t) is the rate of the heat released by possible reactions and absorbed heat such as carbonates decomposition, sulfides decomposition and oxidation, according to the specific production process.
2.2 Model of moisture distribution in drying section
Gas flow is blown vertically through pellet bed during grate drying process. When the difference between pellet surface vapor pressure and drying medium vapor pressure is positive, the moisture is removed from pellet surface to gas flow, and internal water spreads to the surface. Otherwise, moisture returns to pellet surface and recondensation occurs.
The change rates of moisture content in gas and pellet bed are proportional to water evaporation rate. Therefore,
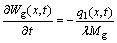 (3)
(3)
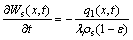 (4)
(4)
where Wg(x,t) and Ws(x,t) are moisture contents in gas and pellet, respectively (%); the initial value of Ws(x,t) is equal to green pellet moisture; λ is latent heat of water evaporation (2 260 J/g).
The formulas for heat transfer rates of water evaporation and condensation are
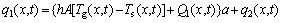 when Ts(x,t)
when Ts(x,t) 100°C (5)
100°C (5)
 when
when  , Tg(x,t)
, Tg(x,t)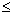 100°C (6)
100°C (6)
where Tg(x,t) and Ts(x,t) are calculated by model of temperature distribution in pellet bed.
Fraction of heat transfer which goes to evaporation is calculated by
 (7)
(7)
where Wc is critical moisture level in pellet (2%).
2.3 Model of oxidation degree distribution in preheating section
Oxidation of magnetite occurs significantly in preheating section during grate-kiln induration process. It is consistent with unreacted shrinking core model [13- 14]. Oxidation degree of magnetite χ is calculated by
 (8)
(8)
where r0 is outside radius of pellet (cm); rm(t) is radius of magnetite unreacted core at t (cm).
According to the unreacted shrinking core theory, the reaction interface moves forward to the pellet core along with oxidation reaction. The moving rate of reaction interface is
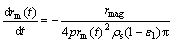 (9)
(9)
where ε1 is porosity in pellets; rmag is reaction rate of magnetite (mol/s), which is defined by the following equation based on kinetics of gas-solid reaction with a solid product layer:
 (10)
(10)
Therefore, the heat release rate of magnetite oxidation can be calculated by formula Q1(x,t)=ΔH1rmag· N1, where c(O2) is concentration of O2 in gas phase (mol/cm3), kg(O2) is mass transfer coefficient of O2 in gas through the gas boundary layer (cm/s); kr is chemical reaction rate of magnetite (cm/s); D(O2) is the diffusivity of O2 in pellet through solid product layer (cm2/s). Parameter kr and D(O2) are temperature dependent parameters, which are calculated by results of Tg and Ts from temperature distribution model; ΔH1 is the enthalpy change of magnetite oxidation (J/mol); N1 is number of pellets per unit volume.
Parameter p is magnetite content in green pellet, (mol/g). It can be calculated with the following equation based on detected data of raw material discharge rates and test results of raw material chemical compositions. Of particular note is that time lag is existent in pellet production, therefore, parameters in this equation is not of the same time.
 (11)
(11)
where mi is the discharge rate of raw material i (t/h); pi is FeO content of raw material i (%); wi is moisture content of raw material i (%). The number, 232, is relative molar mass of magnetite (g/mol); mgreenpellet is output rate of green pellet (t/h); mreturn is output rate of green pellet returning charge (t/h).
3 Model solution
Three grate models above are in differential equation form. Finite-difference method is adopted for model solution [15].
First of all, the solving domain is divided into a number of 0.2 m×wb×(hb/10) size fictitious heat transfer units (wb means the width of pellet bed and hb means the height of pellet bed), as shown in Fig. 1. Each column stands for a heat transfer unit, in which no temperature gradient exists. Hot gas goes in and out during time period Δt, which equals the quotient of unit length and grate running speed. The length of 0.2 m can satisfy the control accuracy without overloaded calculation amount. Pellets and gas distributions are assumed to be even in grate width, therefore, no more division is necessary in width. The height of one tenth of actual bed height is based on the fact that 200 mm is the common design height of pellet bed, and the actual height during production is a little lower, therefore, one tenth of actual bed height approximates to the height of single pellet layer.
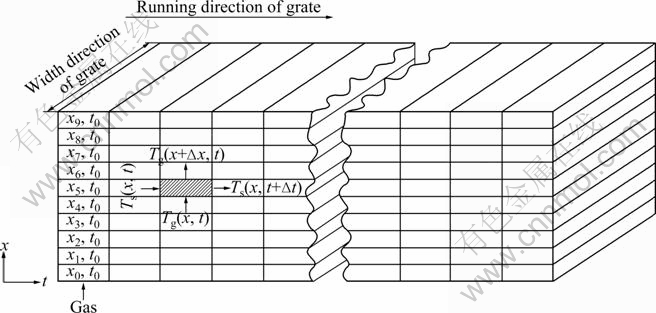
Fig. 1 Grid division
Afterwards, derivative expressions in differential equation are replaced with equivalent difference quotients. The solutions of differential equations are approximated by solving these difference equations.
As shown in Fig. 1, x is the height direction of pellet bed, t represents running direction of grate, and the origin is set at the bottom of the feeding end, i.e. column (x0, t0). Parameter Δx and Δt are obtained by detecting real-time data of bed height and grate running speed. The calculation starts at (x0, t0) which is the intersection of pellet feed entrance and gas entrance. The initial temperature of pellet bed is atmospheric temperature and the initial temperature of gas is detected data of gas in wind boxes of UDD section. Substituting real-time production data into the difference equations gives the values of target parameters, i.e. temperature, moisture content and oxidation degree of pellet bed in this column. Then move to column (x1, t0), and calculate with the same solving process, using the results of previous columns as known conditions. This process goes on until all pellet layers in height direction are calculated at t-coordinate position t0.
Similarly, calculations are taken out along t- coordinate, column by column, until values of temperature, moisture content and oxidation degree of the entire pellet bed are obtained. Of particular note is that the computation sequence is not the same in different sections according to the flow direction of gas. For UDD section, it is from the bottom up. While in DDD, TPH and PH section, it is the opposite.
4 Application and validation
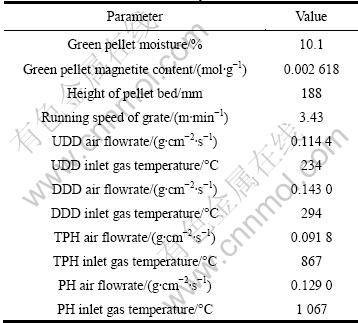
Software was developed with Visual C++. This system was put into field practice in a certain pellet plant in China. A set of production data was collected as listed in Table 1.
Table 1 Production data of auxiliary variables
Pellet bed temperature of each computing unit was calculated by mathematical models above. The results were converted into RGB values by data-image mapping. And two-dimensional distribution of pellet bed temperature was displayed visually on the screen with color code label. As assistance, pellet bed temperature, moisture content and oxidation degree are displayed synchronously in the form of data information when the mouse rests on the temperature field bitmap (see Fig. 2).
Figure 2 shows that the pellet bed temperature in preheating section increases significantly. Hot gas blows vertically through the pellet bed from top to bottom. As a result, the upper layers have higher temperatures than the lower ones. At the discharge point of grate, the top layer is 1 085 °C, while the bottom layer is only 738 °C.
The average values of vertical layers along grate running direction are obtained. And curves of pellet bed temperature, oxidation degree and moisture content are plotted, as shown in Figs. 3-5.
These curves reflect the real-time status on grate. At the discharge point of grate, the average temperature of preheated pellets is 968 °C (see Fig. 3), the average oxidation degree is 85.27% (see Fig. 4), and the moisture in pellet is completely dried out at about 12 m from the feed point (see Fig. 5).

Fig. 2 Two-dimensional visualization of pellet bed temperature distribution on grate

Fig. 3 Change of pellet bed temperature along grate running direction
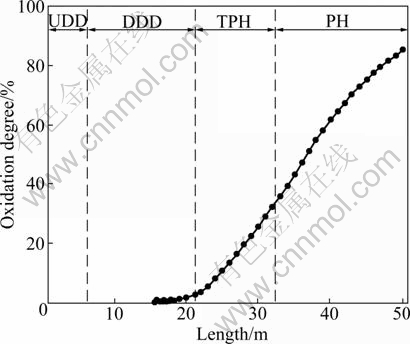
Fig. 4 Change of pellet bed oxidation degree along grate running direction
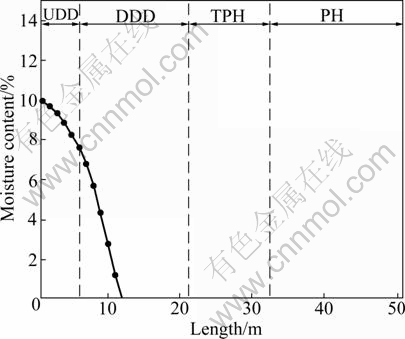
Fig. 5 Change of pellet bed moisture content along grate running direction
The outlet gas temperatures of each zone are detected by thermocouples fixing into some gas hoods and wind boxes. These detected data can be used as a comparison of the calculated results for model validation. The comparison is shown in Fig. 6.
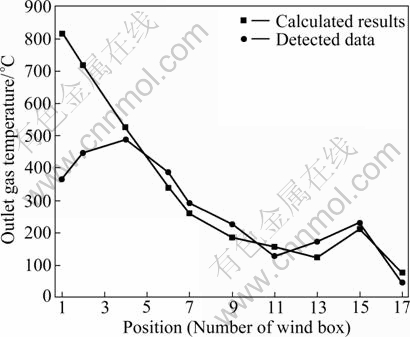
Fig. 6 Comparison of calculated outlet gas temperatures with detected values on production field
The results in Fig. 6 indicate that calculated values of outlet gas temperature show great consistency with the detected values, except in the corresponding position of No. 1 and No. 2 wind box. And the reason of this exception is air leak. Outlet gas of PH section is pumped into gas hood of DDD section by regenerative fans. Therefore, gas pressure in wind boxes of PH section is negative. Air at atmospheric temperature leaks into these wind boxes due to seal defects of the equipment. And obviously, the wind boxes near the end of grate have greater impact, which leads to the deviation of detected values.
The 200 sets of production data under steady state were collected for further validation. The results show that when the threshold is 0.1, variation trends of calculated outlet gas temperatures and detected values have a similarity of 91%.
5 Conclusions
1) Mathematical models of temperature distribution, moisture distribution and oxidation degree distribution in pellet bed are developed by analysis of heat transfer and physical-chemical reactions during grate process.
2) To achieve a speed fast enough for on-line calculation, finite-difference method is adopted for model solution based on a number of 0.2 m×wb×(hb/10) size fictitious heat transfer units.
3) Software is developed with Visual C++, and real-time status in pellet bed during grate process is obtained by model calculation with production data. The results are validated with detected data of outlet gas temperature, and great consistency is proved.
4) Mathematical models of grate process can make up deficiencies of the existing detection techniques and meet the requirement of online operation. The results provide us with easy access to a wealth of real-time production information and contribute to making correct control guidance, and stabilizing pellet production consequently.
References
[1] FU Ju-ying, JIANG Tao, ZHU De-qing. Sintering and pelletizing [M]. Changsha: Central South University Press, 1995: 310-311. (in Chinese)
[2] ZHANG Yong, WANG Jie-sheng, WANG Wei. Design and application of integrated automation system for pelletizing plant [C]// Proceedings of the 6th World Congress on Intelligent Control and Automation. Dalian, 2006: 6719-6723.
[3] de ALMEIDA RIBEIRO P R, de ALMEIDA NETO A, de OLIVEIRA A C M. Multi-Network-Feedback- Error-Learning in pelletizing plant control [C]// Proceedings of the 2nd IEEE International Conference on Advanced Computer Control. Shenyang, 2010: 340-344.
[4] LIU Bin, LI Hong-ru, YANG Ji-fan. Forecast for the thermal state index of pellet mine based on artificial neural network [C]// Proceedings of the 2011 Chinese Control and Decision Conference. Mianyang, 2011: 3068-3072.
[5] YOUNG R W, CROSS M, GIBSON R D. Mathematical model of grate-kiln-cooler process used for induration of iron ore pellets [J]. Ironmaking and Steelmaking, 1979, 6(1): 1-13.
[6] THURLBY J A. A dynamic mathematical model of the complete grate/kiln iron-ore pellet induration process [J]. Metallurgical Transaction B, 1988, 19B(1): 103-112.
[7] TSUKERMAN T, DUCHESNE C, HODOUIN D. On the drying rates of individual iron oxide pellets [J]. International Journal of Mineral Processing, 2007, 83(3/4): 99-115.
[8] BARATI M. Dynamic simulation of pellet induration process in straight-grate system [J]. International Journal of Mineral Processing, 2008, 89(1/4): 30-39.
[9] SADRNEZHAAD S K, FERDOWSI A, PAYAB H. Mathematical model for a straight grate iron ore pellet induration process of industrial scale [J]. Computational Materials Science, 2008, 44(2): 296-302.
[10] LIANG Ru-quan, HE Ji-cheng. Moving behavior of pellets in a pellet shaft furnace [J]. Journal of Central South University of Technology, 2008, 15(1): 280-283.
[11] MAJURNDER S, NATEKAR P V, RUNKANA V. Virtual indurator: A tool for simulation of induration of wet iron ore pellets on a moving grate [J]. Computers and Chemical Engineering, 2009, 33(6): 1141-1152.
[12] Petrica Vizureanu. Expert systems [M]. Vukovar: Intech, 2010: 65-90.
[13] PAPANASTASSIOU D, BITSIANES G. Mechanisms and kinetics underlying the oxidation of magnetite in the induration of iron ore pellets [J]. Metallurgical Transactions, 1973, 4(2): 487-496.
[14] FORSMO S P E, FORSMO S E, SAMSKOG P O, BJORKMAN B M T. Mechanisms in oxidation and sintering of magnetite iron ore green pellets [J]. Powder Technology, 2008, 183(2): 247-259.
[15] Croft D R, Lilley D G. Calculation of finite difference equation of heat transfer [M]. ZHANG Feng-lu, Tr. Beijing: Metallurgical Industry Press, 1982: 113-135. (in Chinese)
(Edited by DENG Lü-xiang)
Foundation item: Project(NCET050630) supported by Program for New Century Excellent Talents in University, China
Received date: 2011-05-24; Accepted date: 2011-09-23
Corresponding author: FAN Xiao-hui, Professor; Tel: +86-731-88877952; E-mail: csufanxiaohui@126.com