Trans. Nonferrous Met. Soc. China 23(2013) 2329-2335

Thermo-electric behaviour of NiTi shape memory alloy

H. N. BHARGAW¹, M. AHMED¹, P. SINHA²

1. CSIR-Advanced Materials and Processes Research Institute, Bhopal, Madhya Pradesh – 462064, India;

2. Department of Electronics, Institute of Engineering & Technology, Barkatullah University, Bhopal, Madhya Pradesh – 462026, India

Received 6 September 2012; accepted 26 December 2012

Abstract: The thermo-electric behavior of shape memory alloy (SMA) wire was presented. When the wire was electrically heated above its transformation temperature by current, a large mechanical force is exerted due to transformation in its phases. In order to make use of SMA wire as an actuator, different parameters and their relationships were investigated. These parameters are recoverable strain (displacement), temperature hysteresis and electrical resistance variation under different stress levels. Optimum safe heating current was assessed and phase transformation temperatures were estimated by heat transfer model. The wire was heated and cooled by 680 mA of current for 796 s under natural air convection. The strain recovered is 4.33% and corresponding change in resistance is 11.2% at 43 MPa of stress. The resistance variation shows linearly with displacement and current during heating and cooling cycle respectively. This study will be useful in precisely controlling of SMA wire actuator with and without external sensor feedback.

Key words: shape memory alloy; electrical resistance; phase transformation; hysteresis

1 Introduction

Shape memory alloys (SMAs) are family of smart materials. They have the ability to change their shape depending on their transformation temperatures. SMA, in particular nickel–titanium alloy (Nitinol), is a metallic alloy that exhibits shape memory effect. When it deforms at low temperatures, it has the ability to return to its predetermined shape, if heated above its transformation temperature [1]. The returning to its predetermined shape is the result of crystalline structure transformation from low temperature martensite (M) phase to high temperature austenite (A) phase. These two phases have same chemical compositions except dissimilarity in crystallographic structures. Hence, they show dissimilarities in their thermal, mechanical and electrical properties [2]. The high-temperature austenitic phase is more rigid and stronger as compared with low- temperature martensite phase. The low-temperature phase is also known as twinned martensite phase where each layer is separated by a twinning boundary. This state is highly malleable and has very low elastic limit. When external stress is applied at this state, the material changes into detwinned variant of martensite phase that stores generated strain. The strain can be recovered by heating the material at higher temperatures. During strain recovery, the alloy contracts and exhibits large force against external resistance. It finally transforms into austenite phase [2,3]. A typical schematic diagram of SMA thermal hysteresis is shown Fig. 1. The thermal hysteresis represents material transformation characteristic, which provides four distinct transformation temperatures. M_s and M_f represent the start and finish temperatures of martensite, while A_s and A_f are the start and finish temperatures of austenite, respectively [4-8]. Figure 2 illustrates the SMA wire that is used as an actuator to lift the load. It changes its status with heating current. The shape change in the material is observed by its elastic and plastic deformation as well as thermal expansion and contraction. Moreover, it also exhibits three different types of shape memory effects: one way shape memory effect, two way shape memory effect and pseudoelasticity.

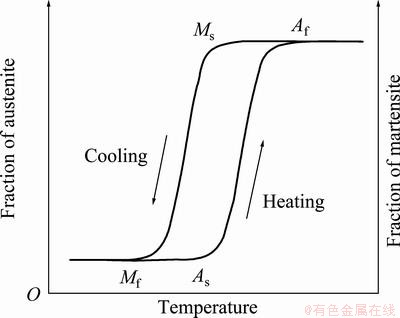
Fig. 1 Schematic diagram of SMA thermal hysteresis

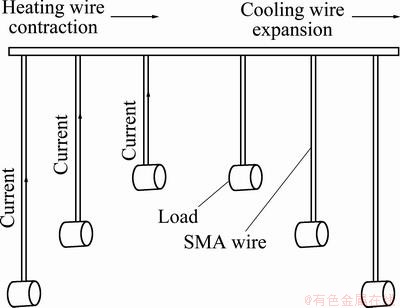
Fig. 2 Shape memory alloy wire actuator

The SMA material can be used for variety of applications as an actuator due to its large strain recovery, high stiffness and strength. A SMA wire of 0.508 mm in diameter can lift as much as 16 pounds with associated strain recovery of 5% [2]. Most of actuator applications use SMA material in form of wire because it is easy to cut and connect, and can be conveniently activated by Joule heating. It offers many advantages like compact size, long actuation life within sustainable strain and stress limits, silent and spark free operation over competing technologies. It is lightweight with high power to mass ratio and high energy density in the order of 10⁷ J/m³ [9]. It also has excellent biocompatibility and corrosion resistance. However, it also has certain limitations such as low power efficiency, low operating frequency, control difficulties due to hysteresis, nonlinearities, parameter uncertainties and un-modeled dynamics [3,10].

The application of SMA wire as an actuator is only possible if the characterizations under various operating conditions are known. The present study emphasizes on thermo-electric characterization of NiTi SMA wire that can be useful in designing a precisely controlled actuator. Different parameters like recoverable strain (displacement), temperature hysteresis and electrical resistance variation under different stress levels and their relationships were investigated.

2 Experimental

2.1 Experimental set-up

For any new application of SMA wire, it should be characterized in order to assess its behavior under loading and stress-free conditions [11]. The important information that comes out during characterization process is electrical resistance (ER) variation and phase transformation temperatures (PTT). The schematic block diagram of experimental setup to characterize the SMA wire is shown in Fig. 3. The block diagram consists of PC with data acquisition system, SMA test bench set-up, voltage controlled current amplifier and power supply. The test bench set-up is assembled by fixing rigid support one side and pulleys mounted on other side to provide frictionless movement to SMA wire during their contraction and expansion. The wire contraction and expansion are measured by the LVDT (linear variable displacement transducer) displacement sensor, which is placed parallel to SMA wire. The SMA wire is bought from Dynalloy Inc. It is sold under the brand name of ‘Flexinol LT’, whose transformation temperature is 70 °C [12]. The test wire diameter is 0.381 mm and the length is 180 mm. One end of the wire is tightly fixed on rigid support. The other free end of the wire and core of LVDT are mounted on common non-metallic strip. The strip is used to avoid any electrical conductivity between them. Dead weight is attached to strip by a thread through pulleys to ensure uni-axial tensile stress generated on the wire. Heating pulse/signal (low voltage ramp signal) is generated in LabVIEW program. The voltage controlled current amplifier is developed to amplify the heating pulse applied to the wire. The input signal during heating and cooling cycle is applied for 796 s at the rate of 1.76 mA/s. The rate and duration of the signal is optimum (explained in section 2.3) for generating enough heat in the wire to achieve requires phase transformation temperatures without damaging the wire. The parameters acquired by data acquisition hardware (USB-6009) under LabVIEW platform are current flow through wire, voltage across wire, displacement and surface temperature of wire.

Fig. 3 Schematic block diagram of experimental set-up

The Joule-heating of the wire and its subsequent contraction and expansion are produced by current (I) that flows through the wire. The current is continuously monitored by measuring voltage drop across 1 Ω ceramic resistance connected in series with the wire. Subsequently, wire electrical resistance (R_e) and electrical power (P) are calculated. Dead weights of different denominations are used to apply constant stress of different levels. The load capacity of the wire depends on their diameter and it is inversely proportional to the speed and time of actuation. For larger diameter of wire, load capacity and energy needed to activate the wire are increased. However, activation time becomes longer, thus the bandwidth decreases [12]. Although, a temperature sensor is also incorporated in the experimental set-up but the accurate temperature measurement is not possible due to small wire dimensions and uncontrolled ambient conditions. Hence, phase transformation temperature is computed using the heat transfer model. The tentative temperature of the wire is experimentally measured and evaluated with computed/simulated temperature by heat transfer model.

2.2 Heat transfer model of transformation temperature

Since the measurement of wire temperature is practically difficult because of its small dimensions and ambient conditions, a heat transfer analysis of wire has been carried out by lumped parameter convective heat transfer equation. The convection heat transfer model determines the rate of heating and cooling due to ramp electric current passing in the wire. The simplified one-dimensional heat transfer expression [6,13,14] that describes the SMA wire for resistive heating and cooling under ambient air convection is defined as

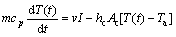                 (1)

where m=ρπd²l/4 is the mass of the wire; ρ, d and l are the density, diameter and length of wire; c_p is the specific heat capacity; h_c is the heat convection coefficient for ambient cooling conditions; T_a is ambient temperature; I is the current flow in the wire; v is the potential difference across the wire; A_c=ρdl is convective surface area of the wire.

The above heat transfer expression assumes that the effect is one dimensional, the load applied to the wire is constant, radiation effects are negligible compared with conduction mode of heat transfer, volume and area changes are negligible, T_a and h_c are constant. It is also assumed that the wire temperature field is spatially uniform and phase transformation temperatures are also considered constants. The effect of heat radiation is neglected as the working temperature is below 200 °C [9]. Equation (1) can be rewritten for heating and cooling process (Eq. 2) and solved for the maximum temperature T of the SMA wire.

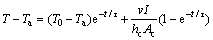           (2)

where T₀ is initial temperature of the wire, and τ (time constant) =mc_p/(h_cA_c). The change of temperature through electrical power during heating and cooling cycle is obtained by considering initial temperature which is equal to the ambient temperature. Thus, Eq. (2) becomes

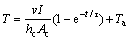                        (3)

The temperature of the wire is controlled indirectly by varying the intensity of current flowing through it. The corresponding shape change starts in the wire when the temperature crosses A_s (austenite start temperature) and ends at A_f (austenite finish temperature). In order to maintain the wire at the austenitic phase, the temperature has to be maintained just above A_f by applying optimal electrical power. SMA wire temperature is computed from Eq. (3). The parameters that are considered for computation measured are current and voltage, wire diameter (381 μm), length (180 mm), c_p (322.384 J/(kg·°C)) and h_c (75 W/(m²·°C)) [15,16]. Figures 4(a) and (b) show the SMA current and voltage signals. Figures 4(c) and (d) show computed temperature profile and thermal hysteresis loop of displacement—temperature relationship.

2.3 Optimization of current intensity

Optimum current required to generate transformation temperature is important to harness the maximum benefit. It is assessed by testing SMA sample at two different peak currents (700 mA and 1000 mA) subjected to two different loads (8.6 and 25.80 MPa). This optimization process is also helpful in order to find out threshold current range above which SMA wire gets overheated. Further, it also provides the value of the threshold current below which it underperforms. Figure 5(a) shows the displacement curves of SMA wire at 1000 mA and 700 mA of currents at stresses of 8.6 and 25.8 MPa, respectively. The corresponding current pulses are reported in Fig. 5(b). In both the cases, pulse heating and cooling rates are different because pulse duration is kept constant in the present investigation. The displacement curves of 1000 mA current starts early with very fast rate of displacement and this rate decreases at higher current due to recovery of maximum strain. Similarly, for displacement curve of 700 mA, displacement in wire starts later with slightly lesser rates but represent larger linear range as compared to 1000 mA displacement curve. The optimum current intensity is obtained from the corresponding current pulses by drawing the perpendicular from the displacement curves. The meeting cross over points on the current pulses (refer Fig. 5(b)) represents the optimum transformation current. The optimum currents are 740 mA and 600 mA for the current pulse of 1000 mA and 700 mA, respectively. Thus, 600 mA of current intensity is sufficient to perform phase transformation in the wire. The threshold current should be considered slightly higher due to environmental conditions and wire transformation temperature need to maintain above its transformation temperature. Therefore, SMA wire characterization is carried out at 700 mA peak current and it is considered a safe heating current for characterization process based on above observation.

Fig. 4 Current (a) and voltage (b) signals with time, computed temperature profile (c) and hysteresis between displacement and temperature (d)

Fig. 5 SMA wire displacement by current pulse of 1000 mA and 700 mA

3 Results and discussion

The relationship between displacement and current intensity of different stress levels is shown in Fig. 6. The wire is heated by increasing current at the rate of 1.76 mA/s. As the current increases, initially small change in length and slope is observed. As the current progresses to attain transformation temperature, a large change in length with higher slope is observed. The wire is fully transformed into austenitic phase and recovers stored stain. During recovery of strain, applied load is lifted with force by the wire. In the cooling cycle, current decreases at the same rate under natural air convection. The wire expands to attain its original length and returns to martensite phase to complete the cycle. Thus, the wire contraction and expansion form the hysteresis loop as shown in Fig. 6. The hysteresis curve is used to find the critical values of the transformation currents on which transformation temperature depends. The experiments are carried out at different stress levels to investigate its behavior. It is clearly observed that the hysteresis curve shifts towards right with increase in stress level and corresponding decrease of hysteresis width. The required heating current also increases with increase in stress. Thus, the wire temperature is a function of applied current and shift of hysteresis curve towards higher current represents the increase in phase transformation temperature. Therefore, the applied current is a function of applied stress. The reduction of hysteresis width is mainly due to shift in cooling cycle curves. The shift is mainly due to formation of different variants of martensite phase at different stresses.

Fig. 6 Displacement—current hysteresis at different stresses

The thermo-electric behavior of SMA wire is characterized at 43 MPa. Figure 7 shows the wire parameters of voltage, current and displacement due to their expansion and contraction during heating and cooling cycle. The wire expansion and contraction are induced both mechanically and thermally. The displacement curve shows that wire is contracted by 7.8 mm (4.33%) from initial length of 180 mm. In the displacement curve, contraction is performed with larger slope during heating cycle. During cooling cycle, wire expansion rate is low at the beginning and as the time passes, expansion rate increases very fast. In the voltage curve, flat region is observed on top during contraction/heating cycle as current increases linearly. The flat region is due to start of austenite phase from detwined martensite phase. In this region, a large contraction in wire length (3.5%) is observed by slight increase in heating current (~100 mA). In this region, material absorbs the highest electrical energy for reorientation of internal phase structure. It also causes to change in dimensions and resistivity, which is based on different states of material during transformations. The voltage curve shows variation in slope during expansion/cooling cycles due to formation of different variants of martensite phases.

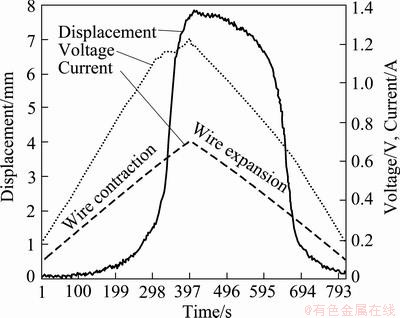
Fig. 7 Current, voltage and displacement curve during heating and cooling cycle

The electrical resistance computed by the measured SMA voltage and current is shown in Fig. 8. At the beginning, wire resistance increases as the electrical power increases and then starts decreasing when the wire temperature reaches the austenitic start (A_s) temperature. The resistance decreases at higher rates until the SMA wire is fully transformed to austenitic phase. At this stage, wire shows the lowest resistance in heating cycle due to large reorientation in crystallographic structure. The resistance variation is mainly due to the fact that the resistivities of Nitinol in martensite and austenitic phases are different (100 and 80 μΩ·cm, respectively). The actual resistance of the wire in each moment is given by the amount of each phase present in that state (phase), temperature dependent value of the resistivity of each phase and the exact dimension of the wire (length and cross section area). It is clear that the complicated relationship between the wire dimensions and its resistance exists. The relationship is simpler for different resistances in the heating and cooling cycle established. In the cooling cycle, wire resistance increases at slower rates as compared with heating cycle, whereas voltage and current are decreased. So, the resistance variation curve follows different trends from martensite to austenite phase and vice versa. The experimental results show that the wire resistance drops by 11.2% and recovers back at the end of the cycle.

Fig. 8 Resistance variation during heating and cooling cycle

The relationship between applied current and resistance during heating and cooling cycle is shown in Fig. 9. The resistance behavior is non-linear and it displays hysteresis during phase transformation. Its variation is non-monotonic as it shows parabolic-like shape during heating and quite linear trend in cooling cycle. It initially increases with small slope as the current increases and then decreases linearly by sharp negative slope. Similarly, the wire resistance increases in cooling cycle with higher slope as the current decreases and then decreases to attain its initial value. The hysteresis curve varies between 300 mA and 700 mA of current. The cooling cycle is co-insides with heating curve below 300 mA but the direction is opposite. In the hysteresis, resistance partly maintains linearity during heating and cooling cycle with different slopes at different currents.

The resistance and displacement are internal properties of material which depend on material compositions, transformation temperatures and applied stress. The relationship between resistance and displacement forms hysteresis shown in Fig. 10. In the hysteresis, resistance corresponding to the same displacement is different in the heating and cooling cycle. Similarly, the slope of the curves is also different during heating and cooling. As shown at the bottom of the hysteresis curve, the resistance increases without changes in the displacement with increase in wire temperature. It shows zero slope before the transformation starts and the material behaves like metal. As the wire temperature gradually increases to attain transformation temperature, internal structure of the material transforms to another crystallographic structure that causes change (contraction) in wire length and correspondingly wire resistance. The decrease of wire resistance during transformation is linear function of displacement with negative slope. In contrast, wire resistance varies differently during cooling cycle with the same change in wire length (expansion). During cooling cycle, resistance curve follows parabolic- like path. The main reason of the hysteresis in the relationship is different intermediate phase formation during cooling. The material directly transforms to austenitic phase from detwined martensite phase during heating cycle but in cooling cycle, it first transforms to R-phase and then martensite phase. R-phase has similar crystallographic structure to martensite phase with smaller resistance. It can be concluded that the resistance varies linearly with current and displacement during cooling and heating cycle respectively as shown in Figs. 9 and 10.

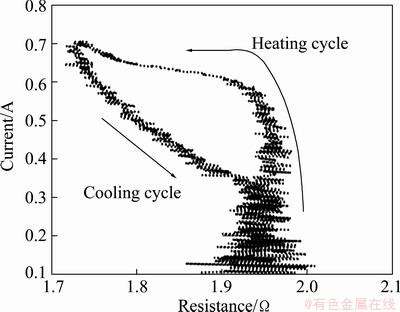
Fig. 9 Relationship between applied current and resistance

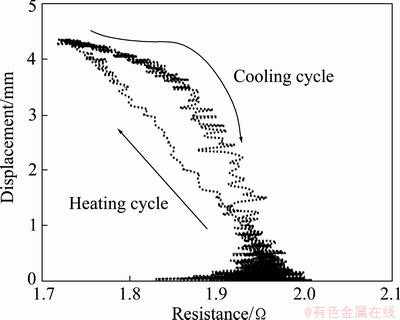
Fig. 10 Relationship between displacement and resistance

4 Conclusions

The thermo-electric behavior of commercially available SMA wire was presented under different applied stresses. The phase transformation temperatures are induced by constant rate of Joule (electrical) heating. Therefore, safe limit of heating current is identified. The heat transfer model is used to simulate the phase transformation temperature through heating current and voltage across SMA wire. The actual SMA resistance is measured for each phase present in the wire during transformation. A variation of 11.2% in resistance is observed during transformation from detwined martensite to austenite phase and vice versa. The decreasing rate of resistance is very high in heating cycle as compared with increasing rate of resistance in cooling cycle. The wire resistance exhibits linear function with displacement (contraction) during heating cycle. It also maintains linearity with applied current during cooling cycle. This significant resistance variation plays an important role in controlling SMA actuator without any external sensor feedback. Increase in the stress on wire results in increase of transformation current to recover the generated strain. It also increases corresponding phase transformation temperature of the wire. Therefore, it is important to perform an electro-thermo-mechanical characteristic of the wire for designing an exact application of SMA wire.

Acknowledgements

The authors would like to acknowledge the Director, Advanced Materials and Processes Research Institute and Dr. Rupa Dasgupta who have supported at various stages of this reported work.

References

[1] MA N, SONG G. Control of shape memory alloy actuator using pulse width modulation [J]. Smart Mater Struct, 2003, 12(5): 712-719.

[2] MA N, SONG G, LEE H J. Position control of shape memory alloy actuators with internal electrical resistance feedback using neural networks [J]. Smart Mater Struct, 2004, 13(4): 777–783.

[3] DUTTA S M, GHORBEL F H. Differential hysteresis modeling of a shape memory alloy wire actuator [J]. IEEE Transactions on Mechatronics, 2005, 10(2): 189-197.

[4] OTSUKA K, WAYMAN C M. Shape memory materials [M]. Cambridge: Cambridge University Press, 1998.

[5] FUNAKUBO H. Shape memory alloys [M]. Glasgow, UK: Bell and Bain Ltd, 1984.

[6] DONALD J L. Engineering analysis of smart material systems [M]. Hoboken, New Jersay: John Wiley & Sons, Inc, 2007.

[7] LAGOUDAS D C. Shape memory alloys: Modeling and engineering applications [M]. NY, UAS: Springer, 2008.

[8] HASSAN S, DIRK S. Mathematical models of shape memory alloy behavior for online and fast prediction of the hysteretic behaviour [J]. Nonlinear Dyn, 2010, 62: 53-66.

[9] KHOL M. Shape memory micro actuators [M]. Berlin, Heidelberg: Springer-Verlag, 2004.

[10] MING H W, SCHETKY L M. Industrial applications for shape memory alloys [C]//Proceedings of the International Conference on Shape Memory and Superelastic Technologies. California, 2000: 171-182.

[11] NESPOLI A, BESSEGHINI S. A complete thermo-mechanical study of a NiTiCu shape memory alloy wire [J]. Journal of Therm Anal Calorim, 2010. DOI 10.1007/S 10973-010-1042-Z

[12] Technical data sheet of Dynalloy SMA wire [EB/OL]// http://www.dynalloy.com/pdfs/TCF1140.pdf.

[13] MEIER H, OELSCHLAEGER L. Numerical thermomechanical modelling of shape memory alloy wires [J]. Material Science and Engineering A, 2004, 378: 484-489.

[14] BRAILOVSKI V, TROCHU F, DAIGNEAULT G. Temporal characteristics of shape memory linear actuators and their application to circuit breakers [J]. Materials and Design, 1996, 17(3): 151-158.

[15] MADILL D R, WONG D. Modeling and L2-stability of a shape memory alloy position control system [J]. IEEE Transactions on Control Systems Technology, 1998, 6(4): 473-482.

[16] SHU S G, LAGOUDAS D C, HUGHES D, WEN J T. Modeling of flexible beam actuated by shape memory alloy wires [J]. Smart Material Structure, 1997, 6: 265-277.

NiTi形状记忆合金的热电行为

H. N. BHARGAW¹, M. AHMED¹, P. SINHA²

1. CSIR-Advanced Materials and Processes Research Institute, Bhopal, Madhya Pradesh – 462064, India;

2. Department of Electronics, Institute of Engineering & Technology, Barkatullah University, Bhopal, India

摘  要：研究了形状记忆合金线的热电行为。当合金线被加热到温度高于其相变温度时，由于相的转变而产生一个大的机械力。将SMA线用作驱动器，并研究了不同的参数及它们之间的关系。在不同的压力水平下，这些变化的参数分别是弹性应变(位移)、温度磁滞和电阻。通过传递热模型得到安全的加热电流并预测了相变温度。在自然空气对流的条件下，采用680 mA的电流加热、冷却合金线796 s。在43 MPa的应力水平下，应变恢复率为4.33%，相应的电阻变化为11.2%。在加热、冷却循环过程中，电阻变化与位移和电流分别呈线性关系。该研究有助于精确控制有、无外部传感器反馈的SMA线驱动器。

关键词：形状记忆合金；电阻；相变；磁滞

(Edited by Xiang-qun LI)

Corresponding author: H. N. BHARGAW; Tel: +91-755-2457244-1117; Fax: +91-755-2457042; E-mail: bhargawhnb1@gmail.com

DOI: 10.1016/S1003-6326(13)62737-5