Immune response-based algorithm for optimization of dynamic environments
来源期刊:中南大学学报(英文版)2011年第5期
论文作者:史旭华 钱锋
文章页码:1563 - 1571
Key words:dynamic optimization; artificial immune algorithms; immune response; multi-scale variation
Abstract:
A novel immune algorithm suitable for dynamic environments (AIDE) was proposed based on a biological immune response principle. The dynamic process of artificial immune response with operators such as immune cloning, multi-scale variation and gradient-based diversity was modeled. Because the immune cloning operator was derived from a stimulation and suppression effect between antibodies and antigens, a sigmoid model that can clearly describe clonal proliferation was proposed. In addition, with the introduction of multiple populations and multi-scale variation, the algorithm can well maintain the population diversity during the dynamic searching process. Unlike traditional artificial immune algorithms, which require randomly generated cells added to the current population to explore its fitness landscape, AIDE uses a gradient-based diversity operator to speed up the optimization in the dynamic environments. Several reported algorithms were compared with AIDE by using Moving Peaks Benchmarks. Preliminary experiments show that AIDE can maintain high population diversity during the search process, simultaneously can speed up the optimization. Thus, AIDE is useful for the optimization of dynamic environments.
. Cent. South Univ. Technol. (2011) 18: 1563-1571
DOI: 10.1007/s11771-011-0873-5![]()
SHI Xu-hua(史旭华)1, 2, QIAN Feng(钱锋)1
1. Key Laboratory of Advanced Control and Optimization for Chemical Processes, Ministry of Education,
East China University of Science and Technology, Shanghai 200237, China;
2. College of Information Science and Engineering, Ningbo University, Ningbo 315211, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: A novel immune algorithm suitable for dynamic environments (AIDE) was proposed based on a biological immune response principle. The dynamic process of artificial immune response with operators such as immune cloning, multi-scale variation and gradient-based diversity was modeled. Because the immune cloning operator was derived from a stimulation and suppression effect between antibodies and antigens, a sigmoid model that can clearly describe clonal proliferation was proposed. In addition, with the introduction of multiple populations and multi-scale variation, the algorithm can well maintain the population diversity during the dynamic searching process. Unlike traditional artificial immune algorithms, which require randomly generated cells added to the current population to explore its fitness landscape, AIDE uses a gradient-based diversity operator to speed up the optimization in the dynamic environments. Several reported algorithms were compared with AIDE by using Moving Peaks Benchmarks. Preliminary experiments show that AIDE can maintain high population diversity during the search process, simultaneously can speed up the optimization. Thus, AIDE is useful for the optimization of dynamic environments.
Key words: dynamic optimization; artificial immune algorithms; immune response; multi-scale variation
1 Introduction
Dynamic environment optimization problems (DEOs), where the global solution moves in the search space, arise frequently in the engineering applications. Generally, DEOs can be defined as
![]() (1)
(1)
where c(t) is a bounded and closed domain in Rp(t) and f(x, t) denotes a time-varying objective function. For fixed time t, x*![]() c(t) is the optimal solution to the problem above if and only if
c(t) is the optimal solution to the problem above if and only if
![]() (2)
(2)
The search for x* can be considered as the maximization of DEOs. However, reversing the sign in Eq.(1) makes the search for x* a minimization task. In contrast to a static optimization case, the main goal in dynamic problems is not only to detect the environmental changes automatically, but also to respond to the environmental changes so that the moving optimum can be tracked as closely as possible [1-3]. Many algorithms that work efficiently in static problems fail when applied to dynamic problems due to their inability to adapt and respond to changes in the environment. Therefore, studies on static environments are usually insufficient to reveal the performance of an algorithm when the problem is dynamic. This poses a great challenge to traditional methods. To address this challenge, several approaches have been developed in evolutionary algorithms (EAs) to improve their performance in dynamic environments [4-6]. A comprehensive survey can be found in Ref.[7]. These methods, developed by extending existing EAs with major modifications in the operators, allow prompt reaction to time-dependent environments, but they fail in one important area, i.e., how to find the location of the optimum rapidly.
In recent years, artificial immune algorithms (AIAs) have created great interest, due to their great superiority over several classical intelligent techniques such as peculiar immune response, antibody diversity and immune memory, and they have been applied to DEOs as well. However, how to design novel immune algorithms to track dynamically time-varying environments and thereby rapidly discover the optimum of the current environment is still an entirely new research topic. Therefore, in this work, an artificial immune response algorithm suitable for DEOs (AIDE) is proposed based on some characteristics of germinal centers (GCs) of a biological immune system. The algorithm includes several vital schemes: immune cloning, multi-scale variation and gradient-based diversity.
2 Artificial immune algorithms in DEOs
As a kind of robust optimization technique, AIAs have been widely used for stationary optimization problems where the fitness landscape does not change during the course of the computation. Recently, the application of AIAs has been extended to time-varying systems. Theoretically, a biological immune system serves well as a computational metaphor for tackling DEOs due to its ability to maintain and boost diversity [8]. But, when they are actually applied, AIAs face a big challenge, that is, lack of fixed clonal selection implementation and additional evaluations of AIAs, which usually leads to long running time and poor tracking during the search process.
The simple artificial immune system (SAIS) [9] was one of the first attempts to exploit immunity as a metaphor for tackling dynamic optimization. SAIS comprises clonal selection, cell decay, recruitment and idiotypic effects. Although k-tournament selection rather than a local selection schema is adopted, the size of the repertoire is not fixed; therefore, additional evaluations need to be performed. WALKER and GARRETT [10] compared a clonal selection algorithm with an evolutionary strategy and found that the former is superior to the latter when dealing with low-dimension DEOs, but with high-dimension DEOs, the latter optimizes more quickly and at a higher level. PAISA [11] is a population-based architecture with an arti?cial immune dynamic algorithm. Its quaternion (G, I, R, Al) idea, i.e. antigen G, antibody space I, set of reaction rules R and dynamic algorithm Al modeled the dynamic process of human immune response. Opt-aiNet is a multimodal function optimization algorithm that exhibits dynamic allocation of repertoire size [12]. It comprises affinity maturation, recruitment of new random cells and idiotypic effects that cause similar cells to be removed. A modified version, called Dopt-aiNet, which deals with dynamic environments, is described in Ref.[13]. It extends Opt-aiNet to a separate memory population, a search procedure for controlling decay, new mutation operators and a different measure of affinity. These additions can improve Opt-aiNet’s ability to find the optimal solutions quickly and maintain the diversity when dealing with dynamic environments. To improve the performance in dynamic environments, other AIA approaches have been developed recently [14-17].
Although it is also absolutely necessary for AIAs to track a moving optimum as closely as possible, our primary goal remained at the determination of how to best track changes in the environment, which requires an appropriate combination of dynamics for local and global adaptation.
3 Immune response and its algorithm
3.1 Immune response metaphors
Generally, immune response reflects on how antibodies learn antigenic structure patterns and ultimately eliminate antigens. Germinal centers (GCs) are essential elements of immune response, as specialized environments in the B-cell follicle that allow for somatic mutations and extensive proliferation of B lymphocytes [18]. Due to high rates of B-cell division, somatic mutation and selection, GCs occur in highly dynamic environments. Figure 1 [19] illustrates the dynamics of a single GC. In a primary immunization, some B cells respond to the presented antigen and thus are activated. These active cells might migrate to follicular dendritic cells (FDCs) in lymphoid tissues. GCs in the FDC environment can result in a rapid increase in number of B cells. This is called B-cell cloning proliferation. After proliferation, centroblasts differentiate to centrocytes C, which can bind antigens to become C*. The second stage of selection involves a cognate interaction with GC T cells. Antigen-presenting centrocytes C* that fail to make a cognate interaction with a GC T cell die by apoptosis. The remaining cells either regain the centroblast phenotype or simply leave the GC to populate the memory.

Fig.1 Model of GCs reaction
In summary, several vital immune response metaphors, i.e., clonal selection, cell reproduction, somatic mutation, recruitment and immune memory, have been considered. Since antigens outside our bodies are dynamic, immune cells that protect our bodies can react dynamically. This provides us with new ideas for ways to simulate the dynamic environments. By producing several colonies of B cells, these colony cells will evolve independently through different degrees of hypermutation operation; in the meantime, new B cells from bone marrow will be infused to the clones. This provides us with a biological foundation for imitating multi-colony and colony diversity. The degree of hypermutation of B cells is mainly under the influence of the affinities between the antigens and the antibodies produced by the B cells. Specifically, the hypermutation rate of B cells will be low if the related affinities are high, and vice versa. Therefore, we would set different hypermutation rates for various B-cell colonies. Finally, some antibodies from the bone marrow replace the clones with lower affinities, and high-affinity antibodies, also regarded as memory cells related to the intruding antigen, are selected to reproduce some clones, which enhances their affinities through hypermutation. These are evolutionary processes that inspire us to propose optimization algorithms with dynamic environments to solve DEOs.
3.2 Algorithm formulation
AIDE, which adopts some important operations from immune responses of the GCs, is based on multi-population mechanism to satisfy local and global adaptation in searching process. The main framework is shown in Fig.2.
Assume that the population is a set of cells, and each of them represents a solution to the optimization problem. The main procedures of AIDE are listed as follows.
(2)1) A random initial population A0 of size N is created. Let the initial memory cell set Mn be empty and its maximum size be Mm. Set a counter, g=1.
(3)2) Perform fitness evalution of the population.
3) Evenly classify the population into three colonies according to their sorted fitness values, i.e., high fitness colony (HFC) BN1, moderate fitness colony (MFC) BN2 and low fitness colony (LFC) BN3.
4) For each colony, execute dynamical cloning to obtain a series of clonal subpopulations ![]() (i=1, 2, 3) and generate clonal population CN.
(i=1, 2, 3) and generate clonal population CN.
5) Execute somatic mutation on all these clonal subpopulations, and obtain ![]() (i=1, 2, 3).
(i=1, 2, 3).
6) Perform clonal selection on subpopulations ![]() (i=1, 2, 3) so that higher affinity antibodies are picked up. All these form
(i=1, 2, 3) so that higher affinity antibodies are picked up. All these form ![]() (i=1, 2, 3).
(i=1, 2, 3).
7) Utilize population suppression on ![]() (i=1, 2, 3) to eliminate identical and similar antibodies; hence obtain
(i=1, 2, 3) to eliminate identical and similar antibodies; hence obtain ![]() (i=1, 2, 3).
(i=1, 2, 3).

Fig.2 Framework of AIDE algorithm
8) Utilize recruitment on ![]() (i=1, 2, 3) to obtain An+1.
(i=1, 2, 3) to obtain An+1.
9) Put the best antibodies from An+1 into memory pool Mn.
10) If the termination criterion is satisfied, the memory cells in Mn are the desired solutions, and this procedure ends; otherwise, set g=g+1, and return to 2).
In order to discover rapidly the optimum of an moving environment, AIDE, combined with biological mechanism of immune response, the major operations are as follows.
3.2.1 Immune cloning operator
The determination of individuals cloning multiple is one of the important problems in AIAs. Traditionally, the cloning multiples are constant during the searching process or determined only by their fitnesses, without considering the interactions of their antibodies. However, from the immune responses of the GCs, the stimulation level of the antibody to be cloned is determined by both active and suppressive effects of the antigens-antibodies network. Usually, an antigen represents an optimization problem itself, i.e., the objective function and its constraints, and each antibody represents a solution to the optimization problem. As for N antibodies in the evolutionary population of an optimization problem, all antibodies are presented by their real-code with length L. According to Jena’s immune network theory, the stimulation and inhibition between two antibodies could be described as Eqs.(3) and (4):
 (3)
(3)
 (4)
(4)
where function d( ) is the normalized hamming distance between the two bodies:
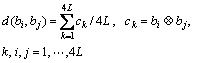 (5)
(5)
D is a threshold. To balance the stimulation and suppression between the antibodies, usually D is set to be 0.5.
The stimulation for the i-th antibody is
![]() (6)
(6)
where ![]() is the normalized objective function. So, the overall stimulus level of the i-th antibody can be expressed as
is the normalized objective function. So, the overall stimulus level of the i-th antibody can be expressed as
![]() (7)
(7)
![]()
![]() and
and ![]() refer to the concentrations of the antibodies. For antibody i, its concentration is calculated by the following equation:
refer to the concentrations of the antibodies. For antibody i, its concentration is calculated by the following equation:
![]()
![]() ,
, ![]() (8)
(8)
Sigmoid function [20] can describe the expansion characteristics of antibodies. In Fig.3, pr states that low level of motivation has very low replication level, rq states that the clonal expansion of antibodies takes place when the motivation reaches a certain degree; op states that the number of antibodies reduces when inhibition is more than motivation. Thus, the cloning operation can be expressed as
![]() (9)
(9)
where kc is the cloning coefficient, usually set between 5 and 10. Nc(i) is the cloning multiple for the i-th antibody.

Fig.3 Clone expansion representation of antibodies
3.2.2 Multi-scale variation strategy
Lack of diversity is the most difficult problem to solve for dynamic optimization [21], and multi- population is one of the principle mechanisms for handling diversity maintenance [22]. A methodology for a dynamic optimizer was first introduced by BLACKWELL and BRANKE and was inspired by BRANKE’s own self-organizing scouts (SOS) [23]. A subpopulation is one part of the populations that track the best solution available and leave the others to search for and track sub-optimal solutions. Following the biological immune response, B cells from GCs expand from several colonial cells through various processes of cloning and hypermutation. Considering this, AIDE for DEOs, which is based on AIAs, averages the sorted immune cells and sorts them into three subpopulations: a high-fitness population, a moderate-fitness population and a low-fitness population. MORRISON and DE JONG [24] proved that larger mutation bursts track the optimum better when the environmental changes are frequent, while lower mutation levels perform better when the changes are slighter. Thus, a multi-scale variation strategy is introduced in this work. The high-fitness population, which is derived by tracking the best solutions available, will be given small-scale variation, while moderate and low fitness populations, which both search for and track the new peaks, will be given moderate and high-scale variation, separately. The multi-scale variation model is
![]() (10)
(10)
 (11)
(11)
where x and x′ are individuals before and after mutation. In this equation, μ is a multi-scale mutation coefficient, C(0, 1) means the standard Cauchy distribution, and γ is a real constant number selected as (1, 2). The variables BN1(g), BN2(g) and BN3(g) refer to high fitness, moderate fitness and low fitness populations, respectively. Different subpopulations A(g) relate to different mutation levels. Furthermore, fmax(A(g)) and favg(A(g)) are related to the maximum and average population fitness of the current generation, respectively. Attenuation factor τ can be selected as [-2, 0]. From the above, we can see that the degree of individual mutation is mainly under the influence of their fitness.
3.2.3 Gradient-based diversity operator
For DEOs, the fitness function is deterministic at any point of time, yet is dependent on time. As a consequence, the optimum changes over time. Thus, the evolutionary algorithm should be able to continuously track the changing optimum rather than requiring a repeated restart of the optimization process. The challenge here is to reuse information from previous environments to speed up the optimization after the change. Although AIAs have shown good results for DEOs, the solution is entirely provided by computational brute force. Instead of using only brute force, numerical information regarding the system, obtained as a by-product of assessments of dynamic optimization function solution, will lead to a significant reduction in the number of clones, and consequently in the computing effort. The simple numerical data to be used are the first order derivatives or gradient, which is presented as
 (12)
(12)
where p is the number of function variables; f ′(x1, x2, …, xp) is the normalized objective function to be optimized, x1, x2, …, xp are function variables and ?xk (k=1, 2, …, p) is a random and limited increment applied to xk (k=1, 2, …, p).
It is clear that GD represents the system sensitivity around a certain operating point, given a minor disturbance. These sensitivities are assessed for each variable, and the final result defines a vector pointing in the most likely direction to achieve the operation objective. If the GD is used, then only a small number of clones are necessary [25-26], which can speed up the optimization. This is obviously beneficial for dynamic environments.
From Fig.3, we can clearly see that when the population reaches a stable state, the cells interact with each other and perform immune suppression, i.e., some of the similar cells are eliminated to avoid redundancy. Rather than using traditional algorithms, which use a number of randomly generated cells to be added to the current population to explore the fitness landscape, we use individuals with gradient information in this study, represented as
![]() (13)
(13)
where x is a sample of the best 10% individuals from each subpopulation and x* is corresponding individual after gradient transformation. In this equation, ![]() is generalized by inverse matrix. r means a random step size, uniformly generated in the range of [0, 1].
is generalized by inverse matrix. r means a random step size, uniformly generated in the range of [0, 1].
4 Theoretical analysis of AIDE
De?nition 1: Suppose y* is the optimal value of Eq.(1) in space Rp, and y(g) is the satisfactory value at generation g, y(g)=f(x(g)), x(g)![]() c(t). Define ?x(g)= x(g+1)-x(g), e(g)=y*-y(g). Clearly, e(g)>0. The necessary condition for the asymptotically stability for AIDE is ?e(g)=e(g+1)-e(g)<0.
c(t). Define ?x(g)= x(g+1)-x(g), e(g)=y*-y(g). Clearly, e(g)>0. The necessary condition for the asymptotically stability for AIDE is ?e(g)=e(g+1)-e(g)<0.
Theorem 1: If ?e(g)<0 and the changes of satisfactory solutions at each generation satisfy ?x(g)<ζ, where ζ is a real number, then AIDE is asymptotically stable.
Proof: Construct a Lyapunov function,
![]()
then
![]() (14)
(14)
![]()
![]() (15)
(15)
where ![]() . From Definition 1, we get e(g)>0. Obviously, to satisfy ?V(g)<0, the necessary condition is ?e(g)<0.
. From Definition 1, we get e(g)>0. Obviously, to satisfy ?V(g)<0, the necessary condition is ?e(g)<0.
Further, from the Taylor series
![]()
![]() (16)
(16)
![]() (17)
(17)
If ?x(g) is small enough, then o[?x(g)] in Eq.(19) has nothing to do with the symbol of ?e(g). That is,
![]()
So,
![]() (18)
(18)
If ![]() , then
, then
![]() (19)
(19)
To satisfy ![]() , then
, then  , so
, so
 (20)
(20)
Let
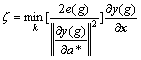
From the above, we get Theorem 1. If and only if ?e(g)<0 and ?x(g)<ζ, then AIDE is asymptotically stable.
However, like other AIAs, AIDE is a stochastic algorithm. It is difficult to control the individuals to evolve strictly along the gradient direction of the objective functions. But, the multiple populations, multi-scale mutation and gradient mechanism make AIDE much more possible for an antibody using a variety of changes in strategy.
From the algorithm described in Section 3.2, we can see: step 1) to step 3), time complexity is O(N); and step 4) to step 7), time complexity is O(Nc?N), where Nc represents the maximum cloning multiple for the antibodies; step 8), new antibodies recruitment, time complexity is O(.1N?p), where, p is the number of function variables. If loop time is g, then the time complexity of AIDE algorithm is O(g?max(Nc, 0.1p)?N).
5 Experimental settings and results
To investigate the performance of AIDE, three other algorithms, i.e., ACO-CSA algorithm [27], population- based arti?cial immune algorithm (PAISA) [11] and dynamic immune networks (Dopt-aiNet)[28], were compared using moving peak experiments.
1) ACO-CSA is a hybrid optimization algorithm based on the fusion of the regular CSA and ACO. The pheromone-based meta-heuristic elitism and hieratical search strategy of the ACO together with the outstanding local search ability and solution diversity characteristics of the CSA are fully combined in ACO-CSA. Dynamic environment simulation results demonstrate that it can achieve an improved performance over both the CSA and ACO, and is a promising algorithm.
2) PAISA is a specific population-based arti?cial immune dynamic algorithm which is based on a set of clonal selection rules and a set of immune memory rules. Its quaternion idea models a dynamic process of human immune response. PAISA is tested on several high dimensional benchmarks and is successfully applied to a practical approximation of a linear system optimization problem.
3) Dopt-aiNet is an extention of Opt-aiNet which is capable of dealing with dynamic environments. The new procedures of Dopt-aiNet include: the use of a modified golden section method as a local search procedure for an optimal mutation rate, two new mutation operators to fine-tune each cell, and a new suppress algorithm based on the approximation of a line between two points that can provide a better measure of the affinity among cells. According to the authors, these additions can improve Opt-aiNet’s ability to find the optimal solutions quickly and maintain the diversity when dealing with dynamic environments.
In all experiments, the population sizes of ACO-CSA and AIDE were 40 and 30, respectively, while those of PAISA, and Dopt-aiNet were 20. The settings of the other parameters to obtain satisfactory performance results are presented in Table 1 for the above algorithms.
Table 1 Settings of parameters

The Moving Peaks Benchmark by BRANKE [29] is usually used for the dynamic test. The base landscape of the Moving Peaks function consists of mo peaks defined in the n-dimensional real space as
 (21)
(21)
where Wi(t) and Hi(t) are the height and width of peak i at time t, respectively, and xij(t) is the j-th element of the location of peak i at time t. Each peak can independently change its height and width and move its location around in the search space. The test function has five peaks defined on a five-dimensional real space. For every generation, the height and width of each peak are changed by adding a random Gaussian variable, and the location of each peak is moved by a shift vector ωi(t) of fixed length s. More formally, a change of a single peak can be described as

![]() (22)
(22)
where the shift vector ωi(t) is a linear combination of a random vector r and the previous shift vector ωi(t-1) and is normalized to length s. The random vector r is created by drawing random numbers for each dimension and normalizing its length to s. The parameter λ allows controlling whether changes exhibit a trend (λ is always set to be 0.5 in our experiments). The settings of parameters for moving peaks are presented in Table 2.
Table 2 Settings of parameters for moving peaks

A total of 400 generations and 40 independent experiments were carried out to study the behaviors of the four algorithms when dealing with a dynamic function. To compare different approaches in a dynamic environment, a reasonable alternative is to report on offline performance [7], which averages the tracking error found at each generation. More precisely, the offline performance of a run with a total of T generations is defined as
![]() (23)
(23)
where R refers to the number of running, ![]() is the best solution found since the last change of the environment and ft is the actual global optimum. In our Moving Peaks tests, we compared AIDE with ACO-CSA [27], PAISA [11], and Dopt-aiNet [28]. In the tests, ten continual environments are taken into consideration. Each environment keeps no change within 5 s. The performance comparison results of ACO-CSA [27], PAISA [11], and Dopt-aiNet [28] when being applied to the dynamic problems described above are shown in Table 3. Accordingly, for each algorithm, the maximum (Best), the minimum (Worst), on-line performance (On-line) and the Shannon entropy (Entropy) results found in each environment are used for comparison. The Entropy in our tests was used to measure disorder/diversity in the population (i.e., entropy is 0 for a fully converged population), which increases when tracking of the changing environment is triggered. For the sake of graphical display, we define Entropy as
is the best solution found since the last change of the environment and ft is the actual global optimum. In our Moving Peaks tests, we compared AIDE with ACO-CSA [27], PAISA [11], and Dopt-aiNet [28]. In the tests, ten continual environments are taken into consideration. Each environment keeps no change within 5 s. The performance comparison results of ACO-CSA [27], PAISA [11], and Dopt-aiNet [28] when being applied to the dynamic problems described above are shown in Table 3. Accordingly, for each algorithm, the maximum (Best), the minimum (Worst), on-line performance (On-line) and the Shannon entropy (Entropy) results found in each environment are used for comparison. The Entropy in our tests was used to measure disorder/diversity in the population (i.e., entropy is 0 for a fully converged population), which increases when tracking of the changing environment is triggered. For the sake of graphical display, we define Entropy as
![]()
![]() (24)
(24)
where 4L is the length of the bit string code and N is the size of individuals for group set A={a1, a2, …, aN}, aj={a1j, a2j, …, aLj}![]() A, j=1, 2, …, N. The curves of the average results of the eight environments for all algorithms are displayed in Fig.4, where the Best, Worst, On-line and Entropy results for different algorithms are displayed in Figs.4(a), (b), (c), and (d). In addition, each experimental result is averaged by 40 runs with the same set of different random seeds.
A, j=1, 2, …, N. The curves of the average results of the eight environments for all algorithms are displayed in Fig.4, where the Best, Worst, On-line and Entropy results for different algorithms are displayed in Figs.4(a), (b), (c), and (d). In addition, each experimental result is averaged by 40 runs with the same set of different random seeds.
In Table 3, we can easily see the different superiorities of these algorithms. As associated with the average fitness results, AIDE is closest to the global value with environments from 1 to 10. Dopt-aiNet which is based on opt-aiNet immune networks, can maintain the population diversity to some extent, and gets the better results as well. However, among the four algorithms, ACO-CSA gets the worst results. As far as the average number of function evaluations is concerned, ACO-CSA performs the fewest, AIDE is the second and PAISA performs the most.
Figure 4(d) shows some results of AIDE in the Moving Peaks tests. The lines indicating population Entropy in Fig.4(d) show that AIDE introduces higher diversity into the population than the other three algorithms when the environments change. By comparing the Best and On-line results shown in Fig.4, it is clear that only AIDE is able to follow the dynamic of the environment. This is in contrast with ACO-CSA, which could barely ?nd the optimum and ?tness slowly dropped as a result of premature convergence. PAISA based on immune mechanism is able to maintain the diversity of the population, but the number of fitness evaluations, as shown in Table 3, is much greater than that of the other algorithms. Therefore, PAISA obtains solutions at a higher computational cost, which is negative for dynamic function optimization. Figure 4(b) shows the results of PAISA. Dopt-aiNet, which uses a separate memory population, a search procedure for controlling decay, new mutation operators and a different measure of affinity, can follow the dynamic environment more flexibly. Figure 4(c) shows the results of Dopt-aiNet for dynamic function optimization.
Table 3 Comparisons of statisfic results for moving peaks


Fig.4 Comparisons of best and worst individuals, on-line performance and entropy results by averaging 40 runs for four algorithms in eight environments: (a) ACO-CSA; (b) PAISA algorithm; (c) Dopt-aiNet algorithm; (d) AIDE algorithm
6 Conclusions
1) A novel dynamic algorithm, AIDE, is introduced, which is based on biological immune responses for global numerical optimization. AIDE models the dynamic process of artificial immune response with operators such as dynamic cloning, multiple populations and multi-scale mutation and gradient-based diversity schemes. The theoretical analyses show that AIDE can converge to the global optimum.
2) Based on the Moving Peak Benchmarks [29], experiments are carried out to compare the performance of several dynamic environment optimization algorithms including the proposed AIDE in dynamic environments. Multiple populations, multi-scale variation strategy and immune cloning operator provide AIDE with higher diversity and adaptability than traditional AIAs and can improve the performance of AIDE in dynamic environment. Moreover, the gradient-based diversity operator, which represents the system sensitivities and the most likely direction to achieve the operation objective, can speed up the optimization and is beneficial for dynamic environment.
References
[1] BRANKE J. Evolutionary optimization in dynamic environments [M]. Kluwer Academic Publishers, 2001: 10-12.
[2] BACK T U H. Evolution strategies applied to perturbed objective functions [C]// Proceedings of the Congress on Evolution Computing. Orlando, Florida, USA, 1994: 40-45.
[3] ANGELINE P J. Tracking extrema in dynamic environments [C]// Proceedings of the Evolutionary Programming VI. London, UK, 1997: 335-345.
[4] BRANKE J, KAU?LER T, SCHMIDTH C. A multi-population approach to dynamic optimization problems [C]// Proceedings of the 5th International Conference on Adaptive Computing in Design and Manufacturing. Plymouth, UK, 2000: 299-308.
[5] YANG S. Memory-based immigrants for genetic algorithms in dynamic environments [C]// Proceedings of the 2005 Genetic and Evolutionary Computation Conference. New York, NY, USA, 2005: 1115-1122.
[6] YANG S, YAO X. Experimental study on population-based incremental learning algorithms for dynamic optimization problems [J]. Soft Computing, 2005, 9(11): 815-834.
[7] YAOCHU JIN, BRANKE J. Evolutionary optimization in uncertain environments-a survey [J]. IEEE Transactions on Evolutionary Computation, 2005, 9(3): 303-317.
[8] DE CASTRO L, VON ZUBEN F. Artificial Immune Systems: PART II-A survey of applications [R]. DCA-RT, 2000.
[9] GASPAR A, COLLARD P. From gas to artificial immune systems: Improving adaptation in time dependent optimization [C]// Proceedings of the Congress on Evolutionary Computation. Washington D C, USA, 1999: 1859-1866.
[10] WALKER J, GARRETT S. Dynamic function optimization: comparing the performance of clonal selection and evolution strategies [C]// The Second International Conference in Artificial Immune Systems. Berlin, Germany, 2003: 273-284.
[11] GONG Mao-guo, JIAO Li-cheng, ZHANG Xiang-rong. A population-based arti?cial immune system for numerical optimization [J]. Neurocomputing, 2008, 72(12): 149-161.
[12] DE CASTRO L, TIMMIS J. An artificial immune network for multimodal optimization [C]// Congress Evolutionary Computation. New York, NY, USA, 2002: 699-704.
[13] DE FRANCA F, ZUBEN F J V, de CASTRO L N. An artificial immune network for multimodal function optimization on dynamic environments [C]// Proceeding of GECCO. New York, NY, USA, 2005: 289-296.
[14] LUO Y, LI R, ZHANG W. Dynamic function optimization algorithm based on immune mechanism [J]. Journal of Xi’an Traffic University, 2005, 39(4): 384-388.
[15] SIMOES A, COSTA E. An immune system-based genetic algorithm to deal with dynamic environments: Diversity and memory [C]// Proceeding of the Sixth International Conference on Neural Networks and Genetic Algorithms. Roanne, France, 2005: 168-174.
[16] ZHANG Zhu-hong, QIAN Shu-qu. Immune algorithm with dynamic environments and its application to greenhouse control [J]. Optim Eng, 2008, 11(1): 125-144.
[17] TROJANOWSKI K, WIERZCHON S T. Immune-based algorithms for dynamic optimization [J]. Information Sciences, 2009, 179: 1495-1515.
[18] FARMER J D, PACKARD N H, PERELSON A S. The immune system, adaptation, and machine learning [J]. Physica, 1986, 22(3): 187-204.
[19] KESMIR C, BOER R. A mathematical model on germinal center kinetics and termination [J]. The Journal of Immunology, 1999, 163(5): 2463-2469.
[20] SUN Yong-zhi, DAI Xiao-hui, WEI Wei. Model of artificial immune response [J]. Journal of Zhejiang University: Engineering Science, 2004, 38(6): 682-685.
[21] BLACKWELL T. Particle swarm optimization in dynamic environments [J]. Studies in Computational Intelligence, 2007, 51: 29-49.
[22] PARROTT D, LI X. A particle swarm model for tracking multiple peaks in a dynamic environment using speciation [C]// Congress on Evolutionary Computation. New York, NY, USA, 2004: 98-103.
[23] BRANKE J, KAU?LER T, SCHMIDT C. A multi-population approach to dynamic optimization problems [M]// Adaptive Computing in Design and Manufacturing, 2000.
[24] MORRISON R W, JONG D E. Triggered hypermutation revisited [C]// Congress on Evolutionary Computation. New York, NY, USA, 2000: 1025-1032.
[25] GERAIS M. A gradient-based artificial immune system applied to optimal power flow problems [J]. LNCS, 2007, 4628: 1-12.
[26] PradyumnKumarShukla. Gradient based stochastic mutation operators in evolutionary multi-objective optimization [J]. LNCS, 2007, 4431: 58-66.
[27] WANG X, GAO X Z, OVASKA S J. A Hybrid optimization algorithm based on ant colony and immune principles [J]. International Journal of Computer Science & Applications, 2007, 4(3): 30-44.
[28] DE FRAN?A F O. VON ZUBEN F J, DE CASTRO L N. An arti?cial immune network for multimodal function optimization on dynamic approach [C]// Proceedings of the Genetic and Evolutionary Computation Conference. GECCO 2005. New York, NY, USA, 2005: 289-296.
[29] BRANKE J. Memory enhanced evolutionary algorithm for changing optimization problems [C]// Proceedings of the Congress on Evolutionary Computation. Washington D C, USA, 1999: 1875- 1882.
(Edited by YANG Bing)
Foundation item: Project(60625302) supported by the National Natural Science Foundation for Distinguished Young Scholars of China; Project (2009CB320603) supported by the National Basic Research Program of China; Projects(10dz1121900, 10JC1403400) supported by Shanghai Key Technologies R&D Program; Project supported by the Fundamental Research Funds for the Central Universities in China; Project(200802511011) supported by the New Teacher Program of Specialized Research Fund for the Doctoral Program of Higher Education in China; Project(Y1090548) supported by Zhejiang Provincial Natural Science Fund, China; Project(2011C21077) supported by Zhejiang Technology Programme, China; Project(2011A610173) supported by Ningbo Natural Science Fund, China
Received date: 2010-07-19; Accepted date: 2010-11-29
Corresponding author: QIAN Feng, Professor, PhD; Tel: +86-21-64252056; E-mail: fqian@ecust.edu.cn

