光电跟踪伺服系统多次跟踪控制方法
董浩，霍炬
(哈尔滨工业大学 控制与仿真中心，黑龙江 哈尔滨，150080)
摘要：为提高输入信号未知条件下伺服系统跟踪性能，提出多次跟踪控制方法。研究多次跟踪控制方法的结构、理想情况下系统特点、多次跟踪系统的实现方案以及理想情况下多次跟踪部分的作用。应用于光电跟踪伺服系统，大幅提高系统型别及跟踪精度。实验结果表明：采用3次跟踪控制方法，系统达到Ⅴ型，跟踪匀加加速度无静差；在跟踪探测器输出延迟0.04 s情况下，对最大速度为50 (°)/s、最大加速度为30 (°)/s2的等效正弦信号稳态跟踪精度小于1′，比PI控制下系统的跟踪精度提高30倍。
关键词：多次跟踪；等效复合控制；前馈； 高型系统；光电跟踪
中图分类号：TP273 文献标志码：A 文章编号：1672-7207(2011)S1-0281-07
Multiple tracking control for opto-electrical tracking servo system
DONG Hao, HUO Ju
(Control & Simulation Center, Harbin Institute of Technology, Harbin 150080, China)
Abstract: A multiple tracking control method was generated to improve the tracking performance of a servo system. The multiple tracking control structure, system characteristic on ideal condition and the effect of multiple tracking parts were researched. The results show that when it is applied in opto-electrical tracking servo system, it raises system type and improved the tracking precision. A cubic tracking control which made a V type system is designed. The tracking precision of a servo system on the cubic tracking control reaches 1′, which is 30 times higher than that of a PI control when the target moves at a maximum rate of 50 (°)/s angular velocity with a maximum of 30 (°)/s2 angular acceleration.
Key words: multiple tracking; equivalent compound control; feed forward; high type system; opto-electrical tracking
光电跟踪伺服系统具有捕获瞄准功能，广泛应用于航天、航空、地面设备中[1-2]。由于跟踪探测输出存在延迟，跟踪回路带宽受到限制，增益难于提高，因此跟踪精度较低。若直接将回路校正为高型，受实际对象饱和特性影响，存在条件稳定问题且系统在干扰作用下会出现大幅震荡[3]。当系统型别大于2时，除复合控制系统外，使系统稳定是相当困难的，因此除航天及航天控制系统外，Ⅲ型及Ⅲ型以上的系统几乎不采用[4]。Lin等[5-8]采用的切换方法解决该问题，即大偏差时采用低增益控制使系统快速收敛，小偏差时采用高增益控制保证系统性能。
按输入进行补偿的复合控制是提高伺服系统型别与性能的常用方法，但是在光电跟踪过程中，探测设备只提供偏差信号，目标运动参数(位置、速度、加速度)未知且不能直接测量，无法直接通过复合控制提高跟踪精度。根据已知信息对运动目标参数进行估计，从而构成等效复合控制是提高系统跟踪精度的有效方法。一是王毅等[9-10]采用伺服系统的位置、速度信息经微分低通滤波后代替目标的速度、加速度进行前馈，形成速度、加速度滞后补偿。李文军等[11]指出该方法会降低系统稳定裕度，甚至使系统处于临界稳定状态。二是Futman等[12]采用卡尔曼滤波估计目标运动位置、速度，构成计算机辅助跟踪，但该方法依赖目标运动模型及状态噪声和量测噪声统计特性。在此，本文作者提出一种等效复合控制结构和前馈控制器的设计方法，可大幅提高系统型别从而提高光电跟踪伺服系统的稳态跟踪精度。
1 多次跟踪控制方法
多次跟踪控制方法是采用开环控制结构、是一种前馈控制方法，但不需要系统输入信息，只需要系统偏差及系统输出信息，且偏差与系统输出信息可以存在延迟。对于无法直接获得输入信号进行前馈控制的场合具有实际意义。
1.1 多次跟踪系统结构
多次跟踪系统结构如图1所示。图1中：P(s)为实际对象；P0(s)为标称对象，称实际对象所在的回路为实际回路，称标称对象所在的回路为标称回路，称控制器Gi所在的回路为标称回路i，i=2，…，n。
多次跟踪结构的特点为：一是所有回路的输入均相同，即yri=yr；二是控制量un与控制器Gn-1输出控制量un-1求和，然后共同作用于标称回路n-1的对象，un，un-1与第控制器Gn-2输出控制量un-2取和共同作用于标称回路n-2的对象，依此类推，最后所有控制器输出控制量之和共同作用于实际回路的对象。多次跟踪系统的任一回路的控制量为其上所有回路控制器输出控制量之和。
多次跟踪系统在输入信号yr未知情况下，采用实际回路偏差及系统输出构成标称回路i偏差，有
(1)
其中：yi′为系统输出分量；y1′为实际对象输出，y1′=y；ei为系统偏差分量，i=1，…，n，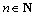
。由于实际回路为一单位负反馈系统，e1是实际对象跟踪误差，也是多次跟踪系统的跟踪误差。
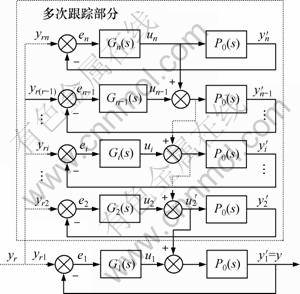
图1 多次跟踪系统结构框图
Fig.1 System diagram of multiple tracking
由于理想情况下系统具有对输入信号跟踪多次的特点，故将其称为多次跟踪控制方法。
1.2 理想情况下多次跟踪特点
理想情况下，标称对象与实际对象完全相等，即P(s)=P0(s)，通过方框图化简得多次跟踪结构等效框图如图2所示。图2中：Wi(s)=Gi(s)P0(s)，i=1，…，n。系统的跟踪误差为：
(2)
即e1仍为系统的跟踪误差。系统误差传递关系为：
(3)
图2 理想情况下多次跟踪系统结构等效框图
Fig.2 Equivalent diagram of multiple tracking on ideal condition
可见：在理想情况下，标称回路n-1的输入信号为跟踪偏差en，标称回路n-2的输入信号为跟踪偏差en-1，…，实际回路的输入信号为前n-1次跟踪系统的跟踪偏差e2，相当于对输入信号跟踪了多次。
对于校正后的线性系统，当输入为某一频率(此频率小于回路开环剪切频率)的正弦信号时，其稳态跟踪偏差为同一频率的幅值降低的正弦信号，将此幅值降低的正弦信号作为输入继续跟踪，则第2次稳态跟踪偏差进一步降低。经多次跟踪，最终稳态跟踪偏差无疑比1次跟踪的小很多，n次跟踪系统的稳态跟踪偏差为对输入信号跟踪n次的偏差。
1.3 输入未知条件下多次跟踪系统的实现方案
只要给定ei(t)与yi′(t)的初值，由式(1)以及控制的闭环作用即可完成多次跟踪控制的计算，以2次跟踪控制为例，给出系统的信号流图如图3所示，多次跟踪系统的实现方案依次递推即可。其开环传递函 数为：
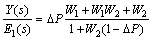
图3 2次跟踪系统的实现
Fig.3 Twice tracking system implementation
其闭环传递函数为：
其中：ΔP(s)=P(s))/P0(s)。由其闭环传递函数可见：只要每一个回路稳定，则系统稳定。
无论ei(t)与yi′(t)的初值如何选取，只要设计的多次跟踪部分是稳定的，则实际回路是稳定的，经过一段时间的过渡过程系统最终均能够收敛到稳态，在输入信号未知条件下可令标称回路偏差、输出的初值与系统偏差、输出的初值相等，即ei(0)=e1(0)，yi′(0)=y(0)。
1.4 理想情况下多次跟踪部分的作用
首先推导多次跟踪部分以及整个系统的输入输出关系，再举例说明多次跟踪部分的作用。通过梅森增益公式得多次跟踪部分的输入输出闭环传递函数为：
(4)
又u2′P0=y2′，得输入到前馈控制量u2′的传递函数为：
(5)
由梅森增益公式得系统的输入输出闭环传递函数为：
(6)
系统误差传递函数为：
(7)
以最简单的积分对象P(s)=1/s为例分析多次跟踪部分的作用。假设控制器G1(s)=6，系统误差传递函数为s/(s+6)，系统为Ⅰ型，取标称对象P0(s)=1/s，控制器G2(s)=G3(s)=6+16/s。
首先考察多次跟踪部分的特性，其输入输出传递函数为：
(8)
输入到前馈控制量u2′的传递函数为：
(9)
由式(9)可见：前馈控制量u2′实质为系统输入信号的微分信号。所以，多次跟踪控制是求取系统前馈控制量的一种设计方法。然后，考察系统的闭环特性，加入多次跟踪部分前，系统的闭环传递函数为：
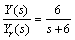(10)
系统误差传递函数为：
(11)
加入多次跟踪部分后，系统的闭环传递函数为：
(12)
系统误差传递函数为：
(13)
系统型别由Ⅰ型提高到Ⅴ型，跟踪精度有很大提高。二者的输入输出闭环bode图如图4(a)所示，输入误差闭环bode图如图4(b)所示。在加入多次跟踪部分后，系统低频段误差传递函数的增益大幅降低，若输入信号的频带小于1 rad，则系统稳态跟踪精度将得到大幅提高。
图4 加入多次跟踪部分前后系统bode图
Fig.4 System bode diagram with and without multiple tracking
最后考察系统的跟踪误差。假设输入信号为正弦信号yr=83.3°sin(0.6t)，加入多次跟踪前系统稳态跟踪误差的幅值为：
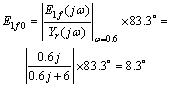(14)
加入多次跟踪部分后跟踪误差为：
(15)
可见：多次跟踪部分大幅提高了系统对正弦信号的稳态跟踪精度。
所以，理想情况下采用多次跟踪控制结构设计的前馈控制器的作用是提供输入信号经过整合的微分信号，在该信号作用下系统的型别得到提高，从而系统的稳态跟踪精度大幅提高。
2 光电跟踪伺服系统多次跟踪控制
光电跟踪伺服系统通常由电流环、速率稳定回路，位置跟踪回路构成[10]，伺服系统结构如图5所示。通常速率稳定环带宽大于20 Hz，其闭环特性可等效为低通环节，跟踪回路带宽一般小于3 Hz。
图5 普通光电跟踪伺服系统结构框图
Fig.5 Ordinary opto-electrical servo system diagram
跟踪回路的低带宽限制使回路增益难以提高，而运动目标未知，无法通过前馈来提高跟踪精度，因此，这里对位置跟踪回路采用多次跟踪。由1.1节知，只要存在标称对象、标称回路偏差以及标称回路控制器，就可以构成多次跟踪系统。
2.1 多次跟踪的标称对象特性
由图5可知：光电跟踪平台速度回路闭环特性为1/(Tvs+1)，低频段近似为比例环节1，因此取标称多次跟踪的标称对象模型为积分环节P0(s)=1/s。
标称对象模型与实际对象存在差别，为使得实际对象特性与标称对象特性相等，采用文献[2]给出的反馈型扰动观测器进行补偿，如图6所示。图6中：Q(s) 为一阶低通滤波器，低频段Q→1，在Q(s)频段内系统从u到y的闭环传递函数等于标称对象的特性P0(s)。
图6 反馈型扰动观测器
Fig.6 Disturbance observer
2.2 多次跟踪系统的标称回路偏差
跟踪过程中，目标状态(位置、速度、加速度等信息)并不已知，即系统输入yr未知，考虑到e1本身存在延迟，由式(1)可得标称回路偏差为ei=e1+(y-y′i)e-τs，其中：τ为延迟时间。延迟将影响标称回路与实际回路的相位裕度，对低频信号的稳态跟踪精度没有影响。
2.3 多次跟踪控制器
为保证实际系统饱和条件下具有良好的稳定性，实际跟踪回路采用P控制。为防止噪声影响过大，采用尽可能少的跟踪回路并使回路带宽尽可能低，为提高跟踪精度，标称回路的控制器采用PI控制器。
最后给出光电跟踪伺服系统的多次跟踪控制结构框图如图7所示。
图7 光电跟踪伺服系统多次跟踪控制结构图
Fig.7 Diagram of multiple tracking control for opto-electrical servo system
3 仿真与实验
系统要求：跟踪探测器采样频率50 Hz，输出滞后2帧，跟踪速度≤50 (°)/s，加速度≤30 (°)/s2，目标误差≤1′。
取输入信号为最大速度50 (°)/s、最大加速度30 (°)/s2的等效正弦信号yr=83.3°sin(0.6t)。根据伺服系统速度闭环特性实测结果设仿真对象参数为Tv=0.01，速度回路闭环带宽约为20 Hz。
3.1 多次跟踪控制方法提高稳态跟踪精度仿真
考虑噪声、扰动及伺服系统精度等因素，采用3次跟踪方法。实际回路采用P控制，跟踪控制器G1=6；标称回路采用PI控制，跟踪控制器G2=G3=6+16/s。0.04 s延迟作用下实际回路开环剪切频率为6.07 rad，相位裕度为76°，标称回路的开环剪切频率为6.42 rad，相位裕度为43.6°。
普通PI控制取Kp0=11.5，Ki0=66，0.04 ms延迟下系统剪切频率为13.1 rad，相位裕度为35°。
为比较跟踪效果，给出PI控制，PI+速度滞后补偿控制以及多次跟踪的跟踪误差，仿真结果如图8所示，稳态跟踪误差比较如表1所示。
图8 跟踪误差仿真结果
Fig.8 Simulation of tracking error
表1 等效正弦稳态跟踪误差比较
Table 1 Comparison of equivalent sine tracking errors
仿真结果表明：采用3次跟踪，光电跟踪伺服系统稳态跟踪精度小于0.3′，比无补偿控制精度提高90倍，比PI控制+速度滞后补偿精度提高21倍，可以达到跟踪误差≤1′的要求。
3.2 多次跟踪控制方法提高稳态跟踪精度测试
由于暂时不具备光电平台实验条件，采用文献[10]所述方法，将普通伺服系统的偏差信号人为延迟40 ms进行测试，得伺服系统的稳态跟踪误差曲线如图9所示。
由图9可见：试验稳态跟踪误差小于0.8′，误差较大且存在尖峰。观察误差曲线包络可知实际跟踪控制的误差小于0.5′，与仿真结果比较相差较大，主要是模型参数不确定因素造成的：一是对伺服系统速度频率特性测试本身存在偏差；二是转动过程中转动惯量并不恒定，存在一定的变化。试验误差曲线的尖峰，主要是干摩擦引起的执行机构死区因素造成的。
王建立等[10]在延迟20 ms条件下所得测试精度小于1′，而采用多次跟踪控制方法在40 ms条件下对相同机动目标达到了更高的测试精度。
图9 3次跟踪稳态跟踪误差测试结果
Fig.9 Test of tracking error under cubic tracking
3.3 多次跟踪系统型别测试
采用3次跟踪方法，在1个P控制器、2个PI控制器作用下系统为Ⅴ型，伺服系统跟踪匀加速度信号无静差，跟踪匀加速度信号稳态误差为常值，伺服系统输出如图10所示，跟踪误差如图11所示。
受伺服系统的最大速度限制以及分辨率限制，测试时减小了各个控制器的参数，否则，理论跟踪误差将小于最小分辨率，无法获得正确的测试结果。取输入信号yr=10t4和yr=t5，单位是脉冲个数。
伺服系统跟踪信号10t4稳态偏差趋近于0，跟踪信号t5稳态偏差约为常值480个脉冲。可见：采用3次跟踪控制方法，可将伺服系统型别提高到Ⅴ型。
图10 伺服系统输出曲线
Fig.10 Output of servo system
图11 伺服系统跟踪误差曲线
Fig.11 Tracking error of servo system
4 结论
(1) 采用多次跟踪控制方法设计的前馈控制器，可在输入信号未知条件下对其进行微分，用该微分信号进行前馈，可大幅提高系统型别以及系统合成带宽，从而提高光电跟踪伺服系统的稳态跟踪精度。
(2) 本文只给出了理想情况下多次跟踪系统的特性，并采用补偿方法获得这一理想条件，对伺服系统进行验证。在非理想情况下，存在模型参数不确定性时系统的特性需要进一步研究。
参考文献：
[1] Hilkert J M. Inertially stabilized platform technology concepts and principles[J]. IEEE Contr Syst Mag, 2008, 28(1): 26-46.
[2] Masten M K. Inertially stabilized platforms for imaging optical systems[J]. IEEE Contr Syst Mag, 2008, 28(1): 47-64.
[3] 王广雄, 何朕. 控制系统设计[M]. 北京: 清华大学出版社, 2008: 121-122, 153-154.
WANG Guang-xiong, HE Zhen. Control system design[M]. Beijing: Tsinghua University Press, 2008: 121-122, 153-154
[4] 胡寿松. 自动控制原理[M]. 北京: 科学出版社, 2001: 120-121.
HU Shou-song. Automatic control principle[M]. Beijing: Science Press, 2001: 120-121.
[5] Lin Z, Saberi A. Semi-global exponential stabilization of linear systems subject to “input saturation” via linear feedbacks[J]. System & Control Letters, 1993, 21(3): 225-239.
[6] Lin Z. Semi-global stabilization of linear systems with position and rate limited actuators[J]. Systems & Control Letters, 1997, 30: 1-11.
[7] Lin Z, Saberi A. Semi-global exponential stabilization of linear discrete-time systems subject to input saturation via linear feedback[J]. Systems & Control Letters, 1995, 24(2): 125-132.
[8] Lin Z, Stoorvogel A A, Saberi A. Output regulation for linear systems subject to input saturation[J]. Automatica, 1996, 32(1): 29-47.
[9] 王毅, 魏忠和. 补偿伺服系统速度误差和加速度误差的方法[J]. 光学精密机械, 1973, 13: 21-25.
WANG Yi, WEI Zhong-he. Methods to compensate the velocity error and acceleration error for servo systems[J]. Optic Machine, 1973, 13: 21-25.
[10] 王建立, 吉桐伯, 高昕, 等. 加速度滞后补偿提高光电跟踪系统跟踪精度的方法[J]. 光学精密工程, 2005, 13(6): 681-685.
WANG Jian-li, JI Tong-bo, GAO Xin, et al. Study of improving the optoelectronic system capability to track moving targets by using acceleration delay compensation[J]. Optics and Precision Engineering, 2005, 13(6): 681-685.
[11] 李文军, 赵金宇, 陈涛. 速度滞后补偿参数对光电伺服系统的影响分析[J]. 测试技术学报, 2005, 19(1): 70-74.
LI Wen-jun, ZHAO Jin-yu, CHEN Tao. Analysis of the effect of velocity delay compensation parameters on photo-electric servo systems[J]. Journal of Test and Measurement Technology, 2005, 19(1): 70-74.
[12] Futman P, Velger M. Tracking targets using adaptive Kalman filtering[J]. IEEE Trans Aerosp Electron Syst, 1990, 26(5): 691-698.
(编辑 杨幼平)
收稿日期：2011-04-15；修回日期：2011-06-15
通信作者：董浩(1980-)，男，河北唐山人，博士研究生，从事光电跟踪、伺服系统控制技术研究；电话：15945995186；E-mail：donghao-email@163.com
