文章编号：1004-0609(2014)12-3009-07

V-5Cr-5Ti合金高温变形本构模型

曲凤盛，王震宏，张  浩

(中国工程物理研究院，绵阳 621900)

摘  要：采用热物理模拟试验机研究V-5Cr-5Ti在变形温度为1150~1400 ℃和应变速率为0.001~1 s^-1条件下的热变形行为。采用双曲正弦函数建立V-5Cr-5Ti合金高温条件下的本构方程，通过六次多项式拟合的方法将应变引入到本构方程中。结果表明：V-5Cr-5Ti合金真应力-应变曲线表现出动态再结晶和动态回复两种软化机制。流变应力随着应变速率的增加而增大，随温度的升高而减小。采用应变的六次多项式拟合得到的本构关系中，流变应力预测值与实验值吻合较好，绝大多数(94%)情况下预测的误差小于6.4%，平均相对误差仅为2.84%。

关键词：V-5Cr-5Ti；热压缩；本构方程；流变应力

中图分类号：TG146.4                　   　     文献标志码：A

Constitutive modeling for high temperature flow behavior of V-5Cr-5Ti alloy

QU Feng-sheng, WANG Zhen-hong, ZHANG Hao

(China Academy of Engineering Physics, Mianyang 621900, China)

Abstract: The flow stress behaviors of V-5Cr-5Ti alloy were investigated at the temperatures of 1150-1400 ℃ and strain rates of 0.001-1 s^-1 using thermo-simulation machine. The constitutive equations of flow stress of V-5Cr-5Ti alloy at high temperature were established by utilizing hyperbolic sine function and introducing the strain factor with six polynomial fitting, then the accuracy of the constitutive equation was verified. The results show that during the hot compression deformation of V-5Cr-5Ti alloy, the characteristics of dynamic recrystallization and dynamic recovery are observed, respectively. The flow stress increases with increasing the strain rate, and decreases with increasing the temperature. The flow stress of V-5Cr-5Ti alloy predicted by the proposed models with 6th order polynomial fitting agrees well with the experimental value, the relative error is lower than 6.4% at the overwhelming majority (94%) cases of the deformation conditions, the average relative error is only 2.84%.

Key words: V-5Cr-5Ti; hot compression; constitutive equation; flow stress

钒基合金是优良的聚变堆用低活性结构材料，同其他金属结构材料相比，钒基合金最显著的优点是其在中子辐照条件下的低激活特性和优良的高温性能 ^[1-6]，因此，钒基合金成为聚变堆中极具吸引力的第一壁候选结构材料。目前，聚变堆用钒合金的研究焦点集中于V-4Cr-4Ti合金和V-5Cr-5Ti合金。研究表明，V-5Cr-5Ti合金在高温力学性能、抗氧化性和抗中子辐照等方面均优于V-4Cr-4Ti合金^[6]。V-5Cr-5Ti合金通常采用二次真空自耗电弧熔炼(VAR)制得，合金晶粒粗大，残余应力较高，无法满足聚变工程对结构材料的要求。而且V-5Cr-5Ti合金属于单相合金，无法采用相变进行晶粒细化，改善组织并提高力学性能，因此，塑性加工是改善组织并提高力学性能唯一途径。铸态V-5Cr-5Ti合金的变形能力即使在高温下也相对有限，而且该合金对变形温度、应变速率及应变量等参数极为敏感，在实际热加工过程中极易产生开裂等失稳现象。另外，钒基合金在高温下容易氧化产生剧毒氧化物V₂O₅，所以在高温下必须对该合金进行特殊保护处理后才能热加工。于兴哲等^[7]采用单轴热压缩法研究了V-5Cr-5Ti合金热变形性能，从裂纹的角度论述了合金合理的热加工参数，但未推导该合金热变形本构方程。在实际压力加工过程中对本构方程进行摸索存在合金制造成本高、研究周期长和技术难度大的缺点。随着计算机技术的快速发展，有限元(FEM)数值模拟方法在减少实验量和提高工作效率等方面起到了重要作用，而建立准确的流变应力模型是提高数值模拟精度的关键。目前，国内外大多采用VAR工艺制备V-5Cr-5Ti合金^[6]，因此，构建铸态V-5Cr-5Ti合金热变形本构方程具有普适意义，能为后续数值模拟优化研究提供准确的依据。由于材料在塑性加工过程中的动态响应是由材料内部组织演化引起的硬化过程和软化过程综合作用的结果，故本构关系是高度非线性的，不存在普遍适用的构造方法。通常依据Arrhenius型方程对实验数据采用数理统计的方法建立本构关系，目前，该方法在镁合金^[8]、铝合金^[9]、钛合金^[10]研究中取得了很好的效果。因此，本文作者将采用Arrhenius方程描述V-5Cr-5Ti合金的本构关系。

1  实验

实验材料为两次真空自耗电弧熔炼后得到铸态V-5Cr-5Ti合金棒。合金的化学成分(质量分数)为：4.78%~4.82% Cr，4.79%~5.21% Ti，0.045% O，0.005%~ 0.006% N，0.006% C。压缩试样直径为10 mm，高度为12 mm，试样均取自合金棒中心等轴晶区。在热物理模拟机上以7 ℃/s的速率加热到变形温度，保温2 min后进行压缩试验，变形温度分别为1150、1200、1250、1300、1350和1400 ℃，应变速率为0.001~1 s^-1，高度压缩率为55%。试样在变形结束后迅速进行水淬以保留高温组织，沿平行压缩轴方向切开试样，机械研磨制备金相试样，采用金相显微镜观察热变形前后的微观组织。

2  结果与讨论

2.1  热压缩曲线

通过热压缩实验得到了不同温度和应变速率下V-5Cr-5Ti合金的真应力-真应变曲线，如图1所示。

图1  不同变形条件下V-5Cr-5Ti合金真应力-真应变曲线

Fig. 1  Curves of true stress-strain for V-5Cr-5Ti alloy under different conditions

从图1可以看出：V-5Cr-5Ti合金在实验所处变形条件下，当应变速率一定时，流变应力随着温度的升高而降低；当变形温度一定时，流变应力随着应变速率的增加而增大。这是由于在应变速率一定时，当变形温度升高，原子的热激活作用加剧，位错的活动能力增强，在变形过程中有更多的位错进行滑移和攀移，从而使软化过程更为突出，流变应力降低；随着应变速率的增加，单位时间内产生的位错密度增加，位错运动受阻，位错攀移及位错反应等引起的软化速率相对降低，硬化增强，从而使合金的临界切应力升高，导致流变应力增大^[11-13]。同时，合金的变形时间缩短，使得单位时间内动态再结晶的形核数目减少，软化程度降低，间接地使合金的流变应力增大。V-5Cr-5Ti合金真应力-应变曲线表现出动态回复和动态再结晶两种软化机制：动态再结晶型曲线有明显的峰值应力，动态回复型曲线无峰值应力。

2.2  本构方程的建立

在金属高温塑性变形过程中，应力主要受变形温度、应变速率和应变量的影响。双曲正弦方程^[14]被广泛地用于描述应力与应变速率和变形温度之间的关系，尤其是在高温下的变形过程。变形温度和变形速率对金属高温塑性变形的影响可以进一步由参数Z来表示^[15]，其数学表达式如下所示：

                              (1)

                      (2)

当≤0.8时，

                                 (3)

当≥1.2时，

                             (4)

当取任意值时，

                         (5)

式中：Z为温度补偿的应变速率因子；为应变速率，s^-1；Q为变形激活能，J/mol；为流变应力，MPa；n为应力指数；T为绝对温度，K；R为摩尔气体常数，8.314 J/(mol·K)；A、n₁、n、和为与材料有关的常数，。

取不同条件下的峰值应力为流变应力，作出和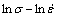关系曲线，并分别进行线性回归，如图2(a)和(b)所示，可得0.008377 MPa^-1。

图2  峰值应力与应变速率的关系曲线

Fig. 2  Relationships between peak stress and strain rate

假定热变形激活能Q在一定温度范围内与T无关，将式(5)带入式(1)进行变换整理可得：

            (6)

做出和关系曲线，并进行线性回归，如图3(a)和3(b)所示，由此可推得变形激活能 kJ/mol。

同样地将式(5)代入式(1)，对数据进行线性回归，如图4所示，可得到，。

将求得的Q、R、和n 值代入式(1)，得到V-5Cr-5Ti合金峰值应力Arrhenius 流变应力本构方程为

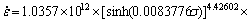
                    (7)

用含Z参数描述流变应力的表达式为

 (8)

图3  与的关系图

Fig. 3  Relational graphs of (a) and (b)

图4  的关系图

Fig. 4  Relational graphs of

2.3  应变量耦合

由图1可知，应变量对V-5Cr-5Ti合金的流变应力有较大的影响，然而式(1)中未能考虑应变量的影响，这会使材料在热变形过程中，的预测值与实际值误差较大。因此，需要建立耦合应变量因素的本构关系。本文作者计算了不同应变量下本构关系模型中的常数，发现材料常数与应变量之间存在复杂的非线性关系。为准确地描述材料常数与应变量之间的关系，假定材料常数(、n、Q和ln A)与应变量存在多项式函数关系，从而实现将应变量嵌入本构模型。一般采用四次多项式^[16-18]对材料进行回归拟合，但V-5Cr-5Ti的材料常数与应变量关系较为复杂，因此本文作者采用文献[19]中六次多项式进行拟合，拟合多项式如下式所示。

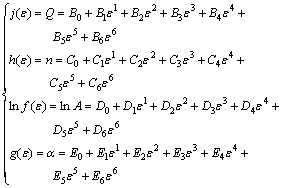(9)

拟合参数结果如表1所列。图5所示为拟合曲线，可以看出，采用6次多项式能够较好地描述材料常数间的非线性关系，而更高的拟合次数会导致“Runge现象”^[20]，而且拟合精度提高不大。

通过确定材料常数可以确定不同应变量下的，故V-5Cr-5Ti合金动态流变应力本构方程为

    (10)

用含Z参数使描述流变应力的表达式为：

        (11)

式中：、、和分别为A、、n和Q在不同温度以及应变速率下的应变多项式函数。

表1  多项式函数的拟合参数

Table 1  Fitting of coefficients of polynomial functions

图5  本构方程中各参数与应变的关系

Fig. 5  Relationships between different coefficients of constitutive equation and strain

2.4  本构关系模型的验证

为验证在不同变形温度、应变速率和应变量下本构关系模型预测流变应力的准确性，对由本构关系计算得到的预测值和实验值进行对比。由图6可知，预测的与实验值在实验条件范围内能够保持较高的一致性。

为了更加准确地描述建立本构关系的精确程度，引入了相关系数R和平均相对误差E_r，其数学式如下所示：

                 (12)

图6  不同应变条件下实测和计算的真应力-真应变曲线

Fig. 6  Calculated and measured stress-strain curves under different strain rates

                          (13)

式中：E为实验值；P为本构关系的预测值；和分别为E和P的平均值；N为实验数据点的数量。相关系数R通常用来分析实验值和计算值的线性关系的强弱，但相关系数并不是越高越好，因为预测数据可能全部偏高或者偏低^[21]。而E_r是通过计算预测值与实验值的平均相对误差得到的，E_r对本构关系可预测性的分析是无偏差的。因此，综合E_r和R可以对预测值与实验值进行准确的评定。

图7所示为本构关系预测值与实验值的相关性，可以看出本构关系的预测值与实验值相关性较好，相关系数R为0.996。并且通过计算实验条件范围内的E_r，得到E_r仅为2.84%。综合R和E_r表明所建立的本构关系具有良好的预测能力。

综上所述，双曲正弦模型能够较好地描述V-5Cr-5Ti合金高温变形的流变行为，采用六次多项式拟合的本构关系具有较高的精度，能够为该合金在数值模拟时提供准确的本构关系。

图7  本构关系预测流动应力值与实验值的相关性

Fig. 7  Correlation between experimental and predicted flow stress data from constitutive equation

3  结论

1) V-5Cr-5Ti合金在高温压缩变形过程中，当变形温度一定时，流变应力随应变速率的增大而增大；当应变速率一定时，流变应力随变形温度的升高而减小。在本实验条件下，V-5Cr-5Ti合金呈现出动态再结晶和动态回复两种软化机制。

2) 建立了含应变量V-5Cr-5Ti合金本构关系模型，采用六次多项式函数可以较好地表达材料常数(、n、Q、ln A)与应变量之间的关系。

3) 本构关系预测值与实验值之间的相关系数为0.996，平均相对误差为2.82%，表明建立的本构关系在实验条件范围内能准确地预测流动应力。

REFERENCES

[1] 于兴哲, 宋月清, 崔 舜, 李 明. 钒基合金的研究现状与进展[J]. 材料开发与应用, 2006, 6: 36-40.

YU Xing-zhe, SONG Yue-qing, CUI Shun, LI Ming. Current state and progress of research on vanadium alloys[J]. Development and Application of Materials, 2006, 6: 36-40.

[2] BLOOM E E, CONN R W, DAVIS J W. Low activation materials for fusion applications[J]. Journal of Nuclear Materials, 1984, 122/123(Part1): 17-21.

[3] SATOU M, ABE K, KAYANO H. High-temperature deformation of modified V-Ti-Cr-Si type alloys[J]. Journal of Nuclear Materials, 1991, 179/181(part1): 757-761.

[4] SMITH D L, CHUNG H M, MATSUI H, ROWCLIFFEC A F. Progress in vanadium alloy development for fusion application[J]. Fusion Engineering and Design, 1998, 41(1/4): 7-14.

[5] NATESAN K, SOPPET W K, UZ M. Effects of oxygen and oxidation on tensile behavior of V-4Cr-4Ti alloy[J]. Journal of Nuclear Materials, 1998, 258/263(Part2): 1476-1481.

[6] CHEN Ji-ming, QIU Shao-yu, YANG Lin, XUA Zeng-yu,DENG Ying, XUA Ying. Effect of oxygen, hydrogen and neutron irradiation on the mechanical properties of several vanadium alloys[J]. Journal of Nuclear Materials, 2002, 302(2/3): 135-142.

[7] 于兴哲, 宋月清, 崔 瞬, 李 明, 李增德. V-5Cr-5Ti合金热压缩模拟实验分析[J]. 稀有金属, 2008, 32(6): 705-708.

YU Xing-zhe, SONG Yue-hui, CUI Sun, LI Ming, LI Zeng-de. Analysis of simulated test of hot compression of V-5Cr-5Ti alloy[J]. Chinese Journal of Rare Metals, 2008, 32(6): 705-708.

[8] 王忠堂, 张士宏, 齐广霞, 王 芳, 李艳娟. AZ31镁合金热变形本构方程[J]. 中国有色金属学报, 2008, 18(11): 1977-1982.

WANG Zhong-tang, ZHANG Shi-hong, QI Guang-xia, WANG Fang, LI Yan-juan. Constitutive equation of thermal deformation for AZ31 magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(11): 1977-1982.

[9] 吴永甫, 李淑慧, 侯 波, 于忠奇. 铝合金7075-T651动态流变应力特征及本构模型[J]. 中国有色金属学报, 2013, 23(3): 658-665.

WU Yong-fu, LI Shu-hui, HOU Bo, YU Zhong-qi. Dynamic flow stress characteristics and constitutive model of aluminum 7075-T651[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(3): 658-665.

[10] 王新平, 李 礼, 张晓泳, 周科朝, 李 超. TC18钛合金变形本构关系及其热轧过程有限元仿真的应用[J]. 中国有色金属学报, 2013, 23(2): 379-388.

WANG Xin-ping, LI Li, ZHANG Xiao-yong, ZHOU Ke-chao, LI Chao. Constitutive relationship and its application in finite element simulation of hot rolling of TC18 titanium alloy[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(2): 379-388.

[11] 张北江, 赵光普, 焦兰英, 胥国华, 秦鹤勇, 冯 涤. 热加工工艺对GH4586合金微观组织的影响[J]. 金属学报, 2005, 41(4): 351-356.

ZHANG Beijiang, ZHAO Guangpu, JIAO Lanying, XU Guohua, QIN Heyong, FENG Di. Influence of hot working process on microstructures of superalloy GH4586[J]. Acta Metallurgica Sinica, 2005, 41(4): 351-356.

[12] 鞠 泉, 李殿国, 刘国权. 15Cr-25Ni-Fe基合金高温塑性变形行为的加工图[J]. 金属学报, 2006, 42(2): 218-224.

JU Quan, LI Dian-guo, LIU Guo-quan. The processing map of hot plastic deformation of a 15cr-25ni-fe base superalloy[J]. Acta Metallurgica Sinica, 2006, 42(2): 218-224.

[13] 李淼泉, 姚晓燕, 罗 皎, 林莺莺, 苏少博, 王海荣. 镍基高温合金GH4169高温变形流动应力模型研究[J].金属学报, 2007, 43(9): 937-942.

LI Miao-quan, YAO Xiao-yan, LUO Jiao, LIN Ying-ying, SUN Shao-bo, WANG Hai-rong. Study of flow stress model of the nickel-based superalloy GH4169 at high temperature deformation[J]. Acta Metallurgica Sinica, 2007, 43(9): 937-942.

[14] SELLARS C M, MCTEGART W J. On the mechanism of hot deformation[J]. Acta Metall, 1966, 14(3): 1136-1138.

[15] ZENER C, HOLLOMON H. Effect of strain rate upon plastic flow of steel[J]. Journal of Applied Physics, 1944, 15(1): 22-32.

[16] LIN Y C, CHEN M S, ZHONG J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel[J]. Computational Materials Science, 2008, 42(3): 470-477.

[17] MANDAL S, RAKESH V, SIVAPRASAD P V, VENUGOPAL S, KSIVISWANATHAN K V. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel[J]. Materials Science and Engineering A, 2009, 500(1/2): 114-121.

[18] SUN C Y, LIU J R, LI R, ZHANG Q D, DONG J X. Constitutive relationship of IN690 superalloy by using uniaxial compression tests[J]. Rare Metals, 2011, 30(1): 81-86.

[19] 孙朝阳, 刘金荣, 李 瑞, 张清东. Incoloy 800H高温变形流动应力预测模型[J]. 金属学报, 2011, 47(2): 191-196.

SUN Chaoyang, LIU Jinrong, ZHANG Qingdong. Constitutive modeling for elevated temperature flow behavior of Incoloy 800H superalloy[J]. Acta Metallurgica Sinica, 2011, 47(2): 191-196.

[20] LEI T, BAEDER J D. Uniformly accurate finite difference schemes forp-refinement[J]. SIAM Journal on Scientific Computing, 1999, 20(3): 1115-1131.

[21] PHANIRAJ M P, LAHIRI A K. The applicability of neural network model to predict flow stress for carbon steels[J]. Journal of Materials Processing Technology, 2003, 141(2): 219-227.

(编辑  王  超)

收稿日期：2014-03-13；修订日期：2014-10-17

通信作者：曲凤盛，副研究员；电话：18696586956；E-mail: qufengsheng@163.com