DOI:10.19476/j.ysxb.1004.0609.2018.09.04
5083铝合金热压缩应力-应变曲线修正与热加工图
高文理,关宇飞
(湖南大学 材料科学与工程学院,长沙 410082)
摘 要:在Gleeble-3500热模拟试验机上对圆柱体5083铝合金试样进行温度为300~500 ℃、应变速率为0.001~1 s-1条件下的热压缩试验。对实验获得的真应力应变曲线进行摩擦修正,依据摩擦修正后的应力应变曲线计算本构方程,采用包含Zener-Hollomon参数的本构方程描述摩擦修正后的5083铝合金流变应力行为,其热变形激活能为164.17 kJ/mol。根据摩擦修正后的真应力-应变曲线绘制热加工图,随着真应变的增加,失稳区域向着高应变速率、高变形温度区域扩展,5083铝合金适宜热变形工艺参数:变形温度为400~500 ℃、变形速率为0.01~0.1 s-1与340~450 ℃、变形速率为0.001~0.01 s-1。随着变形温度升高与应变速率降低,晶粒内位错密度减少,主要软化机制逐渐由动态回复转变为动态再结晶。
关键词:5083铝合金;应力-应变曲线修正;本构方程;热加工图;显微组织演变
文章编号:1004-0609(2018)-09-1737-09 中图分类号:TG146.2 文献标志码:A
5xxx系铝镁系列合金因较好的力学性能,如机械加工性以及优秀的耐腐蚀性,被广泛应用于造船业、管道、模具制造等行业[1]。在铝合金的加工制造过程中,有限元模拟技术与加工图的应用为工艺参数的设定提供了可靠的指导,在有限元模拟技术与加工图理论愈加广泛应用的背景下,通过实验获取精确应力应变曲线进而获得精确的数学模型与加工图成为应用成功的关键[2]。而金属材料在高温变形时的流变应力受到变形温度、变形程度、变形速率以及摩擦力、温升效应等因素影响,为获得真实反映变形温度、变形速度与变形程度对流变应力的影响,就需要排除摩擦力、变形热对流变应力的影响,因此,需要对获得的实验数据进行一定程度的修正。在工业历史中应用已久的5083铝合金,在热变形(0.01~10 s-1)条件下的流变应力行为已有文献阐述[3-4],近期包括考虑了温升效应对流变应力影响进行温升修正的流变应力关系研究[5],该研究表明在高应变速率下温升效应对流变应力曲线有更大影响,有关其他牌号的铝合金对金高温流变应力曲线的摩擦修正研究也有不少阐述[6-7],摩擦力对不同温度与应变速率下的流变应力均有影响,对摩擦力的影响进行修正十分必要。对于5083铝合金,包含了摩擦修正的应力应变关系的热加工图却鲜有报道。
因此,本文作者以铸态5083铝合金为研究对象,采用Gleeble-3500动态热模拟设备进行高温等温压缩实验,并对获得的真应力应变数据进行摩擦修正,构建精度较高的本构方程与基于动态材料模型(Dynamic material model,DMM )的加工图,以期为工业生产提供更可靠精确的参考工具。
1 实验
实验采用的原材料为工业生产的铸态5083坯料,其形态为d 400 mm×4000 mm圆柱体,铸锭经465 ℃、24 h[8]均匀化处理后,机加工为d 10 mm×15 mm的小圆柱体,为减小压缩实验过程中设备与试样间摩擦力对流变应力的影响,在试样两端预留槽内加入石墨片。试样在GleeBle-3500热模拟试验机上进行等温压缩实验,试样升温速率为10 ℃/s,并保温3 min,圧缩温度分别取300、320、340、360、460、480、500 ℃,应变速率分别为0.001、0.01、0.1、1 s-1,工程应变为0.7,即真应变为1.2,实验中由计算机自动收集数据并绘制真应力-真应变曲线。
2 结果与分析
2.1 流变应力行为
图1所示为5083铝合金高温压缩变形的真应力-真应变曲线。由图1可见,热变形初期随着变形程度的增大流变应力迅速上升,在达到峰值后逐渐趋于平缓直至实验结束。部分曲线出现锯齿状的波纹,这是由于在该条件下发生了不连续动态再结晶[9]。而试样与压头之间存在的摩擦力导致流变应力升高使得应力应变曲线末端呈现上翘的趋势[10]。在图1(b)中,相同温度下,随着应变速率的降低流变应力降低十分明显,故5083铝合金为典型的应变速率敏感材料。
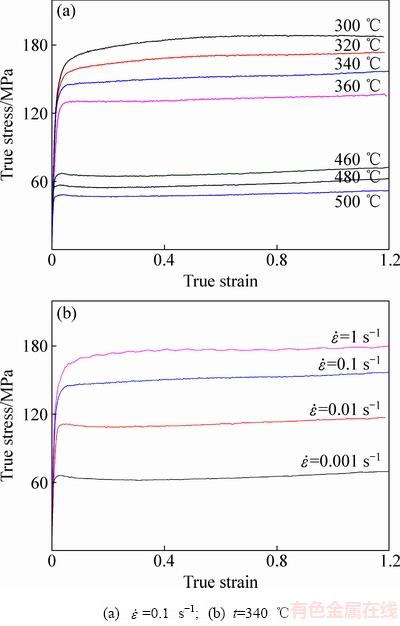
图1 不同变形条件下5083铝合金的真应力-真应变曲线
Fig. 1 True stress-true strain curves of 5083 aluminum alloy under different deformation conditions
2.2 摩擦力对流变应力的影响
在压缩过程中,试样与设备之间的摩擦力会阻碍试样两端的金属向外侧流动,从而改变了试样中的应力状况,使得压缩过程中试样中的应力一直处于偏高的状态,因此,需要进行修正。对压缩过程中摩擦影响的修正可由下列方程式求解[11]:
 (1)
(1)
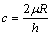 (2)
(2)
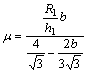 (3)
(3)
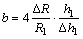 (4)
(4)
式中:pa为修正后的流动应力;pb为修正前的流动应力;R为试样的瞬时半径,由 确定(其中R0为试样的原始半径,h为试样的瞬时高度,h0为试样的原始高度);μ为摩擦因子;R1为变形后试样的平均半径,由
确定(其中R0为试样的原始半径,h为试样的瞬时高度,h0为试样的原始高度);μ为摩擦因子;R1为变形后试样的平均半径,由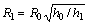 确定(其中h1为变形后试样的高度);Δh1为压缩的变形量,即Δh1=h0-h1,ΔR为最大鼓肚半径RM与压缩后压头与试样接触的底面半径RT的差值,RM与RT可以直接在多个试样上测量并取平均值获得。
确定(其中h1为变形后试样的高度);Δh1为压缩的变形量,即Δh1=h0-h1,ΔR为最大鼓肚半径RM与压缩后压头与试样接触的底面半径RT的差值,RM与RT可以直接在多个试样上测量并取平均值获得。
由式(1)~(4)只需测得压缩后试样高度以及鼓肚大小即可计算得出应变修正量。式(1)~(4)是由EBRAHIMI等[12]提出的考虑了应变速率、变形温度、材料特性、微观结构、变形历史等一系列因素化简得出的公式,该文献经过对比无润滑条件、云母粉润滑条件以及玻璃润滑剂润滑条件下,应用式(1)~(4)对测得应力应变曲线进行修正,其结果表明:不同润滑条件下测得的初始应力应变曲线不同,但是利用式(1)~(4)修正后的应力应变曲线间差异可忽略不计。故本研究结果在试验阶段添加石墨润滑并不会影响修正结果。
由图2可见,经摩擦修正后的应力应变曲线普遍低于原始应力应变曲线,修正后的流变应力在变形初期与原始流变应力之间的差值较小,并随着应变的增大逐渐增大,在实验结束即真应变为1.2时达到最大差值。这是由于试样在压缩过程中,试样两端与压头和底座之间的接触面积逐渐增大,摩擦力随之逐渐增大,摩擦力对流变应力的影响逐渐增大并在最大应变时达到最大影响。亦可由图2得出,摩擦在不同变形温度与变形速率下对应力的影响是不同的,总体表现为温度越低、应变速率越高,影响越大,温度的升高使材料强度降低从而降低了摩擦力的影响。
2.3 本构方程的建立
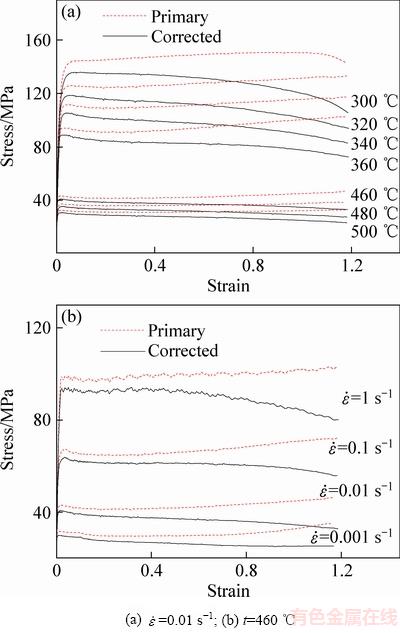
图2 5083铝合金修正前后的流动应力曲线
Fig. 2 Flow stress curves for aluminum alloy 5083 before and after correction at different deformation conditions
材料的本构关系依据应力水平的不同,对应着3个不同的方程[12]:
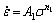 (5)
(5)
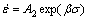 (6)
(6)
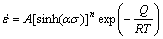 (7)
(7)
式中: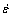 为应变速率;σ为真应力(本研究中取峰值应力);β为图3(b)中曲线的斜率;Q为变形激活能,A1、A2、A为材料常数;R是气体常数;T为变形温度;n1、n则为硬化指数。式(5)适用于低应力水平,即ασ≤0.8;式(6)适用于高应力水平,即ασ≥1.2;式(7)则可用于所有应力水平,可以较好地描述变形过程,其中
为应变速率;σ为真应力(本研究中取峰值应力);β为图3(b)中曲线的斜率;Q为变形激活能,A1、A2、A为材料常数;R是气体常数;T为变形温度;n1、n则为硬化指数。式(5)适用于低应力水平,即ασ≤0.8;式(6)适用于高应力水平,即ασ≥1.2;式(7)则可用于所有应力水平,可以较好地描述变形过程,其中 。应变速率和T的关系则可用Zener-Hollomon参数表示:
。应变速率和T的关系则可用Zener-Hollomon参数表示:
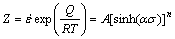 (8)
(8)
参数Z的物理意义为温度补偿的应变速率因子。获得摩擦修正后的不同温度与应变下的5083铝合金应力值(即应力峰值),带入式(5)~(8)可拟合出铸态5083铝合金的本构方程。
设在一定温度下变形激活能Q是常数,在低应力下,即选取高温度段460、480、500 ℃对应应力值,对方程(5)两边取对数,变形为
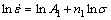 (9)
(9)
在高应力下,即选取低温度段300、320、340、360 ℃应力值,对方程(6)取对数,变形为
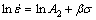 (10)
(10)
分别以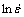 与lnσ以及
与lnσ以及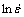 与σ作为坐标轴作图,如图3所示。利用最小二乘法线性回归拟合斜线后,求得各斜线斜率,并取平均值,图3(a)中斜率平均值设为n1,图3(b)中斜率平均值设为β,得n1=5.483,β=0.0669。故求得α=β/n1=0.0122。对式(7)两边取对数,可以获得变形激活能Q的求解方程:
与σ作为坐标轴作图,如图3所示。利用最小二乘法线性回归拟合斜线后,求得各斜线斜率,并取平均值,图3(a)中斜率平均值设为n1,图3(b)中斜率平均值设为β,得n1=5.483,β=0.0669。故求得α=β/n1=0.0122。对式(7)两边取对数,可以获得变形激活能Q的求解方程:
 (11)
(11)
式中:n为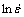 与lnsinh(ασ)线性关系的斜率平均值,K为lnsinh(ασ)与1000/T斜率平均值,R为气体摩尔常数,进而以
与lnsinh(ασ)线性关系的斜率平均值,K为lnsinh(ασ)与1000/T斜率平均值,R为气体摩尔常数,进而以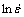 与lnsinh(ασ)、lnsinh(ασ)与1000/T分别为X、Y轴绘制曲线图,如图3(c)和(d)所示。
与lnsinh(ασ)、lnsinh(ασ)与1000/T分别为X、Y轴绘制曲线图,如图3(c)和(d)所示。
由图3(c)求得各斜线的斜率平均值,得n=4.75;由图3(d)求得各斜线斜率平均值,得K=4.157,所以铸态5083铝合金变形激活能Q=RnK=164.17kJ/mol。对式(8)两边取对数,并带入T与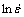 可求得不同温度与应变速率对应的lnZ值,进而绘制lnZ-lnsinh(ασ)曲线图,如图3(e)所示。由一元线性回归分析,得到lnZ与lnsinh(ασ)关系:
可求得不同温度与应变速率对应的lnZ值,进而绘制lnZ-lnsinh(ασ)曲线图,如图3(e)所示。由一元线性回归分析,得到lnZ与lnsinh(ασ)关系:
lnZ=23.362+4.27lnsinh(ασ) (12)
可知材料常数A=1.40×1010,综上所述可以得到,铸态5083铝合金热变形流变学应力方程:
 (13)
(13)
采用含Z参数的方程可表示为
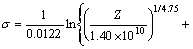
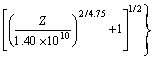 (14)
(14)
2.4 热加工图的建立
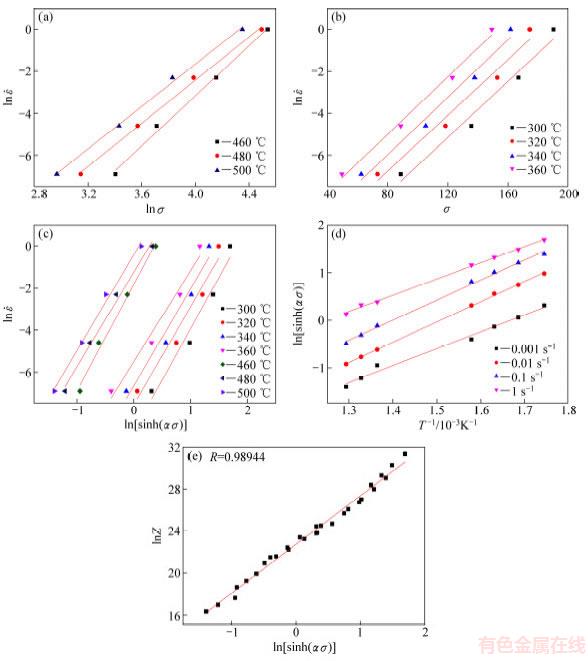
图3 5083铝合金摩擦修正后本构方程计算过程
Fig. 3 Calculation process of constitutive equation after friction correction of 5083 aluminum alloy
热加工图主要基于动态材料模型理论,由能量耗散图和失稳图叠加而成。材料在热加工过程中,可认为总能量的耗散主要用于材料的塑性变形和材料显微组织变化两个方面,而功率耗散图则是在应变速率和变形温度所构成的二维平面绘制出用于显微组织变化所耗散能量与线性耗散能量的比例关系的等值线。而在应变速率与变形温度构成的二维平面内绘出失稳判据等值线就构成了失稳图。构建热加工图可依据以下两个方程构建[14]:
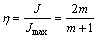 (15)
(15)
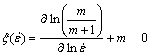 (16)
(16)
式中:η为功率耗散因子;m为应变速率敏感性指数,
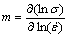 (17)
(17)
选取经摩擦修正的数据,用3次样条插值法对数据进行扩充,分别绘制出真应变为0.4、0.8、1.2时的功率耗散图与失稳图,并叠加生成相应的热加工图。
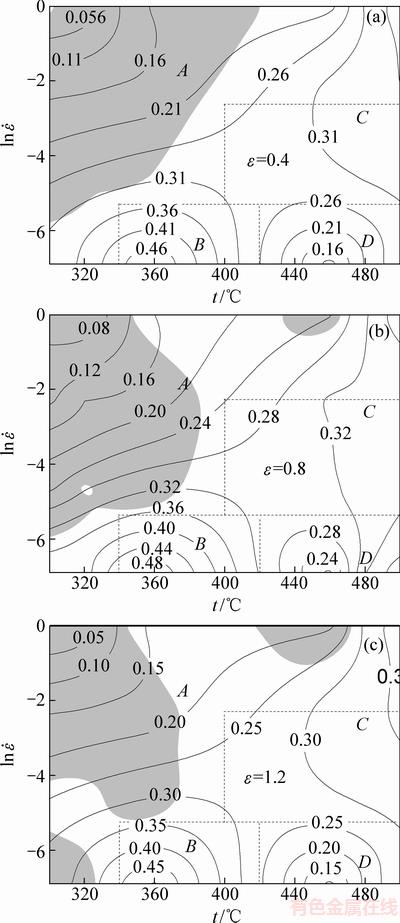
图4 不同真应变下5083铝合金的加工图
Fig. 4 Processing maps of 5083 Al alloy at different true strains
图4所示为5083铝合金分别在真应变为0.4、0.8、1.2时的加工图,阴影部分为失稳区域,随着变形量的增加,功率耗散因子变化并不大,而失稳区域逐渐出现在高温高应变速率区域与低变形温度区域,失稳区主要集中在加工图的左侧,这与WANG等[15]指出变形程度对失稳区有显著影响的结论相一致。以应变为1.2时的加工图为例,功率耗散因子在变形温度360 ℃,应变速率0.001 s-1时达到峰值0.49,在变形温度360 ℃至455 ℃之间功率耗散因子呈现下降趋势,大于455 ℃又开始上升。应变速率0.007 s-1与0.2 s-1之间时功率耗散因子表现较为平滑,其值为25%~35%。功率耗散因子等值线在变形温度为450 ℃附近以及应变速率0.01 s-1以下出现较大弯折,这种弯折一般是发生了相变[16],即β相(Mg2Al3)从基体α(Al)相中析出。加工图可以依据失稳区域与功率耗散率分为图5中A、B、C、D等4个区域。在温度大于400 ℃应变速率在0.005~0.1 s-1的范围即C区域内功率耗散因子较大也非常稳定,约为30%,是适宜变形的区域;而D区,即变形温度为420~500 ℃,应变速率为0.001~0.01 s-1的区域,虽然没有出现失稳区域,但是功率耗散因子随着应变速率的减小急剧降低,组织演变耗散能占比过低,并不推荐在此区域进行变形;B区域即变形温度为340~420 ℃、应变速率为1×10-3~1×10-2 s-1,功率耗散因子普遍较高,等值线也比较平滑,且不存在失稳区域,该区域的应变速率较小,满足低应变速率条件的情况下可以在此区域变形;A区域大面积均为加工失稳区域,热变形时应当避开。仅靠加工图判定适宜变形区域并不准确,还需要金相观察来佐证加工图的可靠性,将在后节详细阐述。
2.5 软化机制与显微组织演变
为判定5083铝合金DRX软化临界条件,引用 BAMBACH[17]提到的加工硬化率的方法研究DRX软化行为的临界条件。这里采用其中POLIAK等[18]提出的Poliak-Jonas准则:材料DRX软化临界条件为 。即θ-σ曲线的拐点(加工硬化率
。即θ-σ曲线的拐点(加工硬化率 )。以变形条件为480 ℃、0.1 s-1时为例,绘制θ-σ曲线如图5所示。由图5可知,在该变形条件下,发生动态再结晶软化的临界应力σc为43.38 MPa,峰值应力σp为54.29 MPa。
)。以变形条件为480 ℃、0.1 s-1时为例,绘制θ-σ曲线如图5所示。由图5可知,在该变形条件下,发生动态再结晶软化的临界应力σc为43.38 MPa,峰值应力σp为54.29 MPa。
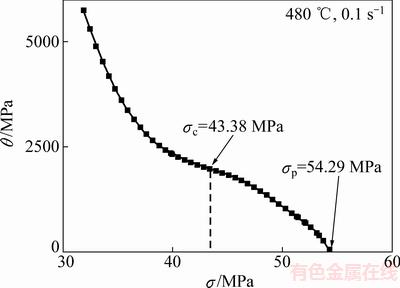
图5 5083铝合金θ-σ曲线
Fig. 5 θ-σ curve of 5083 aluminum alloy (480 ℃, 0.1 s-1)
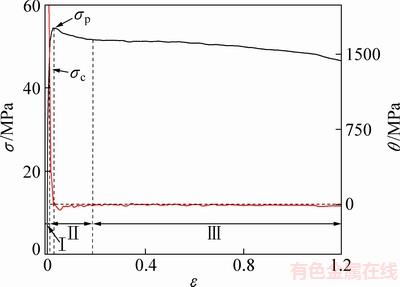
图6 5083铝合金θ-ε曲线(480 ℃,0.1 s-1)
Fig. 6 θ-ε curves of 5083 aluminum alloy (480 ℃, 0.1 s-1)
在480 ℃、0.1 s-1条件下,5083铝合金的流变应力曲线呈现典型的DRX软化特征,如图6所示,Ⅰ阶段中,流变应力σ随着应变ε的增加而迅速增大,此时对应的加工硬化率为正值且急剧减小,这一阶段的变形加工硬化占据主导作用;Ⅱ阶段中,流变应力σ达到DRX软化临界应力σc,加工硬化率θ由正值降为负值并停止降低转而向θ=0趋近,且其与X轴交点对应着峰值应力σp,这一阶段为DRX软化区;Ⅲ阶段中,θ几乎为0,这一阶段软化作用与加工硬化相平衡,流变应力表现为稳态流变。
图7所示为加工图A、B、C、D区域内试样变形终了时金相照片。如图7(a)所示,该试样位于区域A,由于此区域应变速率较大,大部分区域温度较低,动态软化在与加工硬化竞争中处于劣势,使得部分晶粒可以完成变形而部分晶粒产生与压缩轴成一定角度的剪切变形带。图7(b)中B区域应变速率普遍较低,变形温度不高但是功率耗散因子却较高,使得有足够的能量驱动动态回复与动态再结晶的发生,在图7(b)中还可以看到沿着晶界存在着许多再结晶晶粒,部分再结晶晶粒已经被沿径向拉长,呈现纤维组织特征,此区域获得的晶粒也较均匀,动态再结晶进行程度较高,且此区域功率耗散因子较大,是适合变形的区域。图7(c)中C区域功率耗散因子较B区域小,但更为平稳,应变速率较低但变形温度较高,依然有足够的驱动力促使动态回复与动态再结晶的发生;沿晶界有许多再结晶晶粒,晶粒尺寸并不均匀,有被沿径向拉长的大晶粒存在,但是并未出现加工失稳现象,此区域可以在较高的变形速率且合适的温度下进行热变形,综合工业生产成本考虑,在此区域选取加工参数为宜。图7(d)中D区域位于高变形温度低应变速率下,可以观察到大量长大的再结晶晶粒,但这一区域的功率耗散因子较小而且变化很大,并非最佳的变形区域。金相观察结果符合加工图规律,与LIU等[19]指出的一般情况下失稳区出现剪切断裂带、孪晶与微裂纹,稳定变形区出现再结晶晶粒相一致。

图7 5083铝合金在不同变形条件下的金相显微组织
Fig. 7 Optical deformed microstructures of 5083 aluminum alloy under different conditions

图8 5083铝合金在不同变形条件下的TEM像
Fig. 8 TEM images of 5083 aluminum alloy under different conditions
图8所示为5083铝合金在不同变形条件下的透射电镜照片。由图8(a)可见,在低变形温度(340 ℃)与高应变速率(0.1 s-1)下,出现大量纵横交错的位错,大量位错被分散的第二相粒子钉扎,且没有足够的能量进行滑移和攀移,动态回复程度十分有限,宏观表现为严重的加工硬化现象,使得应力水平较高。随着应变速率从0.1 s-1降低至0.001 s-1,如图8(b)所示,应变速率较低,位错有较宽裕的时间通过滑移与攀移的方式湮灭与重组,出现将晶粒分割为亚晶粒的位错墙,部分亚晶已经有所长大,这表明应变速率的降低加强了动态软化,动态回复程度增加但仍然有限,故此时主要软化机制依旧为动态回复。当变形温度增加为480 ℃,应变速率为0.1 s-1时,如图8(c)所示,原子热激活能增强,位错的活动能力增强,拥有足够的驱动力迁移并脱离位错网使得亚晶粒逐渐合并,形成大量等轴小晶粒,且晶粒内位错密度明显降低,位错的湮灭使得动态再结晶比较完全,故此时主要的软化机制为动态再结晶[20]。在温度为480 ℃变形速率为0.001 s-1时,如图8(d)所示,随着应变速率的降低,动态再结晶的晶粒有充足的时间长大,小角度晶界演变为大角度晶界,晶粒内几乎没有位错,仅有部分第二相粒子分布。综上所述,随着变形温度的升高与应变速率的降低,位错逐渐获得能量进行滑移与攀移,并形成小角度晶界的亚晶粒,此时主要软化机制为动态回复;当驱动力达到一定临界值时,位错进一步湮灭,小角度晶界演变为大角度晶界,发生了动态再结晶,主要软化机制也逐渐由动态回复演变为动态回复与动态再结晶共存,最后发展为动态再结晶为主要软化机制。宏观表现为随着变形温度的升高与应变速率的降低,流变应力降低。而结合加工图与金相观察,在B区域与C区域均有有利于热变形的动态再结晶晶粒的出现,B区与C区尽管再结晶尚未完全,但是所处区域功率耗散因子较高,即在此区域材料显微组织耗散引起的熵增加的变化率最大,最有利于体系从塑性变形向稳态变形发展[21],故此区域为最佳变形区域。
3 结论
1) 摩擦力对流变应力的影响在各温度与各应变速率下均较明显,并随着真应变的增大而增大。
2) 获得经过摩擦修正的真应力应变曲线,采用包含热激活能Q的双曲正弦模型描述5083铝合金热压缩时的流变行为,其α值0.0122,n值为4.75,求得其热激活能为164.17 kJ/mol。
3) 利用摩擦修正与温升修正后的真应力应变曲线建立5083铝合金的热加工图,得出5083铝合金的适宜热变形工艺参数:变形温度400~500 ℃,应变速率0.01~0.1 s-1或变形温度340~450 ℃,应变速率0.001~0.01 s-1。
4) 随着变形温度的升高与变形速率的降低,位错密度降低,出现亚晶粒并逐渐长大,主要软化机制由动态回复转变为动态再结晶。
REFERENCES
[1] 王祝堂. 铝合金及其加工手册[M]. 长沙: 中南工业大学出版社, 2000.
WANG Zhu-tang. Aluminum alloy and its processing manual[M]. Changsha: Central South University of Technology Press, 2000.
[2] 郭海廷. 基于热加工图理论的铝合金6061锻造工艺优化研 究[D]. 武汉: 华中科技大学, 2012.
GUO Hai-ting. Study on optimization of forging process of aluminum alloy 6061 based on thermal processing diagram theory[D]. Wuhan: Huazhong University of Science and Technology, 2012.
[3] 梁奕清, 方 刚. 5083和7020变形铝合金加工图的研究[J]. 材料研究与应用, 2011, 5(3): 218-220.
LIANG Yi-qing, FANG Gang. Study on machining drawings of 5083 and 7020 deformed aluminum alloys[J]. Materials Research and Application, 2011, 5(3): 218-220.
[4] 徐清波, 陶友瑞, 米 芳. 5083铝合金高温流变本构关系研 究[J]. 矿冶工程, 2013, 33(5): 124-126.
XU Qing-bo, TAO You-rui, MI Fang. Study on constitutive relation of high temperature rheology of 5083 aluminum alloy[J]. Mining and Metallurgy Engineering, 2013, 33(5): 124-126.
[5] 吴文祥, 孙德勤, 曹春艳, 王战锋, 张 辉. 5083铝合金热压缩变形流变应力行为[J]. 中国有色金属学报, 2007, 17(10): 1667-1671.
WU Wen-xiang, SUN De-le, CAO Chun-yan, WANG Zhan-feng, ZHANG Hui. Flow stress behavior of 5083 aluminium alloy under hot compression deformation[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(10): 1667-1671.
[6] 刘大博, 杨守杰, 王克鲁, 董显娟. 2D70铝合金热变形行为及加工图[J]. 中国有色金属学报, 2013, 23(8): 2077-2082.
LIU Da-bo, YANG Shou-jie, WANG Ke-lu, DONG Xian-juan. Hot deformation behavior and processing map of aluminum alloy 2D70[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(8): 2077-2082.
[7] 张伟红, 张士宏. NiTi合金热压缩实验数据的修正及其本构方程[J]. 金属学报, 2006, 42(10): 1036-1040.
ZHANG Wei-hong, ZHANG Shi-hong. Modification of NiTi alloy hot compression experiment data and its constitutive equation[J]. Acta Metallurgica Sinica, 2006, 42(10): 1036-1040.
[8] 马成国, 桑玉博. 5083铝合金均匀化退火工艺研究[J]. 热加工工艺, 2012, 41(24): 205-207.
MA Cheng-guo, SANG Yu-bo. Study on homogenizing annealing process of 5083 aluminum alloy[J]. Thermal Processing Technology, 2012, 41(24): 205-207.
[9] BLUM W, ZHU Q, MERKEL R, MCQUEEN H J. Geometric dynamic recrystallization in hot torsion of Al5Mg0.6Mn (AA5083)[J]. Materials Science & Engineering A, 1996, 205(205): 23-30.
[10] 仇琍丽, 高文理, 陆 政, 冯朝辉. 7A85铝合金的热压缩流变行为与显微组织[J]. 材料工程, 2016, 44(1): 33-39.
QIU Li-li, GAO Wen-li, LU Zheng, FENG Zhao-hui. Thermo-compression rheological behavior and microstructure of 7A85 aluminum alloy[J]. Materials Engineering, 2016, 44 (1): 33-39.
[11] MALLOL J, SARRAGA MC, BARTOLOME M. Hot working behavior of near-α alloy IMI834[J]. Materials Science & Engineering A, 2005, 396(1/2): 50-60.
[12] EBRAHIMI R, NAJAFIZADEH A. A new method for evaluation of friction in bulk metal forming[J]. Journal of Materials Processing Tech, 2004, 152(2): 136-143.
[13] 杨胜利, 沈 健, 闫晓东, 李锡武, 孙宝庆. Al-Cu-Li-Mg- Mn-Zn-Ag合金的热变形流变行为与本构方程[J]. 中国有色金属学报, 2015, 25(8): 2083-2090.
YANG Sheng-li, SHEN Jian, YAN Xiao-dong, LI Xi-wu, SUN Bao-qing. Flow behavior and constitutive equations of Al-Cu-Li-Mg-Mn-Zn-Ag alloy during isothermal compression[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(8): 2083-2090.
[14] 冯 江,田保红, 孙永伟, 刘 勇, 张 毅, 任凤章. Al2O3/Cu-WC复合材料热变形行为及热加工图[J]. 中国有色金属学报, 2012, 22(12): 3462-3467.
FENG Jiang, TIAN Bao-hong, SUN Yong-wei, LIU Yong, ZHANG Yi, REN Fen-zhang. Hot deformation behavior and processing maps of Al2O3/Cu-WC composites[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(12): 3462-3467.
[15] WANG Y, PAN Q, SONG Y, LI C, LI Z. Hot deformation and processing maps of X-750 nickel-based superalloy[J]. Materials & Design, 2013, 51(5): 154-160.
[16] 周 军, 曾卫东, 舒 滢. 应用热加工图研究TC17合金片状组织球化规律[J]. 稀有金属材料与工程, 2006, 35(2): 265-269.
ZHOU Jun, ZENG Wei-dong, SHU Ying. Study on spheroidization rule of TC17 alloy flake by hot work drawing[J]. Rare Metal Materials and Engineering, 2006, 35(2): 265-269.
[17] BAMBACH M. Implications from the Poliak–Jonas criterion for the construction of flow stress models incorporating dynamic recrystallization[J]. Acta Materialia, 2013, 61(16): 6222-6233.
[18] POLIAK E I, JONAS J J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization[J]. Acta Materialia, 1996, 44(1): 127-136.
[19] LIU Y, HU R, LI J, KOU H, LI H. Characterization of hot deformation behavior of Haynes230 by using processing maps[J]. Journal of Materials Processing Tech, 2009, 209(8): 4020-4026.
[20] LI B, PAN Q, YIN Z. Microstructural evolution and constitutive relationship of Al-Zn-Mg alloy containing small amount of Sc and Zr during hot deformation based on Arrhenius-type and artificial neural network models[J]. Journal of Alloys & Compounds, 2014, 584(1): 406-416.
[21] 陈 前, 王 岩. δ相时效态GH4169合金的热加工行为[J]. 中国有色金属学报, 2015, 25(10): 2727-2737.
CHEN Qian, WANG Yan. Hot working behavior of delta-processed GH4169 alloy[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(10): 2727-2737.
Correction of flow stress-strain curve and processing maps of 5083 aluminum alloy during hot compression
GAO Wen-li, GUAN Yu-fei
(School of Materials Science and Engineering, Hunan University, Changsha 410082, China)
Abstract: The hot compression tests of the cylindrical 5083 aluminum alloy sample were carried out on Gleeble-3500 thermal simulator at the temperature range of 300-500 ℃ and the strain rate range of 0.001 s-1. The real stress and strain curves obtained by the experiment were subjected to friction correction. The constitutive equation of Zener-Hollomon parameters was used to describe the flow behavior of 5083 aluminum alloy after friction correction and activation energy of the thermal deformation is 164.17 kJ/mol. According to the friction correction of the true stress-strain curve drawing the processing map, finding that the unstable region expands toward high strain rate and high deformation temperature with the increase of true strain. The suitable thermal deformation process parameters of 5083 aluminum alloy are as follows: deformation temperatures of 400-500 ℃ at deformation rates of 0.01-0.1 s-1 and deformation temperatures of 340-450 ℃ at deformation rates of 0.001-0.01 s-1.With the increases of deformation temperature and strain rate, the dislocation density within the grain decreases, and the main softening mechanism gradually changes from dynamic recovery to dynamic recrystallization.
Key words: 5083 aluminum alloy; stress-strain curve correction; constitutive equation; processing map; microstructural evolution
Foundation item: Projects(51474101, 51271076, 51474195) supported by the Natural Science Foundation of China
Received date: 2017-07-24; Accepted date: 2018-01-24
Corresponding author: GAO Wen-li; Tel: +86-13873110708; E-mail: wenligaohd@163.com
(编辑 李艳红)
基金项目:国家自然科学基金资助项目(51474101,51271076,51474195)
收稿日期:2017-07-24;修订日期:2018-01-24
通信作者:高文理,教授,博士;电话:13873110708;E-mail:wenligaohd@163.com