J. Cent. South Univ. (2016) 23: 2951-2957

DOI: 10.1007/s11771-016-3359-7

Characteristics and mechanisms of strain waves generated in rock by cylindrical explosive charges

LIU Ke-wei(刘科伟)^{1, 2, 3}, LI Xiao-han(李萧翰)^{1, 3}, LI Xi-bing(李夕兵)^{1, 3}, YAO Zhi-hua(姚志华)²,

SHU Zong-xian(舒宗宪)², YUAN Ming-hua(袁明华)²

1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. Yuxi Mining Co. Ltd., Yunnan Copper Industry (Group), Yuxi 653100, China;

3. Hunan Key Laboratory of Resources Exploitation and Hazard Control for Deep Metal Mines,Central South University, Changsha 410083, China

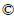Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: A superposing principle, by suitably adding the strain waves from a number of concentrated explosive charges to approximate the waves generated by a cylindrical charge based on the strain wave of a point or small spherical explosive charge generated in rock, is used to further study the triggering time of strain gauges installed in radial direction at same distances but different positions surrounding a cylindrical explosive charge in rock. The duration of the first compression phase and peak value of strain wave, and furthermore, their differences are analyzed and some explanations are given. Besides that, the gauge orientation in which the maximum peak value occurs is also discussed. At last, the effect of velocity of detonation (V.O.D.) of a cylindrical explosive charge on the strain waves generated in the surrounding rock is taken as key research and the pattern of peak amplitude of a strain wave varies with the V.O.D. is likely to have been found.

Key words: cylindrical explosive charge; strain wave; concentrated explosive charge; elemental strain wave; superposing principle; velocity of detonation (V.O.D.); velocity of propagation (V.O.P.)

1 Introduction

In rock mass blasting of high energy explosive operations, rock breaking is treated as the result of the strain wave generated in the rock [1-3]. If the strain pulse caused in this way travelling through the surrounding rock is sufficient to overcome the strength of the rock, then fracture will occur. In the zone immediately surrounding the cylindrical charge the compressive strains are large enough to cause cracking [4-7], but for the typical explosive charge used in Witwatersrand practice [8] this zone is limited only to a cross-sectional with radius of about 15.34 cm; therefore, the normally broken is required to further explain when other larger burdens are adopted. However, although strain wave generated by a cylindrical explosive charge plays considerably important part in rock blasting and is of profound research and application value [9-10], only a few explicit mathematical solutions for linear source problems have been derived from elastic wave theory. Researchers have presented a number of solutions for the wave form produced in an elastic solid by a spherical explosive source. SELBERG [11] first proposed a solution for the compression wave generated by an infinitely long cylindrical charge; HEELAN [12] made a further study and derived expressions for both the compression and shear waves generated by a charge of limited length.

All these solutions above assumed that the explosive pressure to be applied to the surrounding rock simultaneously along the entire length of the charge, which means the explosive charge is detonated instantaneously with an infinitely high detonation velocity, but apparently it doesn’t always agree with practice. For example, BLAIR [13] made a numerical comparison between the Heelan’s approximation and an exact solution for the radiation of seismic waves produced by a short cylindrical charge, and concluded that the Heelan’s solution significantly overestimates the true seismic motion in some cases. JORDAN [14] considered the fact of a finite detonation velocity in the explosive, and deduced a solution applicable to a cylindrical explosive charge restricted to the cases at a velocity of detonation (V.O.D.) much greater than the velocity of propagation (V.O.P.) through the surrounding rock.

Since in most of the rock mass blasting practical cases, the V.O.D. is approximately equal to or less than the longitudinal propagation velocity, an solution based on this condition can be used to precisely and practically explain the characteristics of strain wave in rock for almost all the rock breaking explosives. In order to understand the effect of V.O.D. on the strain wave in the surrounding rock and furthermore the mechanism of strain wave in actual rock breaking, intensive study on this kind of solution is necessary. PLEWMAN and STARFIELD [15] proposed a solution by suitably superposing the waves from a number of concentrated explosive charges to approximate the wave generated by a cylindrical charge based on the strain wave form expression of a point or small spherical explosive charge generated in rock. WHITE and SENGBUSH [16] used the same superposing method and made some success with Heelan’s test data, and it has shown that this method gave results consistent with observed phenomena [17].

On the basis of previous research results, this work uses the above superposing principle to further study the triggering time of strain gauges installed in radial direction at same distances but different positions surrounding a cylindrical explosive charge in rock, the duration of the first compression phase and peak value of strain wave, and furthermore the differences of them are analyzed and some explanation are given. Besides that, the gauge orientation in which the peak value occurs is also discussed. At last, the effect of V.O.D. of a cylindrical explosive charge on the strain waves generated in the surrounding rock is taken as key research. The pattern of peak amplitude of a strain wave varies with the V.O.D. is likely to have been found which indicates the V.O.D. has a direct effect on strain wave and is of vital importance in rock breaking.

2 Superposition of strain wave

2.1 Strain waves generated by a point or small spherical explosive charge

When a point charge or small spherical explosive charge is detonated in rock which is assumed as a near- elastic than perfectly elastic medium, the strain wave at any point at a distance R from the charge can be described as

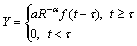                       (1)

where f(t) is a function of time known as function of wave shape, and aR^-α is the amplitude of strain wave at R and shows an attention of R^-α with distance from the charge. For a perfectly elastic medium, the attention is only caused by the expansion of the wave front with increasing R and the coefficient of attention α is equal to 1; while for a rock material, internal loss of energy contributes further attenuation, so in general α≥1. The time t in formula (1) is measured from the instant moment of detonation, and τ is the time taken for the first disturbance from the charge to point R which is called as travel time, i.e. τ=R/C, where C is the V.O.P. in rock. The strain Y at point R is a vector quantity in radial direction from the charge pointing at point R. It should be noted that for a dilatational wave, besides this radial component, a tangential strain component at right-angles to Y is accompanied. However, except at the immediate vicinity of the charge, it is much smaller and more rapidly attenuates. So, the effect of this strain component is ignored.

2.2 Strain waves generated by a cylindrical explosive charge

Compared to the point or small spherical explosive charge, the expression of strain wave generated in rock by a cylindrical explosive charge is more complicated. Now, consider the case of a cylindrical charge of length l detonated at point O with a V.O.D. V at time t=0. Setting up cylindrical coordinate system with origin O, axes Z along the cylindrical charge and R which is vertical as shown in Fig. 1. Then, a way is needed to be found to express the strain wave at any point P(r, z).

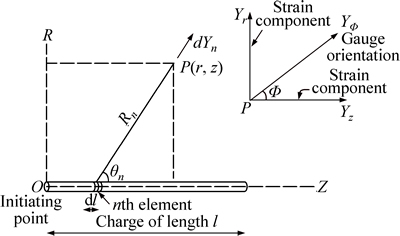
Fig. 1 Cylindrical coordinate system

First, divide the cylindrical charge of length l into N equal elements of length dl, each element is replaced by a concentrated charge at its center. Then, the cylindrical charge could be regarded as a number of concentrated charges detonated one after another with same time interval, and this time interval depends on the V.O.D. V. Now, according to formula (1), the elemental wave generated by the nth concentrated charge can be expressed as

               (2)

where τ_n is a combination of the time taken for detonation from origin O to the nth element and the travel time from the nth element to point P in rock:

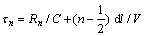                      (3)

As shown in Fig. 1, the distance R_n can be written as

                   (4)

If the angle between the strain dY_n and the axe Z is θ_n , then sinθ_n =r/R_n . Paralleling to the axes Z and R, the strain dY_n then can be resolved into components dY_ncosθ_n and dY_nsinθ_n, respectively.

Adding all the dY_ncosθ_n and dY_nsinθ_n components respectively, the components of the superposing strain wave of a cylindrical charge of length l at any point P is obtained as

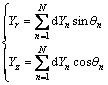                           (5)

When a unidirectional strain gauge is set at point P and oriented at an angle φ to the axis Z, the wave recorded should be

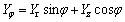                        (6)

As reviewed above, if the function of elemental wave shape is given, by writing a simple computer program using Eqs. (2)-(6), it is in a position to easily obtain the superposing strain wave which should be measured at a strain gauge at any point in the rock surrounding a cylindrical charge.

2.3 Function of elemental wave shape

For the function of the elemental wave shape, PLEWMAN and STARFIELD [15] suggested that a damped sine wave could give a good approximation superposition and the corresponding function of the elemental wave shape f(t) is

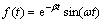                            (7)

where ω and β are the frequencies of the elemental wave and damping coefficient respectively, and both of them are constants.

Figrue 2 compares two elemental wave shapes of damping β=0.0015/μs and β=0.005/μs at the same frequency ω=0.01/μs. The elemental wave A shows being slightly damped while B shows being heavily damped. Both of them could be considered as the wave shapes produced by unknown explosive pressures p(t) and measured at the periphery of the blast hole which leads to superposing strain waves that would be measured at strain gauges in rock.

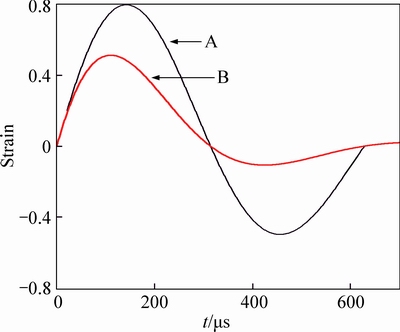
Fig. 2 Elemental strain waves with different damping coefficients

A large number of studies [18-23] have indicated that the strain wave shape and damping coefficient are concerned with the property of rock in which the blasting happens. Since the slightly damped elemental wave A in Fig. 2 can give a good approximation superposition to the wave shape measured in quartzite, in this work, with a great deal of reservation, this elemental wave will be taken as a basic damped sine wave to develop the following study. Besides that, if further use the attenuation coefficient α=1.2 deduced by SAFFY et al [24] which agrees with measured values, it is in a position to obtain the strain wave by superposing calculation for a variety of values of the length of charge, V.O.D., the position and orientation of the strain gauge.

2.4 Superposing of elemental waves

Figure 3 shows the progress of superposing the elemental waves. As shown in Fig. 3(a), a cylindrical charge of length 1 m (divided into 10 equal elements of length 0.1 m) is detonated from left end and successive elemental waves will arrive at point P(r=0, z=1.5) on axis Z. The strain wave is superposed by adding the elemental waves as shown in Fig. 3(b). The values for the V.O.D. and V.O.P. are 2590.8 m/s and 5334 m/s, respectively, corresponding to a gelignite charge detonated in quartzite. The scale on the strain axis is purely arbitrary and the amplitude of the unattenuated elemental wave is set to 1.0, i.e. a in Eq. (2) is equal to 1.0. As a matter of convenience, this scale will be used throughout this work. It should be noted that the point P is on axis Z which means all the elemental strains are in the direction of the axis Z, i.e. Y_r component is not available. Furthermore, the successive elemental waves arrive at the point P with the same time interval and each elemental wave travels a shorter distance and less attenuated.

Fig. 3 Superposing principle:

It should be noted here that in theory, for a linear or cylindrical charge, the accuracy of the results should increase as the length of an element dl approaches 0 or the cross-sectional diameter of the cylindrical charge, but in fact it is found that for a linear charge when the length dl decreases over a limit, no further significant contribution on the accuracy improvement will occur.

3 Gauge position and orientation

In the example of superposing the elemental waves as shown in Fig. 3, the existence of special geometry of the situation between the charge and point P (no Y_r component available) makes the strain wave and foregoing remarks untypical, generally, the interactions of the elemental waves vary significantly with the position and orientation of the strain gauge.

3.1 Effect of gauge position on strain wave

In order to study the effect of the gauge position on the strain wave measured at a strain gauge, assume that five measurement points are placed along a semi-circle of radius 1.5 m and each gauge is set and oriented in radial direction to the midpoint of the 1 m charge as shown in Fig. 4. According to the foregoing superposing principle with the same values for V and C as above, the strain waves should be recorded on five gauges which can be calculated and shown in Fig. 5. It can be seen from Fig. 5 that unlike the readings from a point or small spherical explosive charge, even at the same distance from the midpoint of the charge to the measurement points, the strain waves measured at five measurement points vary apparently.

Firstly, as shown in Fig. 5, each gauge is triggered at different time after the detonation. It can be seen from the progress of adding the elemental waves that this is obviously depending on the time (τ₁) taken for the first elemental wave from the midpoint of the first element charge to the measurement points. For all the five measurement points, τ₁=R₁/C+0.5dl/V, then only one element charge is detonated with same time 0.5dl/V taken for detonation, so, the order of triggering for the gauges now is up to the distance from the midpoint of the first element charge to the measurement points. From Fig. 4 it can be easily to find that the measurement points 5 and 1 separately provide minimum and maximum distances from the midpoint of the first element charge, and hence the gauges installed at these two measurement points are triggered as the first and the last ones and then further record the subsequent elemental waves incoming.

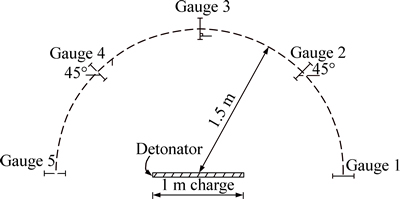
Fig. 4 Geometrical distribution and gauge orientation around cylindrical charge

Fig. 5 Strain waves recorded on five gauges in Fig. 4

Secondly, there is apparent difference among the durations of the first compression phase for the strain waves recorded on gauges, and this is mainly caused by the time difference (△τ=τ_n+1-τ_n , i.e. the time between the successive elemental waves when they arrives at the same measurement point). Take the two strain waves, which are both superposed by 10 equal elements of length 0.1 m and recorded at measurement points 1 and 5, as an example shown in Fig. 6, the time difference between their respective successive elemental waves is same, as shown in Figs. 6(a) and (b), which means both of the time differences △τ₁ and △τ₅ are constants and their equations are derived as

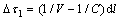                         (8)

                          (9)

Besides that, it is also found that the time difference of the duration for the first compression phase recorded on gauges 1 and 5, is equal to half of the sum of the time differences between their respective successive elemental waves, i.e.

  (10)

and can be simplified as:

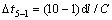                (11)

So, from Eq. (11) it can be seen that the duration of the first compression phase for the strain wave recorded on gauge 5 is obviously larger than that on gauge 1, which agrees well with Fig. 6(c). Furthermore, when these two measurement points are placed along the charge at other opposite distance symmetrically (e.g.2 m), Eq. (11) is still applicable and the value for △τ_5-1 keep constant. In addition, Eq. (11) also indicates that for the strain waves recorded at two measurement points placed symmetrically along the charge, the difference of the duration for the first compression phase is only concerned with the V.O.P. in the surrounding rock of the charge.

Thirdly, the peak value of the strain wave varies apparently with the position of the gauge. It can also be seen from Figs. 6(b) and (c) that the peak values of the 10 elemental waves for superposing strain wave at measurement point 1 are almost the same as that at measurement point 5 when the 10 elemental waves at either measurement point are in reverse order. So, when assume the 10 successive elemental waves for superposing strain wave at measurement point 5 arrive with time interval △τ₁, the superposed strain wave is shown in Fig. 7 and the peak values of strain waves 1 and 5 are basically consistent with each other. It should be noted that the measurement points 1 and 5 are placed at same distance along and from the midpoint of the charge; the sum of attenuation for the respective elemental waves are the same, so the peak values of strain waves 1 and 5 mainly depend on the time interval △τ, and the essential reason for the difference of △τ is obvious the initiating direction, i.e. which end of the charge is detonated. The charge is detonated from left end, and for measurement point 1 each elemental wave travels a shorter distance than its predecessor which leads to a shorter △τ ; for the measurement point 5, it is otherwise. Similarly, when analysis the two strain waves for measurement points 2 and 4 with the way above, except the non-constant △τ between the successive elemental waves which is caused by the non-equal difference R_n, it also can be revealed that the initiating direction is crucial to the peak value.

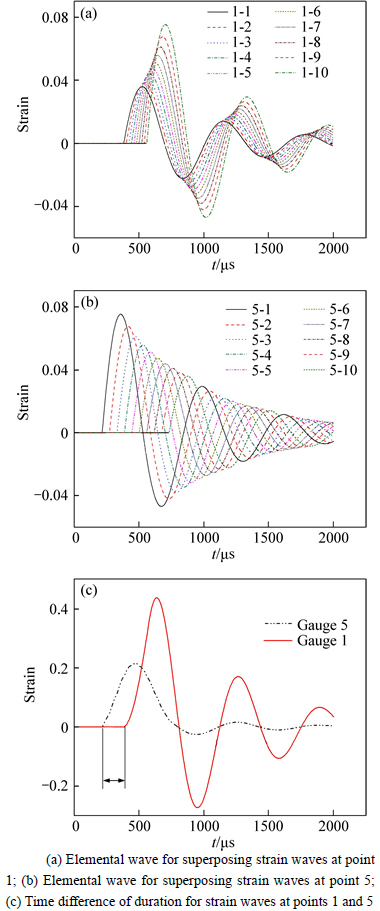
Fig. 6 Time difference of duration for the first compression phase:

As reviewed above, for all the five strain waves recorded at different measurement points, their triggering time, duration of the first compression phase and peak value vary considerably with the gauge position. Especially at measurement points 1 and 5, although these two points are placed symmetrically with the charge, two very different strain waves will be measured because of the opposite propagation along the charge. So, the strain wave generated in rock at large distances from a cylindrical charge is totally dependent on the geometr of the situation and there is much difference in the readings from a point or spherical explosive charge.

Fig. 7 Comparison of strain waves 1 and 5 based on assumption

3.2 Effect of gauge orientation on strain wave

The rising time (time taken for increasing from 0 to peak of compression) and falling time (time taken for falling from the peak of compression to the peak of tension) are considered to be two important factors in evaluating the rock braking propensity of a strain wave. Since in the previous strain wave measurement operations only the unidirectional gauge was available for the wave record, considerable caution associated with the gauge orientation must be taken in the interpretation of the rising time, falling time and peak of strain.

Next, the effect of the gauge orientation on strain wave measured at a strain gauge is continued to be studied. Figure 8 shows the strain waves that should be measured on gauge 3 in Fig. 4 for the orientation of 30° and 60° to either side of the perpendicular. It could be easily found that when the orientation varies at a same measurement point, not only the peak values of compression and tension strains, but also the times at which the peaks appearing are changed.

Furthermore, considering the peak values of strain waves at five measurement points in Fig. 4, except points 1 and 5, the maximum peak values of strain waves are not occurred in the radial direction. Figure 9 shows the strain waves that should be measured on gauges 2, 3 and 4 in Fig. 4 for the orientation of 5° and 10° to either side of the radial direction. It can be seen that the maximum peak values are appeared respectively in the orientation of -5°, 5° and 5° to the radial direction, and this is also caused by the angle φ, at which the unidirectional strain gauge is set, deciding the value of Y_φ in Eq. (6).

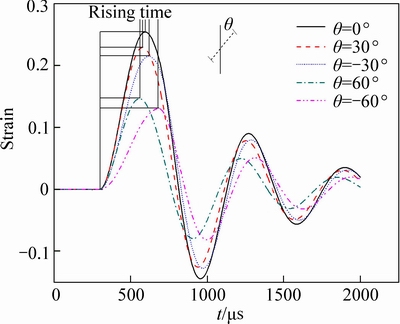
Fig. 8 Effect of gauge orientation on strain wave at a point

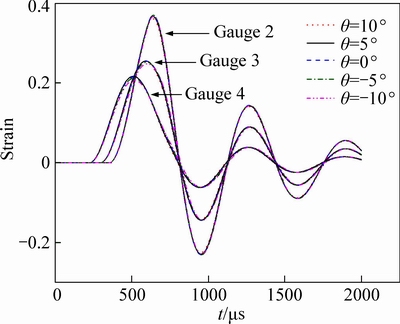
Fig. 9 Gauge orientation of maximum peak value

4 Effect of V.O.D. on strain wave

The strain wave is a function of time, and the V.O.D. directly makes effect on the time taken from initiating of the charge to causing disturbance at target point for each elemental wave in blasting. So, the strain wave at any point is also a function of the V.O.D. of the explosive charge. Figure 10 shows the comparison of strain waves that should be recorded on gauge 3 in Fig. 4 for different V.O.D. with the V.O.P. kept unchanged. It is easily found from the figure that the V.O.D. plays an important part in rock braking if the peak amplitude of a strain wave is an indication of its rock braking characteristics. The peak value of strain wave increases as the V.O.D.. The compression and tension strain varies significantly when the V.O.D. increases during a low level (e.g.2000 m/s-4000 m/s), and it still increases when the V.O.D. at a high level but not that obviously any more.

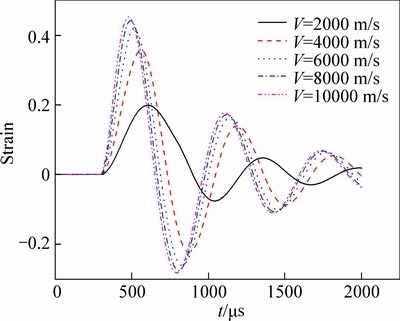
Fig. 10 Variation of strain wave with different V.O.D. values

5 Conclusions

1) Unlike the readings from a point or small spherical explosive charge, the strain wave generated in rock at large distances from a cylindrical charge is totally dependent on the geometry of the situation. Generally, the interactions of the elemental waves vary significantly with the position of the strain gauge, and the strain wave measured at a strain gauge will also vary when the gauge orientation changes.

① Each gauge is triggered at different time after the detonation, and it depends on the time taken for the first elemental wave from the midpoint of the first element charge to the measurement points;

② There is apparent difference among the duration of the first compression phase for the strain waves recorded on gauges, and this is mainly caused by the time difference between the successive elemental waves when they arrives at one same measurement point. In addition, the strain waves recorded at two measurement points placed symmetrically along the charge, the difference of the duration for the first compression phase is only concerned with the V.O.P. in the surrounding rock of the charge;

③ The essential reason for that, the peak value of the strain wave varies with the position of the gauge, is the initiating direction;

④ Except points 1 and 5, the maximum peak values of strain waves are not occurred in the radial direction, the maximum peak values on gauges 2, 3 and 4 are appeared respectively in the orientation of -5°, 5° and 5° to the radial direction.

2) The strain wave at any point is a function of the V.O.D. of the explosive charge. The peak value of strain wave increases as the V.O.D., and it still increases when the V.O.D. at a high level but not that obviously any more.

References

[1] ZHU Zhe-ming, MOHANTY B, XIE He-ping. Numerical investigation of blasting-induced crack initiation and propagation in rocks [J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44: 412-424.

[2] YAN Chang-bin. Blasting cumulative damage effects of underground engineering rock mass based on sonic wave measurement [J]. Journal of Central South University of Technology, 2007, 14(2): 230-235.

[3] XU Guo-yuan, DUAN Le-zhen, GU De-sheng, YAN Chang-bin. Radial explosion strain and its fracture effect from confined explosion with charge of cyclonite [J]. Journal of Central South University of Technology, 2004, 11(4): 429-433.

[4] ALEKSANDROVA N I, SHER E N. Modeling the failure of rock blocks by blasting a cylindrical charge [J]. Journal of Mining Science, 2006, 42(1): 27-34.

[5] YANKELEVSKY D Z, FELDGUN V R, KARINSKI Y S. Underground explosion of a cylindrical charge near a buried wall [J]. International Journal of Impact Engineering, 2008, 35(8): 905-919.

[6] ZHU Zhe-ming, XIE He-ping, MOHANTY B. Numerical investigation of blasting-induced damage in cylindrical rocks [J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45: 111-121.

[7] CAO An-ye, DOU Lin-ming, LUO Xun, ZHENG Yi-dong, HUANG Jun-li, ANDREW K. Seismic effort of blasting wave transmitted in coal-rock mass associated with mining operation [J]. Journal of Central South University of Technology, 2012, 19: 2604-2610.

[8] VOVK A A, KUZMENKO A A. Seismic action of the cylindrical charge explosion [J]. International Journal of Fluid Mechanics Research, 2003, 30(1): 109-122.

[9] LEI Wei-dong, TENG Jun, HEFNY A, ZHAO Jian, GUAN Jiong. Numerical study on maximum rebound ratio in blasting wave propagation along radian direction normal to joints [J]. Journal of Central South University of Technology, 2006, 13(6): 743-748.

[10] ZUO Yu-jun, TANG Chun-an, ZHU Wan-cheng, LI Di-yuan, LI Shu-cai. Numerical analysis of tunnel reinforcing influences on failure process of surrounding rock under explosive stress waves [J]. Journal of Central South University of Technology, 2008, 15(6): 632-638.

[11] SELBERG H L. Transient compression waves from spherical and cylindrical cavities [J]. Ark Fys, 1952, 5: 97-108.

[12] HEELAN P A. Radiation from a cylindrical source of finite length [J]. Geophysics, 1953, 18: 685-696.

[13] BLAIR D P. A comparison of Heelan and exact solutions for seismic radiation from a short cylindrical charge [J]. Geophysics, 2007, 72(2): 33-41.

[14] JORDAN D W. The stress wave from a finite cylindrical explosive source [J]. J Math Mech, 1962, 11: 503-552.

[15] PLEWMAN R P, STARFIELD A M. The effects of finite velocities of detonation and propagation on the strain pulses induced in rock by linear charges [J]. J S Afr Min Metall, 1965, 66: 77-96.

[16] WHITE J E, SENGBUSH R L. Shear waves from explosive sources [J]. Geophysics, 1963, 28: 1001-1019.

[17] STARFIELD A M. Strain wave theory in rock blasting [R]. presented at the Eighth Rock Mechanics Symposium, University of Minnesota, 1966.

[18] ZHONG Guo-sheng, AO Li-ping, ZHAO Kui. Influence of explosion parameters on wavelet packet frequency band energy distribution of blast vibration [J]. Journal of Central South University of Technology, 2012, 19(9): 2674-2680.

[19] KARINSKI Y S, FELDGUN, V R, YANKELEVSKY D Z. Effect of soil locking on the cylindrical shock wave's peak pressure attenuation [J]. Journal of Engineering Mechanics, 2009, 135(10): 1166-1179.

[20] HE Wei, CHEN Jian-yun, GUO Jing. Dynamic analysis of subway station subjected to internal blast loading [J]. Journal of Central South University of Technology, 2011, 18: 917-924.

[21] NIMA B, HAMID M, SAEED K N, MOJTABA B. A coupled method to study blast wave propagation in fractured rock masses and estimate unknown properties [J]. Computers and Geotechnics, 2013, 49: 134-142.

[22] WANG Wei-hua, LI Xi-bing, ZHANG Yi-ping, ZUO Yu-jun. Closure behavior of rock joint under dynamic loading [J]. Journal of Central South University of Technology, 2007, 14(3): 408-412.

[23] LI Qi-yue, LI Xi-bing, WEN Shi-you. Imitating study on blasting effect of jointed rock masses [J]. Journal of Central South University of Technology, 1998, 5(2): 127-129.

[24] SAFFY A A, JOHNSTON H A, MULKE H C. The efficiency of ANBA in comparison with conventional explosives [J]. J SAIMM, 1964, 64: 697.

(Edited by DENG Lü-xiang)

Foundation item: Projects(51304239, 51374243) supported by the National Natural Science Foundation of China

Received date: 2015-11-30; Accepted date: 2016-03-17

Corresponding author: LIU Ke-wei, PhD; Tel: +86-18229726328; E-mail: kewei_liu@csu.edu.cn