基于二维变形体入水的滑行艇水动力研究
王硕，苏玉民，张曦，蒋一
(哈尔滨工程大学 水下智能机器人国防重点实验室，黑龙江 哈尔滨，150001)
摘要：为寻找准确便捷估算滑行艇水动力的方法，在二维半理论的简化模型下，通过CFD方法建立气液二相流VOF模型，数值模拟二维变形体入水砰击过程，对滑行艇稳定直航状态下的动升力进行研究。为验证数值模型精度，首先对二维楔形体入水进行数值模拟，并将得到的砰击参数与理论近似解结果进行比较，进而根据船模实验中的航行姿态，将三维船体稳定直航简化为二维变形横剖面入水过程并通过动网格技术进行数值模拟。将变形横剖面入水不同时刻的动升力沿船长方向对应的横剖面位置进行积分得到全艇的动升力。同时，对三维船体进行绕流计算，将得到的动升力与二维积分结果以及实验值进行对比。计算结果表明，二维和三维计算结果均与实验数据基本吻合，通过CFD方法计算基于二维变形体入水的高速滑行艇水动力问题具有可行性。
关键词：二维半理论；VOF模型；二维变形体；入水砰击; 动网格技术
中图分类号：O357 文献标志码：A 文章编号：1672-7207(2013)07-2764-07
Hydrodynamic of planing craft based on 2D deforming body entering water
WANG Shuo, SU Yumin, ZHANG Xi, JIANG Yi
(State Key Laboratory of Autonomous Underwater Vehicle, Harbin Engineering University, Harbin 150001, China)
Abstract: In order to find an accurate and convenient method to evaluate the hydrodynamic forces of planing craft, the body lifts of the planing craft in the steady sailing situation was researched based on the VOF model including air and water built up with the CFD method under the simplified model of the 2.5D theory. To validate the accuracy, the 2D wedge bodies entering water were calculated first and the lifts parameters were compared with the approximate theory. The three dimension hull sailing in the calm water was transformed into a deforming section entering water. The deforming section entering water was simulated with dynamic mesh technique. By integrating the lifts in different time of the section along the ship longitude, the dynamic lift of the hull was obtained. Meanwhile, the numerical simulation of three dimension planing craft sailing in calm water was calculated and the results of lifts at different speeds were compared with the two dimension results and experiment data. The results show that the 2D and 3D results both match the experiment data. It is feasible to use the numerical method with CFD technique to calculate the hydrodynamic of planing craft in high speed based on two dimension deforming body entering water.
Key words: 2.5D theory model; VOF model; 2D deforming body; water entry; dynamic mesh technique
随着海洋以及濒海资源战略地位的日益凸显，载人和无人高速艇得益于其高速灵活等特性，受到越来越多的关注和应用。关于滑行艇水动力性能的计算与研究，也成为水动力学研究的热点。由于滑行艇的高速和砰击特性，常规船型的水动力预报方法不再适用，因此需要寻找新的计算方法，准确地估算滑行艇的水动力性能。滑行艇直航时的稳态行为是首先引起关注的问题，此时滑行艇所受的升力以水动压力为主，水静压力比重很小。近年来，CFD技术已被广泛应用于滑行艇水动力性能的研究，但对于三维的滑行艇数值仿真需要花费大量的计算机时间，对于大作业量预报效率有限。Zhao等[1]采用非线性边界元理论研究了任意形状的二维结构的入水问题，采用时间步进法求解了积分形式的二阶格林等式，入水角的计算范围扩展至4°~81°，并且对计算模型中质量、动量和能量守恒问题进行了校核，计算结果与Dobrovol’skaya的结果吻合较好。1996年Zhao等[2]在楔形体喷溅根部引入一个垂直于物体表面的控制面，并把流动在棱角的分离包括进去，使得计算结果更加精确。1997年Zhao和Faltinsenr[3]提出了一种基于势流理论的二维半理论方法用于求解滑行艇水动升力问题，随后Sun等[4-6]应用该方法对滑行艇水动力问题进行了深入研究，计算了滑行艇在静水及波浪中的运动规律。马山等[7]对基于势流理论的二维半方与切片法进行了比较。张军等[8]较早运用CFD方法对二维楔形体入水初期进行数值模拟。陈震等[9]对二维楔形体入水砰击的CFD计算取得了较高的计算精度。陈小平等[10]利用MSC.Dytran软件对二维楔形体入水进行了流固耦合计算。与基于势流理论边界元方法的二维半理论不同，本文作者应用基于有限体积法求解雷诺平均纳维-斯托克斯(RANS)方程的CFD商业软件Fluent，利用二维半理论的简化模型，将滑行艇稳定直航问题简化为二维平面内变形横剖面入水砰击问题，计算中考虑了黏性效应。为验证二维砰击问题计算精度，先计算了二维楔形体入水时产生的动升力。通过楔形体入水砰击计算对本文数值模型进行验证其可行性后，再应用此算法计算滑行艇的稳定直航动升力并同三维数值结果比较。在求解过程中建立了VOF多相流模型，并采用了动网格技术控制入水剖面形状随时间的变化和垂向位移。其中计算滑行艇的动升力时，航行姿态全部来自水池模型拖曳试验的结果，因此得到的动升力计算结果可直接同模型自重进行比较，得到相对误差。
1 数值计算模型
滑行艇静水直航模型如图1所示。根据Zhao[3]提出的二维半即2D+t理论，当滑行艇行驶于静水面时，考虑船前方一固连于大地的横平面，平面内流体未受船体扰动，当滑行艇通过这个平面时，将船体对此平面内流体的扰动看作是一变形的二维横剖面垂向入水对水的作用，见图2。通过将三维船体的直航运动换算为二维变形横剖面入水，记录变形横剖面入水过程中各个时刻的垂向力，即可换算为到船体沿纵向不同位置的水动升力，然后沿船长积分，得到全船的水动升力(考虑重力包括静浮力)。计算围绕二维剖面展开，同时满足了三维边界条件，考虑了切片间的影响，因此称之为二维半理论。
因为滑行艇直航时浸水部分形状沿船长方向变形较小，可通过CFD方法中动网格技术实现变形二维横剖面垂直入水的运动过程。因此，本文在二维半理论模型的基础上，采用CFD方法对二维变形船体横剖面进行砰击入水的数值模拟。计算中，设定滑行艇以一稳定速度直航于静水面，沿船长将全船纵倾角分为若干段，不同纵倾角下，二维横剖面入水速度不同，垂向速度为
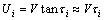(1)
式中：Ui为横剖面入水垂向速度；V为船模航速；τi为全船纵倾角；
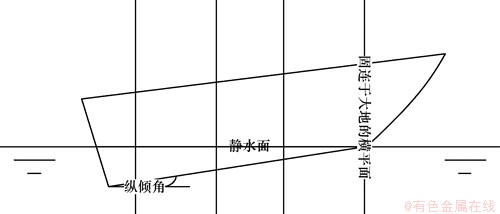
图1 滑行艇静水直航模型
Fig.1 Model of planing craft sailing in calm water
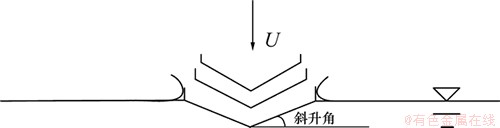
图2 二维变形剖面入水砰击过程
Fig.2 Water entry procedure of 2D deforming section
在横剖面匀速向下运动的过程中，船型剖面由船首的形状逐渐向尾部形状过渡，每一时刻的形状与入水高度及横剖面位置一一对应。本文计算的某滑行艇型，其水下体积为近似棱柱面，沿船首至船尾，横剖面近似为斜升角不断减小的楔形体。因此，本文对于二维横剖面的变形，运用斜升角随时间变化的分段函数确定横剖面的形状。横剖面斜升角沿船首至船尾的变化非均匀变化，须沿船长分段设定变形函数，每段内认为斜升角随下落时间线性变化。变形函数为
(2)
(3)
式中：y(t)，x(t)为船型横剖面纵向、横向坐标；y0，x0为初始坐标位置；U(t)为横剖面下落速度；β0为初始纵倾角；ωj为不同分段内斜升角变化率。
为验证本文数值模拟计算的可靠性，先应用此计算模型对特定斜升角的楔形体入水进行计算。根据相关数值和实验研究可知，楔形体入水时的动升力只与斜升角、入水速度、水的密度和入水时间有关。因此，设定以上条件相似，将楔形体置于自由液面之上近液面处，令楔形体以固定速度匀速直线垂直向下运动，运动过程中记录整个砰击入水全过程，监测楔形体所受的垂向力，模型设定中考虑重力影响，得到的垂向力中包含了静压力和动压力。将计算结果同理论解进行比较，验证CFD数值模拟二维砰击的计算精度，再结合动网格技术应用于实艇的计算，并与实验值进行对比。
2 数值方法
2.1 控制方程
对于不可压缩的黏性流动，在笛卡儿坐标系下，用张量的形式表示的时均连续性方程和RANS方程可以写为：
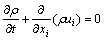(4)
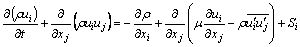
(i, j=1, 2, 3) (5)
式中：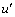
为速度分量的时均值；
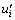为速度分量的脉动值；
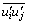为速度分量乘积的时间平均值；μ为流体的动力黏性系数。
计算域上方边界设置为压力出口(pressure outlet)，其余边界皆为固壁条件(wall)。计算步长取0.1 ms，以保证计算精度[11-14]。
2.2 计算网格
对于计算网格的划分，采用结构网格与非结构网格混合布置方法(见图3)。在横剖面附近水平设置矩形区域作为随体，随体内部采用非结构网格，随体外部计算域采用结构化网格。在模拟二维物体入水时，随体伴随物体同时下落，通过结构网格的Dynamic Laying动网格模型实现二维物体垂向运动。
图3 二维剖面计算网格
Fig.3 Mesh of two dimension section
对于横剖面在下落过程中的变形，则通过随体内非结构网格的弹性变形实现，垂直下落和变形2种运动方式分别由2个不同的方程控制。对于楔形体入水模拟的网格，则仅设定随体滑移网格运动，随体内网格形状保持不变。对动网格的设置要采用Fluent软件中的UDF函数中的GRID MOTION宏控制斜升角的变化以及垂直向下运动。
2.3 计算可行性验证
为验证本文CFD方法对二维物体入水砰击过程数值计算的准确性。在对实艇进行计算之前，首先对固定斜升角的二维楔形体入水砰击进行计算。将计算结果同理论近似解进行比较，验证精度后，再基于二维半理论的简化模型，对二维变形滑行艇横剖面进行数值计算。由于本文艇形的横剖面斜升角平均值为20°~25°，因此，计算楔形体入水时分别采用斜升角等于20°和25°的楔形体用来验证其可行性。
预先设定楔形体的入水速度为0.4 m/s，流域为6 m×6 m的正方形，上半部为空气，下半部为水。令楔形体以一定恒定速度入水，根据DobrovolSkaya的相似解[3]，当流体在折角线处未发生分离之前，入水砰击力参数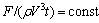
，20°，25°时，该参数分别等于42.485和23.657。计算域上方为压力入口，其他三周定义为壁面边界条件，楔形体定义为刚性物体，参考压强设为大气压。运用上文所述的滑移动网格进行计算。二维楔形体入水示意图见图4。楔形体入水后，砰击液体，产生飞溅，入水砰击所受的砰击力随时间变化如图5所示。可见，入水初期，动升力随入水时间呈线性增长。直到发生根溅后，动升力呈非线性下降。
将得到的动升力做无因次化处理，得到砰击参数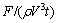
，将其与理论近似解比较，见图6。
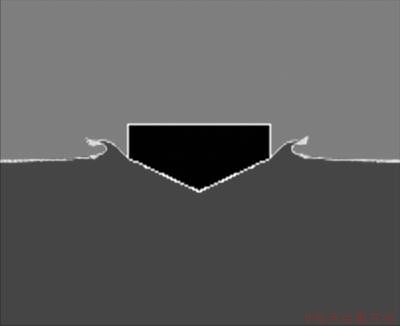
图4 二维楔形体入水示意图
Fig.4 Sketch map of water entry of two dimension wedge body
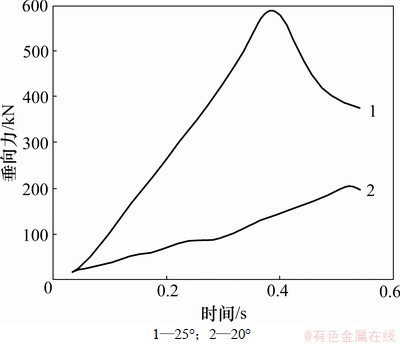
图5 入水垂向力随时间变化
Fig.5 Impact force with time of water entry
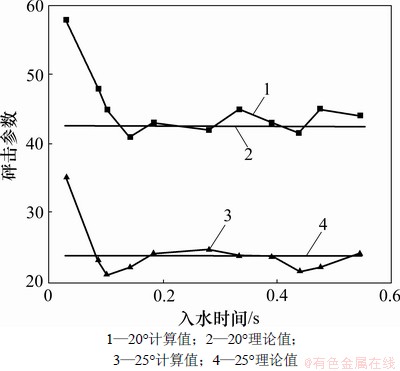
图6 20°和25°斜升角楔形体砰击参数
Fig.6 Impact coefficient of wedge body with 20°and 25°
由图5和6可知，在楔形体入水初期，砰击参数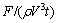一直保持常数，模拟过程中液面变化与垂向力监测值均与理论解符合良好。说明本文中的数值模型能够比较准确的估算出二维物体入水砰击时所受的水动升，进而应用于实艇动升力的估算。
3 数值计算结果与分析
3.1 航行姿态的确定
在二维楔形体入水模拟的基础上建立二维变形体入水砰击模型，加入非结构动网格模拟横剖面变形运动，采用的数值计算参数与计算楔形体入水基本相同。为验证二维计算方法的可行性，采用船模实验中的航行姿态进行计算，计算结果可直接与实验值对比。4种航速下的结果见表1。
表1 拖线方式静水直航实验数据记录
Table 1 Data of modeling experiments
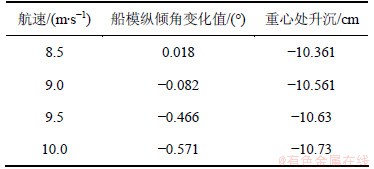
数值计算在考虑重力的情况下进行，计算所得的动升力中包含静浮力，可直接与船模自身重力进行比较。此实验在中国特种飞行器研究所(605所)拖曳水池进行，模型采用玻璃钢复合材料制作拖曳试验中的滑行艇模型(见图7)。实验用高速水池长510 m，池宽6.5 m，池深6.8 m，水深5.0 m。拖车速度为0.5~22 m/s。
图7 拖曳水池船模试验
Fig.7 Experiment of planing craft in tolling tank
3.2 二维横剖面的获得及控制剖面变形函数的确定
根据船模实验中不同航速下的不同航行姿态，设定船模的纵倾角，截得不同航行姿态下的各船型横剖面见图8。在纵剖面内将全船纵倾角分为若干段，不同纵倾角下得到横剖面不同的入水速度。同时量取横剖面斜升角，确定相邻两横剖面间斜升角变化速率随时间呈线性变化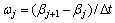
。在实际二维计算中，为减少网格数，将本艇模防撞气垫以上部分截去不计，并不影响计算水动力性能。
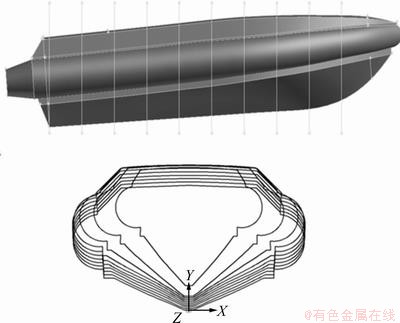
图8 获得二维剖面
Fig.8 2D section from model
3.3 二维变形横剖面入水砰击
在得到各航态下的船模横剖面运动规律后，将其运动函数写入网格运动程序中。应用二维数值模型对船模变形横剖面做入水砰击数值模拟，监测剖面垂向力，并整理数据得到垂向力积分区间，便可沿船长积分得到全船垂向力。图9所示为航速为10 m/s时二维变形横剖面入水全过程，砰击过程与产生飞溅与二维楔形体入水相似。
3.4 计算结果比较分析
图10所示为4个航速下船模变形横剖面入水过程中监测到的垂向力。4个航速下的船模航行姿态相近，得到的垂向力分布趋势也比较相近。最大垂向力分布出现在船首即二维剖面入水初期，此时全船纵倾角变化较大，虽然入水面积较小，但入水速度较快。船中后部分全船纵倾角变小且基本相同，砰击力呈线性递增，与楔形体入水砰击相似。
对横剖面各时刻所对应船模纵向位置的垂向力沿船长积分，得到船模在该航速下的全船动升力(包含静浮力)。由于船模拖曳过程中保持垂向力平衡，所以得到的垂向力应该同船模自身重力平衡。因此，本文将数值积分得到的垂向力跟船模自身重力1 140 kN进行对比，便可以得到本算法的计算误差和精度。
为进行比较分析，本文同时运用三维绕流模型按照同样的航行姿态计算了船模升力，同二维结果以及实验值进行比较，航速10.0 m/s时绕流计算自由液面及压力分布云图见图11。图12所示为三维绕流计算中船模剖面的两相流分布图。各剖面与图9中的各个时刻对应，可以对比二维等效计算和三维数值模拟的差异。
比较图9与图12可知，二维变形剖面入水与三维滑行艇直航是等效的。二维剖面入水过程中的每一时刻对应了三维直航船模不同的横剖面位置。但二维砰击和三维绕流的自由液面形状还有一定差异。二维变形剖面入水产生的横向飞溅更为明显，而三维计算的流场截面包含了纵向的飞溅效果。由于二维简化模型的局限性，三维计算中沿船长方向的飞溅是二维方法捕捉不到的。这对计算结果会产生一定影响。
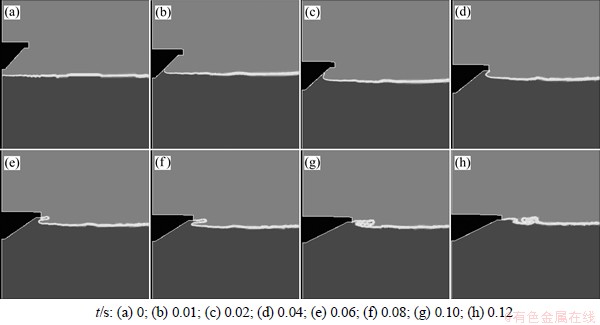
图9 二维变形剖面入水全过程
Fig.9 Procedure of water entry of 2D deforming section
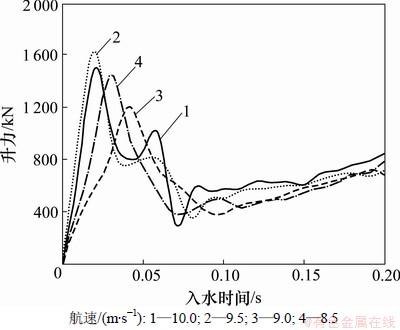
图10 剖面入水垂向力
Fig.10 Lifts of water entry of sections
由图10得知，不同航速下的滑行艇受力分布不同，但总垂向力均接近船模自身重力。对高速航行姿态下得到的动升力与船模自身重力进行比较，结果见表2和3。
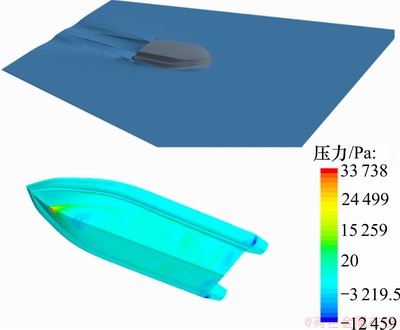
图11 10.0 m/s自由表面和滑行艇压力分布
Fig.11 Free surface and pressure distribution of planing craft in 10.0 m/s
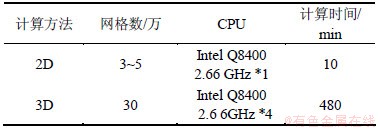
由表2和表3可知，基于二维变形体入水砰击的数值方法可以较准确地估算出滑行艇的动升力。由于其为二维简化模型，其计算精度较三维绕流计算精度仍有一定差距。但二维计算方法减少了计算机时间，可以快捷定性用于计算滑行艇水动力问题。
二维模型的计算误差可能来自于：(1) 数值模型本身的误差，如几何模型的差异, 计算网格变形引起的误差，VOF模型中自由液面的误差等等；(2) 二维计算虽然考虑了三维边界条件和剖面之间的影响，但二维变形剖面处理时对三维船型进行了化简，且二维方法无法模拟纵向飞溅等现象，固存在误差；(3) 拖曳模型试验本身设备仪器误差以及测量误差等。
图12 航速10.0 m/s时横剖面附近气液两相流分布
Fig.12 Distribution of water and air around sections at speed of 10.0 m/s
表2 全船升力计算结果
Table 2 Calculation results of lifts
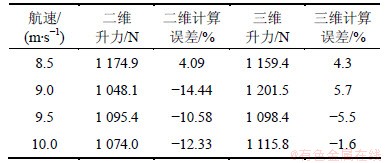
表3 计算机资源使用情况
Table 3 Occupation of CPU resourses
4 结论
(1) 应用CFD数值计算模型对二维物体入水砰击的数值计算结果具有较高精度。
(2) 将基于势流理论的二维半理论的物理模型提取出来，应用CFD方法将三维船模稳定直航问题等价为二维变形横剖面入水进行水动升力计算是可行的，计算结果准确，计算效率较高。
(3) 本文的二维计算与三维CFD计算结果均满足工程精度，二维精度低于三维结果，但节省了大量计算机时间，可以更便捷地估算高速滑行艇水动力参数。
(4) 二维方法的计算精度仍有待提高，对三维船型化简为二维变形剖面入水的简化过程仍应做进一步细化，动网格控制函数需继续完善，以提高计算精度。
参考文献
[1] Zhao R, Faltinsen O M. Water entry of two-dimension bodies[J]. Journal of Fluid Mechanics, 1993, 246: 593-612.
[2] Zhao R, Faltinsen O M. Waterentry of arbitary two-dimensional sections with and without flow separation[C]// Proc 21st sympon Naval Hydrodynamics. Washington D C: National Academy Press, 1996: 408-423
[3] Zhao R, Faltinsen O M, Haslum H. A simplified non-linear analysis of a high-speed planing craft in calm water[C]// FAST’97. London: Baird Publications, 1997: 431-438.
[4] SUI Hui, Faltinsen O M. The influence of gravity on the performance of planning vessels in calm water[J]. J Eng Math, 2007, 58: 91-107.
[5] SUN Hui, Faltinsen O M. Hydrodynamic forces on a planning hull in forced heave or pitch motions in calm water[C]// 22nd IWWWFB. Plitvice, Croatia, 2007: 185-188.
[6] SUN Hui, Faltinsen O M. Numerical study of planning vessels in waves[C]// 9th International Conference on Hydrodynamics. Shanghai, 2010: 468-475.
[7] 马山, 宋竞正, 段文洋. 二维半理论和切片法的数值比较研究[J]. 船舶力学, 2004, 8(1): 35-43.
MA Shan, SONG Jingzheng, DUAN Wenyang. Comparison of 2-1/2D theory and N.S.M. applied for high-speed ships[J]. Journal of Ship Mechanics, 2004, 8(1): 35-43.
[8] 张军, 张志荣, 洪方文, 等. 楔形体入水初期流场的数值模拟[J]. 船舶力学, 2003, 7(4): 28-35.
ZHANG Jun, ZHANG Zhirong, HONG Fangwen, et al. Numerical simulation of initial flow of wedge entry[J]. Journal of Ship Mechanics, 2003, 7(4): 28-35.
[9] 陈震, 肖熙. 二维楔形体入水砰击仿真研究[J]. 上海交通大学学报, 2007, 41(9): 425-428.
CHEN Zhen, XIAO Xi. The simulation study on water entry of 2D wedge bodies[J]. Journal of Shanghai Jiaotong University, 2007, 41(9): 425-428.
[10] 陈小平, 滕蓓. 二维楔形体入水砰击的数值仿真[J]. 舰船科学技术, 2010, 32(1): 120-124.
CHEN Xiaoping, TENG Bei. Numerical simulation about water entry of 2D wedge bodies[J]. Ship Science and Technology, 2010, 32(1): 120-124.
[11] 傅慧萍, 马宁. 自由面及伴流计算对网格的要求[J]. 上海交通大学学报, 2009, 43(10): 1573-1576.
FU Huining, MA Ning. Demands of free surface and wake computation on mesh[J]. Journal of Shanghai Jiaotong University, 2009, 43(10): 1573-1576.
[12] 傅慧萍, 杨晨俊. 雷诺数对船舶阻力和伴流场的影响[J]. 上海交通大学学报, 2009, 43(10): 1555-1663.
FU Huining, YANG Chenjun. The effects of reynolds number on resistance and wake of ship[J]. Journal of Shanghai Jiaotong University, 2009, 43(10): 1555-1663.
[13] 张志荣, 李百齐, 赵峰. 船舶粘性流动计算中湍流模式应用的比较[J]. 水动力学研究与进展, 2004, 19(5): 1-3.
ZHANG Zhirong, LI Baiqi, ZHAO Feng. The comparison of turbulence models applied to viscous ship flow computation [J]. Chinese Journal of Hydrodynamics, 2004, 19(5): 1-3.
[14] 朱德祥, 张志荣, 吴乘胜, 等. 船舶CFD不确定度分析及ITTC临时规程的初步应用[J]. 水动力学研究与进展, 2007, 22(3): 363-370.
ZHU Dexiang, ZHANG Zhirong, WU Chengsheng, et al. Uncertainty analysis in ship CFD and the primary application of ITTC procedures[J]. Chinese Journal of Hydrodynamics, 2007, 22(3): 363-370.
(编辑 赵俊)
收稿日期：2012-07-04；修回日期：2012-11-15
基金项目：国家自然科学基金资助项目(510090384)；高等学校博士学科点专项科研基金资助项目(200802170010)
通信作者：王硕(1987-)，男，北京人，博士研究生，从事流体力学、高性能船等研究；电话：18646159587；E-mail: marvin_heu@163.com
