Job shop scheduling problem with alternative machines using genetic algorithms
来源期刊:中南大学学报(英文版)2012年第5期
论文作者:I. A. Chaudhry
文章页码:1322 - 1333
Key words:alternative machine; genetic algorithm (GA); job shop, scheduling; spreadsheet
Abstract:
The classical job shop scheduling problem (JSP) is the most popular machine scheduling model in practice and is known as NP-hard. The formulation of the JSP is based on the assumption that for each part type or job there is only one process plan that prescribes the sequence of operations and the machine on which each operation has to be performed. However, JSP with alternative machines for various operations is an extension of the classical JSP, which allows an operation to be processed by any machine from a given set of machines. Since this problem requires an additional decision of machine allocation during scheduling, it is much more complex than JSP. We present a domain independent genetic algorithm (GA) approach for the job shop scheduling problem with alternative machines. The GA is implemented in a spreadsheet environment. The performance of the proposed GA is analyzed by comparing with various problem instances taken from the literatures. The result shows that the proposed GA is competitive with the existing approaches. A simplified approach that would be beneficial to both practitioners and researchers is presented for solving scheduling problems with alternative machines.
J. Cent. South Univ. (2012) 19: 1322-1333
DOI: 10.1007/s11771-012-1145-8![]()
I. A. Chaudhry
National University of Sciences and Technology, Islamabad, Pakistan
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: The classical job shop scheduling problem (JSP) is the most popular machine scheduling model in practice and is known as NP-hard. The formulation of the JSP is based on the assumption that for each part type or job there is only one process plan that prescribes the sequence of operations and the machine on which each operation has to be performed. However, JSP with alternative machines for various operations is an extension of the classical JSP, which allows an operation to be processed by any machine from a given set of machines. Since this problem requires an additional decision of machine allocation during scheduling, it is much more complex than JSP. We present a domain independent genetic algorithm (GA) approach for the job shop scheduling problem with alternative machines. The GA is implemented in a spreadsheet environment. The performance of the proposed GA is analyzed by comparing with various problem instances taken from the literatures. The result shows that the proposed GA is competitive with the existing approaches. A simplified approach that would be beneficial to both practitioners and researchers is presented for solving scheduling problems with alternative machines.
Key words: alternative machine; genetic algorithm (GA); job shop, scheduling; spreadsheet
1 Introduction
Scheduling involves the allocation of resources over a period of time to perform a collection of tasks. It is a decision-making process that plays an important role in most manufacturing and service industries. An effective schedule enables the industry to utilize its resources effectively and attain the strategic objectives as reflected in its production plan.
A real job shop has many complicating factors. There may be multiple machines that can process the same job or operation. Hence, there are several different routings. When the issue of alternative routing or flexibility of routing is added, the problem is more complicated. Each job has a set of precedence- constrained operations to be processed. Although the alternative routing imposes more complexity to the problem, it significantly improves performance if idle machines can alleviate the pressure on other overloaded machines.
In order to decrease job lateness, sets of different jobs have to be planned with different routings. To increase the system throughput rate, a manufacturing system has to include various sets of identical machines processing jobs in parallel. Each of these ‘work-centres’ performs in parallel the operations planned for this category of identical machines. This is ‘flexible routing’ and is normally found in flexible manufacturing systems (FMS). Routing flexibility achieves the following advantages [1-2]:
1) The total manufacturing time is shortened;
2) The work-in-process is reduced;
3) Lead time is reduced;
4) Overall machine utilization is improved.
The job shop problem with alternative routings can be described as follows: there are a set of machines and a set of jobs consisting of chain of operations, each of which needs to be processed. Each machine can process at most one operation at a time and each operation can be processed at more than one machine with different fixed processing time or cost. This is called alternative routing. An alternative operation could be used if one machine tool is temporarily overloaded while another is idle. The alternative routing is useful where capacity problem arises. Even though alternative operations may incur time penalties, they may be used to offload bottleneck machines with the objective of balancing machine utilization and the flow of work pieces.
In this work, we deal with the scheduling problem in a job shop environment where several machines exist and jobs consist of chain of operations to be processed on more than one machine. This work uses spreadsheet based domain independent genetic algorithm (GA) for the scheduling problem with alternative operations in a job shop environment.
2 Previous approaches for alternative machine environment
WIHELM and SHIN [3] performed a study to investigate the effectiveness of alternative operations in flexible manufacturing systems. They showed that alternate operations could reduce flow time while increasing machine utilization. HANKINS et al [4] also discussed the advantages of using alternative machine tool routings to improve the productivity. They showed that using alternative machines results in reducing lead-time and thus improving overall machine utilization.
Among the heuristics to solve job shop problem with alternative routings, NASR and ELSAYED [1] developed an efficient heuristic to minimize the mean flow time in a general job shop type machining system with alternative machine tool routings. AHN et al [5] developed a heuristic algorithm for a scheduling problem with and without alternative operations. The effect of alternative operations on the performance of schedules generated is studied with various dispatching rules. KIM and EGBELU [6] proposed two local search heuristics to solve the job shop problem with alternate routing in order to minimise makespan time.
RAJAMANI et al [7] considered a generalized group technology problem of manufacturing and developed three integer programming models to successively study the effect of alternative process plans and simultaneous formation of part families and machine groups. JIANG and HSIAO [8] used 0-1 integer programming approach in their solution to minimize absolute deviation from due date and sum of finishing times of all the jobs. KIM and EGBELU [9] presented a mixed integer programming model for scheduling a set of jobs through a shop when each job is supplied or provided with multiple process plans or process routings. CHOI and CHOI [10] considered alternative routes and sequence dependent setups together. They developed a mathematical programming model and a local search algorithm using dispatching rules with an objective of minimizing makespan. CHEN and PAN [11] described the development of a mixed binary integer programming (BIP) model for scheduling alternative operations in two-machine flow-shop problems with mean tardiness as the criterion.
THOMALLA [12] solved the job shop scheduling problem with alternative routes using Lagrangian relaxation. The largest problem solved is six jobs, six machines, and ten operations per job with the objective to minimize the sum of the weighted quadratic tardiness of the jobs.
DAUZ?RE-P?R?S and PAULLI [13] considered an integrated approach for assigning machines and scheduling the parts using a tabu search algorithm with a new neighborhood structure. LOGENDRAN and SONTHINEN [14] proposed tabu search based heuristic for scheduling parts in a job-shop type FMS. BILGE et al [15] considered a scheduling problem for a set of independent jobs with sequence dependent setup times on a set of uniform parallel machines and employ a tabu search approach to tackle this problem. SCRICH et al [16] developed two heuristics based on tabu search for scheduling jobs in a flexible job shop with the objective of minimizing total tardiness. CAO et al [17] considered a parallel machine selection and job scheduling to minimize the machine cost and job tardiness. They developed a tabu search method heuristic algorithm to find the optimal or near optimal solutions. MEHRABAD and FATTAHI [18] presented a tabu search algorithm that solves the flexible job shop scheduling problem to minimize the makespan time.
CANDIDO et al [19] considered alternative routes by dividing the routes into sub-processes, where every sub-process is a technologically similar sequence of operations. They proposed a simple hill climbing algorithm to find the local minimum makespan and then a GA was used to further minimize the makespan. ZHAO and WU [20] suggested a GA to solve the job-sequencing problem for a production shop that is characterized by flexible routing and flexible machines. ROSSI and DINI [21] also presented a GA for generalized job-shop problem solving. The generalization includes feeding times, sequences of set-up dependent operations and jobs with different routings among work centres including `multi-identical’ machines. KIM et al [22] proposed a symbiotic evolutionary algorithm for scheduling job shop flexible manufacturing systems integrated with process planning. Each individual in their proposed algorithm consists of two chromosomes with different lengths, where one is involved in the operation sequence for the completion of a job and the other is responsible for machine assignments. TAVAKKOLI- MOGHADDAM et al [23] introduced a new mathematical programming model for a multi-criteria parallel machine scheduling problem. The objective function was to minimize the total earliness/tardiness penalties and machine costs simultaneously. They developed a meta-heuristic method based on genetic algorithms (GAs) to solve such a hard problem. BASKAK and EROL [24] also used GA for a flexible JSP. HUSSAIN and JOSHI [25] proposed a two-pass GA to solve the job shop problem with alternate routing. The first pass picks the alternatives using a GA, and the second pass provides the order and start time of jobs on the selected alternatives by solving a non-linear program. The objective is minimising the sum of squared weighted due date deviation for every job. JAWAHAR et al [26] proposed a search heuristic for scheduling flexible manufacturing systems associated with alternate routing. The proposed heuristic first selects randomly a route for each operation and then a GA-based algorithm, evolves a priority dispatching rule for each machine to resolve the conflicts that arise in the schedule generation procedure.
BECK and FOX [27] proposed a constraint-directed scheduling technique to deal with the case where the scheduling problem includes alternative activities. FERREIRA and WYSK [28] carried out an investigation using simulation and design of experiments techniques for alternative plans on a single machine. SAYGIN et al [29] presented an algorithm, the Dissimilarity Maximization Method (DMM), to solve a real-time rescheduling problem that arises due to machine breakdowns and other unexpected occurrences on the shop floor. The goal of the research is to maximize the throughput rate.
DEMIR [30] considered scheduling and process planning functions concurrently and proved the benefit of flexible process planning and integration. They compared random search, genetic search and hybrid search techniques with ordinary solutions. Results proved that integrated solutions and search techniques outperform ordinary and nonintegrated solutions.
ROSSI and DINI [31] proposed an ant colony optimisation-based software system for solving FMS scheduling in a job-shop environment with routing flexibility, sequence-dependent setup and transportation time
LOW et al [32] addressed a two-stage hybrid flowshop scheduling problem with unrelated alternative machines. The problem had m unrelated alternative machines at the first machine center followed by a second machine center with a common processing machine in the system. The objective was to minimize the makespan of the system. Firstly, they demonstrated that the problem is NP-hard and then provides some heuristic algorithms to solve the problem efficiently.
3 Problem and assumptions
For an alternative machine environment, the system consists of m machines and n different jobs. All jobs are processed under a predetermined technological order given in the process plan. Ji operations are required to finish job i. Each of these operations can be processed on a number of alternative, identical or non-identical machines. The detailed assumptions are as follows.
1) Jobs are independent and consist of strictly ordered operation sequences; no priorities are assigned to any job type.
2) Job pre-emption or cancellation is not allowed.
3) A given operation can be performed by one or more different identical or non-identical machines.
4) Setup times are independent of operation sequence and are included in processing times.
5) All jobs are simultaneously available at time zero.
6) After a job is processed on a machine, it is transported to the next machine immediately and the transportation time is negligible.
7) Each operation has a definite work content and operational time.
8) At most one operation can be processed on one machine at one time.
4 Genetic algorithms and production scheduling
Genetic algorithms (GAs) are directed random search algorithms based on the mechanics of natural selection and natural genetics. GAs are efficient search procedures that can identify optimal or near optimal solutions from solution populations. GAs operate as an iterative procedure on a fixed size of population of candidate solutions called chromosomes. In each iteration, the best solutions (chromosomes) are allowed to produce new solutions (children) by using the bits and pieces of each parent (by crossover) or by occasionally mutating features of a single parent. The worst members of the population die off to make way for the fitter individuals.
GAs were originally developed by HOLLAND [33], at the University of Michigan. In the category of random search techniques, GAs represent a class of search algorithms, which have shown great promise in the field of artificial intelligence.
Detailed study of GAs can be found in Ref. [34]. Applications are found within the general fields of importance to manufacturing such as: 1) scheduling of manufacturing shops, 2) design of machine controllers, 3) factory layouts, and 4) optimisation of objective functions within operations management.
One of the earliest applications of GAs to scheduling was reported by DAVIS [35]. There is a vast literatures available for GA application in production scheduling. Detailed reviews of some of the recent GA application in scheduling are given by CHAUDHRY and DRAKE [36-37] and CHAUDHRY [38].
The authors have found that a key advantage of the proposed GA is that it provides a ‘general purpose’ solution to the scheduling problem, with the peculiarities of any particular example being accounted for in the fitness function without disturbing the logic of the standard optimization routine. This means that it is a relatively straight forward and simple method to adapt the software implementation of the method to meet the needs of particular application.
The work presented here was carried out using the Microsoft? Excel? spreadsheet and an add-in to provide the GA. This add-in is called Evolver?. The details of the software are given in Ref. [39]. It implements the sequence optimization GA described later and acts upon tables of the Microsoft? Excel?. The use of this proprietary software demonstrates how simple it is to implement the GA approach to schedule optimization and also enables the immediate implementation of the method presented here. This is a key aspect of this work.
The main advantage of the proposed GA approach is that it is an independent general purpose domain meaning that only the spreadsheet model needs to be changed to suit a particular manufacturing environment rather than the whole GA routine itself. Furthermore, the objective function can be changed without changing the model or the GA routine. The presentation of information to user in the form of well defined spreadsheet tables makes it easier for the user to carry out what-if analysis. Also, the use of spreadsheets is welcomed by production managers as they are used to this kind of tools. We have to take into account the fact that the scheduling solutions provided will be used by non-skilled workers.
The model of the scheduling environment presented in this work is built in EXCEL? using the spreadsheet’s built-in functions. After the building of the model, the GA is run to optimize the schedule based on a given objective function.
Figure 1 illustrates the schematic integration of the GA with the spreadsheet.
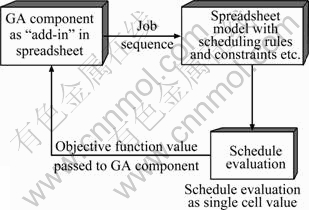
Fig. 1 Spreadsheet-GA integration
The fitness/objective function value is passed on to the GA component as a single cell value for the evaluation of the schedule. After evaluation, if the schedule is found to have better fitness as compared to the other organisms in the population, it is kept in the population, thus replacing the worst performing member of the population.
5 GA implementation
The GA implemented in this work is as follows: Firstly, an initial population or randomly generated sequences of the tasks in the schedule are created. These individual schedules form chromosomes which are subjected to a form of Darwinian evolution. The fitness of each individual schedule in the population is calculated according to a user defined fitness function, such as makespan and completion time variance. The schedules are then ranked according to the value of their fitness. Two parents are selected from the current population using a rank based mechanism to control the probability of selection. These parents mate to produce a child solution by applying the crossover operator. Following crossover, the child may be mutated.
At this step, if precedence constraints have been defined in the model, and the child does not satisfy precedence constraints, it is modified as necessary to meet the precedence constraints. The child’s fitness is then calculated and it is added into the population. New child replaces the weakest schedule in the current pool or population of schedules. Selection, crossover and mutation operations are repeatedly performed until the fittest member of the evolving population converges to an optimal fitness value or the stopping criterion is reached.
5.1 Chromosome representation for alternative process plans
In this work, we use two different chromosome representations. First, a modified permutation representation is used. In this modified representation, all the possible operations (including the alternative operations) are included in the chromosome string. Thus, the chromosome representation introduced contains all the occurrences of alternative processes for a particular operation.
The chromosome representation is explained by the following example. Assume there are four jobs (A, B, C, D) to be performed on two identical parallel machines. A job can be performed on either of the two machines (1, 2), but it is not performed on both. Let A1 denote the processing of job A on machine 1, B2 the processing of job B on machine 2, etc. The chromosome to represent this schedule will contain eight jobs even though only four will actually be processed. Figure 2 gives an example of such a chromosome.
![]()
Fig. 2 First chromosome structure for alternative process plan
The chromosome in Fig. 2 says that jobs A, B and D are processed on machine 1 and job C is processed on machine 2. Each job actually appears twice but only the first occurrence is taken to be an ‘actual’ occurrence that must be included in the calculation of the fitness function while subsequent occurrences are ignored. However, all occurrences are included in the crossover and mutation so that jobs may change machines by reversing the order of the corresponding genes in the chromosome.
The second chromosome representation is shown in Fig. 3.

Fig. 3 Second chromosome structure for alternative process plan
This chromosome representation is explained as follows: there are three jobs each having two operations to be performed on three alternative machines. Each job can be performed on any one of the three machines. In Fig. 3, the first six genes i.e., from gene 1 to gene 6, represent the job-operation. A-1 means job A operation 1, A-2 means job A operation 2 and so on. The next six genes i.e., genes 7-12 are the machines associated with each job-operation. Genes 7-12 state that job A-1 is to be performed on machine 3, job B-1 on machine 1, job A-2 on machine 2, so and so forth.
For job-operation block, the order of the jobs is manipulated keeping in view the precedence constraints for each job-operation. They are linked to the machine assignment through the spreadsheet model to calculate the objective function value. For the order of jobs, i.e., first six genes order crossover is implemented while for machine assignment to jobs, i.e., last six genes, uniform crossover is implemented.
5.2 Selection
In Evolver?, parents are chosen using a rank-based mechanism. This procedure begins by rank ordering the population by fitness. Next, an assignment function gives each individual a probability of inclusion. The assignment function can be linear or nonlinear. A roulette wheel is then built with the slots determined by the assignment function. The next generation of an n-sized population is built by giving the wheel ‘n’ spins. This procedure guides selection towards the better performing members of the population but does not force any particular individual into the next generation.
5.3 Crossover operator
The crossover operator is an important component of GA. The crossover operation generates offspring from randomly selected pairs of individuals within the mating pool, by exchanging segments of the chromosome strings from the parents.
The order of jobs, i.e., first six genes, uses order crossover. DAVIS [40] developed this operator. This operator is based on using a bit string (zero-one) template to determine which parent will contribute to making the offspring. This fills some positions on offspring by copying the elements from P1 wherever the binary template contains “1” in the same position as they appear in P1. The elements from P1 associated with “0” in the template appear in the same order in the offspring as they appear in P2. An example is given in Table 1.
Table 1 Order-based crossover
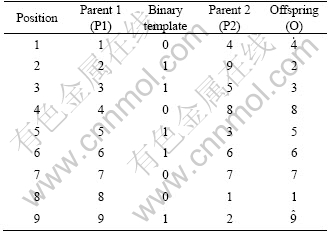
In Table 1, the elements associated with “1” in P1 are at position 2, 3, 5, 6 and 9 and are inherited by the offspring in the same positions. The remaining elements associated with “0” are 1, 4, 7 and 8. These elements appear in the same order in the offspring as they appear in P2.
For machine assignment, i.e., last six genes, uniform crossover operator is implemented. In uniform crossover operator, mixing ratio or crossover rate decides which parent will contribute each of the gene values in the offspring chromosome. This allows the parent chromosomes to be mixed at the gene level rather than the segment level. Consider the two parents in Fig. 4 which have been selected for crossover. Parent P1 has been coloured black grey while parent P2 bright grey. A random mask is generated corresponding to the crossover rate. If the crossover rate is 0.5, approximately half of the genes in the offspring will come from P1 and the other half will come from P2. Below the second parent is the random mask generated corresponding to the crossover rate. The child is produced by taking bit from P1 if the corresponding mask bit is 1 or the bit from P2 if the corresponding bit is 0. The colour of the child chromosome represents the mixing of genes if the crossover rate is 0.5.
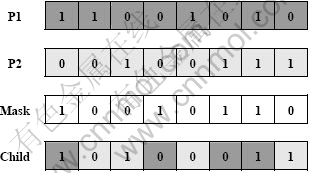
Fig. 4 Uniform crossover
5.4 Mutation operator
The purpose of the mutation is to ensure that diversity is maintained in the population. It gives random movement about the search space thus preventing the GA becoming trapped in ‘blind corners’ or ‘local optima’ during the search. Evolver? performs order-based mutation. In this mutation, two tasks are selected at random and their positions are swapped. The ‘mutation rate’ determines the probability that mutation is applied after a crossover. The number of swaps performed is increased or decreased proportionately with the increase and decrease in the mutation rate setting.
5.5 Reproduction
The worst performing organism is replaced with the new organism that is created by selection, crossover and mutation.
5.6 Precedence constraints
The precedence tasks for a particular job shop problem are specified in a table within the spreadsheet. It is a table of cells which describes which tasks must be preceded by other tasks. The proposed GA then uses this table to rearrange the order of variables in a scenario until the precedence constraints are met. Any chromosome that does not meet the precedence constraints is discarded and only solutions that meet the specified precedence constraints are kept in the population.
6 Job shop numerical example
We use the same example as in Ref. [1]. There are four jobs, and each has three different operations to be processed according to a given sequence. There are six different machines, and the alternative routing and processing times are given in Table 2.
In this example, operation 1 of job 1 i.e., O11 can be performed on machine 1, 2 or 3 (for 2, 3 or 4 units of time, respectively), operation 2 of job 1 i.e., O12 on machine 1, 2 or 3, and so on. Note, twenty three of these operations will not in fact be performed since they only represent the alternatives.
Table 2 Problem data [1]

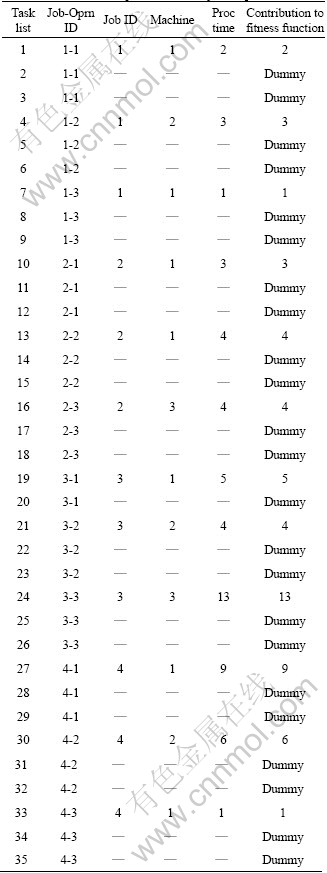
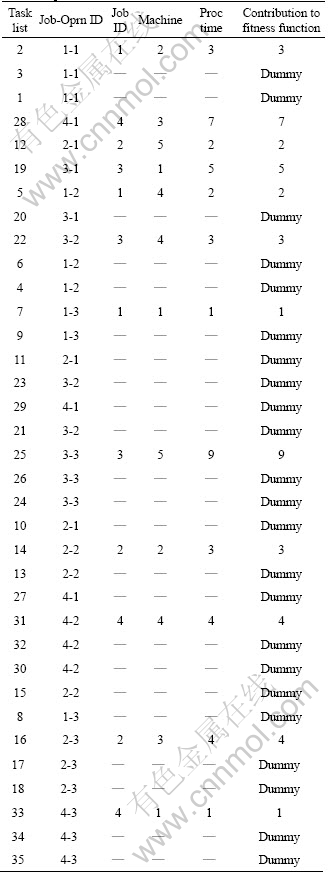
In Table 3, Job-Oprn ID of 1-1 would mean job 1 operation 1 and so on. The ‘Dummy’ mentioned in front of the operations means that although these operations are shown in the schedule but their contribution in the calculation of the objective function is zero.
We compare the results of the heuristic procedure of NASR and ELSAYED [1] with the GA application. NASR and ELSAYED’s heuristic found mean flow time of 12.25 with flow time of each job as 7, 11, 18 and 13, respectively. However, our GA application finds mean flow time of 11.75 with flow time of each job as 6, 11, 17 and 13, respectively. Repeated runs of the GA produced same solution. For this problem instance, the computational time on a 2.2 GHz Core Duo computer with 512 MB RAM was less than 10 s.
The resulting optimum schedule after running the GA is given in Table 4. As explained before, this is a sequence of thirty five operations.
It is instructive to observe how the GA has reversed the order of some of the alternative machine allocations. For example, tasks 4, 5 and 6 represent alternative operations for operation 2 of job 1. In the optimised schedule given in Table 3, the GA has taken the task list 5, so that tasks 4 and 6 have become a “dummy” gene in the chromosome. This example highlights the purpose of the duplicated “dummy” genes. Figure 5 shows the optimized job and machine schedule generated after the GA run.
For the second chromosome representation, the actual chromosome for the above mentioned problem can be seen in Fig. 6. The chromosome is read as follows: job 1-1 to be processed on machine 2, job 4-1 on machine 3, job 2-1 on machine 5, job 3-1 on machine 1, job 1-2 on machine 4, job 3-2 on machine 4, job 1-3 on machine 1, job 3-3 on machine 5, job 2-2 on machine 2, job 4-2 on machine 4, job 2-3 on machine 3 and job 4-3 on machine 1, respectively.
Table 3 Chromosome representation for job shop
For both the chromosome representations, the model was able to find the optimal solution in less than 10 s.
Table 4 Optimized schedule after GA run
7 Performance analysis of proposed approach
To illustrate the effectiveness of the proposed approach, several problems are tested. Their results are compared to results obtained by using other approaches.
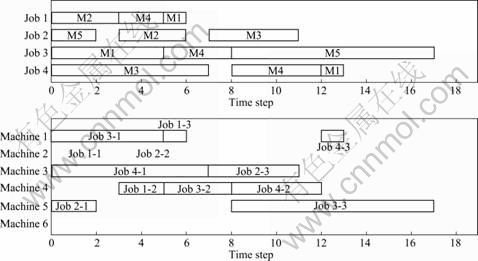
Fig. 5 Optimized job and machine schedule

Fig. 6 Actual chromosome for second representation
Example problem 2 is a five-part type, four-machine type problem, taken from Ref. [8]. Each part type has one part, each part has several alternative routings, and each machine type has one machine. Two different objectives, i.e. minimization of absolute deviation from due date and minimization of sum of the finishing times of all the jobs, are used for the problem. In both cases, the proposed GA produced the optimal solution within 5 s on a 2.2 GHz Core Duo computer with 512 MB RAM.
The critical observation to be made here is that it is simple to modify the basic GA to implement either of the objective functions considered above. In the first case, the fitness function is defined as the deviation from the due dates summed over all the jobs. In the second case, the objective function is the completion time summed over all the jobs. The GA simply performs these calculations after each crossover and mutation to yield the fitness of the new schedule. The formulation of the problem is far more complex than application specific when using the integer programming approach.
Third set of three problems is taken from Ref. [12]. The objective function to be minimized is the weighted quadratic tardiness. The optimization problem is
![]() (1)
(1)
where ωi is the weight of job Ai; Ti is the tardiness of job Ai.
The due dates of the jobs are set to the beginning of the planning period and the weight of the jobs to 1. The test data can be found in Ref. [12].
The first problem is a small example with three jobs and three operations each on three machines, which may process all of the operations, most of them at a different speed, i.e. all assignments are possible (3/3/3-example). The value for the sum of quadratic tardiness found by GA is 36 424, the Lagrange value found is 36 416.46, with an error of 0.02%. The sum of tardiness is 328 and optimal with respect to this criterion. GA in this work obtained the same solution within 3 s.
The second problem is an example with four jobs and four operations on three machines. They may process all of the operations, i.e. all assignments are possible (4/4/3-example). The sum of tardiness is 369 and optimal with respect to this criterion. The same solution was found within 20 s by the GA.
The third problem is an example with six jobs and ten operations each on six machines that may process almost all of the operations, most of them at a different speed, i.e. all assignments are possible (6/10/6-example). The best value of sum of tardiness found by GA is 1 557 which is better than the best value of 1 754 found in Ref. [41] and Ref. [12] with respect to this criterion.
The results for all the three problems are listed in Table 5. Table 6 gives the results with respect to sum of tardiness of the different methods including some priority rules for the examples [12, 41].
Table 5 Test results for comparison with Ref. [12]

Table 6 Sum of tardiness results for different methods [12, 41] and proposed GA

From Table 5, it can be seen that for example 1 and 2, proposed GA and heuristic approach produced the same solution for the sum of quadratic tardiness. However, Lagrange approach produced 2.65% better solution as compared to the GA approach. The rest of the values are same for all the three approaches. The computation time for GA (with population size of 65, crossover probability of 0.65 and mutation rate of 0.01) was 5 and 20 s for example 1 and 2, respectively. For example 3, GA consistently produced better solution as compared to Heuristic and Lagrange approach. GA produced 9.18% and 4.50% better solution as compared to Heuristic and Lagrange approach, respectively. For all other parameters, also GA produced better solution, while the computation time for the solution was 2 min on a 2.2 GHz Core Duo computer with 512 MB RAM. In Table 6, the solution values have not been reported [12] for Exact B & B. Similarly, the optimal value for the problem is also not known.
The fourth problem set is taken from Ref. [24]. They obtained information from an electrical motor factory and used the GA to find the optimal makespan. In workshop, there are twelve jobs and nine machines which are grouped by six work centers. The first five jobs are heavier than (have long process times) other jobs. Forward Scheduling (FS) was previously being used in the mentioned workshop, so that heavy jobs are first processed on Work Center A, B, …, F sequentially.
In work center A, machine 1 has been purchased recently and its performance is higher than the other machines (machine 2 and 3). As for work center B, machine 4 handles the same operation more quickly than machine 5. Work center based operation sequences and process times of twelve jobs can be found in Ref. [24]. A makespan time of 336 min is obtained by the GA approach in this work. However, according to FS method that is currently used in factory and the GA by BASKAK and EROL, all machines process their work in 474 and 374 min, respectively, which is an improvement of 29% over FS approach and 10% over BASKAK and EROL’s GA. A comparative analysis of the three approaches is given in Table 7. GA found this solution within 1 min on a 2.2 GHz Core Duo computer with 512 MB RAM.
The fifth problem set is taken from Ref. [42]. It consists of a job shop scheduling problem with five parts while each part has four operations. Some of the operations have more than one machine to process that operation. The problem is to find a schedule, specifying the machines to perform each operation on parts with the objective of minimizing makespan, or the time required to complete all operations. Using the GA-based method, the best value obtained is 33 within 10 s as compared with the value of 38 obtained using the heuristic reported by SUNDARAM and FU [42]. Same value of 33 was also obtained by MORAD and ZALZALA [43] using genetic algorithms and by PALMER [44] using simulated annealing.
To further illustrate the effectiveness and performance of our proposed GA approach, we selected five representable instances (represented by problem n×m, where n is the number of jobs while m is the number of machines) from the literature. These instances have been used by many researchers. Five problem instances (problem 4×5, problem 8×8, problem 10×7, problem 10×10 and problem 15×10) are all taken from Ref. [45]. We applied the proposed GA approach to the five instances.
The proposed GA approach is compared with earlier reported studies, i.e., simulation model by XING et al [46], ‘PSO+SA’ by XIA and WU [47], ‘AL+CGA’, ‘Approach by Localization’, ‘Controlled GA’ and ‘Temporal Decomposition’ all by KACEM et al [45], ‘Heuristic SPT’ and moGA by ZHANG and GEN [48]. The comparative results of all of the above mentioned approaches and the proposed GA approach are tabulated in Table 8. The objective function, F, used in all the five instances is the weighted sum of three objectives as
given by
F=0.5×F1+0.2×F2+0.3F3 (2)
where F1 is the makespan or maximal completion time of machines; F2 is the total workload of machines, which represents the total working time on all machines; F3 is the critical machine workload, which is the machine with the biggest workload.
Table 7 Comparative analysis of three approaches
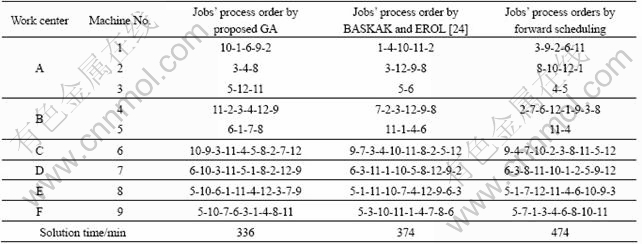
Table 8 Comparison of proposed GA approach with various previous solution methods
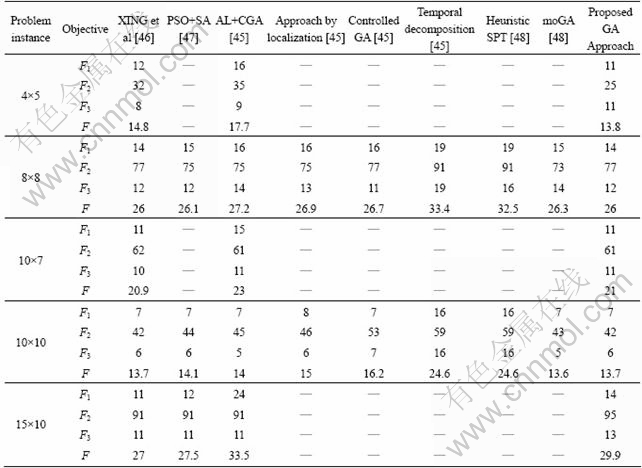
Instance 1 (small size, 4 jobs / 12 operations / 5 machines) is an instance of total flexibility i.e., each of the operation of the four jobs can be processed on any of the five machines. From Table 8, we can see that the proposed GA approach produced better solutions as compared to the previously reported approaches i.e., simulation model by XING et al [46] and ‘AL+CGA’ [45].
Instance 2 (medium size, 8 jobs / 27 operations / 8 machines) is an instance of partial flexibility, i.e., some operations are only available on a part of the available machines set. In this case, the proposed GA approach produced same solution as obtained by simulation model by XING et al [46], while it produced better solution than ‘PSO+SA’ [47], ‘AL+CGA’ [45], ‘Approach by localization’ [45], ‘Controlled GA’ [45] and ‘Temporal decomposition’ [45], ‘Heuristic SPT’ [48] and moGA [48].
Instance 3 (medium size, 10 jobs / 29 operations / 7 machines) is an instance of total flexibility. Proposed GA approach produced better solution than AL+CGA’ [45], while XING et al’s [46] solution was only 0.48% better.
Instance 4 (medium size, 10 jobs / 30 operations / 10 machines) is also a case of total flexibility. Proposed GA approach produced same solution as obtained by XING et al [46]. However, moGA [48] marginally produced a better solution than both XING et al [46] and the proposed GA approach, while the proposed approach produced better solution as compared to the rest of the approaches.
Instance 5 (large size, 15 jobs / 56 operations / 10 machines), is also a case of total flexibility. The proposed GA solution was better as compared to AL+CGA’ [45] only, while as compared to XING et al [46] and ‘PSO+SA’ [47], the obtained solution was worse.
8 Conclusions
1) It has been shown that GA can be used to optimise schedules with alternative routes/machines. The application of the approach has been demonstrated by a job shop example. Performance analysis of the proposed approach is evaluated by testing it on the job shop problems taken from the literature. The results obtained are competitive to those achieved by previously reported methods, but without the need for complex customisation to meet the needs of a particular situation.
2) A modified permutation chromosome representation for schedules with alternative machines for given operations has been presented. Although all the alternatives are included in the chromosome, the second and subsequent appearances of an operation in the chromosome do not contribute to the overall calculation of the fitness value. However, all occurrences are included in the crossover and mutation operations, allowing for alternatives. This chromosome representation does not represent a customisation of the GA method to accommodate a particular problem. Instead, it is a generalisation of the existing representation, which in turn becomes a reduced form of this generalised form. However, the second chromosome representation also produces the same results as the modified permutation representation.
3) Spreadsheets have a natural interface that exists for model building, the ease of use in terms of inputs, solutions and report generation, and ability to perform “what-if” analysis. Therefore, the spreadsheet based approach makes it easier for a decision maker to perform ‘what-if’ analysis.
4) It must be noted that, in practice, not every machine can process each operation. In reality, there exist at most two to three alternative machines per operation that may replace each other, as the cost for this redundancy would be enormous. This reduces the assignments to be examined and the fine tuning of the multipliers a lot. Accordingly, the expected computational effort will be reduced. These most general examples were investigated to show the ability of the method in principle even for this extreme case and to demonstrate the quality of the results.
References
[1] NASR N, ELSAYED E A. Job shop scheduling with alternative machines [J]. International Journal of Production Research, 1990, 28(9): 1595-1609.
[2] NSAR N. Scheduling of production systems with flexible routings [C]// Proceedings of the Second Industrial Engineering Research Conference. Los Angeles, CA, USA, 1992: 487-492.
[3] WILHELM W, SHIN H. Effectiveness of alternative operations in a flexible manufacturing system [J]. International Journal of Production Research, 1985, 23(1): 65-79.
[4] HANKINS S L, WYSK R A, FOX K R. Using a CATS database for alternative machine loading [J]. Journal of Manufacturing Systems, 1984, 3: 115-120.
[5] AHN J, HE W, KUSIAK A. Scheduling with alternative operations [J]. IEEE Transactions on Robotics & Automation, 1993, 9(3): 297-303.
[6] KIM K H, EGBELU P J. Scheduling in a production environment with multiple process plans per job [J]. International Journal of Production Research, 1999, 37(12): 2725-2753.
[7] RAJAMANI D, SINGH N, ANEJA Y P. Integrated design of cellular manufacturing systems in the presence of alternative process plans [J]. International Journal of Production Research, 1990, 28(8): 1541-1554.
[8] JIANG J, HSIAO W. Mathematical programming for the scheduling problem with alternative process plans in FMS [J]. Computer & Industrial Engineering, 1994, 27(1-4): 15-18.
[9] KIM K H, EGBELU P J. A mathematical model for job shop scheduling with multiple process plan consideration per job [J]. Production Planning & Control, 1998, 9: 250-259.
[10] CHOI I C, CHOI D S. A local search algorithm for job shop scheduling problems with alternative operations and sequence- dependent setups [J]. Computers & Industrial Engineering, 2002, 42(1): 43-58.
[11] CHEN J S, PAN J C H. Minimising mean tardiness with alternative operations in two-machine flow-shop scheduling [J]. International Journal of Systems Science, 2005, 36(12): 757-766.
[12] THOMALLA C S. Job shop scheduling with alternative process plans [J]. International Journal of Production Economics, 2001, 74(1): 125-134.
[13] DAUZ?RE-P?R?S S, PAULLI J. An integrated approach for modeling and solving the general multiprocessor job-shop scheduling [J]. Annals of Operations Research, 1997, 70(3): 281-306.
[14] LOGENDRAN R, SONTHINEN A. A Tabu search-based approach for scheduling job-shop type flexible manufacturing systems [J]. Journal of Operational Research Society, 1997, 48(3): 264-277.
[15] BILGE ?, KIRA? F, KURTULAN M, PEKG?N P. A tabu search algorithm for parallel machine total tardiness problem [J]. Computers & Operations Research, 2004, 31(3): 397-414.
[16] SCRICH C R, ARMENTANO V A, LAGUNA M. Tardiness minimization in a flexible job shop: A tabu search approach [J]. Journal of Intelligent Manufacturing, 2004, 15(1): 103-115.
[17] CAO D, CHEN M, WAN G. Parallel machine selection and job scheduling to minimize machine cost and job tardiness [J]. Computers & Operations Research, 2005, 32(8): 1995-2012.
[18] MEHRABAD M S, FATTAHI P. Flexible job shop scheduling with tabu search algorithms [J]. International Journal of Advanced Manufacturing Technology, 2007, 32(5/6): 563-570.
[19] CANDIDO M A B, KHATOR S K, BARCIA R M. A genetic algorithm based procedure for more realistic job shop scheduling problems [J]. International Journal of Production Research, 1998, 36(12): 3437-3457.
[20] ZHAO C, WU Z. A genetic algorithm approach to the scheduling of FMSs with multiple routes [J]. International Journal of Flexible Manufacturing Systems, 2001, 13(1): 71-88.
[21] ROSSI A, DINI G. An evolutionary approach to complex job-shop and flexible manufacturing system scheduling [J]. Journal of Engineering Manufacture, 2001, 215(2): 233-245.
[22] KIM Y K, PARK K, KO J. A symbiotic evolutionary algorithm for the integration of process planning and job shop scheduling [J]. Computers & Operations Research, 2003, 30(8): 1151-1171.
[23] TAVAKKOLI-MOGHADDAM R, KHODADADEGHAN Y, HAGHNEVIS M. Efficient algorithm for a multi-criteria parallel machine scheduling problem with sequence-dependent setup times [C]// Proceedings of 5th International Symposium on Intelligent Manufacturing Systems. Sakarya, Turkey: Sakarya University, 2006: 159-167.
[24] BASKAK M, EROL V A. Genetic algorithm approach for solving flexible job-shop scheduling problem [C]// Proceedings of 35th International Conference on Computers & Industrial Engineering. Istanbul, Turkey, 2005: 245-250.
[25] HUSSAIN M F, JOSHI S B. A genetic algorithm for job shop scheduling problems with alternate routing [C]// IEEE International Conference on Systems, Man and Cybernetics. San Diego, CA, USA, 1998: 2225-2230.
[26] JAWAHAR N, ARAVINDAN P, PONNAMBALAM S G. A genetic algorithm for scheduling flexible manufacturing systems [J]. International Journal of Advanced Manufacturing Technology, 1998, 14(8): 588-607.
[27] BECK J C, FOX M S. Constraint-directed techniques for scheduling alternative activities [J]. Artificial Intelligence, 2000, 121(1/2): 211-250.
[28] FERREIRA J C E, WYSK R A. On the efficiency of alternatives in process plans [J]. Journal of Brazilian Society of Mechanical Sciences, 2001, 23(3): 303-319.
[29] SAYGIN C, CHEN F F, SINGH J. Real-time manipulation of alternative routings in flexible manufacturing systems: A simulation study [J]. International Journal of Advanced Manufacturing Technology, 2001, 18(10): 755-763.
[30] DEMIR H I. Scheduling with alternative routes [C]// Proceedings of 5th International Symposium on Intelligent Manufacturing Systems. Sakarya, Turkey: Sakarya University, 2006: 1323-1338.
[31] ROSSI A, DINI G. Flexible job-shop scheduling with routing flexibility and separable setup times using ant colony optimisation method [J]. Robotics & Computer Integrated Manufacturing, 2007, 23(5): 503-516.
[32] LOW C, HSU C J, SU C T. A two-stage hybrid flowshop scheduling problem with a function constraint and unrelated alternative machines [J]. Computers & Operations Research, 2008, 35(3): 845-853.
[33] HOLLAND J. Adaptation in natural and artificial systems [M]. Ann Arbor: University of Michigan Press, 1975.
[34] GOLDBERG D E. Genetic algorithms in search, optimization and machine learning [M]. New York: Addison-Wesley Publishing Company, 1989.
[35] DAVIS L. Job shop scheduling with genetic algorithms [C]// GREFENSTETTE J J. Proceedings of the 1st International Conference on Genetic Algorithms. Hillsdale, NJ: Lawrence Erlbaum, 1985: 136-140.
[36] CHAUDHRY I A, DRAKE P R. Minimizing flow time variance in a single machine system using genetic algorithms [J]. International Journal of Advanced Manufacturing Technology, 2008, 39(3/4): 355-366.
[37] CHAUDHRY I A, Drake P R. Minimizing total tardiness for the machine scheduling and worker assignment problems in identical parallel machines using genetic algorithms [J]. International Journal of Advanced Manufacturing Technology, 2009, 42(5/6): 581-594.
[38] CHAUDHRY I A. Minimizing flow time for the worker assignment problem in identical parallel machine models using GA [J]. International Journal of Advanced Manufacturing Technology, 2009, 48(5-8): 747-760.
[39] Palisade Corp. Genetic algorithm solver for Microsoft Excel: Guide to evolver [M]. New York: Palisade corporation, 1998.
[40] DAVIS L. Handbook of genetic algorithms [M]. New York: Van Nostrand Reinhold, 1991: 332-349.
[41] MUELLER K. Development, implementation and test of a heuristic branch-and-bound procedure for machine assignment in flexible manufacturing system [D]. Diplomarbeit, Universitat Karlsruhe, Fakultat fur Informatik, 1992. (in German).
[42] SUNDARAM R M, FU S S. Process planning and scheduling—A method of integration for productivity improvement [J]. Computers & Industrial Engineering, 1998, 15(1-4): 296-301.
[43] MORAD N, ZALZALA A M S. Genetic algorithms in integrated process planning and scheduling [J]. Journal of Intelligent Manufacturing, 1999, 10(2): 169-179.
[44] PALMER G. J. A simulated annealing approach to integrated production scheduling [J]. Journal of Intelligent Manufacturing, 1996, 7(3): 163-176.
[45] KACEM I, HAMMADI S, BORNE P. Approach by localization and multi-objective evolutionary optimization for flexible job-shop scheduling problems [J]. IEEE Transactions on Systems, Man & Cybernetics, Part C, 2002, 32(1): 1-13.
[46] XING L N, CHEN Y W, YANG K W. Multi-objective flexible job shop schedule: Design and evaluation by simulation modelling [J]. Applied Soft Computing, 2009, 9(1): 362-376.
[47] XIA W, WU Z. An effective hybrid optimization approach for multi-objective flexible job-shop scheduling problems [J]. Computers & Industrial Engineering, 2005, 48(3): 409-425.
[48] ZHANG H, GEN M. Multistage-based genetic algorithm for flexible job-shop scheduling problem [J]. Journal of Complexity International, 2005, 11: 223-232.
(Edited by YANG Bing)
Received date: 2011-04-23; Accepted date: 2011-07-14
Corresponding author: I. A. Chaudhry, PhD; Tel: +92-300-4279895; E-mail: imran_chaudhry@yahoo.com

