随机跳频压缩感知雷达动态高分辨距离成像
游鹏，刘振，泰玉亮，王宏强，黎湘
(国防科技大学 电子科学与工程学院，湖南 长沙，410073)
摘要：针对实际中难以事先确定随机跳频压缩感知雷达所需脉冲数的问题，设计一种高分辨距离像动态合成策略。该策略的核心是序贯发射和接收跳频脉冲，同时用接收数据序贯更新对目标距离像的估计，直至满足设定的停止条件为止。为实现快速序贯更新，提出一种高效的复数域同伦算法。该算法实现快速递归稀疏恢复，避免每次加入一个新的观测时都要求解一个新的优化问题。此外，利用距离像的相关性特征，给出一种合理的停止准则。研究结果表明：采用所提出的动态合成策略，能够利用雷达回波信号自适应地确定最优脉冲数，在非合作运动目标成像方面具有显著优势。
关键词：高分辨距离像；随机跳频；压缩感知；复数值同伦；递归稀疏恢复
中图分类号: TN95 文献标志码：A 文章编号：1672-7207(2014)04-1119-09
Dynamic HRRP generation for random frequency-hopping compressive sensing radar
YOU Peng, LIU Zhen, QIN Yuliang, WANG Hongqiang, LI Xiang
(School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)
Abstract: Considering that the required pulse number was difficult to determine in advance for random frequency-hopping (RFH) compressive sensing radar, a dynamic synthesis strategy for high resolution range profile (HRRP) generation was proposed, whose core was to sequentially transmit and receive pulses, and to update the HRRP with the sequential received pulses until a proper stopping rule was satisfied. To efficiently implement the sequential update, a fast complex-valued homotopy algorithm was developed. This algorithm performs as an efficient recursive procedure of sparse recovery, thus avoids solving a new optimization problem from scratch. Furthermore, the proper stopping rule was given according to the correlation characteristics of HRRP. The results show that the optimal pulse number required in each CPI can be sought to adapt to the echo signal, and the established dynamic approach is more suitable for uncooperative moving targets.
Key words: high resolution range profile(HRRP); random frequency-hopping(RFH); compressive sensing(CS); complex-valued homotopy; recursive sparse recovery
获取目标的高分辨距离像(high resolution range profile，HRRP)需要发射大时宽带宽信号。与发射线性调频信号(linear frequency modulated，LFM)这样的大瞬时带宽信号相比，发射步进频率波形对雷达硬件的要求更低，通过发射多个步进频率波形可以合成大带宽进而获得目标的高分辨距离像[1]。然而，由于需要发射多个脉冲以覆盖大带宽，步进频率体制雷达往往难以在脉冲重复频率(pulse repetition frequency，PRF)和相干积累时间(coherent processing interval，CPI)两方面取得合理折中。一方面，对于固定的低和中PRF，雷达需要较长的观测时间以覆盖所需带宽。这不但限制了雷达同时段完成多种任务、监视多个目标的能力，而且加大了对非合作运动目标回波脉冲相干积累的难度，极有可能导致成像质量下降甚至无法成像。另一方面，对于固定的相干积累时间，发射多个脉冲需要的高PRF将带来严重的距离模糊和盲区效应。与线性步进频率雷达相比，稀疏随机跳频(random frequency hopping，RFH)[2-3]雷达需要发射的脉冲数更少，有望在保留前者优势的同时部分或者完全克服其根本缺陷。然而，采用传统的相关方法处理稀疏随机跳频信号的回波存在高旁瓣问题，严重影响成像质量。为了克服这一问题，CLEAN方法可用于获得高质量的目标图像[4]。这种高分辨方法本质上是一种求稀疏解方法[5]，可以看作匹配追踪的一种实现形式[6]。近年来，随着稀疏恢复方法的快速发展[7]，特别是在压缩感知(compressive sensing，CS)理论[8-9]的推动下，利用目标图像的稀疏先验信息实现随机跳频雷达的高分辨成像已成为研究热点[10-12]。尽管压缩感知理论给出了准确重构所需脉冲数的估计，但是，由于事先无法获知目标的稀疏度，因此，难以根据理论确定所需脉冲数。若为了保守起见而选择1个较大的数，则不但增加了不必要的发射，浪费雷达资源，而且可能受目标非合作运动的影响而降低成像质量。为了既满足成像要求又尽可能减少脉冲数，本文作者设计一种高分辨距离像动态合成策略。该策略的核心思想是序贯的发射和接收跳频脉冲，同时对距离像进行序贯估计，直至停止条件得到满足为止。为了实现快速的序贯估计以满足实时更新的要求，将实数域快速序贯同伦(fast sequential homotopy，FSH)[13]推广至复数域，提出一种高效的复数域快速序贯同伦算法。该算法实现了递归稀疏恢复，避免了每次加入一个新的观测时都要求解一个新的优化问题。此外，根据一维距离像的相关性特征给出停止准则。通过采用这一动态合成策略可以获得自适应雷达回波的最优脉冲数。
1 信号模型和高分辨距离像动态合成策略
1.1 随机跳频雷达信号模型
随机跳频脉冲串信号模型如图1所示。随机跳频雷达的脉冲串信号由M个频率脉冲组成，其中脉冲数M需要根据不同的场景加以确定。第m个脉冲的载频为Fm=fc+fm(其中，fc为中心频率，fm=Cm△f为带宽B内随机分布的频率，△f为对应线性步进频率信号的频率步进间隔)。设脉冲重复时间为Tr，脉冲宽度为T。并假设目标包含K个散射中心，第k个散射中心的散射系数为Ak，与雷达的初始距离为R0k。另假设目标以速度v作匀速运动，则经过下变频和低通滤波后的回波信号可以表示为
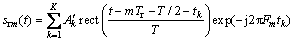(1)
其中：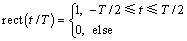
；m=0，1，…，M-1；
为回波包络；t为时间变量；
；t0k为初始时刻的时延；tk为目标瞬时距离对应的时延。在
时刻对信号进行采样(其中，
，
为采样时刻对应的目标附近某点到雷达的距离，
为初始时刻目标距离对应的时延)，则输出信号可以表示为
(2)
考虑将不模糊时延(对应脉冲重复时间)Tr划分为N个等间隔分布的点，表示为
(其中，
；△t为时延分辨单元；n=0，1，…，N-1)。同理，也将速度所在的区间划分为L个等间隔分布的点，表示为
(其中，△t为速度划分间隔，vc为目标初始速度；l=0，1，…，L-1)。因此，在噪声条件下(2)可以表示为
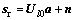(3)
其中：Ul0为M×N随机矩阵；其中元素为
；Vl0=v。向量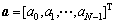
为所需重构的高分辨距离像，其稀疏性表现为只有
个非零元素或者幅度较大的元素，它们对应目标的少量散射中心；n为零均值观测噪声向量。
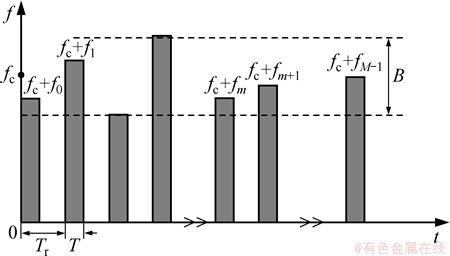
图1 随机跳频脉冲串信号模型
Fig. 1 Pulse train signal model of RFH
1.2 高分辨距离像动态合成策略
观测方程(3)可以看作为一个典型的不定线性方程组。由于发射的是随机载频脉冲串，式(3)对应的观测矩阵乃是随机采样亚傅里叶矩阵，满足CS所需的压缩等距(RIP)条件[14]。在高信噪比以及目标包含的散射中心数充分小于距离分辨单元数的条件下，脉冲个数满足如下条件即可保证准确重构距离像信号[15]：
(4)
若脉冲数满足条件(4)，则根据观测方程(3)，高分辨距离像可以通过求解以下优化模型来准确重构：
(5)
其中：λ为正则化参数。然而，在实际中，目标等效的散射中心数会因为目标以及目标姿态等不同而发生变化，因此，难以利用理论结果事先确定所需要发射的脉冲数。为了既满足成像要求又尽可能减少脉冲数，引入动态压缩感知的思想[16]。与传统处理过程中等待收集到所有的脉冲回波后一次性处理不同，可以首先处理少量脉冲的回波得到HRRP的初始值，然后，在得到新的脉冲回波时对HRRP进行序贯更新，直到获得令人满意的HRRP或达到最大脉冲个数为止。在这种情况下，可以充分利用脉冲之间的时间间隔，使用快速的序贯处理方法。HRRP合成与运动补偿的动态策略流程如图2所示，其具体步骤如下。
初始化：设定脉冲个数为M=Mmin，利用跟踪系统得到的粗速度估计值为vc。
第1步：通过求解下面的基追踪去噪(basis pursuit denoising，BPDN)问题得到第l个速度单元对应的HRRP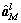
，
(6)
其中：
为M×V维的随机感知矩阵；
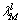为对应的正则化参数。
第2步：利用最小l1范数准则得到HRRP和速度估计值。
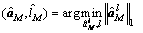(7)
其中：
为M个脉冲条件下的HRRP；
为相应的速度单元估计值。
第3步：当得到第M+1个回波的采样值Sr[M+1]后，有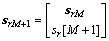
。设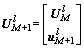
，
，为获得第M+1个回波的观测投影向量。利用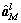，和作为初始值求解下面的问题重新估计
，
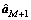和
。
(8)
(9)
第4步：若在第M+1个脉冲时所得到的HRRP和速度单元估计值与第M个脉冲时足够相似，或者脉冲数达到最大值，即M+1=Mmax，那么，在第3步中得到的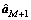就是最终的HRRP，对应目标速度的最终估计值
；否则，令M=M+1，
，
，
，
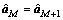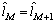，然后转到第3步。
图2 基于RFH雷达的动态HRRP合成处理流程图
Fig. 2 Flow chart of dynamic HRRP synthesis processing for RFH radar
2 快速序贯更新的复数同伦算法
要实现以上高分辨距离像动态合成策略，关键是解决2个重要问题：
一个是如何避免每次加入一个新的观测时都要求解一个新的优化问题，实现快速序贯更新。尽管有些稀疏恢复算法(如梯度投影稀疏重构[17])可以利用上一次的结果作为当前的初值来降低计算量，但最近出现的实数域快速序贯同伦算法[13]已被证实在噪声情况下更为有效，因此，这里将该算法扩展到复数域，用来实现HRRP的快速序贯更新。
另一个是需要针对特殊的应用场景设计合理的停止准则，从而得到所需要的最少脉冲个数。
同伦算法[18]是一种高效的稀疏恢复算法，其参数设置相对比较简单。这里首先假设式(6)中的BPDN问题已经用同伦方法成功求解，通过改进FSH算法更有效地求解式(8)。在FSH算法中，通过对同伦算法进行改进，可以在实数域序贯获取新的观测值时实时高效地更新原有的求解。
2.1 复数域到实数域的转换
为了使得推导更为简单，重新考虑抽象的复数域信号模型及相应的BPDN问题：
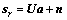(10)
(11)
其中：
，为等效的感知矩阵；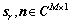
，分别为测量和噪声向量；
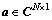，为稀疏向量；λ为正则化参数。为了使用实数域的稀疏恢复算法，将模型转换为实数域的模型：
(12)
(13)
于是，式(10)和式(11)可以近似等价为
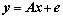(14)
(15)
2.2 复数域模型的FSH
这里将FSH算法从实数域推广到复数域。假设利用现有的观测数据已经求解式(15)并得到估计x0以及a0(
)，并得到相应的λ。现在又有了新的观测值
(其中，
为新的观测对应的感知向量，
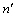为新观测中的复数噪声)。类似地，对应的实数模型可以写成
(16)
这实际上可以近似看作是序贯加入2个实数观测，因此，首先考虑加入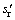
的实部。定义
，
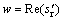以及
，则新的线性系统可以表示为
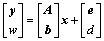(17)
于是，需要求解与式(8)类似的更新问题：
(18)
通过引入参数ε，新的观测可以逐渐加入到模型中[13]。
(19)
当ε从0变化到1时，已经求解的式(15)逐渐转变为式(18)。根据FSH算法，可以利用同伦思想更新求解。为了加入观测的虚部，可以用同样的思路，在式(17)中，令
(20)
(21)
(22)
通过再次使用FSH算法可以得到最终x和a的估计。表1所示为复数域FSH算法的具体实现流程。
表1 复数域FSH算法的具体实现流程
Table 1 Complex-valued FSH algorithm
3 停止准则
在上述动态算法的基础上，只要能够根据HRRP的特殊性质定义合适的停止准则，就可以根据目标回波信号动态确定所需要的最少脉冲个数。基于CS的算法其收敛性主要建立在下面2个条件的基础上：一方面，观测数越多则恢复性能越好，若某一时刻恰好处于满足RIP条件的临界点，则即使多1个观测值也可能导致恢复结果从错误变为正确；另一方面，由于增加1个脉冲不会给CPI带来较大的变化，因此，若已经得到正确的目标速度与HRRP，则增加1个观测值后恢复得到的目标速度和HRRP幅度特性的变化也往往可以忽略。鉴于这2点，可以通过2次相邻结果的“一步吻合”特性来定义终止准则。
显然，算法终止的一个必要条件是相邻2次得到的目标径向速度估计值相同，也就是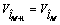
，这保证了运动补偿的正确性；另一个终止准则可以设定为2个相邻HRRP的相似性足够大。假定某种场景下感知矩阵满足RIP条件所需要的最少脉冲个数为Mopt，可以预计，当
时，由于CS算法产生的随机性误差，2个相邻HRRP的相似性较小；而当
时，2个相邻的HRRP应该较吻合。因此，可以利用第M个和第M+1个脉冲时得到的HRRP的归一化相关系数
(28)
来估计最优的脉冲个数Mopt。其中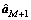，分别为利用M和M+1个脉冲重构的HRRP。若相关系数小于某个合适的门限cth，0＜＜cth＜1，则需要增大M，即新发射1个脉冲；相反，若相关系数大于cth，则表示已经得到正确的HRRP，动态算法可以终止。
所提动态算法的终止条件为：(1) 脉冲个数超过预先设定的范围；(2) 当前的速度估计值与上一次的相同；(3) 当前的HRRP与上一次的HRRP之间的归一化相关系数足够大。
4 实验及结果分析
利用仿真和暗室数据验证复数值序贯同伦算法和高分辨距离像动态合成策略的有效性。仿真平台为：奔腾4的3.00 GHz 微处理器(CPU)；1 GB内存；Windows XP操作系统；Matlab 7数值计算软件。
4.1 复数域FSH的有效性
首先利用理想散射中心模型验证复数域FSH算法的有效性。假设所发射的RFH信号参数如下：脉冲载频分布在9.5~10.5 GHz，脉冲重复时间Tr=100 μs，脉宽T=0.1 μs，因此，时延分辨单元△t=1 ns，时延分辨单元数N=100。假设目标的散射点个数K分别为20和30，它们所对应回波幅度的实部和虚部都服从随机正态分布N(0,12)，且分布在雷达视线方向的范围为15 m。目标距离雷达的距离为6 km，且假设目标静止。最小和最大的发射脉冲个数分别设定为30和90。当检测到目标后，发射RFH信号对目标进行HRRP成像，观测高斯白噪声的实部和虚部分别服从随机正态分布N(0,0.012)。为了比较，分别采用复数域FSH、直接同伦算法和凸(convex,CVX)优化工具箱[19]中的基追踪算法(简称CVX算法)进行处理，蒙特卡洛仿真次数设为200。
对每一次更新，都计算真实场景与恢复场景的平均归一化相关系数(average normalized correlation coefficients，ANCC)。如图3(a)所示，所有3种算法下ANCC都随着脉冲个数的增加而快速增大，且当脉冲个数足够大时都趋向于接近1的常数；随着脉冲个数的增加和散射点个数的减少，RIP条件逐渐得到满足，采用稀疏恢复算法也可以得到精确的参数估计。对于精度较高的CVX算法，其性能相对优于直接同伦和FSH算法。而直接同伦与FSH的结果除了运行时间不同外其余几乎完全相同。
图3(b)所示给出了3种算法的平均运行时间。从图3(b)可以看出：CVX算法对应的运行时间最长，而直接同伦算法由于每次都要求解较大维数的优化算法，运行时间相对也比较稳定；对于FSH算法，随着脉冲个数的增多，算法的运行时间基本保持不变且比直接同伦算法的运行时间有所降低，在脉冲个数足够多、恢复结果相对稳定时甚至降低更多。另外，对于少的目标散射点，其对应的运行时间也较少。因此，综合考虑计算量和恢复性能，FSH算法更适合快速序贯处理。
4.2 静止目标的序贯HRRP合成
在验证动态合成策略的可行性之前，先针对图4(a)中的静止目标利用FSH算法实现HRRP的序贯生成。采用频率步进方式，测量9~11 GHz(步进间隔为20 MHz)下目标的雷达散射截面(radar cross section，RCS)数据。目标的方位角范围为0°~90°(间隔为1°)。对每个方位角的100个采样数据进行128点的稀疏恢复，可以得到所有450个HRRP，如图4(b)所示。将使用全部数据获得的HRRP称为原始HRRP，在后面的分析中用作参考。
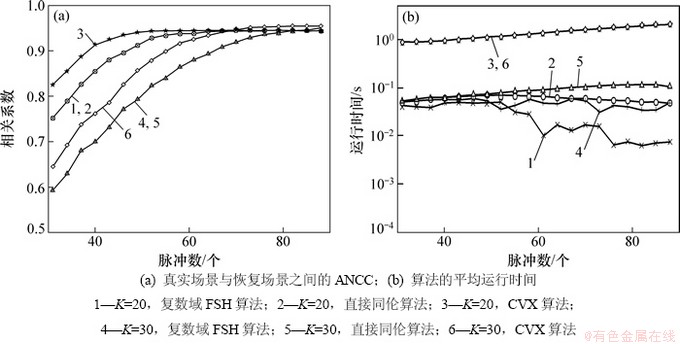
图3 不同算法及散射点个数条件下HRRP的合成性能
Fig. 3 HRRP generation performance of different algorithms with various numbers of scattering centers
图4 目标模型及其HRRP序列
Fig. 4 Model of target and its HRRP sequence
同样，从频率步进雷达的100个采样点中随机抽取M个(从16个增加到64个)来模拟RFH雷达的回波采样数据。由于抽取是随机的，因此，需要验证该方法的可重复性。为此，选择2个典型方位(5°和45°)，对每个方位进行200次蒙特卡洛仿真来确定最佳测量数。首先，分别给出2个不同方位角下的目标HRRP(见图5(a)和5(b))，很明显，45°方位角时的HRRP比5°方位角下的HRRP包含的强散射点个数少。随后，利用复数域的FSH算法对数据进行处理。图5(c)和图5(d)所示分别为2个方位角下相邻HRRP之间的ANCC随观测数据个数的变化。为了对比，同时给出了恢复HRRP与原始HRRP之间的ANCC。从图5可以看出：在方位角为5°和观测数据个数大于50时，HRRP趋于稳定，此时恢复HRRP与原始HRRP之间的ANCC大于0.95，而相邻HRRP之间的ANCC总是大于0.99。因此，可以将50看作是最合适的测量数据个数。当方位角为45°时，由于散射点个数较少，最合适的测量个数约为24。通过仿真结果可以得出：当测量数据个数足够多时，可以利用比传统意义上少得多的观测数据得到精确的HRRP。这是因为当观测数据个数多到可以满足RIP条件时，基于CS算法得到的结果基本不变。
为了进一步验证终止准则的有效性，对所有方位角下的数据进行处理得出合适的测量数据个数。测量个数的范围设定为16~80，终止条件为相邻HRRP之间的ANCC大于0.99。图6(a)所示为原始HRRP序列中包含主要散射点区域的局部放大图，图6(b)所示则反映相应的最合适观测数据个数。从图6可以看到：随着方位角的增大，目标在雷达视线上的强散射中心个数有逐渐减少的变化趋势，而所得到的最合适测量数据个数也有相应的趋势，因此，可以认为所需测量数据个数与目标强散射点数之间近似为正比关系，这与RIP条件是吻合的。
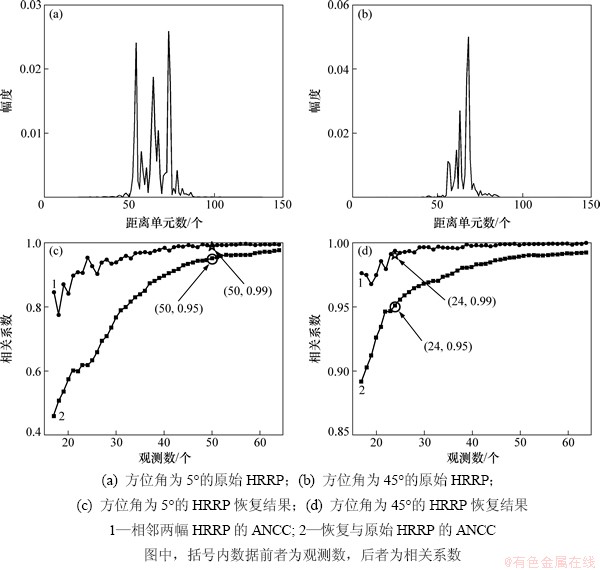
图5 基于动态合成策略的静止目标HRRP合成结果
Fig. 5 Results of dynamic synthesis strategy for HRRP generation of stationary target
图6 所有方位HRRP合成时对应的合适测量数
Fig. 6 Proper numbers of measurements for HRRP generation in all azimuths
4.3 运动目标的序贯HRRP合成
最后，通过仿真结果分析所提动态策略的速度估计与HRRP合成性能。由于暗室测量目标没有平动，因此，通过仿真来得到运动目标回波。假设目标朝向雷达以某一速度前进，从频率步进测量数据中随机挑选目标RCS数据后乘以相应速度产生的相位项。
仍然以2个特殊的方位角(5°和45°)下的频率测量RCS数据为例。为了使仿真更接近实际，假设在5°和45°方位角下目标的速度分别为25 m/s和75 m/s，而且可以通过粗略估计得到2个速度分别随机处于[20，30] m/s和[70，80] m/s。速度范围被分成L=10个网格点，利用1.2小节的动态策略处理合成的数据，可以得到速度的估计值和相应的HRRP。
为了得到算法的统计性能，进行20次蒙特卡洛仿真，结果如图7所示。
图7 基于动态合成策略的运动目标速度估计与HRRP合成结果
Fig. 7 Results of moving target velocity measurement and HRRP generation using dynamic synthesis strategy
从图7(a)可见：当测量个数大于40时，目标在5°方位角下的速度估计值始终比较精确，而对于方位角为45°的情况，对应的最小测量数为26；除了速度的精确估计，相邻HRRP的ANCC也需要足够大，才能最终确定1个CPI中最优的脉冲个数。
从图7(b)可见：对于5°方位角的情况，当测量数大于49时，相邻HRRP的ANCC总是大于0.99，而对于45°方位角，对应的测量数为28，这与静止目标下的结果十分接近。
5 结论
(1) 针对实际中难以事先确定随机步进频压缩感知雷达所需脉冲数的问题，设计了一种动态压缩感知合成一维距离像策略。该策略主要包含1个快速序贯更新算法和1个停止准则。为实现快速序贯更新，将已有的实数同伦算法推广至复数情形，提出了高效的复值同伦算法。该算法避免了每次加入一个新的观测时都要求解一个新的优化问题，实现了快速递归稀疏恢复。此外，利用目标一维距离像的相关性特征给出了一种停止准则。基于仿真和实测数据的实验结果表明本文提出的动态策略可以根据雷达回波自适应地获得最优脉冲数，在非合作运动目标的成像方面具有明显优势。
(2) 由于本文所提的复值同伦算法具有一般性，可以广泛用于CS雷达的多个领域，如动目标检测[20]和二维成像[21]等。需要指出的是，本文将1个复数向量拆分为2个实数向量，但没有利用这2个实数向量之间的约束关系，损失了部分信息，导致其性能下降，因此，需要进一步研究性能更优的复数同伦算法。
参考文献：
[1] Berizzi F, Martorella M, Cacciamano A, et al. A contrast-based algorithm for synthetic range-profile motion compensation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10): 3053-3062.
[2] Axelsson S R J. Analysis of random step frequency radar and comparison with experiments[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(4): 890-904.
[3] Freedman A, Bose R, Steinberg B D. Thinned stepped frequency waveforms to furnish existing radars with imaging capability[J]. IEEE Aerospace and Electronic Systems Magazine, 1996, 11(11): 39-43.
[4] Bose R, Freedman A, Steinberg B D. Sequence CLEAN: A modified deconvolution technique for microwave images of contiguous targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 89-97.
[5] Potter L C, Ertin E, Parker J T, et al. Sparsity and compressed sensing in radar imaging[J]. Proceedings of the IEEE, 2010, 98(6): 1006-1020.
[6] Bourguignon S, Carfantan H, Idier J. A sparsity-based method for the estimation of spectral lines from irregularly sampled data[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 575-585.
[7] Tropp J A, Wright S J. Computational methods for sparse solution of linear inverse problems[J]. Proceedings of the IEEE, 2010, 98(6): 948-958.
[8] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[9] Candès E, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.
[10] ZHANG Lei, QIAO Zhijun, XING Mengdao, et al. High-resolution ISAR imaging with sparse stepped-frequency waveforms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4630-4651.
[11] ZHU Feng, ZHANG Qun, LEI Qiang, et al. Reconstruction of moving target’s HRRP using sparse frequency-stepped chirp signal[J]. IEEE Sensors Journal, 2011, 11(10): 2327-2334.
[12] LIU Zhen, WEI Xizhang, LI Xiang. Low sidelobe robust imaging in random frequency-hopping wideband radar based on compressed sensing[J]. Journal of Central South University, 2013, 20(3): 702-714.
[13] Asif M S, Romberg J. Dynamic updating for l1 minimization[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 421-434.
[14] Baraniuk R, Davenport M, DeVore R, et al. A simple proof of the restricted isometry property for random matrices[J]. Constructive Approximation, 2008, 28(3): 253-263.
[15] Candès E, Tao T. Near optimal signal recovery from random projections: Universal encoding strategies?[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.
[16] Malioutov D M, Sanghavi S R, Willsky A S. Sequential compressed sensing[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 435-444.
[17] Figueiredo M, Nowak R, Wright S. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-597.
[18] Donoho D L, Tsaig Y. Fast solution of l1-norm minimization problems when the solution may be sparse[J]. IEEE Transactions on Information Theory, 2008, 54(11): 4789-4811.
[19] Grant M, Boyd S. CVX: Matlab software for disciplined convex programming[EB/OL]. [2009-12-16]. http://stanford.edu/~boyd /cvx.
[20] QUAN Yinghui, ZHANG Lei, XING Mengdao, et al. Velocity ambiguity resolving for moving target indication by compressed sensing[J]. Electronics Letters, 2011, 47(22): 1249-1251.
[21] Alonso M T, López-Dekker P, Mallorquí J J. A novel strategy for radar imaging based on compressive sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4285-4295.
(编辑 陈灿华)
收稿日期：2013-06-03；修回日期：2013-08-10
基金项目：国家杰出青年科学基金资助项目(61025006)；湖南省杰出青年科学基金资助项目(11JJ1010)；国家自然科学基金面上项目(61271442，61171133)
通信作者：刘振(1983-)，男，江苏泰州人，讲师，从事雷达信号处理的研究；电话0731-84514427；E-mail：zhen_liu@nudt.edu.cn
