一种依概率值简化三角网格模型的新算法
刘湘云1,2,邹北骥1
(1. 湖南大学 计算机与通信学院,湖南 长沙,410082; 2. 中南大学 人事处,湖南 长沙,410083)
摘要: 利用网格模型简化技术,提出了一种基于概率值简化三角形网格模型的新算法。算法以到相关三角形平面距离最短的点为折叠后的新点,以可调加权控制函数作为折叠误差控制三角形的简化顺序,通过定义分段概率函数,采用连续折叠的方式,对处于不同误差范围内的三角形以不同概率进行连续折叠,使每次误差排序后被折叠的三角形数目由原来的1个增加为若干个,减少了排序次数,加快了简化速度。编程应用结果表明,本算法实现简单,简化速度比单次折叠简化速度提高10倍以上。
关键词: 三角形折叠;概率函数;网格模型
中图分类号:TP391 文献标识码:A 文章编号: 1672-7207(2005)01-0123-05
A new Algorithm for Simplying Triangle Mesh Model Based on Probability
LIU Xiang-yun1,2, ZOU Bei-ji1
(1. College of Computer and Communication, Hunan University, Changsha 410082,China;
2. Personnel Department, Central South University, Changsha 410083, China)
Abstract: Using mesh model simplification, a new method of triangle collapse mesh simplification algorithm based on probability was proposed. In the algorithm, the point closest to relevant triangle is the new point after the triangle is collapsed. An adjustable weighted control function is used to control the order of simplification. By means of the subdivision probability function, the algorithm continuously collapses triangles with differential errors. In this way, after reordering triangles′ errors, the one collapsed triangle is increased to several ones. Accordingly the continuous collapse algorithm decreases the times of the sort and speeds up the simplification. The program results show that the method can be worked out easily, the simplification speed can be increased by over 10times compared with separate collapse algorithms.
Key words: triangle collapse; probability function; mesh model
在计算机图形学的许多领域,常涉及复杂几何模型的交互显示。对于过于庞大的物体模型,计算机在分析、显示、存储与传输时存在很大困难;另一方面,在这类仿真应用中,对每一种物体模型的细节进行精细刻画也是不实用的。一个较好的解决办法是根据对模型逼近程度的要求对复杂模型进行简化。 国内外许多学者对模型简化进行了一系列研究[1-13],如W.J.SCHROEDER等提出了基于顶点删除的网格删减方法[1],G.TURK等提出了基于重新细分的模型简化方法[2]。在这些算法中,B.HAMANN等提出的方法是典型的三角形折叠算法[3]。类似的折叠算法还有T.S.GIENG等定义的三角形权重为三角形面积与曲率等因素乘积的折叠算法[14],V.ISLER等将边折叠与三角形折叠结合起来构造的半实时多分辨率模型[15];周昆等将三角形折叠与QEM算法相结合构造的简化模型[16]。这些算法定义三角形权值的方法各异,但简化的过程都是单次简化,即简化权值或误差最小的一个三角形后就重新进行权值或误差的排序,由此带来的问题是用于数据更新和排序的时间长,简化速度下降。针对以上算法的缺陷,在此,作者提出了一种依概率值进行连续三角形折叠的简化算法,通过引入分段概率函数,对处于不同误差范围内的三角形以不同概率进行连续折叠,使每次误差排序后被折叠的三角形数目由原来的1个增加为若干个,达到加快简化速度的目的。用分段概率函数控制简化的误差。
1 算法描述
本算法主要分为三角形折叠误差的优先级排序与简化操作(即折叠三角形),与简化有关的基本概念见参考文献[16]。
1.1 折叠误差优先级排序
为了控制简化过程,算法采用包含简化前后相关三角形转动的二面角D(T)、折叠三角形Ti的面积S(Ti)和Ti的纵横比R(Ti)三者加权平均的控制函数F(Ti)作为简化优先的主要依据,控制函数较小的三角形优先简化。
三角形Ti的纵横比为:
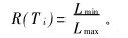
式中:Lmax和Lmin分别为Ti的最长边和最短边的长度。
三角形Ti的控制函数F(Ti)为:
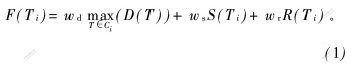
式中:wd为二面角最大值的权值;ws为S(Ti)的权值;wr为纵横比R(Ti)的权值;Ci为Ti的相关三角形集合。
控制函数中,3个分项分别从模型表面的平坦程度、面片大小和狭长程度3个方面控制简化的方向。为从整体上控制简化网格与原始网格的误差,定义一个全局误差函数C(v)为控制函数F(Ti)与三角形Ti三顶点的历史误差e(vi)之和。即当三角形Ti折叠为点v时,折叠误差C(v)为:
C(v)=F(Ti)+e(vi1)+e(vi2)+e(vi3)。(2)
设t为常数,执行该三角形折叠操作后折叠点v的历史误差e(v)为:
e(v)=tC(v)。(3)
其中:t决定了顶点v的历史误差对与v相关的三角形集合中各三角形折叠误差值的“贡献”,在本实验中取t=1,得到了较好的简化结果。
未执行任何三角形折叠操作前,即在原始网格中,各顶点历史误差均为0,即e(vi)=0。随着简化过程中三角形折叠操作的进行,因为C(v)>0,各三角形的C(v)值将不断增大,最终得到各三角形面片在整个简化过程中的全局累积误差。
所有的三角形面片都按照折叠误差从小到大排为升序优先队列进行折叠。
1.2 简化操作
1.2.1 新点位置
算法对网格进行简化的基本操作是三角形折叠。在图1(a)中,对三角形Ti=(vi1,vi2,vi3)执行折叠操作,即将它的3个顶点合并为1个顶点vi0,原来的网格简化为如图1(b)所示的形式。
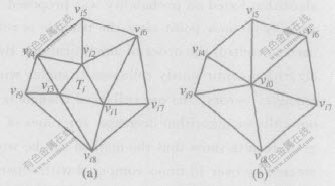
(vi1,vi2,vi3)折叠成vi0
(a)— 简化前网格; (b) — 简化后网格
图 1 三角形折叠操作
Fig. 1 Triangle collapse operation
本算法采取从三角形3个顶点、3边中点和重心共7个候选点中选择1个到相关三角形平面距离之和最小的点作为该三角形折叠后新点。
1.2.2 依概率函数连续折叠
按折叠误差大小将所有三角形面片排为升序优先队列后,定义一个根据当前误差范围变化的分段概率函数,所有三角形依各自分配的概率进行折叠,概率较大的三角形同时被折叠简化。其中分段概率函数P如图2所示,其构造过程如下。
设当前误差最小值为Cmin,误差最大值为Cmax,ΔC=Cmax-Cmin,根据用户设定的下限百分比m1和上限百分比m2(m1〈m2),定义误差下限阈值δ与上限阈值γ分别为:
δ=Cmin+m1ΔC;
γ=Cmin+m2ΔC。
构造分段折叠概率函数P为:
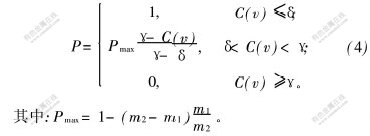
Pmax是当误差大于下限阈值时折叠概率的极大值,其变化与上下限百分比的宽度及下限百分比的变化相反,当百分比宽度和下限百分比都较大时,说明可能折叠的三角形较多,因此,用较小的概率控制实际折叠的三角形数,而当百分比宽度和下限百分比都较小时,折叠概率就相应增大。
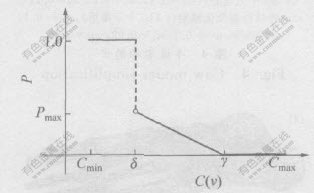
图 2 分段概率函数
Fig. 2 Subdivision probability function
上、下限阈值之间的折叠概率P是折叠误差C(v)的线形函数,即误差越小,三角形被折叠的概率越大,随着误差增大,三角形被折叠的概率逐渐减小,因此,从概率上保证了优先折叠误差较小的三角形。
从分段概率函数的构造过程可知, 用户设定的上、 下限百分比控制了概率函数值的大小和取值范围, 因此, 决定了简化模型与原始模型的误差大小。
1.3 算法流程
本算法流程如图3所示。
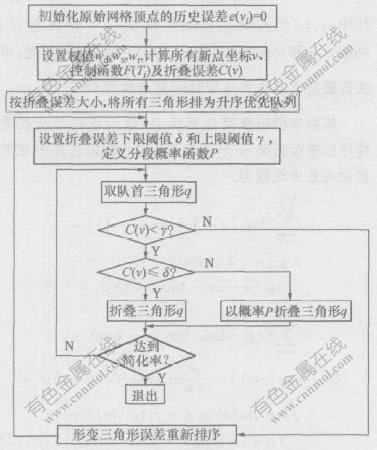
图 3 算法流程图
Fig. 3 Algorithm flow chart
2 算法分析与实验结果
三角形折叠型简化算法的实现过程是三角形折叠与误差排序的循环过程,在被折叠的三角形个数相同的前提下,减少误差排序的时间可以有效地缩短整个简化过程的时间。依概率值折叠简化算法与传统的单次折叠简化算法在简化率相同时,由于每次折叠的三角形的个数不同,排序的时间也不相同。为便于比较,假设原始模型具有n个三角形,要简化成具有n′个三角形的简化模型,采用最小值堆排序,以元素移动的最大次数作为时间复杂度的度量。
传统单次折叠简化过程中元素移动的最大次数为:
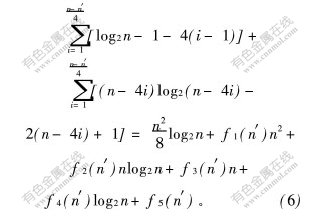
其中:f1(n′),f2(n′),f3(n′)和f4(n′)分别为n2,nlog2n,n和log2n的系数;f5(n′)为常数项。因此,单次折叠简化算法的排序时间复杂度为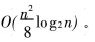
依概率值折叠简化算法中,假设平均每次误差排序后连续折叠m个三角形,整个简化过程中元素移动的最大次数为:
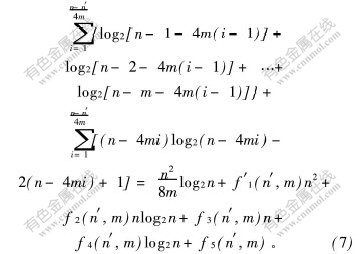
其中: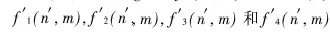
分别为n2,nlog2n,n和log2n的系数;
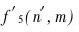为常数项。因此,依概率值连续折叠简化的时间复杂度为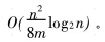
比较式(6)和式(7),虽然两者的排序复杂度的数量级相同,都为O(n2log2n),但因为该两者数量级系数相差m倍,因此,连续折叠的排序时间要比单次折叠的时间快m倍。
实验中用牛模型和脚骨模型(见图4和图5)说明本算法的性能。本算法与单次折叠算法相比较的运行时间、简化率和简化误差如表1所示。其中,简化率为简化模型的面片数与原始模型面片数的百分比,平均误差为已经折叠简化的三角形面片误差函数的平均值,时间单位为ms,运行环境为:CPU PentiumIV 2G ,RAM 256MB。实验结果表明,由于平均折叠的三角形个数增加,连续折叠简化比单次折叠简化速度要快,而2种简化方法的平均误差大致相同,得到的简化模型面片个数相近,面片大小、形状和分布相似,简化的效果一致。另外,连续折叠简化对表面较光滑和不光滑的模型数据都是有效的,如图4和图5所示,牛模型在简化70%之后与原始模型还很接近,简化结果也比较均匀;脚骨模型在简化75%后所得到的模型仍保持了原模型的基本特征。
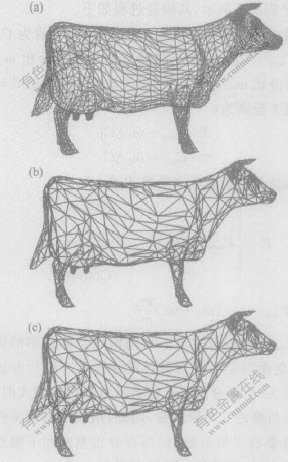
(a)—原始模型(5804个三角形); (b)—单次折叠简化模型
(1740个三角形),wd=0.1, ws=0.8, wr=0.1;
(c)—连续折叠简化模型(1740个三角形),wd= 0.1,
ws=0.8, wr= 0.1,m1=0.02, m2=0.05
图 4 牛模型的简化
Fig. 4 Cow model simplification
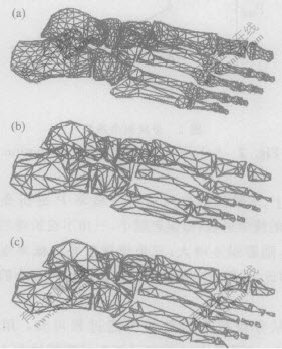
(a)—原始模型(4204个三角形); (b)—单次折叠简化模型
(1117个三角形),wd=0.3, ws=0.3, wr=0.4;
(c)—连续折叠简化模型(1048个三角形),wd= 0.3,
ws=0.3, wr= 0.4, m1=0.02, m2=0.06
图 5 脚骨模型的简化
Fig. 5 Bone model simplification
表 1 单次折叠简化与连续折叠简化运行时间对比
Table 1 Comparison of run-time between separate collapse and continuous collapse
3 结 语
a. 三角形折叠简化过程是三角形折叠与误差排序的循环过程,减少误差排序的时间可以有效地缩短整个简化过程的时间。依概率值折叠的网格简化算法通过定义分段概率函数,使误差处于不同区间的三角形以相应的概率进行连续折叠,实现了对原始模型的快速简化。
b. 依概率值进行连续折叠简化的思想可用于改进以标量误差度量简化顺序的几何元素折叠型简化算法。
c. 依概率值折叠简化的速度在同等条件下比单次折叠简化的速度快10倍以上。
参考文献:
[1]SCHROEDER W J, ZARGE J A, LORENSEN W E. Decimation of Triangle Meshes[J]. Computer Graphics, 1992,26(2):65-70.
[2]TURK G. Re-tiling Polygonal Surface[J]. Computer Graphics, 1992,26(2):55-64.
[3]HOPPE H. Progressive Meshes[J]. Computer Graphics,1996,30(1):99-108.
[4]GARLAND M, HECKBERT P S. Surface Simplification Using Quadric Error Metrics[J]. Computer Graphics,1997,31(3):209-216.
[5]HAMANN B. A Data Reduction Scheme for Triangulated Surface[J]. Computer Aided Geometric Design, l994, 11(2):197-214.
[6]ECK M, DEROSE T, DUCHAMP T, et al. Multiresolution Analysis of Arbitrary Meshes[J].Computer Graphics,1995,29(2):173-182.
[7]COHEN J,VARSHNEY A, MANOCHA D, ed al. Simplification Envelopes[J].Computer Graphics,1996,30(2): 119-128.
[8]曹卫群, 刘新国, 鲍虎军,等.基于分割插值的连续多分辨率模型[J].软件学报,2002,13(4):652-658.
CAO Wei-qun, LIU Xin-guo, BAO Hu-jun, et al. Continuous Multiresolution Modeling Based on Interpolation Subdivision[J]. Journal of Software, 2002,13(4):652-658.
[9]马小虎, 潘志庚, 石教英.基于三角形移去准则的多面体模型简化[J].计算机学报,1998,21(6):492-498.
MA Xiao-hu, PAN Zhi-geng, SHI Jiao-ying.Polyhedral Model Simplification Method Based on Triangle Removal Criterion[J].Chinese Journal of Computers, 1998,21(6):492-498.
[10]申煜湘, 邹北骥, 孙家广,等.一种基于单层包络控制的三角形网格简化算法[J].电子学报,2002,30(12A):2004-2007.
SHEN Yu-xiang, ZOU Bei-ji, SUN Jia-guang, et al. A Triangle Mesh Simplification Algorithm Based on Solo-envelope Controlled[J]. Acta Electronica Sinica, 2002,30(12A):2004-2007.
[11]吴亚东, 刘玉树, 高春晓.基于二次误差度量的网格简化算法[J].北京理工大学学报,2000,20(5):605-611.
WU Ya-dong, LIU Yu-shu, GAO Chun-xiao. Mesh Simplification Based on Quadric Error Metrics[J].Journal of Beijing Institute of Technology, 2000,20(5):605-611.
[12]汪国兴, 张明敏, 潘志庚.一种新的连续多分辨率模型自动生成算法[J].系统仿真学报,2002,14 (8):990-1003.
WANG Guo-xing, ZHANG Ming-min, PAN Zhi-geng. A New Automatic Generation Method for Multi-resolution Models[J]. Journal of System Simulation, 2002,14 (8):990-1003.
[13]蒋遂平, 周明天, 戴 颖.基于法向的网格简化[J].计算机学报,1999,22(19):1074-1079.
JIANG Sui-Ping, ZHOU Ming-tian, DAI Ying. Mesh Simplification Based on Normals[J]. Chinese Journal of Computers, 1999,22(19):1074-1079.
[14]GIENG T S,HAMAMN B,JOY K I, et al. Smooth Hierarchical Surface Triangulations[A]. Yagel R,Hagen H. Proceedings of the IEEE Visualization′97[C].San Francisco:IEEE Computer Society Press,1997:379-386.
[15] ISLER V, LAU R W H, GREEN M. Real-Time Multi-resolution Modeling for Complex Virtual Environments[A]. MARK G. Proceedings of the TRST′96[C].Hong Kong:ACM press, 1996:11-20.
[16]周昆, 潘志庚, 石教英.基于三角形折叠的网格算法[J].计算机学报,1998,21(6):506-513.
ZHOU Kun, PAN Zhi-geng, SHI Jiao-ying. Mesh Simplification Algorithm Based on Triangle Collapse[J]. Chinese Journal of Computers, 1998,21(6):506-513.
收稿日期:2004-04-20
基金项目:湖南省自然科学基金资助项目(02JJY3049)
作者简介:刘湘云(1975-),女,湖南花垣人,讲师,硕士研究生,从事计算机图形学与图像处理研究
论文联系人: 刘湘云,女,讲师,硕士研究生;电话:0731-8836270(H); E-mail: lxy612@yahoo.com.cn
