J. Cent. South Univ. Technol. (2010) 17: 845-851

DOI: 10.1007/s11771-010-0565-6

Effects of temperature change on elastic behavior of steel beams with semi-rigid connections

CAI Jian-guo(蔡建国)^{1, 2}, FENG Jian(冯健)^{1, 2}, HAN Yun-long(韩运龙)^{1, 2}

1. Key Laboratory of Concrete and Prestressed Concrete Structures, Ministry of Education,

Southeast University, Nanjing 210096, China;

2. Engineering Research Center for Prestress of Jiangsu Province, Southeast University, Nanjing 210096, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Abstract: Based on the nonlinear displacement-strain relationship, the virtual work principle method was used to establish the nonlinear equilibrium equations of steel beams with semi-rigid connections under vertical uniform loads and temperature change. Considering the non-uniform temperature distribution across the thickness of beams, the formulas for stresses and vertical displacements were presented. On the basis of a flowchart for analysis of the numerical example, the effect of temperature change on the elastic behavior of steel beams was investigated. It is found that the maximal stress is mainly influenced by axial temperature change, and the maximal vertical displacement is principally affected by temperature gradients. And the effect of temperature gradients on the maximal vertical displacement decreases with the increase of rotational stiffness of joints. Both the maximal stress and vertical displacement decrease with the increase of rotational stiffness of joints. It can be concluded that the effects of temperature changes and rotational stiffness of joints on the elastic behavior of steel beams are significant. However, the influence of rotational stiffness becomes smaller when the rotational stiffness is larger.

Key words: steel beams; semi-rigid connections; stress; displacement; stiffness; elastic behavior; temperature change; virtual work principle

1 Introduction

In recent years, long-span structures have been developed rapidly all over the world, especially in China. Many applications of these structures have been found in large industrial and public buildings like aircraft hangar, sports and exhibition halls, theaters, and railway station [1-3]. Many long-span structures are quite complex and the influence of temperature is very important in the design process since the temperature stresses and displacements due to temperature change have a great impact on the structures. Temperature stresses were discussed in details for some real projects. MA et al [4] calculated and analyzed the temperature effect on Heilongjiang TV tower through the inspection and research of structures in the frigid zones. An analytic method for the temperature stress of a double-layer hyperbolic pyramid cooling tower was introduced by ZHANG et al [5], and the effect of different boundary conditions on temperature stress was also discussed. The non-uniform environmental temperature distribution and the effect of temperature change for A380 aircraft hangar at Beijing Capital International Airport were given by PEI et al [2, 6].

Advanced structural analysis has been developed rapidly in recent years [7]. However, the Eurocode allows for the consideration of a sub-assembly approach [8]. The method is attractive because it can lead to a prescriptive representation of the structural response in theory, which may be presented in design codes. So researchers use this method to perform structural analysis under temperature load [9-11]. Most efforts in the recent studies of steel structures under non-uniform temperature change have been devoted to two main topics: (1) effects of non-uniform transverse temperature distribution across the height of steel beams, or across the thickness of columns, on their structural behavior [9-11]; and (2) effects of longitudinal non-uniform temperature distribution in continuous steel structures induced by the heat sinks at floor levels [12-14].

Semi-rigid connections, such as seat angles with web cleats, flush end plates and extended end plates details, are widely used in the construction of steel structures. It is known that assuming these connections to be either perfectly pinned or fixed joints for simplicity can cause considerable errors in structural analysis. Effects of joint flexibility on steel structures under thermal loading were discussed in Refs.[15-16].

In this work, the elastic behavior of steel beams with semi-rigid connection under vertically uniform distributed loads was investigated. The object of this study was to discuss the effect of temperature change on the structural response of steel beams. The virtual work principle method was used to establish the nonlinear equilibrium equation, and the formulas for stress and vertical displacement of beams with semi-rigid connection were obtained. Then, the effects of temperature actions and rotational stiffness of joints were studied based on a numerical example.

2 Basic theory

2.1 Nonlinear equilibrium equations

The geometry of the beam with semi-rigid connections subjected to a vertical uniform load is shown in Fig.1. In this model, the semi-rigid connections are treated as elastic rotational springs with rotational stiffness k. The axis system is selected as being centroidal, with the origin at mid-span. The temperature- dependent elastic modulus E is assumed to be constant because the temperature change is smaller than 100 ℃. Under temperature change, strain ε_t at the axial line and bending curvature ρ_t caused by an assumed linear temperature gradient, are respectively

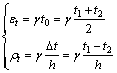                          (1)

where t₀ is the temperature increment relative to its ambient value; t₁ and t₂ are the downside and upside temperature changes of the steel beam, respectively; γ is the coefficient of thermal expansion that is taken as 1.2×10^-5/℃ in this work; and h is the depth of the beam.

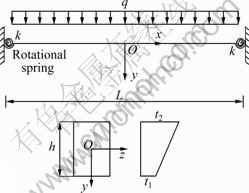
Fig.1 Geometric model of steel beams

The nonlinear strain-displacement relationship can be written as [15, 17]

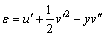                            (2)

where ( )′=d( )/dx; and u and v are the axial and vertical displacements of the beam, respectively.

On the other hand, the total strain of the beam can be described by [14]

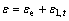                                 (3)

where ε_e is the mechanical elastic strain, and ε_{1, t} is the thermal induced strain. All the strains are defined as positive when acting in tension. And mechanical strain ε_e can be divided into two components, i.e., mechanical axial strains ε_m and mechanical bending strains ε_b. From Eqs.(1)-(3), we can obtain the mechanical axial and bending strains, shown as

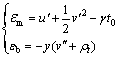                         (4)

The differential equation of equilibrium for a steel beam with semi-rigid connections under a vertical uniformly distributed load and temperature actions can be derived from the principle of virtual work that requires

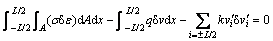  (5)

for all sets of kinematically admissible virtual strain δε and virtual displacement δv, where σ is the elastic stress of any point on the beam cross-section; A is the area of the cross-section; L is the span of the beam; and q is the vertical uniform load.

Substituting Eq.(4) into Eq.(5) produces

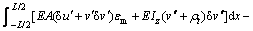
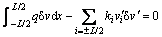             (6)

where I_z is the second moment of area, and E is the elastic modulus of steel beams.

Integrating Eq.(6) by parts, differential equilibrium equations for the axial and vertical directions can be obtained as follows:

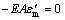                                 (7)

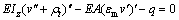                (8)

and the boundary conditions can also be produced, which are given by

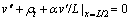                       (9)

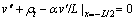                      (10)

where 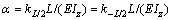 is the rotational stiffness coefficient of joints.

In addition, the other kinematic boundary condition for the beam shown in Fig.1 can be obtained as follows:

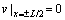                                 (11)

Eq.(11) represents that the displacements at the boundary are equal to zero.

2.2 Vertical displacements

From Eq.(7), axial strain ε_m is a constant and can be written as

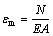                                  (12)

where N is the actual axial force in the beam, which is positive when the beam is in tension.

2.2.1 Vertical displacements under positive axial force

Substituting Eq.(12) into Eq.(8), and reducing the equation to the simplest form, the following new parameters are introduced

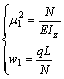                                 (13)

and then Eq.(8) can be written as

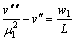                               (14)

The vertical displacement can be obtained by solving Eq.(14) with conditions Eqs.(9)-(11) as follows:

       (15)

where 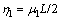is the axial force coefficient.

Then, the maximal vertical displacement, which is at the mid-span (x=0) of the steel beam, is

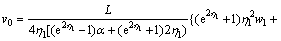
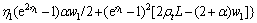 (16)

2.2.2 Vertical displacements under negative axial force

Substituting Eq.(12) into Eq.(8) and reducing the equation to the simplest form, the following new parameters are introduced

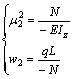                               (17)

and then Eq.(8) can be written as

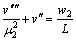                               (18)

The vertical displacement can be obtained by solving Eq.(18) with conditions Eqs.(9)-(11) as follows:

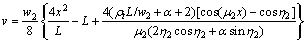(19)

where  is the axial force coefficient.

The maximal vertical displacement is at the mid- span (x=0) of the steel beams and can be written as

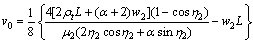    (20)

2.3 Axial forces and stress

The elastic stress of any point on the beam cross-section can be written as

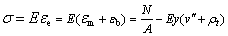        (21)

From Eqs.(15), (19) and (21), it can be seen that the only one unknown coefficient in the formulas for the displacements and stresses of steel beams is axial force coefficient η. And η can be determined by the axial equilibrium equation, in which the constant axial strain is averaged mathematically over the whole span of steel beams. This produces

                (22)

and noting that

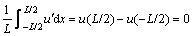             (23)

2.3.1 Stress under positive axial force

Eq.(12) can be simplified as

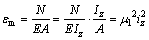                    (24)

when the beam is in tension, where i_z is the radius of gyration of the cross section about z axis given by i_z=I_z/A.

Substituting Eqs.(13) and (24) into Eq.(22) produces

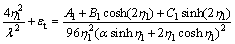       (25)

where

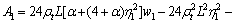
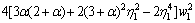
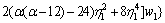
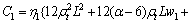
and the slenderness for the beam is λ=L/i_z.

Substituting axial force coefficient into Eq.(21), when the beam is in tension, the stress of steel beams at any point is given by

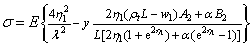    (26)

where

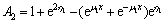
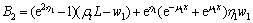
2.3.2 Stress under negative axial force

Eq.(12) can be simplified as

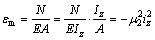                   (27)

when the beam is in compression.

Substituting Eqs.(19) and (27) into Eq.(22) produces

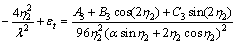        (28)

where

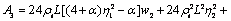
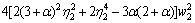
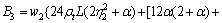
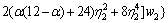
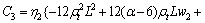
Substituting axial force coefficient into Eq.(21), when the beam is in compression, the stress of steel beams at any point can be obtained by

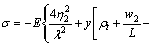
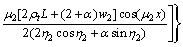             (29)

3 Numerical example and discussion

A steel beam withⅠ- section was chosen as an example for the theory described in section 2 and the effect of temperature change on the elastic behavior of steel beams with semi-rigid connection was discussed. It should be reminded that the theory presented in this work can be used for all kinds of symmetric cross-section, such as rectangle, circle, and hollow circular. The length of the beam was 8 000 mm. The cross-section of the steel beam, with an elastic modulus of 206 GPa, was 400 mm ×160 mm×12 mm×16 mm (height×width×thickness of web×thickness of flange). And the vertical uniform load on the beam was 20 kN/m.

3.1 Flowchart for analysis

It is obvious that the beam is in tension when only vertical loads are applied. Axial temperature rise creates compression in the beam, and axial temperature drop causes tensile forces in the member. Axial force coefficient η of steel beams under different temperature gradients is shown in Fig.2. It can be seen from this figure that the beam under temperature gradients is in an axial tension. The axial force is linear with the temperature gradient, and decreases with the increase of rotational stiffness of joints.

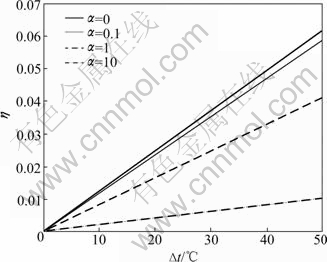
Fig.2 Effect of temperature gradient (?t) on axial force coefficient (η)

As presented in section 2, different formulas should be used for calculating the displacement and stress when the beam is in tension or in compression. Therefore, the axial force of steel beams under various vertical loads and temperature actions should be determined firstly. The flowchart, shown in Fig.3, is used for calculating the displacement and stress of steel beams.

Fig.4 shows the axial force coefficient of steel beams under different temperature actions using the flowchart shown in Fig.3. The horizontal axis of the figure is the axial temperature change at the centroid. Assuming that the temperature gradient Δt=βt₀, temperature gradient coefficient β corresponds to 0.1, 1, and 10 in Fig.4, respectively. The member is in tension initially under vertical loads and then in compression when the axial temperature changes increase. After that, it can be found that within the range of parameters considered in Fig.4, the situations equal to 0.1 and 1 result in compression throughout. But when β is 10, the member is in tension after a delineating temperature of 31 ℃ is reached. And the delineating temperature increases to 92 ℃ when the rotational stiffness coefficient of joints increases to 1. This is because the tension force produced by temperature gradient decreases with the increase of rotational stiffness of joints, as illustrated in Fig.2.

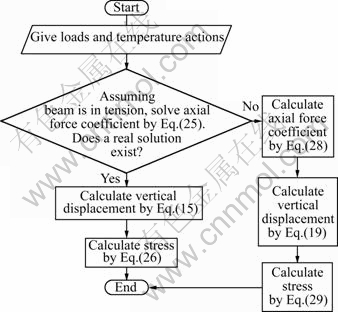
Fig.3 Flowchart for analysis of numerical example

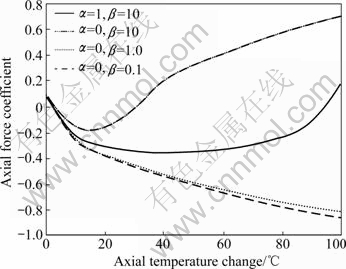
Fig.4 Axial force coefficient under different temperature actions

3.2 Effects of temperature actions

Effects of temperature actions on the elastic behavior of steel beams when the rotational stiffness of joints is equal to zero are shown in Fig.5 as the variations of the maximal stress and maximal vertical displacement with the axial temperature change at the centroid t₀ respectively. It can be seen that the maximal stress of steel beams increases whenever the axial temperature rises or drops. If the temperature gradient is not considered (β=0), the vertical displacement increases slightly with an increase of the axial temperature. But the increase of the vertical displacement becomes notable when temperature gradient coefficient β increases. And the variation of vertical displacement becomes inverse while the temperature gradient coefficient is negative. However, the maximal stress of steel beams has little correlation with temperature gradients.

Fig.5 Effects of temperature actions on elastic behavior of steel beams: (a) Maximal stress; (b) Maximal vertical displacement

3.3 Effects of rotational stiffness of joints

Fig.6 shows the effect of rotational stiffness on the elastic behavior of steel beams as the variations of maximal stress and maximal vertical displacement with rotational stiffness coefficient α when the temperature gradient is not considered. The maximal stress and vertical displacement of steel beams decrease with an increase of joint rotational stiffness. And the effect of rotational stiffness becomes smaller when the rotational stiffness is larger. The decrease of the maximal stress and vertical displacement becomes very slow when the rotational stiffness coefficient α＞4.

The relationship between the maximal vertical displacement and temperature gradient coefficient β at different rotational stiffness of beams with semi-rigid connections is illustrated in Fig.7. The vertical displacements of pin-ended beams are also given in Fig.7 for comparison. It can be found that the maximal vertical displacements of beams with semi-rigid connections are smaller than those with pin-ended beams. And the effect of temperature gradients on the maximal vertical displacement decreases with the increase of rotational stiffness of joints. When the rotational stiffness of joints is infinity (i.e., the beam is fixed), the temperature gradient will have no effect on the vertical displacement.

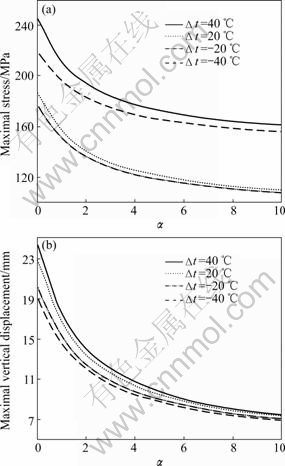
Fig.6 Effects of rotational stiffness of joints: (a) Maximal stress; (b) Maximal vertical displacement

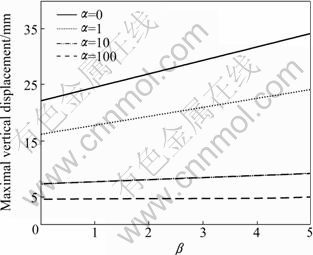
Fig.7 Effects of temperature gradient coefficient β on maximal vertical displacement at different rotational stiffness of joints

4 Conclusions

(1) The sign of axial force is controlled to a great extent by the temperature gradient coefficient β. And the influence decreases with an increase of the rotational stiffness of joints.

(2) The effects of temperature change on the elastic behavior of steel beams under vertical uniform loads are significant. The maximal stress increases with the increase of axial temperature changes. The vertical displacement has small correlation with axial temperature changes, which is influenced by the temperature gradients. However, the effect of temperature gradients on the maximal vertical displacement decreases with the increase of rotational stiffness of joints.

(3) The influence of rotational stiffness of joints on the maximal stress and vertical displacement is distinct. The maximal stress and vertical displacement reduce when the rotational stiffness of joints increases.

Acknowledgment

The first author would like to thank the China Scholarship Council to support his study in California Institute of Technology and the help of Professor PELLEGRINO S and Mr. DENG Xiao-wei.

References

[1] Chen Zhi-hua, LI Yang. Parameter analysis on stability of a suspendome [J]. International Journal of Space Structure, 2005, 20(2): 115-124.

[2] PEI Yong-zhong, BAI Yin, SHI Yong-jiu, ZHU Dan, WANG Yuan-qing. Temperature distribution in a long-span aircraft hangar [J]. Tsinghua Science and Technology, 2008, 13(2): 184-190.

[3] Cai Jian-guo, Feng Jian, Chen Yao, HUANG Li-feng. Study on the seismic performance of space beam string structures [C]// Proceeding of the 14th World Conference on Earthquake Engineering. Beijing: 2008: 05-01-0131.

[4] Ma Ren-le, Sun De-fa, Yao Mei-ming. The influence of temperature effect on Heilongjiang TV tower [J]. Shanghai Journal of Mechanics, 1999(4): 404-409. (in Chinese)

[5] Zhang Hui, Ying Zhi-xiang, Li Jing-sheng. The research on temperature stress of cooler tower of double hyperbolic reticulated shell [J]. Steel Construction, 2003(4): 37-39. (in Chinese)

[6] Zhu Dan, Pei Yong-zhong, Xu Rui, TANG Hong-jun, ZENG Di, ZHAO Tian-you. Design and research on the long-span structure of Beijing A380 hangar [J]. Chinese Journal of Civil Engineering, 2008, 41(2): 1-8. (in Chinese)

[7] Liew J Y R, Ma K Y. Advanced analysis of 3D steel framework exposed to compartment fire [J]. Fire and Materials, 2004, 28(2/4): 253-267.

[8] TRAHAIR N S, CHAN S L. Out-of-plane advanced analysis of steel structures [J]. Engineering structures, 2003, 25(13): 1626-1637.

[9] Yin Y Z, Wang Y C. Numerical simulations of the effects of nonuniform temperature distributions on lateral torsional buckling resistance of steel I-beams [J]. Journal of Constructional Steel Research, 2003, 59: 1009-1033.

[10] Li Shi-rong, Song Xi. Large thermal deflections of Timoshenko beams under transversely non-uniform temperature rise [J]. Mechanics Research Communications, 2006, 33: 84-92.

[11] Wong M B. Adaptation factor for moment capacity calculation of steel beams subject to temperature gradient [J]. Journal of Constructional Steel Research, 2007, 63: 1009-1015.

[12] Becker R. Structural behavior of simple steel structures with non-uniform longitudinal temperature distributions under fire conditions [J]. Fire Safety Journal, 2002, 37: 495-515.

[13] Chen Chang-kun, Yao Bin, Xu Zhi-sheng, FAN Wei-cheng. Effects of longitudinally non-uniform temperature distribution on steel beams under fire conditions [J]. Journal of University of Science and Technology of China, 2006, 36(1): 103-109.

[14] Tan K H, Yuan W F. Buckling of elastically restrained steel columns under longitudinal non-uniform temperature distribution [J]. Journal of Constructional Steel Research, 2008, 64: 51-61.

[15] Bradford M A. Elastic analysis of straight members at elevated temperatures [J]. Advances in Structural Engineering, 2006, 9(5): 611-618.

[16] Al-Jabri K S, Davison J B, Burgess I W. Performance of beam-to-column joints in fire: A review [J]. Fire Safety Journal, 2008, 43: 50-62.

[17] Cai Jian-guo, Feng Jian, Chen Yao, HUANG Li-feng. In-plane stability of fixed parabolic shallow arches [J]. Science in China Series E: Technological Sciences, 2009, 52(3): 596-602.

Foundation item: Project(50478075) supported by the National Natural Science Foundation of China; Project(YBJJ0817) supported by Scientific Research Foundation of Graduate School of Southeast University

Received date: 2009-09-29; Accepted date: 2010-03-11

Corresponding author: FENG Jian, PhD, Professor; Tel: +86-25-83793150; E-mail: caijg_ren@126.com

(Edited by CHEN Wei-ping)