Trans. Nonferrous Met. Soc. China 22(2012) s668-s672

Determination of critical parameters for dynamic recrystallization in Ti-6Al-2Zr-1Mo-1V alloy

XIA Yu-feng, LIU Ying-ying, MAO Yuan-ping, QUAN Guo-zheng, ZHOU Jie

College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China

Received 21 May 2012; accepted 18 October 2012

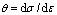Abstract: The true stress—strain curves of Ti-6Al-2Zr-1Mo-1V alloy were achieved by a series of isothermal compression tests with height reduction of 60% under the deformation temperatures of 1073-1323 K and the strain rates of 0.01-10 s^-1. The critical conditions for the onset of DRX were attained when the value of , where strain hardening rate , reached the minimum which corresponds to an inflection of θ versus σ curve. Thus, two important potential parameters, critical strain and critical stress, were identified, and expressed as ε_c/ε_p=0.37-0.60, σ_c/σ_p=0.81-0.91. Furthermore, by the regression analysis for conventional hyperbolic sine equation, the main material parameters such as α, β, n, and DRX activation energy, Q, were calculated. In addition, the evolution of Q with strain rate and temperature was revealed as a 3D response surface.

Key words: Ti-6Al-2Zr-1Mo-1V alloy; dynamic recrystallization; flow stress; strain hardening rate; activation energy

1 Introduction

Ti-6Al-2Zr-1Mo-1V alloy has been extensively used for aerospace applications because of its attractive combination of properties such as high specific strength, excellent fracture toughness and good heat/corrosion resistance. To make large structural components cost effective and to meet the required mechanical properties, production is usually fabricated via hot near net shape forging [1]. However, the microstructure and resulting properties of most near-α alloys are very sensitive to forming variables, even during isothermal forming. To date, successful forging has relied on significant empirical optimization. During hot forming process, titanium alloy is liable to undergo work hardening (WH), dynamic recovery (DRV) and dynamic recrystallization (DRX), which are three metallurgical phenomena controlling the microstructure and mechanical properties [2,3]. Due to the low stacking fault energy of (α+β)/β phase in the Ti-6Al-2Zr-1Mo-1V alloy, the major restoration process during hot deformation is dynamic recrystallization (DRX) [4]. Initiation of DRX is truly dynamic and not predetermined by a simple deformation parameter like the critical strain. At a given temperature, DRX occurs at a critical stress for a constant strain rate (dynamic test) or at a critical strain rate for a constant stress (creep test). However, the critical stress or strain rate, respectively, depends on deformation conditions and material characteristics [5].

The true stress—strain curve expresses the state of microstructure at given deformation condition, thus, by which the prediction of DRX onset critical conditions can be performed. In the present work, the flow stress curve for as-cast Ti-6Al-2Zr-1Mo-1V alloy has two characteristic parameters including the critical strain for DRX initiation (ε_c) and the critical stress for DRX initiation (σ_c). This means that the initiation of DRX can be expressed by the process variables. The objective of this work is to identify ε_c, σ_c, and the DRX activation energy, Q.

2 Experimental

The as-cast Ti-6Al-2Zr-1Mo-1V alloy employed in the present work was provided in the form of bar with the diameter of 300 mm. The chemical compositions of Ti-6Al-2Zr-1Mo-1V used in this work are (mass fraction, %) Al 6.60, V 2.31, Mo 1.70, Zr 2.20, Fe 0.06, Ti balance. Before the experiment, the compression specimens, with the diameter of 10 mm and the length of 12 mm, were machined with their cylinder axes parallel to the axial line direction of the bar. On a computer- controlled servo-hydraulic Gleeble 1500 machine, the specimens were heated at a rate of 1 K/s and held at a certain temperature for 180 s to ensure a uniform starting temperature and decrease the material anisotropy. All the 16 specimens were compressed to true strain of 0.9163 (height reduction 60%) at the temperatures of 1073, 1123, 1173, 1223, 1273 and 1323 K, and the strain rates of 0.01, 0.1, 1 and 10 s^-1, then immediately water cooled down to retain the recrystallized microstructures. During the compressing process, the variations of stress and strain were monitored continuously by a personal computer equipped with an automatic data acquisition system. The true stress—strain relationships were derived from the nominal stress—strain curves collected according to the following formula: , , 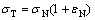where σ_T is the true stress, σ_N is the nominal strain, ε_T is the true strain and ε_N is the nominal strain [6,7].

3 Results and discussion

3.1 Plastic flow behavior at elevated temperatures

The true compressive stress—strain curves for as-cast Ti-6Al-2Zr-1Mo-1V alloy under different temperatures and strain rates are illustrated in Fig. 1. The flow stress as well as the shape of the flow curves is sensitively dependent on temperature and strain rate. It is found that the stress level decreases with the increase of temperature and decrease of strain rate because lower strain rate provides longer time for the energy accumulation and higher temperature provides higher mobilities at boundaries which result in the nucleation and growth of dynamically recrystallized grains and dislocation annihilation [8-10]. From all the curves, two types of curve variation tendency can be generalized: decreasing continuously with significant DRX softening (1073 K and 0.01 s^-1, 1123 K and 0.01 s^-1, 1073 K and 0.1 s^-1, 1123 K and 0.1 s^-1, 1073 K and 1 s^-1, 1123 K and 1 s^-1, 1173 K and 1 s^-1, 1073 K and 10 s^-1, 1123 K and 10 s^-1, 1173 K and 10 s^-1), keeping steady-state without any peak due to dynamic recovery (DRV) (1173 K and 0.01 s^-1, 1223 K and 0.01 s^-1, 1273 K and 0.01 s^-1, 1323 K and 0.01 s^-1, 1173 K and 0.1 s^-1, 1223 K and 0.1 s^-1, 1273 K and 0.1 s^-1, 1323 K and 0.1 s^-1, 1223 K and 1 s^-1, 1273 K and 1 s^-1, 1323 K and 1 s^-1, 1223 K and 10 s^-1, 1273 K and 10 s^-1, 1323 K and 10 s^-1). Thus, it can be concluded that the typical form of flow curve with DRX softening, including a single peak followed by continuously decreasing, is more recognizable at lower temperatures and higher strain rates, while another typical form of flow curve with DRV softening, without any peak, is more recognizable at higher temperatures and lower strain rates.

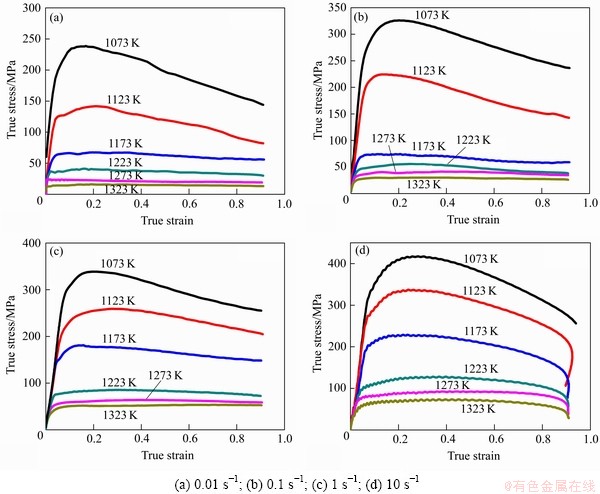
Fig. 1 True stress—strain curves of as-cast Ti-6Al-2Zr-1Mo-1V alloy obtained by Gleeble 1500 under different deformation temperatures and different strain rates

3.2 Observation of DRX

Figure 2(a) show the initial equiaxed α + β microstructure of as-cast Ti-6Al-2Zr-1Mo-1V alloy. Figures 2(b)-(d) show the grains of specimens compressed with height reduction of 60% under 1073, 1173 and 1273 K at a strain rate of 0.01 s^-1. Ti-6Al-2Zr-1Mo-1V is a two-phase titanium alloy with a β transus (α + β→β) in the temperature range of 1243-1263 K depending on the interstitial impurity (primarily oxygen) content. Figures 2(b)-(c) show that under 1073 K and 1173 K, the microstructure of the deformed specimens is characterized quantitatively in terms of α and β phase size and morphology, and the amount of intergranular β phase increases as temperature rises from 1073 K to 1173 K. Figure 2(d) shows that as temperature rises to 1273 K across the phase trans- formation temperature 1243-1263 K, α phase transforms to β phase completely, and the microstructure is entirely composed of β phase. From Figs. 2(b) and (c), it can be seen that the grains in α phase partially transforms to a microstructure of approximately equiaxed defect- free grains which are predominantly bounded by high angle boundaries (i.e. a recrystallized microstructure) by relatively localized boundary migration. Meanwhile, the grains in β phase transformed from α phase are also suffering DRX microstructural evolution. From Fig. 2(d), it can be seen that very small acicular crystals have been formed all over the complete β phase.

3.3 Identification for critical parameters of DRX

The critical conditions for the onset of DRX are attained when the value of , where strain hardening rate 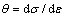, reaches the minimum which corresponds to an inflection of dσ/dε vs σ curve [11,12]. In this work, analysis of inflections in the plot of dσ/dε vs σ up to the peak point of the true stress—strain curve has been performed to reveal whether DRX occurs. Results confirm that there appear the inflections in the dσ/dε vs σ curves as shown in Figs. 3(a)-(d), which clearly indicate that DRX occurs in the above deformation conditions. Therefore, this method was used to determine the values of critical strain and critical stress at different deformation conditions, then the relationships between critical strain ε_c and peak strain ε_p, and between critical stress σ_c and peak stress σ_p are given in Table 1. From Table 1, it can be seen that the critical strain and critical stress depend on temperature and strain rate nonlinearly, and it is summarized that, ε_c/ε_p= 0.37-0.60, σ_c/σ_p=0.81-0.91.

Fig. 2 Microstructures of alloys deformed at strain rate of 0.01 s^-1 and different temperatures

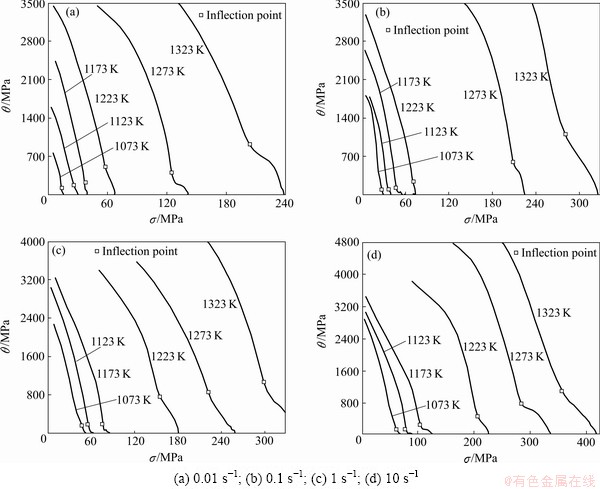
Fig. 3 dσ/dε vs σ plots up to peak points of true stress—strain curves under different deformation temperatures at different strain rates

3.4 Identification for DRX activation energy

It is known that the thermally activated stored energy developed during deformation controls softening mechanisms which induce different DRX softening and work-hardening. The activation energy of DRX, an important material parameter, determines the critical conditions for DRX initiation. So far, several empirical equations have been proposed to determine the deformation activation energy and hot deformation behavior of metals. The most frequently used one is Arrhenius equation which designs a famous Zener-Hollomon parameter, Z, to represent the effects of the temperatures and strain rate on the deformation behaviors, and then uncovers the approximative hyperbolic law between Z parameter and flow stress [6].

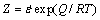                            (1)

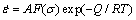                       (2)

where

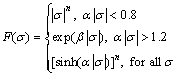
where 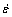 is the strain rate (s^-1), R is the universal gas constant (8.31 J/(mol·K)), T is the absolute temperature (K), Q is the activation energy of DRX (kJ/mol), σ is the flow stress (MPa) for a given strain, A, α and n are the material constants (α=β/n).

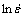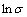In order to calculate such material constants, the stresses at true strain of 0.25, 0.45, 0.65 and 0.85 have been selected as the representative stress array of each curve. The stress exponent n is obtained from the  vs  plots, and the mean value of all the slope rates is accepted as n, 5.392. Constant nα is obtained from the σ vs  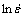plots, and the mean value of all the slope rates is accepted as nα, 0.03843 MPa^-1, thus α=0.007127 MPa^-1. The activation energy of DRX is a term defined as the energy that must be overcome for the nucleation and growth of new surface or grain boundary to occur. It is well known that the slopes of the linear curves between  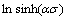and 1/T are accepted as the values of Q/(Rn). In order to reveal the influence of strain rate and temperature on Q, a quadratic polynomial curve is fitted between  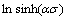and 1/T, thus the value of dynamic tangent vector on this curve is accepted as the dynamic value of Q/(Rn) corresponding to different strain rates and temperatures. Through the method illustrated above, the Q values at different strain rates and temperatures are obtained and shown in Fig. 4.

Table 1 Values of critical strain, critical stress under different deformation conditions identified from hardening rate curves

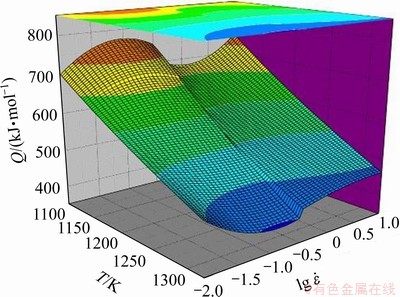
Fig. 4 3D response surface of Q vs temperature and strain rate

4 Conclusions

1) The typical form of flow curve with DRX softening, including a single peak followed by continuously decreasing, is more recognizable at lower temperatures and higher strain rates, while another typical form of flow curve with DRV softening, without any peak, is more recognizable at higher temperatures and lower strain rates.

2) Based on the true stress—strain curves, two characteristic parameters including the critical strain for DRX initiation (ε_c) and the critical stress for DRX initiation (σ_c) have been identified, and expressed as ε_c/ε_p=0.37-0.60, σ_c/σ_p=0.81-0.91.

3) In consideration of the influence of strain rate and temperature on the thermal activation of DRX, the Arrhenius type equation involving main deformation conditions is introduced, and then the main material parameters such as α, β, n, and DRX activation energy, Q, are calculated.

References

[1] ZHAO Y, GUO H Z, SHI Z F, YAO Z K, ZHANG Y Q. Microstructure evolution of TA15 titanium alloy subjected to equal channel angular pressing and subsequent annealing at various temperatures [J]. Journal of Materials Processing Technology, 2011, 211(8): 1364-1371.

[2] LINA Y C, CHENA M S, ZHANG J. Modeling of flow stress of 42CrMo steel under hot compression [J]. Materials Science and Engineering A, 2009, 499(1-2): 88-92.

[3] LIN Y C, CHEN M S, ZHONG J. Numerical simulation for stress/strain distribution and microstructural evolution in 42CrMo steel during hot upsetting process [J]. Computational Materials Science, 2008, 43(4): 1117-1122.

[4] MANDAL S, SIVAPRASAD P V, SARMA V S. Dynamic recrystallization in a Ti modified austenitic stainless steel during high strain rate deformation [J]. Materials and Manufacturing Processes, 2010, 25(1-3): 54-59.

[5] GOTTSTEING,FROMMERT M, GOERDELER M, N. Prediction of the critical conditions for dynamic recrystallization in the austenitic steel 800H [J]. Materials Science and Engineering A, 2004, 387-389(15): 604-608.

[6] QUAN G Z, SHI Y, WANG Y X, KANG B S, KU T W, SONG W J. Constitutive modeling for the dynamic recrystallization evolution of AZ80 magnesium alloy based on stress—strain data [J]. Materials Science and Engineering A, 2011, 528(28): 8051-8059.

[7] QUAN G Z, KU T W, SONG W J, KANG B S. The workability evaluation of wrought AZ80 magnesium alloy in hot compression [J]. Materials & Design, 2011, 32(4): 2462-2468.

[8] McQUEEN H J, JONAS J J. Recovery and recrystallization in the hot-working of aluminum alloys [J]. Treatise on Materials Science and Technology, 1975, 6: 393-399.

[9] ZHENG Q G, YING T, JIE Z. Dynamic softening behavior of AZ80 magnesium alloy during upsetting at different temperatures and strain rates [J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2010, 24(11): 1707-1716.

[10] LI H Z, LI Z, ZHANG W, WANG Y, LIU Y, WANG H J. High temperature deformability and microstructural evolution of Ti-47Al-2Cr-0.2Mo alloy [J]. Journal of Alloys and Compounds, 2010, 508(2): 359-363.

[11] RYAN N D, McQUEEN H J. Flow stress, dynamic restoration, strain hardening and ductility in hot working of 316 steel [J]. Journal of Materials Processing Technology, 1990, 21(2): 177-199.

[12] MANONUKUL A, DUNNE F P E. Initiation of dynamic recrystallization under inhomogeneous stress states in pure copper [J]. Acta Materialia, 1999, 47(17): 4339-4354.

(Edited by HE Yun-bin)

Foundation item: Project (2012ZX04010081) supported by the National Key Technologies R&D Program of China; Project (cstc2009aa3012-1) supported by the Science and Technology Committee of Chongqing, China; Project (CDJZR12130045) supported by the Fundamental Research Funds for the Central Universities, China

Corresponding author: XIA Yu-feng; Tel: +86-23-65103065, +86-13452877856; E-mail: quangz_2006@yahoo.com.cn

DOI: 10.1016/S1003-6326(12)61783-X