直逆向过岔列车与桥上道岔耦合振动影响因素分析

曾志平¹，陈秀方¹，余志武¹，赵国藩²

(1. 中南大学 土木建筑学院，湖南 长沙，410075；

2. 大连理工大学 土木水利学院，辽宁 大连，116024)

摘  要：针对桥上无缝道岔，运用有限单元法，建立钢轨-岔枕-桥梁弹簧-阻尼空间振动模型；运用弹性系统动力学总势能不变值原理及形成矩阵的“对号入座”法则建立列车-道岔-桥梁空间振动方程组；以温福客运专线田螺大桥为例，拟定桥上铺设了由2组38号道岔组成的单渡线，分析直逆向过岔时，列车运行速度、轨下垂向刚度、枕下垂向均布刚度、岔区垂向不平顺幅值及梁体高度等参数对列车-道岔-桥梁系统耦合振动的影响。研究结果表明：系统响应随列车速度和岔区垂向不平顺幅值增大、梁体高度减小而增加；轨下垂向刚度对系统不同的响应有不同的影响；道岔响应随枕下垂向均布刚度增大而降低。

关键词：桥上无缝道岔；列车；直向过岔；振动

中图分类号：U211.3         文献标识码：A         文章编号：1672-7207(2008)04-0856-06

Analysis of influence of some factors on train-turnout on bridge coupling vibration with train running in main direction

ZENG Zhi-ping¹, CHEN Xiu-fang¹, YU Zhi-wu¹, ZHAO Guo-fan²

(1. School of Civil and Architectural Engineering, Central South University, Changsha 410075, China;

(2. School of Civil and Hydraulic Engineering, Dalian University of Technology, Dalian 116024, China)

Abstract: Aimed at seamless turnout on bridge, the rail-turnout tie-bridge spring-damping vibration model was built by using finite element method. The train-turnout-bridge spatial vibration equation sets were formulated by using the principle of total potential energy with stationary value in elastic system dynamics and the “set-in-right-position” rule for formulating matrixes. Taking Tian-luo major bridge in Wenzhou—Fuzhou railway line for passenger as an example, it was assured that there was a crossover combined with two No.38 turnouts on the bridge. The influences of some factors on the train-turnout-bridge system coupling vibration with train running in the main direction were analyzed, such as train velocity, the vertical stiffness under rail, the vertical uniform stiffness under tie, the amplitude of vertical irregularity in turnout area, the height of beam and so on. The results show that the system responses increase with the increase of train velocity, the increase of the amplitude of vertical irregularity in turnout and the decrease of the height of beam. The vertical stiffness under rail has different influences on different responses of the system. Turnout responses decrease with the increase of the vertical uniform stiffness under tie.

Key words: seamless turnout on bridge; train; through turnout in main direction; vibration

我国客运专线建设已经全面展开，京沪(北京—上海)、武广(武汉—广州)、温福(温州—福州)、合武(合肥—武汉)等客运专线项目均有多组无缝道岔铺设在桥上，桥上无缝道岔技术综合了桥上无缝线路、无缝道岔以及大跨度桥梁的技术特点，衍生出一系列新的技术特点，是铁路轨道工程研究领域的一个全新课题。

目前，国内尚无桥上无缝道岔的实践经验，对桥上无缝道岔的理论研究刚刚起步，尚未形成系统的桥上无缝道岔计算理论和设计方法。桥上无缝道岔问题已成为制约客运专线轨道设计、施工的技术瓶颈。开展客运专线桥上无缝道岔纵向力和列车-道岔-桥梁系统振动研究，对于我国客运专线建设具有重大意义。一些研究者^[1-4]研究了温度荷载作用下，桥上无缝道岔受力与变形的规律，但对列车-道岔-桥梁系统振动的研究很少。

1  车辆空间振动模型及振动方程组

1.1  车辆空间振动模型

车辆采用整车模型^[5-7]，假设轮对与钢轨垂向密贴，车体和前后构架各具有5个自由度，分别为沉浮、横摆、侧滚、点头和摇头，每个轮对具有横摆和摇头自由度，即每辆四轴车有23个自由度。

1.2  车辆空间振动方程组的建立

车辆空间振动总势能包括车体、构架和轮对的惯性力势能和重力势能、轮对重力刚度引起的势能以及车辆悬挂系统的弹性应变能和阻尼力势能。据弹性系统动力学总势能不变值原理^[5]，对车辆总势能的表达式进行一阶变分，并运用形成矩阵的“对号入座”法则^[8-10]即可得到车辆空间振动方程组。

2  桥上道岔空间振动模型及振动方程组

2.1  桥上道岔空间振动模型

选择如图1~4所示桥上可动心轨道岔空间振动分析模型，基本假定如下：

a. 钢轨和桥梁视为等截面Euler梁，对于钢轨和梁体变截面处，近似简化为分段等截面；钢轨考虑垂向和横向变形，桥梁考虑垂向、横向和扭转变形。

b. 钢轨与岔枕之间、岔枕与道床之间的连接用线性弹簧和阻尼器模拟。将道床质量计入桥梁质量之中，假设其振动响应与桥梁的一致。

c. 岔枕在垂向视为变截面弹性点支承有限长Euler梁，其参振质量和抗弯刚度由岔枕、滑床台、铁垫板的抗弯刚度共同决定，支点垂向刚度、支点垂向阻尼分别由道床垂向均布刚度、垂向均布阻尼和岔枕单元长度共同确定。不考虑岔枕的轴向、剪切和扭转变形。忽略轨枕端部道床的横向弹性和阻尼，假设道床所提供的弹性和阻尼与岔枕长度成正比。

d. 尖轨与基本轨、尖轨与滑床台以及可动心轨与翼轨的贴靠作用均视为点接触，并以单向弹簧模拟其接触刚度。

e. 轮对与护轨的横向冲击、顶铁对钢轨横向位移的限制作用均以单向弹簧模拟，尖轨和心轨锁闭装置对钢轨位移的限制作用以双向弹簧模拟，不计顶铁和锁闭装置的质量；间隔铁对钢轨横向和垂向位移的限制作用以双向弹簧模拟，其参振质量计入相应的钢轨节点中。

图1  道岔-桥梁振动平面示意图

Fig.1  Plane sketch of turnout and bridge vibration

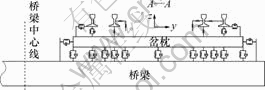
图2  尖轨截面处钢轨-岔枕-桥梁振动模型

Fig.2  Rail-turnout tie-bridge vibration model in section of switch rail

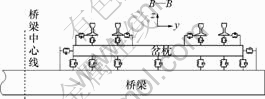
图3  导轨截面处钢轨-岔枕-桥梁振动模型

Fig.3  Rail-turnout tie-bridge vibration model in section of guide rail

图4  心轨截面处钢轨-岔枕-桥梁振动模型

Fig.4  Rail-turnout tie-bridge vibration model in section of point rail

2.2  桥上道岔空间振动方程组的建立

将钢轨和桥梁以轨枕间距为单元长度划分单元，并以轨枕支点为单元节点；岔枕以钢轨支点、铁垫板端点、岔枕端点及中点为节点划分单元，保证每个单元为等截面单元。由于道岔不同部位的结构不同，道岔-桥梁模型中存在多种钢轨-岔枕-桥梁单元。运用弹性系统动力学总势能不变值原理和形成矩阵的“对号入座”法则分别组集桥上道岔各单元的刚度矩阵、阻尼矩阵、质量矩阵以及节点荷载列阵，可得桥上道岔的空间振动方程组。详细推导过程参见文献[11]。

2.3  道岔区不平顺激励模型

转辙区和辙叉区垂向不平顺采用规范化的不平顺函数^[12-13]：

2.4  轮轨力分配

当车轮从1根钢轨过渡到另外1根钢轨时，存在轮轨垂向力的分配问题。本文根据已有的研究成果^[13]和实测结果^[15]，也采用通过拟定轮载分配系数的办法，来处理道岔共同承载区内2根轨线上轮轨垂向力的分配问题。

3  列车-道岔-桥梁空间振动方程组的建立及求解

机车车辆依次进入线路单元，在线路上的位置随时间变化。可先建立t时刻各节车辆的质量矩阵[M_vi]、阻尼矩阵[C_vi]、刚度矩阵[K_vi]和荷载列阵{P_vi}，然后视各节车辆在轨道上的位置，分别与桥上道岔的质量矩阵[M_t]、阻尼矩阵[C_t]、刚度矩阵[K_t]和荷载列阵{P_t}拼装，得出t时刻列车-道岔-桥梁的质量矩阵[M]、阻尼矩阵[C]、刚度矩阵[K]和荷载列阵{P}，从而建立t时刻的列车-道岔-桥梁空间振动方程组：

采用Wilson-θ法可对式(1)进行求解。

4  直逆向过岔时列车-道岔-桥梁振动影响因素分析

以一组单渡线铺设于1座混凝土连续刚构桥上为例，分析直逆向过岔时，列车速度、轨下垂向刚度、枕下垂向均布刚度、岔区垂向不平顺幅值、梁体高度对列车-道岔-桥梁系统振动的影响。桥梁选取温福客运专线田螺大桥，桥跨组成：32 m简支+(88+160+88) m刚构，线间距为4.6 m。拟定单渡线由2组秦沈客运专线38号无缝道岔组成，全长272.4 m，居中布置于连续刚构梁上(见图5)。计算列车为“中华之星”电动车组，编组方式为“一动四拖”。轨道随机不平顺采用秦沈客运专线实测轨道不平顺样本。

图5  渡线-田螺大桥平面示意图

Fig.5  Plane sketch of crossover and Tian-Luo major bridge

4.1  列车速度的影响

列车从1号岔位直逆向通过时，速度对列车-道岔-桥梁系统振动的影响如表1、表2及图6~8所示。结果表明，系统的各种动力响应均随列车速度的增大而增加；当列车速度为260 km/h时，动车的轮轴横向力和垂向Sperling指标分别为61.55 kN和2.926，拖车轮轴横向力和脱轨系数为43.87 kN和0.792，均接近允许值。

表1  参数对道岔和桥梁振动的影响

Table 1  Influences of parameters on turnout and bridge vibration

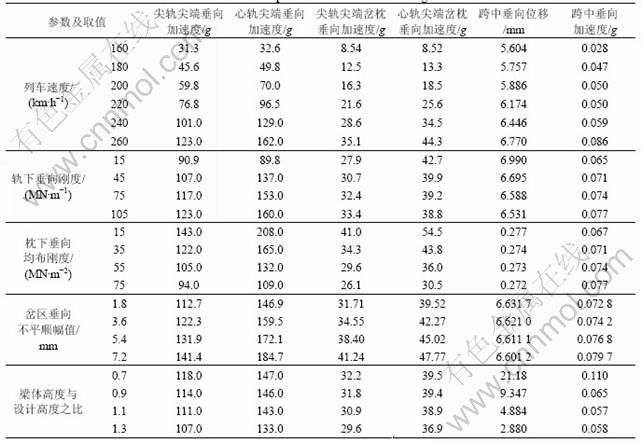
表2  参数对列车振动的影响

Table 2  Influences on parameters to train vibration

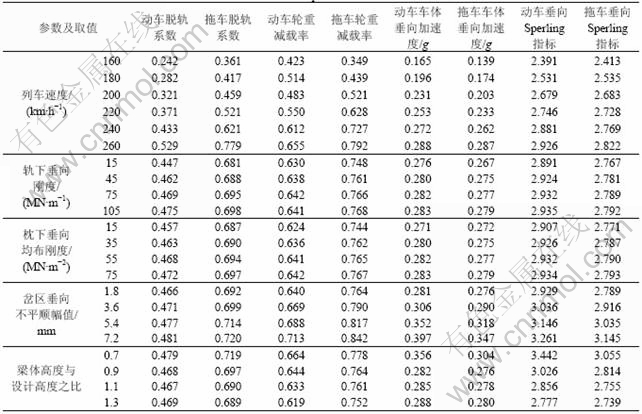
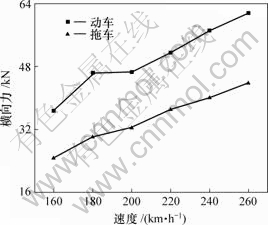
图6  轮轴横向力最大值与速度的关系曲线

Fig.6  Relationship between maximal wheel axle lateral force and velocity

图7  车体垂向Sperling指标最大值与速度的关系曲线

Fig.7  Relationship between carbody maximal vertical Sperling index and velocity

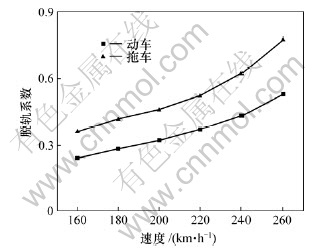
图8  脱轨系数最大值与速度的关系曲线

Fig.8  Relationship between maximal derailment coefficient and velocity

4.2  轨下垂向刚度的影响

列车以250 km/h从1号岔位直逆向通过时，轨下垂向刚度对列车-道岔-桥梁系统振动的影响如表1和表2所示。结果表明，轨下垂向刚度主要影响系统的垂向振动，对其横向振动影响很小。轨下垂向刚度由15 MN/m增加至105 MN/m，尖轨尖端、心轨尖端垂向振动加速度增幅较大，分别由90.9g(1g=9.8 m/s²)，89.8g增加至123.0g和160.0g；心轨尖端岔枕垂向振动加速度由42.7g降低至38.8g；脱轨系数、轮重减载率、垂向Sperling指标有所增大。总体而言，轨下垂向刚度对系统不同的响应有不同的影响，应控制在合理范围内。

4.3  枕下垂向均布刚度的影响

列车以250 km/h从1号岔位直逆向通过时，枕下垂向均布刚度对列车-道岔-桥梁系统振动的影响如表1和表2所示。结果表明，枕下垂向均布刚度主要影响系统的垂向振动，对其横向振动影响很小。枕下垂向均布刚度由15 MN/m²增加至75 MN/m²，尖轨尖端、心轨尖端、尖轨尖端岔枕、心轨尖端岔枕垂向振动加速度降幅较大，分别由143.0g，208.0g，41.0g和54.5g降至94.0g，109.0g，26.1g和30.5g；跨中垂向位移有所减小；脱轨系数、轮重减载率、车体垂向Sperling指标变化不明显。总体而言，增大枕下垂向均布刚度有利于降低道岔的动力响应。

4.4  岔区垂向不平顺幅值的影响

列车以250 km/h从1号岔位直逆向通过时，岔区垂向不平顺幅值对列车-道岔-桥梁系统振动的影响如表1和表2所示。结果表明，列车-道岔-桥梁系统的横向和垂向动力响应均随岔区垂向不平顺幅值的增大而有不同程度的增加，钢轨振动加速度、轮轨垂向力、轮重减载率、车体垂向振动加速度、车体垂向Sperling指标的增幅尤为明显。当岔区垂向不平顺幅值为5.4 mm时，拖车轮重减载率为0.817，动车和拖车的垂向Sperling指标分别为3.146和3.035，均超过允许值；动车垂向加速度为0.352g，接近安全管理目标值。控制岔区垂向不平顺在运营过程中发展，对于降低系统的动力响应，提高列车运行的舒适性，保障列车运行的安全性具有十分重要的意义，岔区垂向不平顺幅值应控制在3.6 mm以内。

4.5  梁体高度的影响

将梁体高度与设计高度之比分别取0.7，0.8，0.9，1.1，1.2和1.3，列车以250 km/h的速度从1号岔位直逆向通过时，列车-道岔-桥梁系统的动力响应最大值如表1和表2所示。结果表明，系统的动力响应随桥梁高度的增大而有不同程度的减小，当桥梁高度与设计高度之比大于1.0时，列车-道岔-桥梁系统动力响应随桥梁高度增加而降低的速率减小。

5  结  论

a. 建立了列车-道岔-桥梁空间振动模型，并编制了相应的数值计算程序，研究了直逆向过岔时，列车运行速度、轨下垂向刚度、枕下垂向均布刚度、岔区垂向不平顺幅值及梁体高度对列车-道岔-连续刚构桥系统振动的影响。

b. 系统响应随列车速度和岔区垂向不平顺幅值增大、梁体高度减小而增加；轨下垂向刚度对系统不同的响应有不同的影响；道岔响应随枕下垂向均布刚度增大而降低。

c. 列车速度和岔区垂向不平顺幅值应分别控制在260 km/h和3.6 mm以内；梁体高度与设计高度之比不应小于1.0。减小轨下垂向刚度，增大枕下垂向均布刚度，均有利于降低道岔的动力响应。

参考文献：

[1] 曾志平, 陈秀方, 赵国藩. 连续梁桥上无缝道岔伸缩力与位移计算[J]. 交通运输工程学报, 2006, 6(1): 34-38.
ZENG Zhi-ping, CHEN Xiu-fang, ZHAO Guo-fan. Calculation of longitudinal force and displacement of seamless turnout on continuous beam bridge[J]. Journal of Traffic and Transportation Engineering, 2006, 6(1): 34-38.

[2] 曾志平, 陈秀方, 赵国藩. 简支梁桥上无缝道岔伸缩力与位移影响因素分析[J]. 中国铁道科学, 2006, 27(1): 53-58.
ZENG Zhi-ping, CHEN Xiu-fang, ZHAO Guo-fan. Analysis of the influence of some parameters on the temperature force and displacement of seamless turnout on simple-supported beam bridge[J]. China Railway Science, 2006, 27(1): 53-58.

[3] 王 平, 杨荣山, 刘学毅. 无缝道岔铺设于长大连续梁桥上时的受力与变形分析[J]. 交通运输工程与信息学报, 2004, 2(3): 16-19.
WANG Ping, YANG Rong-shan, LIU Xue-yi. Analysis on the influence of seamless turnout on large continuous bridge [J]. Journal of Transportation Engineering and Information, 2004, 2(3): 16-19.

[4] 刘衍峰, 高 亮, 冯雅薇. 桥上无缝道岔受力与变形的有限元分析[J]. 北京交通大学学报, 2006, 30(1): 66-70.
LIU Yan-feng, GAO Liang, FENG Ya-wei. Finite Analysis of jointless turnout on bridge [J]. Journal of Beijing Jiaotong University, 2006, 30(1): 66-70.

[5] 曾庆元, 郭向荣. 列车桥梁时变系统振动分析理论及应用[M]. 北京: 中国铁道出版社, 1999.
ZENG Qing-yuan, GUO Xiang-rong. The theory and application of train-bridge time-variant system vibration analysis[M]. Beijing: China Railway Press, 1999.

[6] XIANG Jun, ZENG Qing-yuan, LOU Ping. Theory of random energy analysis for train derailment[J]. Journal of Central South University of Technology, 2003, 10(2): 134-139.

[7] 向 俊, 杨军祥, 赫 丹, 等. 焦柳线酉水大桥上货物列车脱轨分析[J]. 中南大学学报: 自然科学版, 2006, 37(1): 169-175.
XIANG Jun, YANG Jun-xiang, HE Dan, et al. Derailment analysis of freight train on Youshui bridge on Jiaoliu line[J]. Journal of Central South University: Science and Technology, 2006, 37(1): 169-175.

[8] 向 俊, 左一舟, 赫 丹, 等. 关于列车-轨道(桥梁)时变系统空间振动方程的建立及其求解[J]. 铁道科学与工程学报, 2005, 2(1): 34-38.
XIANG Jun, ZUO Yi-zhou, HE Dan, et al. Establishment and solution to spatial vibration equation of train-track(bridge) time-varying system[J]. Journal of Railway Science and Engineering, 2005, 2(1): 34-38.

[9] 娄 平, 曾庆元. 车辆-轨道-桥梁系统垂向运动方程的建立[J]. 铁道学报, 2004, 26(5): 71-80.
LOU Ping, ZENG Qing-yuan. Formulation of equations of vertical motion for vehicle-track-bridge system[J]. Journal of the China Railway Society, 2004, 26(5): 71-80.

[10] 曾庆元, 杨 平. 形成矩阵的“对号入座”法则与桥梁空间分析的桁段有限元[J]. 铁道学报, 1986, 8(2): 48-59.
ZENG Qing-yuan, YANG Ping. The “set-in-right-position” rule for formulating matrix and the finite element method of truss section for spatial analysis of truss grider[J]. Journal of the China Railway Society, 1986, 8(2): 48-59.

[11] 曾志平. 高速铁路桥上无缝道岔伸缩力及列车-道岔-桥梁系统空间振动研究[D]. 长沙: 中南大学土木建筑学院, 2006.
ZENG Zhi-ping. Study on the tensile and compressive force of seamless turnout on bridge and train-turnout bridge system spatial vibration[D]. Changsha: School of Civil and Architectural Engineering, Central South University, 2006.

[12] 王 平. 道岔区轮轨系统动力学的研究[D]. 成都: 西南交通大学土木工程学院, 1997.
WANG Ping. Research on wheel/rail system dynamics on turnout [D]. Chengdu: School of Civil Engineering, Southwest Jiaotong University, 1997.

[13] 任尊松. 车辆-道岔系统动力学研究[D]. 成都: 西南交通大学列车与线路研究所, 2000.
REN Zun-song. Study on vehicle-turnout system dynamics[D]. Chengdu: Train & Track Research Institute, Southwest Jiaotong University, 2000.

[14] 赵国堂. 秦沈客运专线道岔区轨道不平顺的分布特征[J]. 中国铁路, 2003, 41(1): 46-51.
ZHAO Guo-tang. Distribution features of track irregularity in the switch area on the Qinhuangdao-Shenyang dedicated passenger line[J]. Chinese Railways, 2003, 41(1): 46-51.

[15] 铁道科学研究院. 秦沈客运专线38号道岔综合试验[R]. 北京: 铁道科学研究院, 2003.
China Academy of Railway Science. Comprehensive experiment of No.38 weldless turnout on the Qinhuangdao-Shenyang dedicated passenger line[R]. Beijing: China Academy of Railway Science, 2003.

收稿日期：2007-10-25；修回日期：2008-02-20

基金项目：铁道部科技开发计划项目(2004G05-A)

通信作者：曾志平(1975-)，男，湖南宁乡人，博士后，从事道路与铁道工程研究；电话：13203138358；E-mail: hzzp7475@126.com