DOI: 10.11817/j.ysxb.1004.0609.2020-35852
管材缩径起皱失稳数值模拟
张 鑫,赵长财,杜 冰,李 晗,韩兆建,宋鹏飞
(燕山大学 先进锻压成形技术与科学教育部重点实验室,秦皇岛 066004)
摘 要:轻质薄壁件越来越多地应用于航空、航天和汽车等高新技术工程领域,但起皱失稳一直是薄壁件成形过程中主要的缺陷之一。因此,轻质薄壁件成形过程中的塑性失稳起皱预测研究就显得尤为重要。本文针对塑性成形中薄壁管件结构由于存在多种初始缺陷(如厚度不均,尺寸偏差等)从而导致失稳模拟预测与实际情况不符的现象,以AA6061固体颗粒介质管材缩径工艺为算例,结合ABAQUS中最适合复杂接触工况的DYNAMIC算法以及Draker-Pager颗粒介质成形数值模拟模型,对无初始缺陷圆柱壳体、引入屈曲模态初始缺陷圆柱壳体、引入厚度不均初始缺陷圆柱壳体以及同时引入屈曲模态和厚度不均缺陷的圆柱壳体进行了缩径成形模拟,将四种条件下的管件失稳波形模拟结果与试验结果进行了比较。结果表明:同时引入屈曲模态和厚度不均缺陷的动态显示有限元法可以准确预测出管材缩径失稳后的形貌,并将模拟仿真与实验的应力-位移曲线进行对比,验证了此模拟方法的可靠性。
关键词:管材缩径;起皱失稳数值模拟;屈曲模态;厚度缺陷
文章编号:1004-0609(2020)-08-1855-11 中图分类号:TG386.43 文献标志码:A
薄壁件由于其轻量化、强韧化、柔性化等优点,越来越多的用于航空航天、汽车、化工等技术领域。压缩引起的起皱失稳除影响成形件的质量、精度和成形极限外,还直接影响一些成形工序能否顺利进行,是薄壁件成形过程中的主要缺陷和障碍之一。因此,如何准确有效地预测和控制塑性失稳起皱现象,从而实现薄壁件的精确塑性成形,并提高其成形极限和成形质量成为塑性加工领域的研究热点问题[1-2]。
很多学者对起皱现象进行了大量研究。试验方法如YOSHIDA[3]提出的YBT试验(YBT-Yoshida Buckling Test),理论解析如CAO[4]提出的能量法、HILL[5]提出的分岔理论等。然而这些方法对于研究某些成形起皱失稳问题而言局限性较大。以管材缩径过程为例,管件成形过程中封闭于模具型腔内部,只有成形结束从模具内取出后才能观测其最终的起皱形貌,难以实时监测起皱发生、发展过程,不利于失稳规律的研究。在理论解析过程中,由于对成形各方面条件的高度简化,在分析结果适用性上受到了较大质疑。因此,数值模拟方法无疑是最适合研究管材缩径成形问题的方法。在管板材起皱失稳数值模拟预测方面,已有一些可靠性得到公认的方法,如RUST等[6]基于ANSYS平台,通过“植入”屈曲模态作为结构的初始缺陷,成功模拟出长臂伸缩望远镜的结构失稳起皱问题。WONG等[7]通过ABAQUS的BUCKLE模块,将特征值屈曲分析获得的薄膜结构的各阶屈曲模态通过不同方式组合定义为几何微缺陷,成功监测到波纹的产生过程,并与试验结果对比,吻合较好。CAO等[8]利用有限元分析和能量法相结合准确地预测出拉深成形过程中圆锥件侧壁起皱及盒形件法兰起皱的情况,给出板材成形中起皱的新判据。LI等[9-10]通过能量原理和有限元相结合的方法,开发一种薄壁管弯曲起皱预测模型,获得了多工具约束下各种界面处的间隙和摩擦对起皱不稳定性的影响。
市面上绝大多数轧制、挤压和焊接管坯均存在形状和壁厚缺陷,而缺陷是影响管材失稳起皱的关键因素之一。KOITER等[11]率先利用混合摄动-伽辽金法研究了轴对称厚度缺陷对轴向压缩下圆柱壳屈曲的影响。GUSIC等[12]通过有限元分岔分析研究了外压下圆周方向厚度变化对薄壁圆柱壳屈曲的影响。COMBESCURE等[13]利用COMI轴对称壳单元分析了外压作用下几何缺陷和周向厚度缺陷对薄壁圆柱壳的影响。LIU等[14-15]以大直径薄壁铝合金管为研究对象,结合初始缺陷和显式动态算法通过引入微缺陷对显式有限元模型进行扰动,预测了多模具约束下数控弯管的塑性起皱问题。
管材外压缩径成形工艺不同于常规的薄壁件成形工艺。管材厚度远小于其他方向尺寸,面内环向方向始终受到压应力的作用,成形区极易进入失稳状态,而成形过程中由于管坯被模具包裹,缩径规律难以实时观测。由于成形难度大,试验和理论分析手段受限,相关的缩径类管件的实际应用产品较少,开发和研究潜力巨大。成形过程中的很多关键问题都有待通过科学的探究手段去解决。本文以AA6061管件固体颗粒介质缩径试验结果为参照依据,通过比较不同的起皱失稳有限元数值模拟方法的分析结果,对管坯无法避免的壁厚缺陷影响下的起皱失稳形貌进行了考证,证实了厚度缺陷对管材起皱失稳的影响不可忽略,得出了可用于预测有初始几何缺陷的管坯零件成形过程中起皱失稳现象的最佳仿真方法。
1 管材缩径试验研究
本文选用固体颗粒介质成形工艺方法进行缩径试验,固体颗粒介质成形(Solid granule medium forming,简称SGMF)工艺以固体颗粒为传压介质,代替现有软模成形工艺中液体、气体或黏性介质对板管材进行成形,由于固体颗粒相比其他成形介质,具有易于密封,方便填充,介质承压性能强和热稳定性好等优点,该成形工艺在某些方面具有其独特的优势。固体颗粒介质缩径成形工艺模具图和原理示意图如图1所示。
试验管坯选用长90 mm、直径100 mm、厚度1.2 mm的AA6061铝合金挤压管段。DU等[16-17]通过理论和试验研究证明管材外压缩径成形工艺中同等成形几何条件下,母材管坯比固溶软化后的管坯的抗皱性能强。本文为使成形件褶皱形貌更加明显,便于对比起皱后的轮廓曲线,对管坯进行500 ℃+2.5 h的固溶处理,然后进行缩径工艺试验。通过改变垫片数量得到缩径区高度h为25 mm、35 mm和45 mm的成形件,如图2所示。
为了提取成形零件的轮廓形状,使用图3所示的HandySCAN三维激光扫描仪对成形零件进行全面扫描,获得其三维点云数据,并将云图导入CATIA软件进行逆向重构,输出的三维CAD图形及缩径区间中间截面轮廓曲线如图4所示。

图1 模具照片及缩径工艺原理示意图
Fig. 1 Die photo (a) and schematic diagram (b) of principle of SGMF tube outer pressure compression forming

图2 不同缩径区高度的成形零件图
Fig. 2 Forming parts of different diameter reduction zones

图3 HandySCAN三维激光扫描仪
Fig. 3 HandySCAN 3D laser scanner
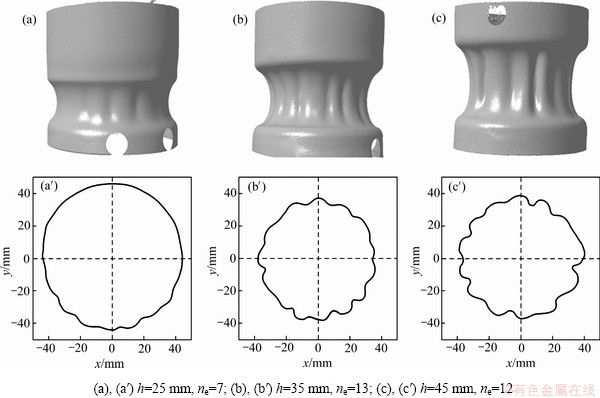
图4 不同缩径高度成形零件的逆向三维图和变形区中间截面轮廓图(ne为失稳波数)
Fig. 4 Reverse 3D diagram and intermediate section profile of parts formed with different height of diameter reduction zones (ne is instability wave number)
2 管材缩径有限元模拟模型建立
2.1 材料属性
沿管材纵向切取图5中的拉伸试样进行单向拉伸试验,得到母材和经过(500 ℃,2.5 h)固溶处理后试件的应力-应变曲线,如图5所示。从图5可以看出,经过固溶处理后试件伸长率大幅提高,而屈服强度大幅降低。本文模拟中选用AA6061铝合金挤压管材经过(500 ℃,2.5 h)固溶处理后的应力-应变曲线,其他力学性能参数如密度ρ、弹性模量E、泊松比ν、屈服强度σs和伸长率A,如表1所示。
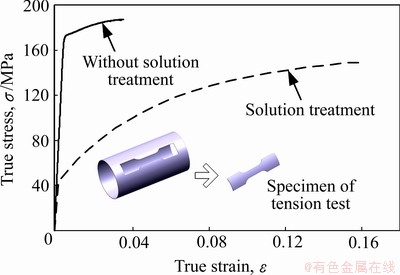
图5 AA6061管材真实应力-应变曲线
Fig. 5 Axial true stress-strain curves of AA6061 tube
表1 AA6061铝合金管材经过(500 ℃,2.5 h)固溶处理后的力学性能参数
Table 1 Mechanical properties of AA6061 tube under solution treatment at (500 ℃,2.5 h)

ABAQUS 中的线性Drucker-Prager模型可以较为真实的模拟散体介质所表现出的力学性能,试验中采用非金属固体颗粒介质,即GM颗粒作为传压介质[18],本课题组通过单向压缩和剪切实验得到GM颗粒的Drucker-Prager模型参数[19],如表2所示。
表2中β为颗粒介质的内摩擦角;EGM为颗粒介质弹性模量;ν为颗粒介质的泊松比;Х为三轴拉伸屈服应力与三轴压缩屈服应力之比;ψ为颗粒介质的减胀角。
表2 GM颗粒Drucker-Prager模型参数
Table 2 Drucker-Prager model parameters for GM

2.2 网格划分和接触条件
管坯采用四节点线性缩减积分壳单元,即S4R 单元,其性能稳定,适用于薄壳和中等厚度壳体结构,并且能很好地模拟大变形、大应变等非线性行为,在研究失稳问题时具有较高的准确性。颗粒介质采用八节点线性减缩积分实体单元,即S3D8R单元。其余部件均定义为刚体。管坯管端固定,对冲头施加轴向位移。有限元模型如图6所示。
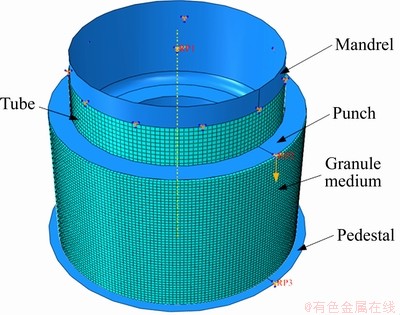
图6 管材缩径成形数值模型
Fig. 6 Numerical model of tube diameter reduction forming
3 管材缩径有限元模拟方法分析
随着计算机技术的提高和有限元软件的高速发展,数值模拟方法成为解决起皱失稳问题的主要工具。目前,用于处理薄壁件失稳问题的数值模拟算法主要有静力隐式有限元法和动力显式有限元法。其中静力有限元分析方法又分为线性(特征值)屈曲分析和非线性屈曲分析(弧长法)[20]。然而,这两种方法无法用于预测类似于管材缩径起皱类的问题。因为特征值屈曲分析通常用于评估刚性结构的临界屈曲载荷,也可以为几何缺陷模型的建立提供各种屈曲模态,但是难以处理具有材料、几何非线性的塑性变形行为;弧长法用弧长量代替时间量,可以考虑几何、材料等非线性因素,可用于评估结构的最大临界载荷及后屈曲状态,但对于复杂接触边界条件的情况,容易出现求解不收敛问题[20]。用于模拟塑性成形最普遍使用的动力显示有限元算法基于动力学方程,不需求解切线刚度矩阵,也不需进行平衡迭代,因此不存在收敛性的问题,常用于分析动态事件、复杂接触和大变形问题,但是该算法获得的起皱波纹是通过迭代误差产生的,并非真正意义上的失稳皱纹。因为动力显式算法中没有求解系统刚度矩阵的步骤,因此不能检测出失稳分叉点,须与其他方法相结合使用来预测起皱失稳[21]。
以缩径区高度h=35 mm为例,单纯采用动态显示有限元法进行模拟得到如图7所示的结果,可以看出管材缩径后并未像实验结果所观察到的那样出现起皱失稳现象。
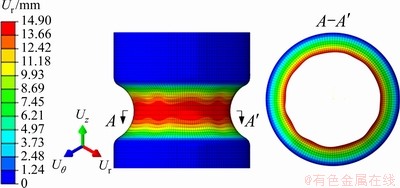
图7 管材缩径动态显示有限元法模拟图
Fig. 7 Dynamic finite element simulation diagram of tube diameter reduction
为将动态显示有限元算法在模拟非线性、复杂接触下的成形问题的特有优势运用到失稳问题的计算上,本文通过引入初始缺陷,对显示有限元模型进行扰动,从而实现了对复杂接触条件下管材缩径成形工艺中起皱的预测。
可用作初始缺陷来扰动理想网格的对象有很多种,如屈曲模态、厚度不均度、材质不均度等。由于存在于管材内部的夹杂物、孔洞等物理缺陷随机性和分散性很强,材质不均度不易表述和测量,无法在模拟中体现,因此本文就对植入屈曲模态和厚度不均度的模拟结果进行分析。
3.1 屈曲模态初始缺陷
特征值屈曲分析(屈曲模态分析)实质是一种线性摄动求解方法,以寻找模型刚度矩阵变得奇异的载荷,即式(1)[22]具有非无效解。
 (1)
(1)
式中:KMN为施加载荷时的刚度矩阵;νM为非无效位移解。
通过式(2)[22]可以得到特征值和特征向量。
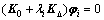 (2)
(2)
式中:K0为对应于基础状态的刚度矩阵;KΔ为对应于递增载荷的微分初始应力和载荷刚度矩阵;λi为特征值;φi为屈曲模态形状(特征向量);i为第i阶屈曲模态。
特征值屈曲分析所得到的屈曲模态即为结构可能的失稳模态。缺陷Dxi具有如下形式:
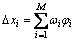 (3)
(3)
式中:ωi为相应的比例因子;M为特征向量的阶数。
本文通过第2部分建立管材缩径有限元模型后对“理想”结构进行特征值屈曲分析,获得前20阶屈曲模态,特征值见表3。
表3 屈曲模态特征值
Table 3 Eigenvalues of buckling modes
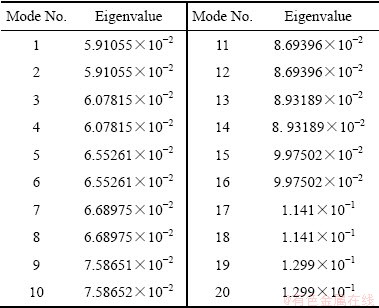
在利用屈曲模态作为初始缺陷引入动态显示模拟分析起皱失稳时,通常将最低阶屈曲模态引入理想几何模型中扰动网格,但是对于薄壁短管结构而言,由表3可知特征值几乎相等,难以直接判断最低阶特征模态是否起主导作用。对此,LIU等[14]在薄壁管数控绕弯成形过程中,根据铁木辛柯能量法,将嵌入缺陷模型中变形消耗的能量最小的初始缺陷定义为合理初始缺陷。为便于计算,将有限元模拟结果的弹性应变能和塑性耗散能之和定义为消耗的总能量。对于缩径成形,第i(i=1、3、5…19)阶模态和第i+1阶模态特征值相等,屈曲形貌的波数相等,嵌入理想几何模型进行模拟后消耗的总能量也相等,为节省计算成本,本文将第i(i=1、3、5…19)阶模态嵌入理想几何模型,得到嵌入不同阶模态后模型所消耗的总能量如图8所示。由图8可看出,引入不同模态初始缺陷对模型消耗总能量的影响不大,无法直接判断第几阶模态是最合理的初始缺陷,因此,本文选择失稳波数与实际起皱波数相等,波形相似的第19阶模态进行分析。
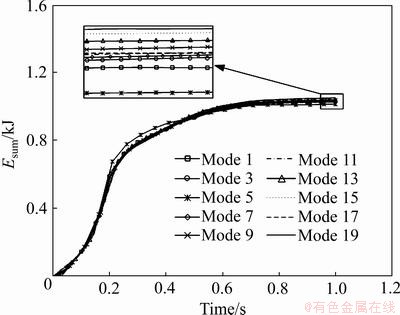
图8 不同模态缺陷模型所消耗的能量
Fig. 8 Energy consumed by different modal defects
特征值屈曲分析输出的壳体第19阶屈曲模态的径向位移云图如图9所示。
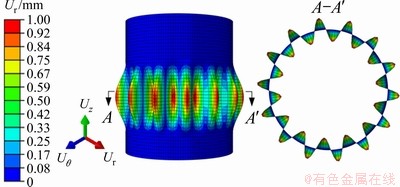
图9 第19阶屈曲模态径向位移云图
Fig. 9 Radial displacement nephogram of 19th buckling mode
将默认全局系统中的第19阶屈曲模态写入结果文件作为节点数据,并在后续Dynamic-explicit分析中,保持网格模型和边界条件与*Buckle分析步一致,通过*IMPERFECTION命令,将初始缺陷缩放后嵌入网格模型。在缺陷缩放比例因子ω的选择上,较大的缩放比例因子肯定会使屈曲过程过渡的更加平滑,但另一方面,也可能会使结果脱离实际。经验而言,用于不同屈曲模态的缺陷缩放比例因子ω最大只需相应结构尺寸(如管厚)的百分之几便足够诱发屈曲的产生和发展。本文结合经验值范围和真实实验数据,确定缺陷缩放比例因子ω=0.01。最终得到植入屈曲模态后管材缩径成形的模拟图如图10所示。
由图10可以看出植入屈曲模态缺陷后,动态显示有限元法可以模拟出管材缩径的失稳起皱问题,但得到均匀的失稳皱纹,与试验结果中皱纹的几何形貌存在差别。这是由于植入屈曲模态缺陷是为了通过预埋分叉路径实现对“理想”管材起皱失稳的诱发,但是并未考虑实际管材的厚度缺陷所可能导致的波纹非均匀分布的现象
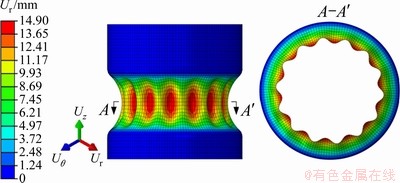
图10 植入屈曲模态的缩径成形模拟图
Fig. 10 Reduced-diameter forming simulation diagram by introduced buckling modes
3.2 厚度不均缺陷
实际工程中,薄壁管件由于制造工艺等因素常常存在壁厚缺陷。这些缺陷会对管材缩径起皱产生很大影响。本文在有限元建模中赋予“理想”壳体不同的厚度场,作为初始厚度不均缺陷。分别研究了线性变壁厚、抛物线式变壁厚和余弦式变壁厚三种厚度缺陷对圆柱壳缩径起皱的影响。
以试验试件壁厚实测值为依据,在相等的厚度幅值情况下,比较厚度随环向角坐标呈线性变化、抛物线式变化和余弦式变化三种情况下的试件起皱失稳规律,相对应的壁厚分布函数如式(4)、(5)、(6)所示。
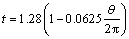 (4)
(4)
 (5)
(5)
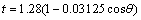 (6)
(6)
式中:t表示圆柱壳的实际厚度,θ(-π<θ<π)是圆柱壳的环向角坐标。三种圆柱壳厚度变化规律如图11所示。
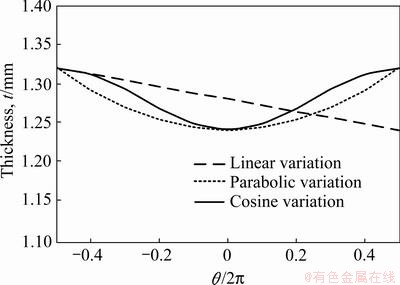
图11 圆柱壳三种形式的厚度变化规律
Fig. 11 Thickness variation of cylindrical shells in three forms
将三种厚度缺陷赋予“理想”管材进行模拟,输出管材缩径后的形状和变形区中间截面的失稳波形节点坐标绘图,模拟得到的波数用ns表示,如图12所示。从图12可以看出,赋予厚度缺陷的管材,通过动态显示算法可以模拟出实际管材缩径过程中的起皱波形不对称问题。结合图11,可以得出当厚度幅值相等时,抛物线式厚度缺陷引起的失稳起皱波形相较于线性厚度缺陷和余弦式厚度缺陷下的起皱波形不甚明显,失稳后得到的波数较少。这是由于不同厚度的区域承载能力不同,薄的地方承载能力小,会率先失稳产生皱纹,厚度变化程度越大,起皱先后时刻相差越大,褶皱越不容易展开。而抛物线式的厚度变化更为平缓,波形易于展开。
虽然理想网格模型被赋予厚度缺陷后会改变管坯的轴对称失稳特征,呈现出新的失稳形貌,但是得到的失稳波形和波数均与缩径试验存在较大差异,只引入厚度不均缺陷也无法准确预测管材缩径起皱失稳问题。
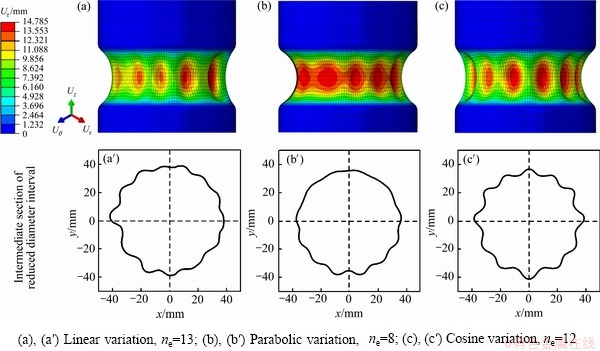
图12 三种厚度缺陷模拟结果对比图
Fig. 12 Comparison of simulation results of three thickness defects
3.3 两种缺陷叠加
因为实验中所用管坯存在厚度不均的现象,为了和模拟实验中管材缩径的实际起皱情况相吻合,本文尝试将屈曲模态初始缺陷和厚度不均缺陷同时引入“理想”模型,以实现对管材缩径起皱的准确预测。现将试验所用的管材沿环向18等分,分别测量壁厚,三次测量后取平均值,再将所测数据进行拟合,拟合公式如式(7)所示。图13为管材环向壁厚分布曲线。
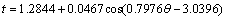 (7)
(7)
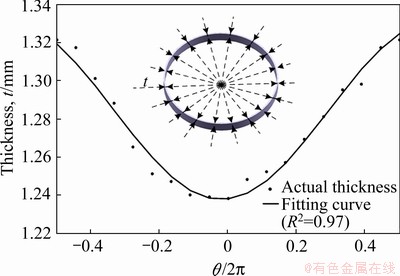
图13 管材环向壁厚分布曲线
Fig.13 Circumferential wall thickness distribution curve of the tube
将拟合公式(7)所表示的厚度变化作为厚度缺陷,和与实际起皱波数相等的第19阶屈曲模态作为模态缺陷,一起引入“理想”管材模型中,按图14所示的流程进行模拟。
最终得到的模拟结果与实验结果对比如图15(a)所示。由图15(a)可以看出,同时引入模态缺陷和厚度缺陷的模拟结果与实验后管件的失稳形貌和起皱波数较为吻合。这是因为模态缺陷预埋分叉路径,诱发理想管材失稳,厚度缺陷影响波纹高度和波纹大小,使模拟中管材变形情况与实际中的管材缩径更为贴合。
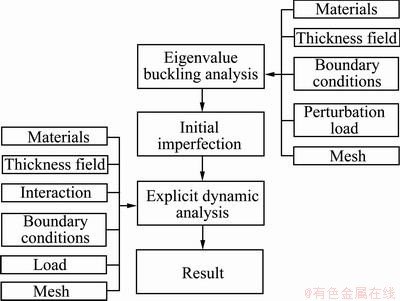
图14 管材缩径有限元模拟预测流程图
Fig. 14 Finite element simulation forecast diagram of tube diameter reduction
为排除模拟的偶然性,本文又利用此方法分别模拟了缩径区高度为45 mm和25 mm的两种情况。得到的失稳形貌对比图如图15(b)、(c)所示。
由图15(b)、(c)可以看出,缩径区高度为45 mm和25 mm时,仿真模拟结果与实验结果吻合较好,验证了利用将屈曲模态缺陷和厚度缺陷引入“理想”模型中的动态显示有限元法分析研究管材缩径失稳起皱的可行性。
4 力-位移曲线对比
管材缩径成形过程中,管件包在模具内部,无法实时观测起皱情况,相关数据采集也比较困难。为进一步验证本文提出的管材缩径模拟方法的可靠性,将试验过程中压机输出的力-位移曲线与数值模拟的曲线进行对比,对比结果如图16所示。
由图16可以看出,模拟与试验的力-位移曲线有所差别,这主要是由于试验过程中固体颗粒体积压缩导致的。试验曲线在管材缩径过程前期力随位移增长的幅度较为缓慢,随后缩径管件充型贴膜,增幅变大,与数值模拟的力-位移曲线增长趋势基本一致。因此可以证明本文数值模拟方法的可靠性。

图15 管材缩径实验和模拟形状对比图和变形区中间截面轮廓对比图
Fig. 15 Experimental and simulation comparison of tube shape and intermediate section profile of deformation zone
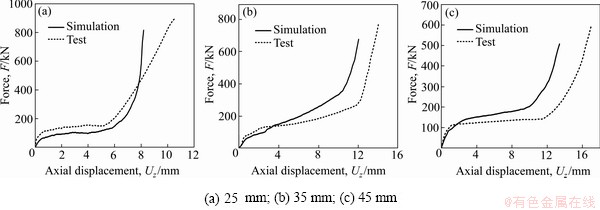
图16 不同缩径区高度的力-位移曲线模拟与试验对比图
Fig. 16 Comparisons between simulation and test of force-displacement curves with different diameter reduction heights
5 结论
1) 基于Drucker-Prager模型假设,单纯使用无初始缺陷的动态显示有限元法无法捕捉到管材起皱失稳分叉点,模拟不出管材缩径后的失稳形貌。
2) 单独引入乘以比例因子的初始屈曲模态作为网格微缺陷的模拟方法,提高了管材对失稳分叉点的敏感性,可以预测管材失稳形貌,但与试验结果偏差较大。
3) 厚度缺陷可以对管材失稳形貌产生影响,薄的地方率先失稳且波形幅度变化较大。当厚度幅值相等时,线性变壁厚和余弦式变壁厚的起皱波动比抛物线式变壁厚明显,失稳后得到的波数较多。
4) 采用同时引入模态缺陷和厚度缺陷的动态显示算法可以准确预测出管材缩径失稳后的形貌。验证了固体颗粒介质管材缩径工艺模拟的准确性。
REFERENCES
[1] LIU Nan, YANG He, LI Heng, YAN Si-liang. Plastic wrinkling prediction in thin-walled part forming process: A review[J]. Chinese Journal of Aeronautics, 2016, 29(1): 1-14.
[2] 李 恒, 杨 合, 詹 梅, 林 艳, 谷瑞杰. 薄壁件塑性成形失稳起皱的国内外研究进展[J]. 机械科学与技术, 2004(7): 837-842.
LI Heng, YANG He, ZHAN Mei, LIN Yan, GU Rui-jie. A review of the research on wrinkling in thin-walled parts plastic forming processes[J]. Mechanical Science and Technology, 2004(7): 837-842.
[3] YOSHIDA K. Purposes and features of the Yoshida wrinkling test[J]. Journal of the JSTP, 1983, 24(272): 901-908.
[4] CAO J. Prediction of plastic wrinkling using the energy method[J]. Journal of Applied Mechanics, 1999, 66(3): 646–652.
[5] HILL R. A general theory of uniqueness and stability in elastic-plastic solids[J]. Journal of the Mechanics & Physics of Solids, 1958, 6(3): 236-249.
[6] RUST W, SCHWEIZERHOF K. Finite element limit load analysis of thin-walled structures by ANSYS (implicit), LS-DYNA (explicit) and in combination[J]. Thin-walled structures, 2003, 41(2/3): 227-244.
[7] WONG W, PELLEGRINO S. Wrinkled membranes Ⅲ: Numerical simulations[J]. Journal of Mechanics of Materials and Structures, 2006, 1(1): 63-95.
[8] CAO J, BOYCE M C. Wrinkling behavior of rectangular plates under lateral constraint[J]. International journal of solids and structures, 1997, 34(2): 153-176.
[9] LI Heng, YANG He, ZHAN Mei, GU Rui-jie. A new method to accurately obtain wrinkling limit diagram in NC bending process of thin-walled tube with large diameter under different loading paths[J]. Journal of Materials Processing Technology, 2006, 177(1/3): 192-196.
[10] LI Heng, YANG He, ZHAN Mei. A study on plastic wrinkling in thin-walled tube bending via an energy-based wrinkling prediction model[J]. Modelling and Simulation in Materials Science and Engineering, 2009, 17(3): 35007-35039.
[11] KOITER W T, ELISHAKOFF I, LI Y W, STARNES J H. Buckling of an axially compressed cylindrical shell of variable thickness[J]. International Journal of Solids and Structures, 1994, 31(6): 797-805.
[12] GUSIC G, COMBESCURE A, JULLIEN J F. The influence of circumferential thickness variations on the buckling of cylindrical shells under external pressure[J]. Computers & Structures, 2000, 74(4): 461-477.
[13] COMBESCURE A, GUSIC G. Nonlinear buckling of cylinders under external pressure with nonaxisymmetric thickness imperfections using the COMI axisymmetric shell element[J]. International Journal of Solids & Structures, 2001, 38(34): 6207-6226.
[14] LIU Nan, YANG He, LI Heng, TAO Zhi-jun, HU Xiao. An imperfection-based perturbation method for plastic wrinkling prediction in tube bending under multi-die constraints[J]. International Journal of Mechanical Sciences, 2015, 98: 178-194.
[15] LIU Nan, YANG He, LI Heng, ZHAN Mei, TAO Zhi-jun, HU Xiao. Modelling of wrinkling in NC bending of thin-walled tubes with large diameters under multi-die constraints using hybrid method[J]. Procedia Engineering, 2014, 81: 2171-2176.
[16] 杜 冰, 谢 军, 关风龙, 张 鑫, 赵长财. 金属薄壁管件外压缩径成形理论及实验研究[J]. 中国有色金属学报, 2018, 28(3): 586-593.
DU Bing, XIE Jun, GUAN Feng-long, ZHANG Xin, ZHAO Chang-cai. Theory and experimental research on outer pressure compression forming of thin metal tube part[J]. The Chinese Journal of Nonferrous Metals, 2018, 28(3): 586-593.
[17] 杜 冰, 关风龙, 张 鑫, 谢 军, 赵长财. 基于管材缩径工艺的薄壁件成形起皱失稳共性规律研究[J]. 燕山大学学报, 2017, 41(6): 510-515.
DU Bing, GUAN Feng-long, ZHANG Xin, XIE Jun, ZHAO Chang-cai. Study on common rules in wrinkling instability of thin-walled parts forming based on tube outer pressure compression technology[J]. Journal of Yanshan University, 2017, 41(6): 510-515.
[18] 杜 冰, 赵长财, 李雪峰, 何 昕, 董国疆. 高温合金凸环管件固体颗粒介质成形工艺[J]. 中国有色金属学报, 2014, 24(7): 1721-1729.
DU Bing, ZHAO Chang-cai, LI Xue-feng, HE Xin, DONG Guo-jiang. Forming technology of high temperature alloy convex ring shaped tube by solid granule medium[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(7): 1721-1729.
[19] DONG Guo-jiang, ZHAO Chang-cai, CAO Miao-yan. Flexible-die forming process with solid granule medium on sheet metal[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(9): 2666-2677.
[20] 杜 冰, 关风龙, 宋鹏飞, 韩兆建, 张 鑫, 赵长财. 薄板起皱失稳数值模拟计算方法[J].机械工程学报, 2018, 54(24): 42-50.
DU Bing, GUAN Feng-long, SONG Peng-fei, HAN Zhao-jian, ZHANG Xin, ZHAO Chang-cai. Numerical simulation methods of sheet metal wrinkling[J]. Journal of Mechanical Engineering, 2018, 54(24): 42-50.
刘 楠. 复杂边界条件下薄壁件塑性成形失稳起皱预测[D]. 西安: 西北工业大学, 2015: 62-63.
LIU Nan. Instability and wrinkling prediction in plastic forming processes of thin-walled parts under complex boundary conditions[D]. Xi'an: Northwestern Polytechnical University, 2015: 62-63
[21] SIMULIA D S. ABAQUS6.14 Help Documentation[Z]. 2014.
Numerical simulation on wrinkling instability of tube outer pressure compression
ZHANG Xin, ZHAO Chang-cai, DU Bing, LI Han, HAN Zhao-jian, SONG Peng-fei
(Key Laboratory of Advanced Forging & Stamping Technology and Science of Ministry of Education, Yanshan University, Qinhuangdao 066004, China)
Abstract: The lightweight thin-walled parts are increasingly used in high-tech engineering fields such as aviation, aerospace and automobile. Wrinkling instability has always been one of the major defects in thin-walled parts forming processes. Therefore, the study on prediction of plastic wrinkling instability becomes particularly important in the process of forming lightweight thin-walled parts. Based on the inconsistent between the instability simulation prediction of thin-walled tube structures and the actual situation which are due to various initial defects (such as uneven thickness, dimensional deviations, etc.), this paper takes the example of the AA6061 diameter-reduced tubes by solid granule medium forming technology and combines the DYNAMIC algorithm which is the most suitable for complex contact conditions in ABAQUS, simulates the tube outer pressure compression forming with no initial imperfections, buckling modes initial imperfections, uneven thickness initial imperfections and the last one which contains buckling modes initial imperfections and uneven thickness initial imperfections. The dynamic finite element method with simultaneous introduced buckling modes and thickness unevenness imperfections can accurately predict the instability waveforms of the tube through the comparison between the simulations and the tests. The reliability of the simulation method is verified through the comparison between the simulative and experimental force-displacement curves.
Key words: tube outer pressure compression forming; numerical simulation of wrinkling instability; buckling mode; thickness imperfection
Foundation item: Projects(51605420, 51775481) supported by the National Natural Science Foundation of China; Project(E2018203143) supported by the Natural Science Foundation of Hebei Province, China
Received date: 2019-08-26; Accepted date: 2019-12-22
Corresponding author: DU Bing; Tel: +86-13784508057; E-mail: pangpang115@163.com
(编辑 何学锋)
基金项目:国家自然科学基金资助项目(51605420,51775481);河北省自然科学基金资助项目(E2018203143)
收稿日期:2019-08-26;修订日期:2019-12-22
通信作者:杜 冰,副教授,博士;电话:13784508057;E-mail:pangpang115@163.com