J. Cent. South Univ. Technol. (2011) 18: 465-472

DOI: 10.1007/s11771-011-0719-1

A novel deadline and budget constrained scheduling heuristics for computational grids

WANG Yong(王勇)¹, R. M. BAHATI², M. A. BAUER²

1. School of Computer Science, China University of Geosciences, Wuhan 430074, China;

2. Department of Computer Science, University of Western Ontario, Ontario N6A 5B7, Canada

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: The conventional deadline and budget constrained (DBC) scheduling heuristics for economic-based computational grids does not take the inconsistency of grid heterogeneity into account, which can lead to decline of application completion ratios. Motivated by this fact, a novel DBC scheduling heuristics was proposed to deal with sequential workflow applications. In order to valuate the inconsistency, the relative cost (RC) metric was introduced, which was used to indicate the task-starving degree for resources. The new algorithm assigns tasks to resources, considering completion time, budget and RC together. The GridSim toolkit and the benchmark suites of the standard performance evaluation corporation (SPEC) were used to simulate the heterogeneous grid environment and applications. The experimental results show that the task and workflow completion ratios of the new heuristics are higher than those of the conventional heuristics.

Key words: computional grids; economic-based grid; grid brocker; grid scheduling; simulation

1 Introduction

Grid computing has become an increasingly popular solution to optimizing resource allocation and integrating various computing resources in highly charged IT environments. To this end, significant research efforts have been made towards approaches to resources sharing within an increasingly dynamic and heterogeneous computing environment. Globus is one of the most famous grid projects to provide a software infrastructure that enables applications to handle distributed heterogeneous computing resources as a single machine [1]. Resource management and scheduling (RMS), as the heart of these grid projects, is responsible for discovering, allocating, and negotiating the use of services offered by resources.

At its core, RMS allows grid users to request the allocation of one or more resources for a specific purpose and the scheduling of application problems in the appropriate resources. Within computational grids, such  problems are refer to as computational tasks, jobs, or workflows composed of tasks. The resources are referred to as data or processing units and include clusters or super computers [2]. Jobs scheduling within computational grid systems is a complex task due to a variety of factors such as geographical distance, site autonomy, domain size and dynamic characteristics of resources. Moreover, grid resources may belong to different administrative domains that are managed by proprietary policies. Grid users may also have various qualities of service (QoS) criteria such as operating system, system architecture, processing power, and/or bandwidth. So, the scheduling problem has been shown, in general, to be a NP-complete problem [3]. Thus, the development of techniques for finding near-optimal solutions for the mapping problem is an active area of research.

The evaluation of the performance of grid scheduling highly depends on the given scenario, the provider, and user objectives. The conventional scheduling scheme in grid computing allocates computing resources to tasks with the goal of optimizing a certain objective function, e.g., minimizing the makespan of tasks. This, in contrast to the conventional style is the economy-based scheduling scheme where users adopt the strategy of executing their tasks at low cost and resource providers pursue the strategy of maximizing their profits and resource utilization. In general, conventional scheduling methods utilize heuristics to assign jobs to the grid resources. Economy- based methods, on the other hand, add a market approach to the conventional scheme by charging the users for the services that they consume. The economic approach for managing resource allocation in grid environments provides a fair basis in successfully managing decentralization and heterogeneity [4].

In this work, a new deadline and budget constrained (DBC) scheduling heuristics in economy-based computational grids was proposed, which maps tasks to resources by considering not only time and cost but also relative cost (RC).

2 Related work

The design of scheduling algorithms in grid computing is complicated by the sheer magnitude of grid systems as well as the variety of non-trivial factors in grid scheduling. Traditional parallel scheduling algorithms for high performance computing, for example, cannot meet the needs of grid computing [5]. Thus, new scheduling algorithms and strategies that take into account of the characteristics of grids must be researched.

Grid scheduling has recently become a popular issue in grid computing research. BRAUN et al [6] provided a comparison of 11 static heuristics for scheduling in grid environments, which are opportunistic load balancing, minimum execution time, minimum completion time, min-min, max-min, duplex, genetic algorithm, simulated annealing, genetic simulated annealing, tabu, and A*. This study has shown that for the cases studied, the relatively simple min-min heuristics performs well in comparison with the other techniques. KIM et al [7] studied eight dynamic mapping schemes: max-max, max-min, min-min, queuing table, sufferage, slack sufferage, switching algorithm, and percent best. The priorities, deadlines, and dynamic arrival of tasks were considered in their study. When loose deadlines are used, the max-max heuristics and the slack sufferage heuristics perform the best. When tight deadlines are used, the performance of all heuristics is degraded.

The methods discussed above are all conventional scheduling methods. In contrast, market based scheduling strategies models the completion of entire jobs or tasks according to some agreed performance metric such as the cost of computation or completion time. SHETTY et al [8] surveyed various projects supporting market oriented distribution computing. There has been significant work in various aspects of market-based approaches, while there is still a lot of potential for more research. Finding optimal heuristics for task scheduling in economy-based grid is still an open problem.

VENUGOPAL and BUYYA [9] presented an algorithm for the scheduling of distributed data-intensive bag-of-task applications on data grids, which has costs associated with requesting, transferring, and processing datasets. Each of the tasks within the application depends on multiple datasets that may be distributed anywhere within the grid. Also, there are economic costs associated with the movement and the processing of datasets on distributed resources. FENG et al [10] proposed an easy-implemented algorithm to schedule the dependent tasks with some communications. The algorithm is able to meet the users’ quality of service (QoS) requirements and minimize the combination of costs and time consumed by the users’ programs. However, these studies do not aim at workflow applications. SINGH et al [11] presented a multi-objective genetic algorithm (GA) formulation for provisioning resources for an application using a slot-based resource model to optimize the cost and performance. The approach shows promising results when the resources are under high utilization or the applications have significant resource requirements. Moreover, WIECZOREK et al [12] considered multiple scheduling criteria for workflow applications modeled as directed acyclic graphs (DAGs) and investigated heuristics that allows the scheduling  of nodes of the DAG (or tasks of a workflow) onto resources. Their research can satisfy a budget constraint and get optimal overall time. However, due to the time consuming nature of GA, these heuristics are not suitable for online scheduling [13].

Our novel heuristics shows similarities with the cost, time, and cost-time optimization heuristics presented by BUYYA et al [13], and GARG et al [14]. BUYYA et al [13] aimed at minimizing the cost and time for a single grid user. GARG et al [14] focused on the scheduling of different applications from a community of users considering a commodity market. However, these studies like others discussed above do not consider the inconsistency of resource; i.e., they assume that the heterogeneity of resources is consistent. Inconsistency refers to the performance differences of all tasks across resources [15]. Motivated by this fact, a new DBC scheduling heuristics used in a commodity market model in which the inconsistency of resource heterogeneity was considered was proposed.

3 Proposed scheduling heuristics

3.1 Grid scheduling

In computational grid environments, to improve the utilization and throughput of the resources and satisfy users’ diverse requirements, tasks should be handled at the local and grid level separately [16]. At the grid level, tasks should be assigned to the resources that meet QoS constraints, and within a resource, local policies should be employed to map received jobs to the processing elements. In this work, an economy-driven scheduling heuristics at the grid level, which considers inconsistency of resource heterogeneity and selects appropriate resources in order to complete as many user jobs as possible within deadline and budget limits, was proposed. The availability and capabilities of the resources vary frequently in grid environments, thus, grid scheduling should be capable of dealing with the dynamic nature of these resources. As such, the heuristics proposed is dynamic, and enables mapping decisions to be done during the execution of a schedule.

3.2 Problem definition

Before introducing the scheduling heuristics, we first define several terms and introduce some notation used in the algorithm. In this work, the newly proposed heuristics is primarily designed for scheduling sequential workflows with each sequential workflow representing a sequence of activities or stages. Each stage is an application task, which is decomposed into a set of independent subtasks. From hereon, task and subtask will be used interchangeably. Some applications in scientific fields conform to a sequential workflow application such as the research of JITHESH et al [17] in which the output of an activity returned from a grid service becomes the input for a subsequent activity. Fig.1 gives an example of a sequential workflow application.

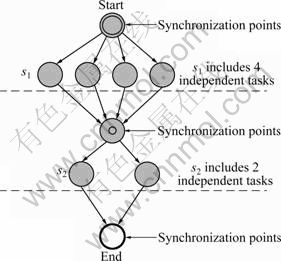
Fig.1 Sequential workflow application

A sequential workflow is represented as (S, (d, b)), where S is composed of a set of application tasks, d is the duration of the workflow, and b represents the budget of S. We define |S| to be the number of stages in workflow S such that s_i represents the i-th stage. Then, S={s_i, 0≤i<|S|}. Each application task is decomposed into a set of subtasks: ||S|| and ||s_i|| indicate the workflow total size and the size of the i-th stage, respectively, such that |s_i| represents the number of subtasks in the i-th stage. Then s_i={s(i,j), 0≤j<|s_i|}, where s(i,j) indicates the j-th subtask of i-th stage. A grid environment consists of a set of resources R such that |R| represents the number of resources in the set R and r_k represents the k-th resource. Then R={r_k, 0≤k<|R|}. In addition, in a dynamic scheduling process, there is a set of subtasks, T, waiting to be mapped. We define |T| to be the number of subtasks, T={t_l, 0≤l<|T|}. The expected execution time T_E(l,k) of t_l on r_k is defined as the time taken by r_k to execute t_l given that r_k has no load when t_l is assigned. The estimated time of each subtask on each computer resource is assumed to be known based on the technique of JANG  et al [18]. The expected completion time T_C(l,k) of t_l on r_k is defined as the wall-clock time at which r_k completes t_l (after having finished any previously assigned tasks). Let the beginning time of t_l be B_l. From the above definitions, T_C(l,k)=B_l+T_E(l,k).

3.3 Conventional DBC scheduling algorithm

In the grid economy framework, the resource brokers use economy-driven deadline and budget constrained scheduling algorithms for allocating resources to application jobs in such a way that the users’ requirements are met [13]. A number of heuristics for DBC scheduling of independent task applications on the grid have been developed. They are: DBC cost optimization algorithm, DBC time optimization algorithm and DBC time-cost optimization algorithm. The description of DBC time optimization algorithm is as follows.

1) For each resource, calculate the next completion time for an assigned task, taking into account of previously assigned tasks;

2) Sort resources by next completion time;

3) Assign one task to the first resource for which the cost per task is less than or equal to the remaining budget per task;

4) Repeat all steps until all tasks are assigned.

The time optimization strategy produces results as early as possible before a deadline and within a budget limit.

The cost optimization algorithm attempts to complete the application as economical as possible within the deadline. The steps are as follows.

1) Sort resources by increasing cost;

2) For each resource in order, assign as many tasks as possible to the resource, without exceeding the deadline.

The description of time-cost optimization algorithm is as follows.

1) Sort resources by next cost per task;

2) Assign one task to the first resource for which the cost and time are less than or equal to the remaining budget and deadline.

The DBC time-cost optimization algorithm attempts to complete the experiment economically and quickly before a deadline and within a budget limit.

The heuristics described above are for independent task scheduling. In order to schedule a sequential workflow, which is composed of some stages, the conventional DBC heuristics is designed based on the above heuristics. The strategy takes three inputs: an application represented as a workflow, a budget that the user is willing to spend for the application, and a deadline in which the results of the application must be returned. The conventional DBC scheduling heuristics is presented as follows.

1) Share the total budget and the total duration among the stages of the workflow in proportion to total subtask size of each stage, ||s_i||;

2) For each stage in the workflow;

3) Estimate maximum expense (maxEE) and maximum duration (maxED);

4) Sort all subtasks in the increasing order of task size;

5) If the stage budgetmaxED;

6) Adopt cost optimization algorithm;

7) Else if the stage budget >maxEE and the stage duration

8) Adopt time optimization algorithm;

9) Else;

10) Adopt time-cost optimization algorithm;

11) Wait for the completion of all l-th subtasks;

12) Estimate the real expense and duration spent in this stage, which is used to adjust the budget and duration of the next stage.

For each stage of the workflow, if the duration is sufficient but the budget is insufficient, the cost optimization strategy is used in which cheaper resources are given precedence over expensive ones. On the other hand, if the budget is sufficient but the duration is insufficient in terms of these comparisons, the time optimization strategy is used in which faster resources are given precedence over slower ones. Finally, in the case that both of them or none of them are sufficient, the time-cost optimization strategy is used in which relatively faster and cheaper resources are given priority.

3.4 Proposed novel DBC scheduling heuristics

The above algorithm does not consider the inconsistency of resource heterogeneity. It assumes that the heterogeneity of resource is consistency. Fig.2 shows the inconsistency of two tasks and four resources. Task 1 and task 2 get higher performance for resource 1. However, on other resources (resource 2, resource 3, and resource 4), the execution time of task 1 increases greatly. On the contrary, the execution time of task 2 for resource 2, resource 3, and resource 4 increases only a little.

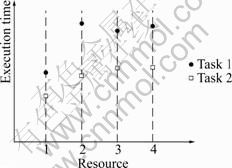
Fig.2 Inconsistency of resource heterogeneity

In order to evaluate the performance difference of the tasks on resources, we introduce the concept of relative cost, which is an approximation of this difference. The relative cost (RC) is calculated by computing the minimum execution time divided by the average execution time of that task for all resources. Thus, the RC value of the l-th task for resources is given as

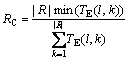                               (1)

When the relative cost is high, the minimum execution time is similar to the average and most of the execution time on all resources are similar. When the relative cost is low, the minimum execution time is very different from the average. If the relative cost for a task is high, then there is a low probability that the task will suffer more than a task that has a low relative cost. So, task 1 is considered to suffer more than task 2 because there is a larger difference between the execution time of the best and the second resources.

Motivated by this fact, we presented a new DBC scheduling heuristics for sequential workflow, which considers time, cost and RC together. According to conventional heuristics, small tasks are given priority in scheduling. So, the new algorithm sorts the tasks according to task sizes at first like conventional algorithm. The tasks are sorted into an increasing ordered list. Then, the task list is partitioned into 10 segments of equal sizes. For each segment, we resort the tasks of every segment in an increasing order of task RC. In general, the new algorithm is described in Fig.3.

Initially, the budget and the total duration are shared among the stages of the workflow in proportion to their total subtask size, and the budget and duration of the first stage are calculated. Then, we estimate the maximum expense (maxEE) and the maximum duration (maxED) of this stage. CPMI indicates the cost per million instructions while MIPS represents million instructions per second. In each stage, all subtasks are sorted in the increasing order of subtask sizes. Then, the subtask list is divided and resorted. After comparing the budget and the duration with the estimated ones, which indicates how much time and budget is required to process all the subtasks in the worst case, one of the three methods is used. If the duration is sufficient but the budget is insufficient, resources are sorted in the increasing order of CPMI. On the other hand, if the budget is sufficient but the duration is insufficient in terms of these comparisons, the heuristics ranks resources in a decreasing order of MIPS. In the case that both of them or none of them are sufficient, resources are sorted in the decreasing order of MIPS/CPMI. Then, according to the order of subtasks and resources, subtasks are assigned to resource in order. If there are remaining subtasks, which are not mapped, the heuristics assigns these tasks to each resource in order and repeats until all tasks are mapped. After completing the task mapping, all the outputs have to wait, since the next stage in the workflow can be initiated after the completion of the current one. On receiving all the outputs, the real expense and duration are calculated, and their differences in the assigned portions are reflected on the budget and duration of the next stage as surpluses or debts. The heuristics runs until all the stages are completed or an interruption occurs due to a budget or deadline violation.

Fig.3 RC-BC heuristics for sequential workflow

4 Building simulations and experimental testing

In order to simulate grid scheduling in grid environment, we used the GridSim toolkit (V.4.2) [19] to evaluate the new RC-DBC scheduling algorithm and compare it with conventional algorithms.

4.1 GridSim toolkit

In a grid environment, it is hard and even impossible to perform scheduler performance evaluation in a repeatable and controllable manner as resources and users are distributed across multiple organizations with their own policies. To overcome this limitation, a Java-based discrete-event grid simulation toolkit called GridSim was developed. The toolkit supports modeling and simulation of heterogeneous grid resources, users, application models, and so on.

GridSim supports entities for simulation of single- and multi-processor heterogeneous resources. It supports entities that simulate networks used for communication among resources. During simulation, GridSim creates a number of multi-threaded entities, each of which runs in parallel in its own thread. The behavior of an entity needs to be simulated within its body() method. GridSim based simulations contain entities for the users, brokers, resources, and grid information service (GIS). The interactions between these entities are illustrated in Fig.4.

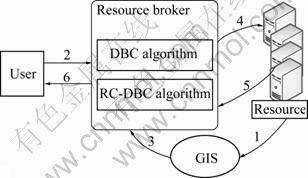
Fig.4 Architecture of interaction of entities

1)The interaction processes of these GridSim entities are as follows.

2)1) GridSim GIS entity gets information of resources;

2)2) The user entity creates a list of applications and sends user requirements to the broker;

2)3) The resource broker trades with the GridSim GIS entity to identify the contact information of the resources, and then interacts with resources to establish their configuration and access cost;

2)4) The scheduling manager selects a scheduling algorithm for mapping tasks to resources depending on the experiments of conventional algorithm and novel algorithm;

6)5) When the task processing completes, the resource returns to the broker’s receptor module;

6)6) Repeat steps 4-5 until all the tasks are processed or the broker exceeds the deadline or budget limits;

7) At the end, the broker returns results back to the user entity.

4.2 Resources and benchmarks

In order to simulate the grid environment, we modeled and simulated a number of resources with different characteristics, configurations, and capabilities. The latest system models were selected, which were released by their manufacturers: Sun Microsystems, SGI, Bull SAS, Intel Corporation, IBM Corporation, and Hewlett-Packard Company. The price of these resources is hypothetical because there is no real data for reference. Table 1 lists the characteristics of the experimental resources.

The processing capability of these resources is modeled after the base value of SPEC CPU (CFP) 2006 [20]. To enable the users to model and express their application processing requirements, we selected eight typical benchmarks and their execution time on the resources from the reference data. A benchmark is a standard of measurement or evaluation. A computer benchmark is typically a computer program that performs a strictly defined set of operations (a workload) and returns some form of result (a metric) describing how the tested computer performs. Here, the metric is execution time. According to the execution time, we calculated the relative costs of these benchmarks. Table 2 presents the execution time and relative costs of these benchmarks. When 436.cactusadm and 444.namd compete in resource 1 at the same time, it is reasonable to assign 436.cactusadm to resource 1. This is because the relative cost of 436.cactusadm is less than that of 444.namd.

4.3 Users and workflow applications

The user essentially interacts with a resource broker that hides the complexities of grid computing. The broker discovers resources that the user can access using information services, maps jobs to resources (scheduling), stages the application and data for processing (deployment), starts job execution, and finally gathers the results. In the experiment, we simulated six users and eight kinds of different workflow applications. Users randomly select eight different workflows. A grid user could have many workflows to be processed. So, users also select these workflows repeatedly. Given that different workflow applications may have different impact on the performance of the scheduling algorithms, here we simulated eight different kinds of workflows. Table 3 lists all kinds of workflow applications in our designed experiment. For example, workflow1 is composed of 3 stages and the application should be finished within 9 000 $ and 2 000 s.

Table 1 Attributes of experimental resources

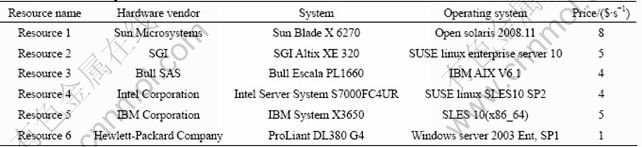
Table 2 Execution time and relative cost of benchmarks

Table 3 Designed workflow applications

4.4 Experimental results and discussion

The performance of the conventional DBC heuristics and the RC-DBC heuristics was analyzed. The main criterion in this experiment is the ratio of successful workflow completion before deadline and within budget. Another criterion is task completion ratio.

Each user randomly selected workflows from those eight workflows shown in Table 3. There were ten experimental settings for the number of workflows, users could randomly select; i.e., 6, 12, 18, etc., as shown in the X-axis of Fig.5 and Fig.6. We repeated every experimental setting 20 times to get the average of workflow completion ratio and task completion ratio.  In all of the experiments, users submit tasks randomly based on a Poisson arrival process. As results of these experiments, Fig.5 presents the comparison of task completion ratios, and Fig.6 shows the results about the workflow completion ratios.

As shown in Fig.5 and Fig.6, the performances of these two heuristics drop when the number of participating workflows increases since the amount of resources cannot support increased demands. When the amount of resources is enough for workflows, i.e., in the case that the number of workflows is six and the ratios of tasks and workflows completion are same, the value is 1.0.

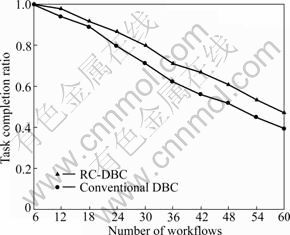
Fig.5 Comparison of task completion ratio

Based on these results, it is clear that the new heuristics outperforms the conventional heuristics. In fact, these workflows are composed of different kinds of tasks, which perform differently on the same resource. In the new heuristics, relative cost is considered when tasks are mapped to resources. The more tasks are completed before deadline and within budget, the more workflows are finished before deadline and within budget.

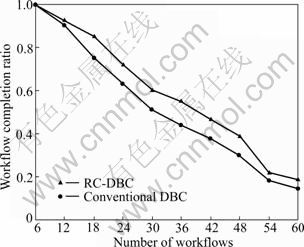
Fig.6 Comparison of workflow completion ratio

5 Conclusions

1) A novel RC-DBC scheduling algorithm that considers the inconsistency of grid heterogeneity is presented. Relative cost is introduced to evaluate the value of inconsistency. A relative cost component is added into the conventional DBC heuristics to form the new RC-DBC heuristics.

2) The GridSim toolkit and the benchmark suits of SPEC are used to test the new scheduling algorithm in a simulated grid environment. The experimental results show that the relative cost guided heuristics outperforms the conventional DBC heuristics in application completion ratio.

References

[1] FOSTER I. Globus toolkit version 4: Software for service- oriented systems [C]// IFIP International Conference on Network and Parallel Computing. Beijing: Springer Berlin, 2005: 2-13.

[2] FOSTER I, KESSELMAN C. The grid: Blueprint for a new computing infrastructure [M]. San Francisco: Morgan Kaufmann Publishers Inc, 1999: 10-16.

[3] FERN?NDEZ-BACA D. Allocating modules to processors in a distributed system [J]. IEEE Transactions on Software Engineering, 1989, 15(11): 1427-1436.

[4] BUYYA R, ABRAMSON D, GIDDY J, STOCKINGER H. Economic models for resource management and scheduling in grid computing [J]. Concurrency and Computation: Practice and Experience, 2002, 14(13): 1507-1542.

[5] PELLICER S, LIU H, PAN Y. Mapping, scheduling, and fault tolerance in grid environments [M]// Engineering the Grid: Status and Perspective. California: American Scientific Publishers, 2006: 370-391.

[6] BRAUN T D, SIEGEL H J, BECK N, BOLONI L, FREUND R F, HENSGEN D, MAHESWARAN M, REUTHER A I, ROBERTSON J P, THEYS M D, YAO B. A comparison of eleven static heuristics for mapping a class of independent tasks onto heterogeneous distributed computing systems [J]. Journal of Parallel and Distributed Computing, 2001, 61(6): 810-837.

[7] KIM J K , SHIVLE S, SIEGEL H J. Dynamic mapping in a heterogeneous environment with tasks having priorities and multiple deadlines [C]// Proceedings of the 17th International Symposium on Parallel and Distributed Processing, Washington D C: IEEE Computer Society, 2003: 98-110.

[8] SHETTY S, PADALA P, FRANK M P. A survey of market-based approaches to distributed computing [R]. Gainesville: Department of Computer and Information Science and Engineering, University of Florida, 2003: 3-7.

[9] VENUGOPAL S, BUYYA R. A deadline and budget constrained scheduling algorithm for science applications on data grids [C]// 6th International Conference on Algorithms and Architectures for Parallel Processing (ICA3PP-2005). Melbourne: Springer, 2005: 60- 72.

[10] FENG Hao-lin, SONG Gang-hua, ZHENG Yao, XIA Jun. A deadline and budget constrained cost-time optimization algorithm for scheduling dependent tasks in grid computing [C]// Second International Workshop on Grid and Coorperative Computing. Shanghai: Springer, 2003: 113-120.

[11] SINGH G, KESSELMAN C, DEELMAN E. A provisioning model and its comparison with best-effort for performance-cost optimization in grids [C]// Proceedings of the 16th International Symposium on High Performance Distributed Computing. California: ACM Press, 2007: 117-126.

[12] WIECZOREK M, PODLIPNIG S, PRODAN R, FAHRINGER T. Bi-criteria scheduling of scientific workflows for the Grid [C]// Cluster Computing and the Grid 2008. Lyon: IEEE Cpmputer Society, 2008: 9-16.

[13] BUYYA R, MURSHED M, ABRAMSON D, VENUGOPAL S. Scheduling parameter sweep applications on global grids: A deadline and budget constrained cost-time optimization algorithm [J]. Software: Practice and Experience, 2005, 35(5): 491-512.

[14] GARG S, BUYYA R, SIEGEL H J. Scheduling parallel applications on utility grids: Time and cost trade-off management [C]// Proceedings of the 32nd Australasian Computer Science Conference (ACSC 2009). Wellington: Australian Computer Society, 2009: 151-159.

[15] ARMSTRONG R. Investigation of effect of different run-time distribution on smart net performance [D]. Monterey: Department of Computer Science, Naval Postgraduate School, 1997: 82-88.

[16] RANGANATHAN K, FOSTER I. Simulation studies of computation and data scheduling algorithms for data grids [J]. Journal of Grid Computing, 2006, 1(1): 53-62.

[17] JITHESH P V, KELLY N, SIMPSON D R. Bioinformatics application integration and management in GeneGrid: experiments and experiences [C]// All Hands Meeting (AHM2004), Nottingham, UK: Jhon Wiley and Sons Ltd, 2004: 91-99.

[18] JANG S, TAYLOR V, WU X, PRAJUGO M, DEEL-MAN E, MEHTA G, VAHI K. Performance prediction-based versus load-based site selection:quantifying the difference [C]// Proceedings of the 18th International Conference on Parallel and Distributed Computing Systems. Las Vegas: ACTA Press, 2005: 101-110.

[19] BUYYA R, MURSHED M. GridSim: A toolkit for the modeling and simulation of distributed resource management and scheduling for Grid computing [J]. Concurrency and Computation: Practice and Experience, 2002, 14(15): 1175-1220.

[20] SPEC. SPEC CPU2000 Results [EB/OL]. [2009-07-30]. http://www. specbench.org/osg/cpu2006/results/cpu2006.html.

(Edited by LIU Hua-sen)

Foundation item: Project(60873107) supported by the National Natural Science Foundation of China

Received date: 2010-03-15; Accepted date: 2010-06-15

Corresponding author: WANG Yong, Associate Professor, PhD; Tel: +86-13808669081; E-mail: yongwang@cug.edu.cn