DOI: 10.11817/j.issn.1672-7207.2016.06.019
基于分集接收的卫星认知通信动态频谱感知策略
肖楠，梁俊，张衡阳，刘玉磊，王轶
(空军工程大学 信息与导航学院，陕西 西安，710077)
摘要：针对基于固定判决门限的频谱感知策略无法适应信道衰落变化导致频谱感知效率下降的问题，结合卫星网络中待检测信号能量较低的特点，提出一种Nakagami-m信道环境下基于分集接收的动态频谱感知策略。该策略利用改进的模糊聚类算法动态获得频谱最佳判决门限，使得判决门限能够根据信道衰落变化自适应调整；在此基础上利用MRC(maximum ratio combining)与EGC(equal grain combining) 2种分集方式增大认知用户的接收信噪比，以减小弱信号环境对能量检测算法频谱检测性能的影响。仿真结果表明：该策略能够有效提高低信噪比环境下的频谱感知性能。
关键词：卫星网络；认知无线电；频谱感知；分集接收；动态判决门限
中图分类号：TN927 文献标志码：A 文章编号：1672-7207(2016)06-1959-08
A dynamic spectrum sensing strategy based on diversity reception for satellite cognitive communication
XIAO Nan, LIANG Jun, ZHANG Hengyang, LIU Yulei, WANG Yi
(School of Information and Navigation, Air Force Engineering University, Xi’an 710077, China)
Abstract: The efficiency of fixed decision threshold based spectrum sensing was deteriorated because of its inadequate adaptability to channel fading variations. A novel dynamic spectrum sensing strategy based on diversity reception in Nakagami-m channel fading was proposed for satellite cognitive communication, which takes the character as low energy of signals to be detected in satellite network into consideration. The optimized spectrum decision threshold adjusted dynamically according to the channel fading state using an advanced fuzzy C-Means clustering algorithm, and a signal receive scheme based on MRC (maximum ratio combining) and EGC (equal grain combining) diversity reception technology was designed to enhance the receiving SNR (signal to noise ratio) in order to mitigate the influence of weak signal environment on spectrum sensing. The results indicate that the performance of spectrum sensing is improved remarkably especially in low SNR environment by the proposed dynamic spectrum sensing strategy.
Key words: satellite network; cognitive radio; spectrum sensing; diversity reception; dynamic decision threshold
认知无线电技术是缓解可用频谱资源紧张与已分配频谱利用率低下之间矛盾的一种有效手段。随着认知无线电技术在地面网络中的深入研究与发展，其在卫星通信网中的应用逐渐得到空间研究者的关注，成为一个新的研究领域与热点[1]。文献[2-4]分析了认知无线电技术在卫星通信网络中的应用场景和关键问题，指出认知无线电技术在卫星领域的应用能够有效提升卫星通信系统效能，更好地引导卫星通信异构网络融合发展和智能化演进。频谱感知机制是认知无线电的关键技术之一。在已有频谱检测方法中，基于能量检测的频谱感知策略具有计算简单、易于实现等优点，被广泛应用于认知无线电频谱感知中。文献[5]指出判决门限的选取是影响能量检测法频谱感知性能的关键因素；文献[6-10]分别分析了不同信道衰落环境下采用等增益合并与选择合并技术提高频谱检测性能的基本方法，但未对检测性能进行详细分析且判决门限的选取是根据虚警概率预先设定的，无法适应信道衰落环境变化；文献[11]提出了一种基于循环统计量的频谱空穴检测方案，通过构造频谱空穴检测的二元假设检验模型，推导了相应的检验统计量，提高了频谱检测性能；文献[12]提出了一种基于加窗粒子群优化的卫星网络的上行链路信道检测门限与功率分配联合优化策略，提高据传输量；文献[13]提出了一种基于判决分析的判决门限选取策略，简化了判决门限选择过程并实现了判决门限的动态调整，但是仿真结果表明该方法在接收信噪比为10 dB时性能已经严重下降。在卫星网络中应用认知无线电技术时，由于信号空间传播损耗大且卫星通信天线的指向性，导致认知用户接收到来自授权用户的信号功率很小，认知用户需要检测强度微弱、类型未知的授权用户电磁信号，这种弱信号环境使得认知用户很难直接对频谱占用状态做出准确判断；另一方面，已有基于能量检测的频谱感知策略中判决门限往往是预先设定且不随环境改变的，而由于信道存在衰落、阴影遮蔽效应，认知用户所接收到的待检测信号强度也在不断变化，传统基于固定门限的频谱感知策略无法根据网络环境变化动态调整判决门限，从而导致频谱检测效率的降低[14]。针对上述问题，本文作者提出了一种基于分集接收的卫星认知通信动态频谱感知策略，该策略将动态门限选取与分集接收技术有机结合起来，从而提高低信噪比以及信道衰落动态变化条件下的频谱感知性能。仿真结果验证了该策略的正确性与有效性。
1 系统模型
参考文献[1]中所描述的基于认知无线电的卫星网络模型。假设地面无线网络为认知网络，静止轨道(geostationary orbit，GEO)卫星通信网为授权网络。地面无线通信终端作为认知用户通过一定的频谱感知策略发现授权用户网络中空闲的频谱资源，从而实现对授权用户网络频谱的“机会式”共享，如图1所示。
上述场景中主要存在2种类型的干扰：卫星信号发射对认知用户接收的干扰(干扰链路1)和认知用户信号发射对卫星地面接收的干扰(干扰链路2)。实际上，由于认知用户接收通常并不对准卫星且GEO卫星轨道高度高达35 786 km，因此，卫星对认知用户信号接收的影响基本可以忽略；而卫星地面用户则有可能处在认知用户的有效通信范围内，因此为了避免认知用户信号发射会对授权用户接收的影响，认知用户需要感知授权用户信道占用状态。
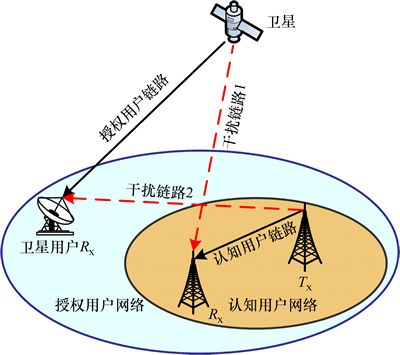
图1 卫星认知通信网络模型
Fig. 1 Network model of satellite cognitive communication
假设认知用户接收到的信号为y(t)，则y(t)包含未知的授权用户信号s(t)与信道噪声n(t)，当采用能量检测法对频谱进行检测时，检测概率Pd (probability of detection)和虚警概率Pf (probability of false alarm)是评价频谱感知算法性能的2个重要指标，根据文献[15]，Pd和Pf分别表示为：
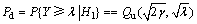(1)
(2)
式中：λ为判决门限；Γ(·,·)为非完全Gamma函数且
，
；Qu(·,·)为广义Marcum Q函数；u为信号的带宽时延积。由式(1)和(2)可知：Pf仅由参数u和λ决定，与信噪比和信道衰落影响等无关，而Pd则由信噪比γ与判决门限λ共同决定。根据文献[16]，在Nakagami-m信道下认知用户接收信号信噪比的概率密度函数为
(3)
式中：
为平均接收信噪比；m为信道衰落深度。当接收信号幅度服从Nakagami-m衰落分布时，γ服从
的Gamma分布，此时频谱检测概率Pd为
(4)
式中：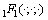
为广义合流超几何函数(p=1，q=1)。对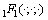进行基于二元变量的扩展，可得：
(5)
相应地频谱漏检概率Pm(probability of miss detection)可以表示为
。针对式(4)中n=∞的问题，为了便于计算，引入截断误差的概念。假设式(4)中n=N时的截断误差为|E|，则根据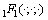函数的单调递减特性可得：
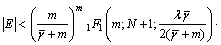
(6)
由式(6)可得Pd满足一定精度要求时的最小N，从而简化式(4)的计算。假设认知用户对频谱准确检测的概率为Prd(probability of right detection)，则Prd可以表示为
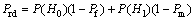(7)
式中：P(H0)与P(H1)分别为频谱空闲与被占用状态出现概率的平均值，且P(H0)+P(H1)=1。
2 动态判决门限
对于认知用户而言，虽然频谱状态是未知的，但是任一频谱却只能有空闲和被占用2种状态，因此，最佳判决门限的选取的实质就是确定λ使得频谱状态的判决结果可信度尽可能高。由于待判决信号究竟属于何种状态具有一定的模糊性，即对于认知用户终端而言信号在未进行判决之前属于2种状态的概率相等，因此，本文引入模糊聚类算法。模糊聚类算法通过设定聚类数目和模糊度常数，并初始化各个聚类中心，每个样本按一定的模糊隶属度隶属于某一聚类中心，然后逐步循环进行迭代，最终完成模糊聚类划分。假设统计周期T内认知用户接收到某一频谱上的信噪比RSN={γl，l=0，1，2，…，N}为N个样本组成的集合；k为预定类别的数目，本文取k=2；mk为每个聚类的中心；
为第i个样本
对于第j个聚类的隶属度函数。用隶属度函数定义的聚类损失函数可以写为
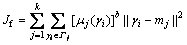(8)
其中：b为可以控制聚类结果模糊程度的常数，b≥1。若b→1，则算法等价于确定性聚类算法；若b→∞，则算法将得到完全模糊的解从而失去分类的意义，因此通常取b=2。在不同隶属度函数下最小化聚类损失函数Jf就可以得到不同的模糊聚类方法，其中最具有代表性的是模糊C均值(fuzzy C-means，FCM)聚类算法。研究表明，对于很难分类的变量，FCM也能够得到比较满意的聚类效果。假设所有样本对各类的隶属度总和为N，即
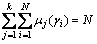(9)
在式(9)条件下求解Jf的最小值，令Jf分别对mk和求偏导数为0，可得必要条件：
(10)
i=1，2，…，N；j=1，2，…，k (11)
初始聚类中心的选取对于FCM算法的聚类效果与收敛速度有较大影响。本文选取的初始聚类中心m1和m2分别可以表示如下：
(12)
式中：N1和N2分别为不同集合中元素的数量。利用式(12)得到的初始聚类中心，通过迭代，最终可以获得最优聚类中心和模糊聚类Γ1和Γ2。假设Γ1表示被占用频谱的聚类，Γ2表示空闲频谱的聚类，此时判决门限λ可以取
(13)
为了评估该判决方法的有效性，本文定义频谱判决效率Pλ：
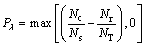(14)
式中：NT为Г1聚类样本总数；Ns为实际信号数；Nc和Nr分别为被正确和错误判决为信号的数量；Nc/Ns为频谱正确检测概率；Nc/Ns为信号的误检概率。可见：当Nr=0且Nc=Ns时，判决效率Pλ取最大值1。
聚类分析属于一种学习或训练方法，其性能与训练样本有较大关系，在实际通信中，认知用户可以通过与认知基站或其他认知用户之间的少量信息交互获得较为准确的训练样本，之后每个认知用户依据该样本独立进行频谱判决门限的设定。
3 基于分集接收的频谱感知策略
分集技术可以充分利用信号和信道的性质，将接收到的多径信号的能量按一定规则合并起来，从而提高接收信号的信噪比，达到抗衰落的目的。常见的分集接收合并技术主要有选择合并(selection combining，SC)、最大比合并(maximum ratio combining，MRC)和等增益合并(equal gain combining，EGC) 3种，其中SC方式虽然易于实现但是由于其并未在同一时刻使用所有可用支路，不能实现接收信号信噪比的最大化，不利于弱信号强度环境下频谱检测，因此，本文重点考虑MRC与EGC 2种分集接收方式。
3.1 基于MRC的频谱检测策略
假设认知用户可以接收来自卫星的L条独立同分布支路的不同信号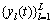
，则接收总信号
，其中hl表示第l条支路信号的加权系数。因此，对于H1假设而言，认知用户的接收信号yM(t)可以表示为
，其中
，
。nl(t)表示第n条支路的噪声信号且nl(t)~N(0，N0)，N0表示噪声功率密度，则每条支路的瞬时信噪比
，即
。认知用户所接收噪声总功率密度
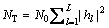，总信噪比
，
可以进一步表示为
(15)
令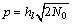
，
，根据Cauchy-Schwarz不等式可知：
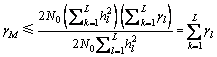(16)
根据Chebychev不等式可知：当
时，取最大值，此时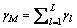
。因此，基于MRC分集接收后合成器输出信号的瞬时信噪比的最大值可以等价为各支路瞬时信噪比之和。此外，由于Nakagami-m信道衰落环境下的接收信噪比服从
的Gamma分布，其中
。由式(4)可知，基于MRC的频谱检测概率
为
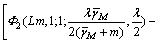
(17)
根据式(6)，此时截断误差函数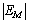
为
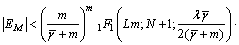
(18)
此时基于MRC的频谱漏检概率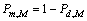
，则频谱准确检测概率
可以表示为
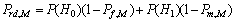(19)
式中：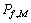
为基于MRC的频谱检测虚警概率，可由式(2)进行计算。
3.2 基于EGC的频谱检测策略
假设认知用户可以同时接收来自L条独立同分布支路的不同信号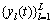，则总接收信号
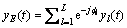，其中
表示第l条支路信号的相位权重。因此，对于H1假设而言，认知用户的接收信号
可以表示为
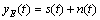，其中
，
表示第n条支路的噪声信号且~N(0，N0)，则总噪声功率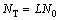
，第l条支路的信噪比。因此，基于EGC的认知用户接收信噪
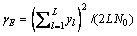。值得注意的是，当各支路信噪比
时，
(20)
对于EGC分集方式而言，当到达接收机的各个支路的信噪比相同时，其性能与MRC是等价的。结合式(1)可知，当采用EGC接收技术且系统中有L条支路时，频谱检测概率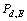
可以通过
的概率密度函数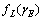
计算如下：
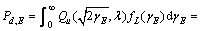
(21)
本文考虑支路数量L=2时认知用户的频谱感知性能。根据文献[18]，当信道为Nakagami-m衰落信道时，由式(3)和式(4)可得接收信号信噪比的概率密度函数
为
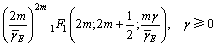(22)
根据Gamma函数的阶乘幂性质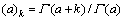
，由式(9)可知：
(23)
结合式(5)，将式(23)代入式(22)得到L=2时频谱检测概率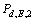
为
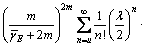
(24)
当m与
确定时，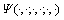
是n的单调递减函数。此时截断误差函数
为
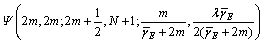(25)
漏检概率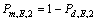
。结合由式(7)可知基于EGC的频谱准确检测概率为
为
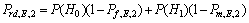(26)
4 仿真结果与分析
为了验证本文所提频谱检测策略的有效性，分别对基于FCM的动态门限选取策略的有效性和在此基础上基于分集接收技术的能量检测机制的频谱感知性能进行仿真分析。
4.1 动态判决门限选取策略有效性分析
假设信号为10个单位幅值的正弦信号的叠加，即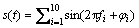
，其中f=[100:100:1 000] Hz，相位φ=[2π/10:2π/10:2π]。信号采样频率fs=5 kHz，采样点数N=5 000。信道采用m=1/2的Nakagami衰落信道模型。选取文献[13]中所采用判别分析法(discriminate analysis，DA)作为对比算法，经过FFT变换后不同信噪比条件下采用不同判决门限策略基于能量检测法的信号判别结果如图2所示。图2中实线表示基于FCM的门限选取结果，虚线表示基于DA的门限选取结果，箭头表示信号实际所处的位置。
由图2可知：当信噪比分别为15 dB和20 dB时，由于信号质量较好，2种方法均能将信号准确识别，判决效率均为100%；当信噪比为10 dB时，基于FCM的门限选取策略仍然可以准确无误地得到信号判决结果，判决效率100%，而DA策略虽然也将信号完全识别出来却增加了7个误判信号，判决效率下降为58.82%；当信噪比为5 dB时，FCM策略能够在错误判决3个信号的基础上准确识别出8个信号，判决效率为52.73%，而DA方法虽然识别出了10个信号但其误判噪声数量却高达51个，判决效率下降为16.39%，由此可见基于FCM的判决门限选取策略的性能优于DA算法的结果。
对于每种信噪比条件下的
计算1 000次，取平均值作为该信噪比下算法的判决效率，并将DA算法作为对比算法，不同算法频谱判决效率的仿真结果如图3所示。由图3可知：2种算法的判决效率均随接收信噪比的增大而增大，但总体而言，基于FCM的判决效率要优于DA策略，当信噪比RSN＞20 dB时，FCM策略的判决效率已经达到100%，而DA策略达到相同的效果要求RSN＞30 dB，反映出FCM判决门限的选取更加有效与合理。
4.2 基于分集接收的频谱检测性能分析
当支路信噪比C1=C2时，MRC与EGC获得相同的改善效果且最大改善增益为3 dB，这与式(20)的理论推导结果相一致。为了更加符合实际信道状况，本文取C1/C2=3 dB，此时MRC与EGC的接收信噪比改善增益分别为2 dB和1.5 dB。图4所示为不同检测策略下频谱漏检概率Pm与虚警概率Pf的仿真结果，其中截断误差E=1×10-6。
由图4可知：当支路信噪比≤30 dB时，本文所提动态频谱检测机制的虚警概率Pf明显小于传统频谱检测策略，且支路信噪比越低，虚警概率性能改善越明显；当支路信噪比≥30 dB时，随着支路信噪比的进一步增加本文所提频谱检测算法与传统频谱检测策略虚警概率性能相近，反映出本文算法更适合于提高低信噪比条件下的频谱检测性能，且采用MRC的性能改善较EGC更为显著。另一方面，随着支路信噪比的增大，本文所提算法的频谱漏检概率Pm略大于传统频谱检测策略的频谱漏检概率，这是由于过高的判决门限会使信号被判决为噪声的概率增大。但总体而言，本文所提出的动态频谱检测策略可以在不显著增大Pm的前提下，在低信噪比环境下有效降低了虚警概率Pf。由于系统内只有2条支路时MRC与EGC的接收信噪比改善增益相差不大，因此在仿真中获得了较为相近的性能，但明显优于不采用分集接收技术时的频谱感知性能。
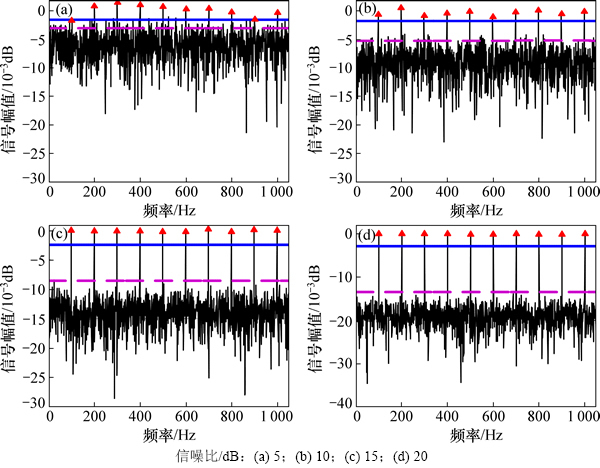
图2 基于FCM的频谱感知策略检测性能
Fig. 2 Performance of spectrum sensing based on FCM
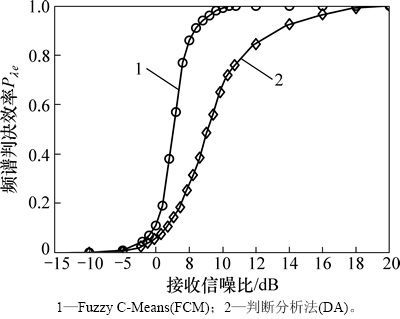
图3 不同门限选取策略时频谱判决效率对比
Fig. 3 Comparison of spectrum judging efficiency of different threshold selecting schemes
图4 不同频谱感知策略下Pm与Pf的仿真结果(L=2，m=1，u=2)
Fig. 4 Curves of Pm and Pf with different spectrum sensing strategies (L=2, m=1, u=2)
图5所示为P(H0)=P(H1)=0.5条件下不同带宽时延积u时Pf的变化曲线。由图5可知：u越小，频谱检测虚警概率Pf越小，但总体性能无较大差异，反映出基于FCM的频谱检测策略对u变化不敏感，具有较好稳定性。
由图4和图5可知：支路信噪比越大，频谱虚警检测概率越小，且高信噪比与低信噪比环境下的频谱检测性能有着显著差异。虽然本文所提动态频谱检测算法在支路信噪比较低时较传统频谱检测机制的频谱感知性能有了一定的提升，但支路信噪比仍然是影响频谱检测性能的关键因素。
图6所示为不同信道环境下不同策略频谱准确检测概率Prd的变化趋势，其中固定判决门限是在m=2，信噪比为20 dB时选定的经验值。随着支路信噪比的增大，Prd也随之增大，当信噪比较低时，固定门限的频谱检测机制性能下降严重，而基于FCM的频谱检测策略性能优异。值得注意的是，当采用FCM策略支路信噪比增大到一定值时Prd反而呈现出下降趋势，这是因为过高的支路信噪比使得判决门限也不断增大，当判决门限增大到一定程度时，虚警概率Pf接近于0，此时漏检概率Pm成为主导Prd变化的主要因素，由图4可知，Pm随着支路信噪比的增大而增大，因此Prd随着支路信噪比的增加逐渐降低，且由于MRC接收信噪比改善增益较大Prd反而下降更快；此时固定门限策略Prd随着支路信噪比的增加而增加直至为1并保持稳定，虽然当支路信噪比＞35 dB时固定门限策略的频谱检测性能优于FCM策略，但是如此之高的支路信噪比不符合本文所考虑的弱信号环境，因此总体来看基于FCM的分集接收频谱感知策略在弱信号环境下取得了较好的频谱判决效果。另一方面，当采用分集接收技术时，无论是在信道较好环境还是信道较差环境下Prd并无显著变化，即使不采用分集接收技术时基于FCM的频谱检测策略也取得了不错的性能，这是由于动态判决门限策略能够根据信道环境的变化做出相应的调整，保证门限的选取能够始终适应当前信道的特点；而对于固定判决门限策略，不同信道衰落环境下频谱感知性能差异较大，这是由于固定判决门限无法根据信道衰落环境的变化进行自适应调整，从而导致频谱检测性能的下降，进一步反映出FCM策略良好的环境适应性。
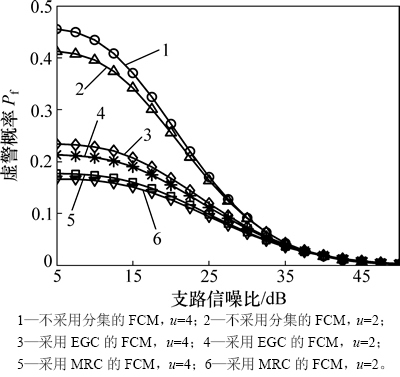
图5 不同频谱感知策略Pf随u变化的仿真结果
Fig. 5 Curves of Pf according to u with different spectrum sensing strategies
图6 不同频谱感知策略下的Prd(L=2，u=5)
Fig. 6 Prd with different spectrum sensing strategies (L=2, u=5)
5 结论
1) 以认知无线电在卫星通信网络中的应用为背景，提出了一种基于分集接收的动态频谱感知策略。该策略以能量检测法为基础，能够根据信道衰落变化动态调整频谱判决门限，克服了传统基于固定判决门限的频谱感知算法环境适应能力差的缺点。
2) 针对卫星网络待检测信号能量较低的问题，提出利用分集技术提高待检测信号的信噪比，减小弱信号环境对频谱感知性能影响。仿真结果验证了该频谱感知策略的合理性与有效性，为卫星认知通信中的频谱感知策略设计提供了思路。
参考文献
[1] SHARMA S K, CHATZINOTAS S, OTTERSTEN B. Cognitive radio techniques for satellite communication systems[C]//2013 IEEE 78th Vehicular Technology Conference. NF: IEEE, 2013: 1-5.
[2] BIGLIERI E. An overview of cognitive radio for satellite communications[C]//2012 IEEE First AESS European Conference on Satellite Telecommunications. Piscataway: IEEE, 2012: 1-3.
[3] HOYHTYA M, KYROLAINEN J, HULKKONEN A, et al. Application of cognitive radio techniques to satellite communication[C]//IEEE International Symposium on Dynamic Spectrum Access Networks. Bellevue, WA, 2012: 540-551.
[4] SHARMA S K, CHATZINOTAS S, OTLERSTEN B. Satellite cognitive communications: interference modeling and techniques selection[C]//Advanced Satellite Multimedia Systems Conference (ASMS) and 12th Signal Processing for Space Communications Workshop (SPSC). Munich, German, 2012: 111-118.
[5] KANDEEPAN S, De NARDIS L, DI BENEDETTO M G, et al. Cognitive satellite terrestrial radios[C]//IEEE Global Telecommunications Conference (Globecom 2010). NJ: IEEE, 2010: 1-6.
[6] HERATH S P, RAJATHVEA N, TELLAM BURA C. Energy detection of unknown signals in fading and diversity reception[J]. IEEE Transactions on Communication, 2011, 59(9): 2443-2453.
[7] FADEL F D, MOHAMED S A, MARVIN K S. On the energy detection of unknown signals over fading channels[J]. IEEE Transactions on Communication, 2007, 55(1): 21-24.
[8] 王悦, 冯春燕, 曾志民, 等. 认知无线电频谱检测机制研究[J]. 吉林大学学报(信息科学版), 2008, 26(3): 230-236.
WANG Yue, FENG Chunyan, ZENG Zhimin, et al. Research on spectrum sensing mechanisms of cognitive radio[J]. Journal of Jilin University (Information Science Edition), 2008, 26(3): 230-236.
[9] 张雯, 杨家玮, 赵伟光. 认知无线电中Nakagami信道下等增益合作检测性能分析[J]. 北京邮电大学学报, 2010, 33(6): 93-97.
ZHANG Wei, YANG Jiawei, ZHAO Weiguang. Analysis on performance of equal gain combination for cooperative spectrum sensing over Nakagami channels in cognitive radio[J]. Journal of Beijing University of Posts and Telecommunications, 2010, 33(6): 93-97.
[10] SHARMA S K, CHATZINOTAS S, OTTERSTEN B. Exploiting polarization for spectrum sensing in cognitive SatComs[C]//International ICST Conference on Cognitive Radio Oriented Wireless Networks and Communications. Istanbul, Turkey, 2012: 36-41.
[11] 陈鹏, 邱乐德, 王宇. 卫星认知无线电检测门限与功率分配联合优化算法[J]. 西安交通大学学报, 2013, 47(6): 31-36.
CHEN Peng, QIU Lede, WANG Yu. Joint optimization algorithm of detection threshold and power allocation for satellite underlay cognitive radio[J]. Journal of Xi’an Jiaotong University, 2013, 47(6): 31-36.
[12] KURT B, WENDY V M. Automatic detection, estimation, and validation of harmonic components in measured power spectra: all-in-one approach[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(3): 1061-1069.
[13] LEE G F, BARBE K, VANMOER W, et al. Cognitive radios: discriminate analysis finds the free space[J]. IEEE Transactions on Communication, 2013, 32(4): 2012-2019.
[14] FENG Yan, JIAO Bingli, SONG Lingyang. Satellite-based spectrum sensing for dynamic spectrum sharing in ground-located CRNs[J]. Wireless Personal Communication, 2011, 57(1): 105-117.
[15] DHARMWANSA P, RAJATHEVAN N, AHMED K. On the distribution of the sum of Nakagami-m random variables[J]. IEEE Transactions on Communication, 2007, 55(7): 1407-1416.
[16] MEKKI S, DANGER J, LMISCOPEIN B, et al. Chi-squared distribution approximation for probabilistic energy equalizer implementation in impulse-radio UWB receiver[C]//IEEE International Conference Communication System. NJ: IEEE, 2008: 1539-1544.
[17] TRADROUS J, SULATAN A, NAFIE M. Admission and power control for spectrum sharing cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2011, 10(6): 1945-1955.
[18] LI Hanqing, GUO Qing, LI Qingzhong. Satellite-based multi-resolution compressive spectrum detection in cognitive radio networks[C]//International Conference on Instrumentation & Measurement, Computer, Communication and Control. Harbin, 2012: 1081-1085.
(编辑 赵俊)
收稿日期：2015-06-10；修回日期：2015-09-03
基金项目(Foundation item)：国家自然科学基金资助项目(61501496)(Project(61501496) supported by the National Natural Science Foundation of China)
通信作者：肖楠，博士，从事空间通信组网技术研究；E-mail：heroamy@163.com
