DOI: 10.11817/j.ysxb.1004.0609.2020-35760

Johnson-Cook本构模型参数估计研究

舒  畅¹ ，程  礼¹，许  煜²

(1. 空军工程大学 航空工程学院，西安 710038；

2. 中国人民解放军93152部队，通化 134000)

摘  要：为研究BT3-1钛合金的力学性能，比较不同算法及试验条件下估计Johnson-Cook本构模型参数的差异，通过材料力学性能试验，获得真实应力-应变曲线，结合几种常见算法估计其本构模型参数，并分析了不同应变率及温度数据处理方式对估计的影响。结果表明：在准静态压缩试验中，BT3-1钛合金的弹性模量、流动应力对应变率敏感性不同；在SHPB试验中，该材料随温度软化效应明显，且伴随着一定的应变率强化现象。名义上某一应变率和温度下的霍普金森压杆试验，实际应变率在名义应变率附近波动，实际温度受到加载应变率及加载温度的共同影响；不同估计算法会造成运算时间、估计结果的差异，用SHPB试验数据估计参数时，若直接采用试验设定的应变率及温度数据，将会造成较大的估计偏差，应考虑加载过程中的温度变化。

关键词：霍普金森压杆试验；Johnson-Cook本构模型；最优化算法；参数估计

文章编号：1004-0609(2020)-05-1073-11　　     中图分类号：O346　　     文献标志码：A

在爆炸、冲击相关领域的研究中，材料处在高应变率和高温环境，发生了较大变形，常采用Johnson-Cook本构模型^[1]描述金属材料的动态变形行为。该模型参数大多由霍普金森压杆试验^[2](Split Hopkindon Pressure Bar，SHPB)确定，该试验能实现最高为1×10⁴ s^-1应变率^[3]加载。在参数估计过程中，有关学者提出了诸多方法^[4-6]，以最优化算法和逐步估计法较为常见。

最优化算法运用数学思想将材料参数估计转化为最优化问题，旨在寻找最优点使得实验数据与预测模型之间的偏差最小^[7]。该方法可以兼顾多组数据间的联系，并且同时确定所有材料参数。最优化算法包含许多具体的算法种类，许多学者也将它们应用于材料的Johnson-Cook本构模型(简称J-C本构模型)参数估计中。例如，张雪强^[8]采用过模拟退火算法、柳爱群等^[9]运用过共轭梯度法、季玉辉^[10]采用过Levenberg- Marquard算法、韩悌信等^[11]运用过遗传算法。2019年，黄赓等^[12]学者还采用了单纯形法对45钢冷滚打成形的J-C本构模型参数进行标定，并结合有限元软件数值模拟，通过控制仿真与实验间滚打力的误差精度来修正参数值。虽然参数估计涉及到的算法众多，但选用不同算法对同组试验数据优化结果是否产生影响，以及对哪些参数估计结果影响较大等问题还有待研究。

逐步估计法则是将本构模型方程中的硬化效应、应变率效应及温升效应进行解耦，然后固定其中任意两种效应，估算出另外一种效应的参数，并逐步估计出所有参数。刘二亮等^[13]在研究Inconel625高温合金热变形行为时就采用此方法确定了该材料的J-C本构模型参数，但拟合结果并不理想，平均误差达10%，因此通过构造幂函数多项式改进了该模型的应变率系数。类似地，胡道春等^[14]研究C5191-H磷青铜高速冲裁本构关系时也发现用逐步估计法得到的拟合曲线不够准确，并修正了J-C模型的指数硬化项。分析该方法产生较大误差的原因，除了材料因素外，该方法本身也存在局限性。一方面，逐步估计过程采用的是试验设定的多组恒定应变率数据以及恒定温度值。实际上，SHPB试验没有实现严格的等应变率加载，也不是严格的等温试验^[15]。金属材料在高应变率时发生绝热变形导致温度升高，故难以保证试验温度恒定。另一方面，解耦的办法忽略了每条试验曲线间的有机联系。因此，近年来李云飞等^[16]研究钛合金动态本构关系时采用逐步估计法得到J-C本构模型参数后，仅将其作为优化函数的初始值并继续进行局部搜索优化，以得到更高精度的解。

为比较不同算法估计参数的差异，探究不同应变率、温度数据处理方式对估计结果的影响，本文在BT3-1钛合金材料的力学性能试验的基础上，结合多种算法对该材料J-C本构模型进行参数估计，分析了试验过程中应变率和温度变化情况，研究了试验条件的处理方式对估计准确性的影响规律，为钛合金系列材料J-C本构模型参数估计提供借鉴。

1  J-C本构模型参数定性分析

Johnson-Cook本构模型一般用于描述高应变率和高温环境下材料发生大变形时的强度极限，目前已被大多数有限元软件所采纳，并广泛应用于冲击动力学领域，其表达式^[17]为：

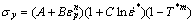             (1)

式中：A、B、n、C和m为材料模型参数，通过试验确定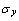；为流动应力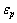；为等效应变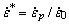；为无量纲化等效塑性应变率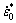；为参考应变率，常取为1 s^-1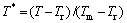；为无量纲化温度；T为试验温度；T_r为参考温度，一般取为室温；T _m为材料熔点温度。式(1)中，等号右边三项分别反映了等效塑性应变、应变率和温度对流动应力的影响，即该模型考虑了材料的加工硬化效应、应变率效应和温度软化效应^[18]。

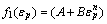为应变硬化函数，反映了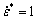、T=0时材料流动应力随应变的变化。参数A、B、n分别表示在参考应变率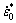和参考温度T_r下的初始屈服应力、硬化模量和硬化指数^[19]。从数学上看，该函数由幂函数和常函数叠加而成。当幂函数指数0＜n＜1时，其第一象限函数的导数值逐渐减小。有关文献实验数据表明^[20],钛合金材料流动应力随应变的增大，上升幅度趋于平缓。因此，当应变率和温度效应影响较小时，钛合金材料硬化指数n取值范围应在(0,1)区间内。

为应变率效应函数，该函数由自然对数函数和常数项叠加而成。由于自然对数函数为增函数，若应变率系数C为正值，则材料具有应变率强化效应，如钢、铜等；若C为负值，材料具有应变率软化效应，如铝锂合金^[21]。

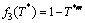为温度效应函数，该函数由幂函数和常数项叠加而成。当幂函数指数为正值，此函数为减函数。大多数金属材料具有温度软化效应，此时温度系数m应为正值。若软化效应随温度逐渐增强，则温度系数m＞1；若软化效应随温度逐渐减弱，则温度系数0＜m＜1。

2  BT3-1钛合金力学性能试验

材料的力学性能试验用于测定材料在一定环境条件下受力或能量作用时所表现出的性能，可分为静力试验和动力试验两大类。本文针对BT3-1钛合金材料进行了准静态压缩试验以及SHPB试验。

2.1  BT3-1钛合金材料

BT3-1钛合金主要用来制造发动机压气机盘、叶片、环和紧固件等能在高温环境下长时间工作的零件，还可作为中强合金制造飞机承力构件及不同用途的紧固件。试验采用的BT3-1钛合金材料从航空发动机一级风扇叶片的榫头部位切取，属于力学各项同性材料，参考了GB/T 7314—2005金属材料室温压缩试验标准设计试样。材料的化学成分如表1所示，其显微组织为等轴组织，由初生α+β相组成，初生α含量约为50%。

表1  BT3-1钛合金化学成分

Table 1  Chemical composition of BT3-1 titanium alloy (mass fraction, %)

2.2  准静态压缩试验

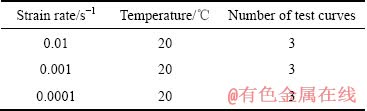
在MTS材料试验机上进行准静态压缩试验，试验方案如表2所示。

表2  准静态压缩试验方案

Table 2  Quasi-static compression test program

将每种应变率下的3组试验结果作平均处理，并得到不同应变率下材料真实应力-应变曲线，如图1所示。

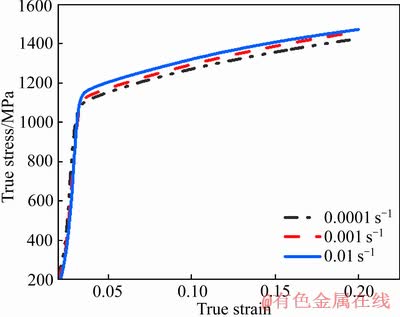
图1  准静态压缩试验的真应力-真应变曲线

Fig. 1  True stress-true strain curves for quasi-static compression experiment

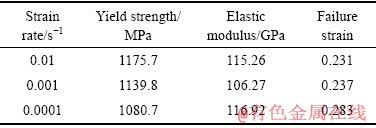
由图1可知，该材料的真实应力随着应变的增加而增大，产生了“加工硬化”现象。这是由于金属变形程度增加时，材料内部晶粒发生畸变和破碎，位错密度增加，从而阻碍了内部晶体滑移，增大了金属塑性变形抗力。比较图1中试验曲线可见，3种应变率条件下曲线的弹性段大致重合，但塑性段的流动应力、屈服强度随应变率的提高而增大。这表明BT3-1钛合金材料的弹性模量受应变率影响小，但流动应力和静态屈服强度表现出应变率强化效应。表3所示为3种应变率下的屈服强度、弹性模量及失效应变，取平均值112.81 GPa作为该材料的弹性模量。

表3  准静态压缩试验结果

Table 3  Quasi-static compression test results

2.3  分离式霍普金森压杆试验

SHPB试验技术的应用最早可追溯到1949年^[22]，如今广泛运用于测量材料在一维应力、高应变率条件下的动态力学性能^[23]。

图2所示为本试验装置原理图，一般由入射杆、透射杆、撞击杆、支架和数据采集系统等组成。试验时，将圆柱形试样放置于入射杆和透射杆之间，撞击杆在高压气体的驱动下，以一定的速度冲击入射杆端面产生弹性波。当弹性波传播到试样和入射杆的端面时，一部分反射回入射杆，而另一部分则透射入试样，引起试件高速塑性变形。部分透射波继续传入透射杆并最终被能量吸收装置所吸收。根据入射杆和透射杆上应变片所采集的数据以及一维弹性波理论，可求出试样应变速率、应变和应力数据^[24]。

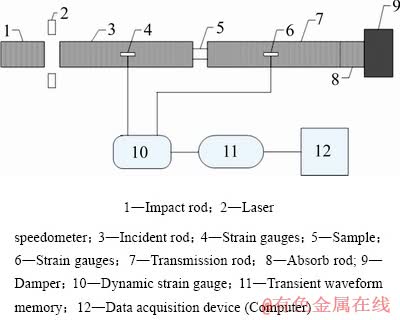
图2  SHPB设备示意图

Fig. 2  SHPB equipment schematic

本文SHPB试验选用直径4 mm，高4 mm的圆柱形试样，试验方案如表4所示。

表4  SHPB试验方案

Table 4  SHPB experimental program

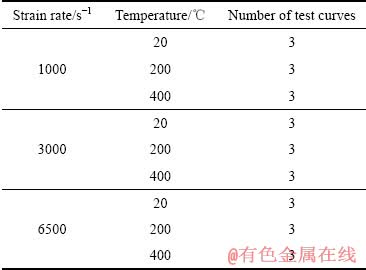
由表4可见，加载应变率和温度的组合将试验条件共分为9种，每种条件下进行3次平行试验。取3次平行试验的平均值作为该试验条件下的试验结果，并转换成材料的真实应力-应变数据，得到如图3，图4的材料性能曲线。可见，SHPB试验因波导杆弯曲效应^[25]，曲线相比于准静态试验曲线存在明显的振荡。

图3所示为BT3-1钛合金在同一应变率、不同温度条件下平均真实应力-应变曲线。由图3可见，在1000、3000和6500 s^-1应变率条件下，温度的升高均引起材料的流动应力和动态屈服强度变小；动态试验中，该材料弹性模量受到温度影响，并且影响程度随着应变率的提高而增大。材料进入塑性变形阶段后，各条曲线的应变硬化模量大致相同，但流动应力随应变增加的程度明显弱于准静态试验曲线。

图3  各应变率下不同温度的真实应力-应变曲线

Fig. 3  True stress-strain curves at different temperatures and various strain rates

图4所示为BT3-1钛合金在同一温度、不同应变率条件下平均真实应力-应变曲线。由图4可见，20 ℃、200 ℃和400 ℃条件下，随着加载应变率的升高，该材料流动应力和动态屈服强度存在增大的趋势， 且图4(a)中各条曲线塑性段的振荡程度略微高于图4(b)和(c)中相应曲线的振荡程度，即低温动态试验中测得的材料流动应力波动较大。

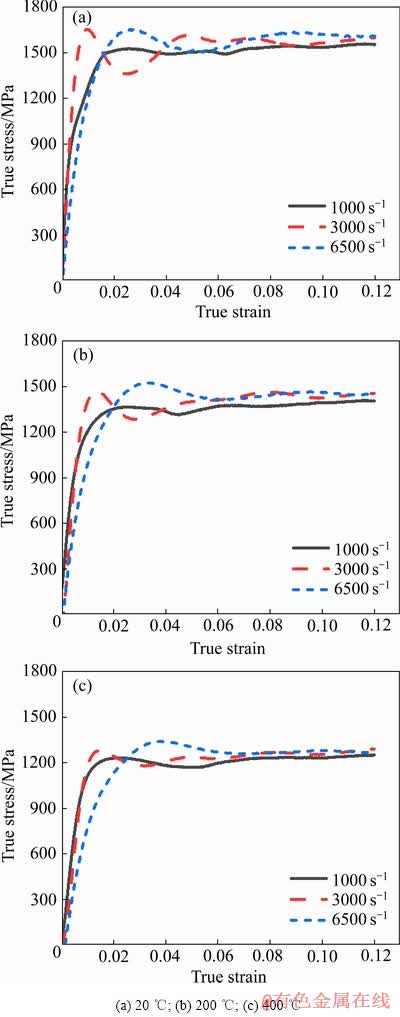
图4  各温度下不同应变率的真实应力-应变曲线

Fig. 4  True stress-strain curves at different strain rates and various temperatures

为了验证SHPB试验并非严格等应变率加载的问题，将试验的应变率响应曲线绘制如图5所示。

由图5可见，真实应变率并非恒定值，且都与名义应变率有一定的偏差。总体而言，应变率响应曲线在名义应变率附近的某一水平上下波动，并且随着应变的增加，存在着降低的趋势，在低应变率条件下表现得尤为明显。此外，应变率响应曲线随温度变化的差异不明显。例如，图5(a)中，名义应变率为1000 s^-1时，400 ℃真实应变率最高而200 ℃真实应变率最低；图5(c)中，名义应变率为6500 s^-1时，20 ℃真实应变率最高而200 ℃真实应变率最低。

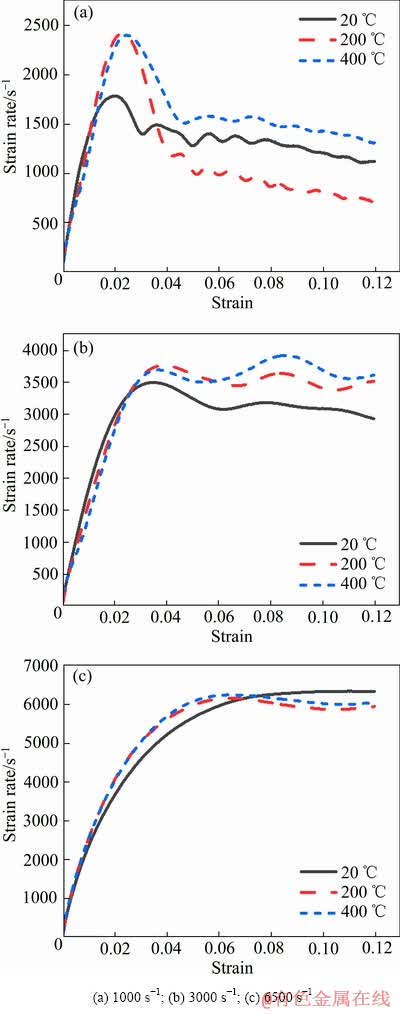
图5  应变率响应曲线

Fig. 5  Strain rate response curves at different nominal strain rates

3  试验数据处理与分析

准静态压缩试验得到了BT3-1钛合金的弹性模量，可用其拟合材料应力-应变曲线的弹性段；SHPB试验得到了材料在高应变率、高温条件下的真应力-真应变曲线，以及应变率响应曲线，但动态试验曲线存在振荡，需要进行平滑处理；此外，处理温度数据时，还要考虑高应变率下材料塑性变形导致的绝热温升现象。

为了得到能准确反映材料的应力-应变关系的曲线，常将弹性变形部分和塑性流动部分分别进行拟合处理^[8]。即材料曲线弹性段用准静态试验数据拟合，而不用动态试验数据^[9]，塑性段则用SHPB试验数据拟合。由此得到了完整的真应力-真应变曲线。

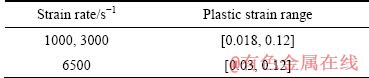
应变率数据处理过程中，由于应变率响应曲线含有上升阶段和平稳阶段，而材料主要在曲线平稳阶段发生塑性变形，因此仅需消除该阶段的曲线振荡。本文截取了表5所示区间段的应变率响应曲线作线性拟合。

表5 塑性段数据处理

Table 5  Data processing in plastic section

温度数据处理过程中，由于高应变率加载时间短，试样内部塑性变形产生的热能无法短时消散，一般采用下式^[26]计算绝热温升：

                          (2)

式中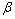：为塑性功-热转换系数，通常取0.9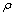；为材料密度；c_p为材料定压比热容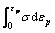；为塑性变形

过程中流变应力所做功，可以通过真实应力-应变曲线中塑性段与坐标轴围成的面积求得。对表5所示塑性区间段计算温升后，得到试验温升如图6和7所示。

由图6可见，在相同温度条件下、不同应变率试验过程中，加载应变率越高，试验过程中温升越大。由式(2)可见，由于应变率强化效应，在高温试验时材料的材料真实应力-应变曲线中的塑性段与坐标轴所围成的面积越大，导致温升幅度增大。

由图7可见，在相同应变率条件下、不同温度试验过程中，加载温度越高，试验过程中温升越小。由式(2)可见，由于温度软化效应，在高温试验时材料的材料真实应力-应变曲线中的塑性段与坐标轴所围成的面积越小，材料的比热容也随温度的升高而增大，上述两者的变化导致温升幅度降低。

图6  3组温度条件下的绝热温升

Fig. 6  Adiabatic temperature rise under three groups of temperature conditions

图7  3组应变率条件下的绝热温升

Fig. 7  Adiabatic temperature rise under three groups of strain rate conditions

4  不同算法参数估计对比分析

本构模型仅描述材料在塑性阶段的力学行为，因此，应选取各状态下材料真实应力-应变曲线中屈服点与失效点之间的数据拟合模型中的参量^[27]。本文采用表5所示的区间段的真应力-真应变曲线数据以及处理后的应变率和温升数据，借助Matlab和First Optimization软件，采用多种算法对J-C本构模型进行参数估计。

用Matlab估计本构模型参数时，采用“最小二乘法”思想，即通过多次迭代，使得拟合数据与试验数据的残差平方和最小，此时的估计值即为最优值。具体而言，需构建如下优化目标函数：

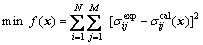            (3)

式中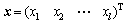：为材料本构模型待定参数；N为用于估算参数的材料试验曲线数目；M为每条试验曲线上用于参数估算的数据点数目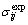；为第i条曲线上第j个数据点的试验应力值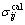；为第i条曲线上第j个数据点的计算应力值。上述目标函数是为了寻求最优参数值使得计算应力-应变曲线与试验应力-应变曲线数据间的残差平方和达到最小值。

本文分别采取了Fminunc函数、Lsqnonlin函数、Lsqcurvefit函数对试验曲线进行最小二乘拟合，每种函数又采用了两种优化算法，估计方案如表6所示，估计结果如表7所示，估计用时如图8所示。

表6  选取的函数和算法

Table 6  Selected functions and algorithms

表7  最小二乘拟合法的参数估计结果

Table 7  Parameter estimation results of least squares fitting method

由表7可见，同种函数对应不同算法的估计结果不产生差异，且选用Lsqnonlin函数和Lsqcurvefit函数估计，能得到相同结果。第1、2组估计值与试验值的残差平方和为8693，其余组估计值与试验值的残差平方和为2619，表明在估计精度方面，Lsqnonlin函数和Lsqcurvefit函数优于Fminunc函数。从图8可见，Lsqcurvefit函数运算效率最高，且其中Levenberg- marquardt算法比Trust-region-reflective算法效率更高。

用First Optimization软件估计本构模型参数时，选用遗传算法(Genetic algorithm, G)、模拟退火法(Simulated annealing algorithm, SA)、粒子群法(Particle swarm optimization algorithm, PSO)、共轭梯度法(Conjugate gradient algorithm, CG)进行参数估计，运算参数保持默认设置，具体结果如表8所示。

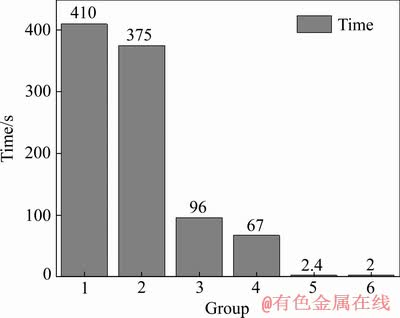
图8  各组估计所用时间

Fig. 8  Time spent on estimation of each group

表8  其余算法参数估计结果

Table 8  Parameter estimation results of other algorithm

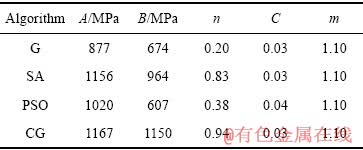
由表8可见，各算法对参数C和m的估计值较为接近，对初始屈服应力A、硬化模量B以及硬化指数n的估计偏差较大。将估计用时及估计精度绘图如图9和10所示。由图9和10可知，共轭梯度法虽然最为费时，但其拟合精度最高；遗传算法和粒子群算法运算效率较高，但估计精度不高；模拟退火算法估计能在较短的时间内获得较高精度。

综上可得，不同算法对J-C本构模型参数估计结果存在差异。此次估计中，选用lsqcurvefit函数的L-M算法得到了最高的估计精度和运算效率，故可考虑在类似的J-C模型参数估计问题上优先采用该算法。

5  应变率及温度数据处理方式对估计结果的影响

由SHPB试验情况可知，即使控制条件为恒应变率、恒温加载，加载过程中仍然存在着应变率和温度变化。因此，要准确地估计参数就应采用试验过程中变化的应变率和温度数据而非恒定数据，但多数文献在估计参数时仅考虑试验过程中的温升而忽略了应变率变化，部分文献中的逐步估计法则将两者都视为定值进行参数估计。

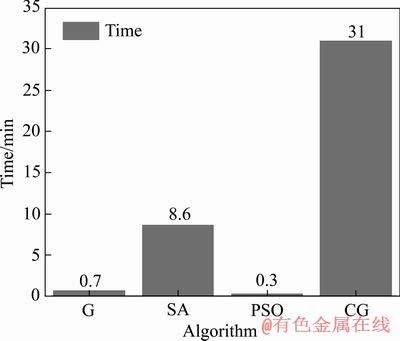
图9  各算法估计所用时间

Fig. 9  Time spent on estimation of each algorithm

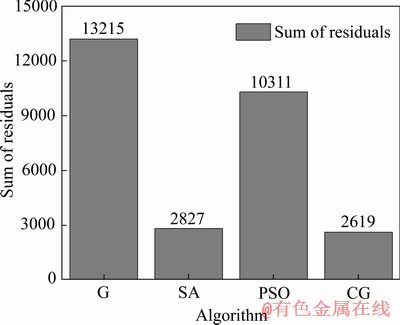
图10  各算法估计精度

Fig. 10  Estimated accuracy of each algorithm

为了分析不同应变率及温度数据处理方式对估计造成的影响，将同时考虑两者变化的参数估计结果作为准确值，考虑其中一者变化或视两者恒定的估计结果作为估计值，通过准确值与估计值的比较，得到相应结论。

根据上述方法及试验结果反映出的应变率和温升变化规律，以应变率3000 s^-1、温度200 ℃作为平均值，制定了表9所示几组不同的应变率和温度线性变化方案。每组数据可视为试验过程中试件发生的真实应变率和温度变化情况。第1、2、3组数据反映了3组试验中试件应变率下降幅度的差异，第2、4、5组数据反映了3组试验中试件温度上升幅度的差异。根据表9及上节参数估计结果，反求得5组真实应力-应变曲线。基于该曲线，用L-M算法进行参数估计，得到估计结果。

当参数估计时，若同时不考虑应变率及温度变化，即采用名义应变率3000 s^-1、名义温度200 ℃参与曲线拟合，得到参数估计值与准确值偏差情况如图11所示。由图11可见，该处理方式下估计参数A偏大，B、n、C、m偏小，且对C的估计偏差最大，对m的估计偏差最小；对比各组参数估计值，应变率变化幅度对各参数估计偏差的影响程度小，而温度上升幅度对各参数估计偏差影响较大，且温升幅度越高，估计偏差越大。

表9  几组不同的应变率和温度变化幅度方案

Table 9  Several different strain rate and temperature change program

图11  视应变率和温度恒定的参数估计偏差

Fig. 11  Parameter estimation without considering change of strain rate and temperature

当参数估计时，若视加载过程中应变率恒定而温度变化，即采用应变率3000 s^-1的恒定值、温度如表9所示的线性变化值参与曲线拟合，得参数估计偏差情况如图12所示。总体而言，该处理方式下估计的各参数值都与准确值偏差较小。由图12(a)可见，应变率变化幅度对估计偏差影响显著，其变幅越大，会导致A的估计值越大，B、n、C估计值越小，m估计值几乎不变；由图12(b)可见，温升幅度大小对各参数估计结果几乎没有影响。

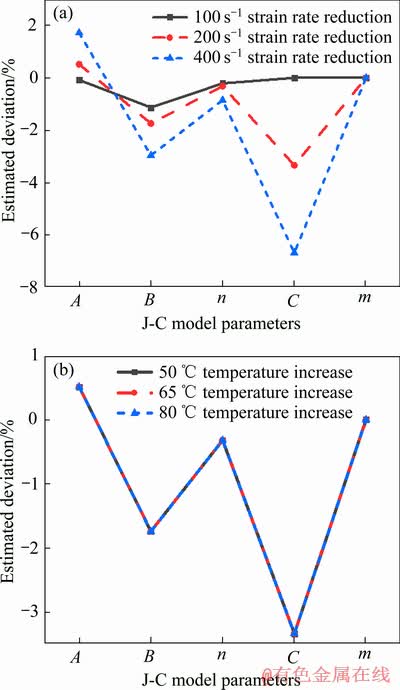
图12  视应变率恒定的参数估计偏差

Fig. 12  Parameter estimation without considering change of strain rate

当参数估计时，若视加载过程中温度恒定而应变率变化，即采用温度200⁰C的恒定值、应变率如表9所示的变化值参与曲线拟合，得到参数估计偏差情况如图13所示。该处理方式下B、n、m估计值比准确值偏小，且C估计偏差很大。由图13(a)可见，试验过程中应变率变化对n估计值影响较小，对C估计值影响较大，且应变率变化越大，A、B的估计值越小；由图13(b)可见，试验过程中温升幅度越大，A的估计值越大，B、n、C估计值越小，m估计值受温度变幅影响较小。

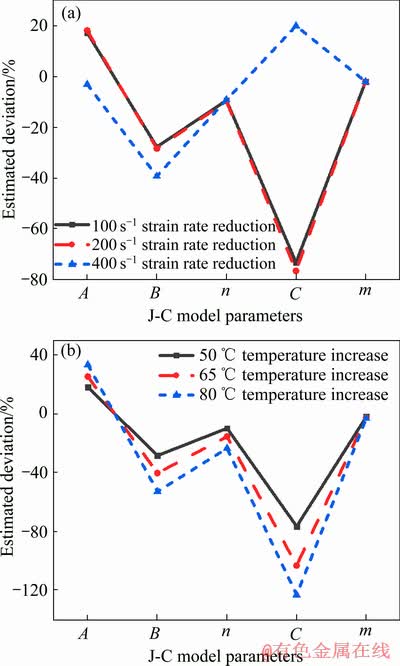
图13  视温度恒定的参数估计偏差

Fig. 13  Parameter estimation without considering change of temperature

综上所述，在估计钛合金材料J-C本构模型参数时，若采用名义应变率，即视SHPB试验过程中的应变率恒定，能够得到与准确值相近的参数估计结果；一旦忽略温度变化，估计值就会离准确值相差甚远，且大部分参数的估计偏差会随两者变化幅度增加而增大。因此，在进行参数估计时，参与拟合的应变率数据可以为名义应变率或真实应变率，温度数据必须考虑加载过程中的绝热温升，估计才能更加准确。

6  结论

1) BT3-1钛合金的准静态压缩试验表明，该材料的弹性模量受应变率影响小，但流动应力和静态屈服强度随应变率的提高而增大。

2) SHPB试验表明，BT3-1钛合金材料随温度软化效应明显，且伴随着一定的应变率强化现象。名义上某一应变率和温度条件下的试验，其实际应变率及温度都存在变化，实际应变率在试验设定的名义应变率上下波动，且有一定的降低趋势，实际温度升幅随名义应变率增加而增大，随名义温度升高而减小，受到两者的共同作用。

3) 采用不同算法估计材料J-C本构模型参数时，运算时间、估计结果都可能产生较大差异。并且，估计值的差异多表现在初始屈服应力A、硬化模量B以及硬化指数n这三个参数上。

4) 钛合金材料J-C本构模型参数估计过程中，采用SHPB试验设定的名义恒定应变率值参与拟合，各参数估计值与准确值偏离较小；采用试验设定的名义恒定温度值，会对估计结果造成较大偏差。因此，在估计参数时不能忽略试验加载过程中的绝热温升。

REFERENCES

[1] JOHNSON G R, COOK W H. Constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[J]. Engineering Fracture Mechanics, 1983, 21: 541-548..

[2] 卢芳云. 霍普金森杆实验技术[M]. 北京: 科学出版社, 2013.

LU Fang-yun. Hopkinson Bar Techniques[M]. Beijing: China Science Publishing & Media Ltd, 2013.

[3] 汤铁钢, 刘仓理. 高应变率拉伸加载下无氧铜的本构模型[J]. 爆炸与冲击, 2013, 33(6): 581-586.

TANG Tie-gang, LIU Cang-li. Constitutive model of OFHC copper under high strain rate tensile loading[J]. Explosion and Shock Waves, 2013, 33(6): 581-586.

[4] SENSENY P E, FOSSUM A F. On testing requirements for viscoplastic constitutive parameter estimation[J]. Journal of Engineering Materials and Technology, 1995, 117(2): 151-156.

[5] FOSSUM A F. Parameter estimation for an internal variable model using nonlinear optimization and analytical/numerical response sensitivities[J]. Transactions of the ASME Journal of Engineering Materials and Technology, 1997, 119(4): 337-345.

[6] BRUHNS O T, ANDING D K. On the simultaneous estimation of model parameters used in constitutive laws for inelastic material behaviour[J]. International Journal of Plasticity, 1999, 15(12): 1311-1340.

[7] MOHRMANN R. Automated identification and calculation of the parameters of non-linear material models[M]// IUTAM Symposium on Field Analyses for Determination of Material Parameters—Experimental and Numerical Aspects. Netherlands: Kluwer Academic Publishers, 2003.

[8] 张雪强. 钛合金叶片外物损伤试验与数值模拟研究[D]. 南京: 南京航空航天大学, 2013.

ZHANG Xue-qiang. Research on experimental and numerical simulation of foreign object damage to titanium alloy blades [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013.

[9] 柳爱群, 黄西成. 高应变率变形的Johnson-Cook动态本构模型参数识别方法[J]. 应用数学和力学, 2014, 35(2): 219-225.

LIU Ai-qun, HUANG Xi-cheng. Johnson-Cook dynamic constitutive model parameter identification method high strain rate deformation[J]. Applied Mathematics and Mechanics, 2014, 35(2): 219-225.

[10] 季玉辉. 基于Johnson-Cook模型的硬物损伤数值模拟研究[D]. 南京: 南京航空航天大学, 2009.

JI Yu-hui. Numerical simulation of hard-body foreign object damage based on Johnson-Cook model[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.

[11] 韩悌信, 曾祥国, 盛鹰. 钛合金动态本构关系的研究及应用[J]. 钛工业进展, 2016, 33(4): 17-21.

HANG Ti-xin, ZENG Xiang-guo, SHENG Ying. Study and application of dynamic constitutive relation for titanium alloy[J]. Titanium Industry Progress, 2016, 33(4): 17-21.

[12] 黄 赓, 李 言, 李 龙, 杨明顺, 李嘉伟, 陈 鑫, 崔莅沐. 45钢冷滚打成形Johnson-Cook本构模型参数标定及修正方法[J]. 西安理工大学学报, 2019, 35(2): 179-185.

HUANG Geng, LI Yan, LI Long, YANG Ming-shun, LI Jia-wei, CHEN Xin, CUI Li-mu. Parameter calibration and correction of Johnson-Cook constitutive model for 45 steel cold roll-beating[J]. Journal of Xi’an University of Technology, 2019, 35(2): 179-185.

[13] 刘二亮, 邢宏伟, 王明明, 徐志超, 赵 娜. Inconel625高温合金J-C本构建模[J]. 中国有色金属学报, 2018, 28(4): 732-741.

LIU Er-liang, XING Hong-wei, WANG Ming-ming, XU Zhi-chao, ZHAO Na. J-C constitutive modeling of high temperature alloys Inconel625[J]. The Chinese Journal of Nonferrous Metals, 2018, 28(4): 732-741.

[14] 胡道春, 王 蕾, 王红军. 基于修正Johnson-Cook模型的C5191-H磷青铜高速冲裁本构关系[J]. 塑性工程学报, 2019, 26(4): 234-240.

HU Dao-chun, WANG Lei, WANG Hong-jun. Constitutive relation in high-speed blanking of C5191-H phosphor bronze based on modified Johnson-Cook model[J]. Journal of Plasticity Engineering, 2019, 26(4): 234-240.

[15] 胡绪腾. 外物损伤及其对钛合金叶片高循环疲劳强度的影响[D]. 南京: 南京航空航天大学, 2009.

HU Xu-teng. Foreign object damage and its effect on high cycle fatigue strength of titanium alloy engine blades[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.

[16] 李云飞, 曾祥国, 廖 异. 基于修正Johnson-Cook模型的钛合金热黏塑性动态本构关系及有限元模拟[J].中国有色金属学报, 2017, 27(7): 1419-1425.

LI Yun-fei, ZENG Xiang-guo, LIAO Yi. Thermal-viscoplastic constitutive relation of Ti-6Al-4V alloy and numerical simulation by modified Johnson-Cook model[J]. The Chinese Journal of Nonferrous Metals, 2017, 27(7): 1419-1425.

[17] 杨增宇, 陈华燕, 赵 黎, 曾祥国. Ti-6Al-4V合金动态本构模型参数敏感性及其优化[J]. 钛工业进展, 2017, 34(5): 17-22.

YANG Zeng-yu, CHEN Hua-yan, ZHAO Li, ZENG Xiang-guo. Parameter sensitivity and optimization for dynamic constitutive relationship of Ti-6Al-4V alloy[J]. Titanium Industry Progress, 2017, 34(5): 17-22.

[18] 朱志武, 宁建国. Johnson-Cook冲击动态本构模型研究[C]//全国塑性力学会议论文集. 北京：中国力学学会, 2011: 78-83.

ZHU Zhi-wu, NING Jian-guo. Research on Johnson-Cook impact dynamic constitutive model[C]//Proceedings of National Conference on Plastic Mechanics. Beijing: Chinese Society of Theoretical and Applied Mechanics, 2011: 78-83.

[19] 范亚夫, 段祝平. Johnson-Cook材料模型参数的实验测定[J]. 力学与实践, 2003, 25(5): 40-43.

FAN Ya-fu,DUAN Zhu-ping. Experimental determination of Johnson-Cook material model parameters[J]. Mechanics in Engineering, 2003, 25(5): 40-43.

[20] 杨 扬, 曾 毅, 汪冰峰. 基于Johnson-Cook模型的TC16钛合金动态本构关系[J]. 中国有色金属学报, 2008, 18(3): 505-510.

YANG Yang, ZENG Yi, WANG Bing-feng. Dynamic constitutive relationship of TC16 titanium alloy based on Johnson-Cook model[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(3): 505-510.

[21] 李建光, 施 琪, 曹结东. Johnson-Cook本构方程的参数标定[J]. 兰州理工大学学报, 2012, 38(2): 164-167.

LI Jian-guang, SHI Qi, CAO Jie-dong. Parameters calibration for Johnson-Cook constitutive equation[J]. Journal of Lanzhou University of Technology, 2012, 38(2) : 164-167.

[22] KOLSKY H. An investigation of the mechanical properties of materials at very high rates of loading[J]. Proceedings of the Physical Society. Section B, 1949, 62(11): 676-700.

[23] NEMAT-NASSER S, ISAACS J B, STARRETT J E. Hopkinson techniques for dynamic recovery experiments[J]. Proceedings: Mathematical and Physical Sciences, 1991, 435(1894): 371-391.

[24] 张长清, 谢兰生, 陈明和. 高应变率下TC4-DT钛合金的动态力学性能及塑性本构关系[J]. 中国有色金属学报, 2015, 25(2): 323-329.

ZHANG Chang-qing, XIE Lan-sheng, CHEN Ming-he. Dynamic mechanical property and plastic constitutive relation of TC4-DT Ti alloy under high strain rate[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(2): 323-329.

[25] 叶仁传, 田阿利, 沈超明. 霍普金森压杆实验波形振荡问题的影响与解决方法[J]. 科学技术与工程, 2014, 14(1): 1-4.

YE Ren-chuan, TIAN A-li, SHEN Chao-ming, The influence and solution of the waveform oscillation problem of hopkinson pressure bar experiment[J]. Science Technology and Engineering, 2014, 14(1): 1-4.

[26] KHAN A S, SUH Y S, KAZMI R. Quasi-static and dynamic loading responses and constitutive modeling of titanium alloys[J]. International Journal of Plasticity, 2004, 20(12): 2233-2248.

[27] 陈 敏. TC4钛合金力学性能测试及动态材料模型研究[D]. 南京: 南京航空航天大学, 2012.

CHEN Min. Research on mechanical properties test and dynamic material model of Ti6Al4V titanium alloy[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012.

Research on parameter estimation of Johnson-Cook constitutive model

SHU Chang¹, CHENG Li¹, XU Yu²

(1. Aeronautics Engineering College, Air Force Engineering University, Xi’an 710038, China;

2. 93152 Unit of People’s Liberation Army of China, Tonghua 134000, China)

Abstract: In order to investigate the mechanical properties of BT3-1 titanium alloy and compare parameter estimation results of Johnson-Cook constitutive model by different algorithms and experimental conditions , the real stress-strain curves of the material were obtained by mechanical properties experiments. A variety of common algorithms were selected to estimate the parameters of the material constitutive model, and the influence of the results was analyzed by different strain rate and temperature data processing methods. The results indicate that the elastic modulus and flow stress of BT3-1 titanium alloy have different sensitivity to variability in the quasi-static compression test, the material has obvious softening effect with temperature, and it is accompanied by a certain strain rate strengthening phenomenon in the SHPB test. The actual strain rate fluctuates around the nominal strain rate, and the actual temperature change is affected by the nominal strain rate and the nominal temperature. Different parameter estimation algorithms will cause different calculation time and estimation results; When estimating the parameters by using the SHPB experiments data, it will result in a large estimated deviation if the nominal strain rate and temperature data are adopted, consideration should be given to temperature changes during the loading process.

Key words: Hopkinson pressure bar experiments; Johnson-Cook constitutive model; optimization algorithm; parameter estimation

Foundation item: Project(2015CB057400) supported by the Major State Basic Research Development Program of China

Received date: 2019-04-15; Accepted date: 2019-11-12

Corresponding author: CHENG Li; Tel: +86-13991321616; E-mail: cheng_qiaochu@foxmail.com

(编辑  何学锋)

基金项目：国家重点基础研究发展计划资助项目(2015CB057400)

收稿日期：2019-04-11；修订日期：2019-11-12

通信作者：程  礼，教授，博士；电话：13991321616；E-mail:cheng_qiaochu@foxmail.com