Combining TOPSIS and GRA for supplier selection problem with interval numbers
来源期刊:中南大学学报(英文版)2018年第5期
论文作者:张萌 LI Guo-xi(李国喜)
文章页码:1116 - 1128
Key words:supplier selection; interval number; grey relational analysis (GRA); technique for order preference by similarity to an ideal solution (TOPSIS)
Abstract: Supplier selection can be regarded as a typical multiple attribute decision-making problem. In real-world situation, the values of the alternative attributes and their weights are always being nondeterministic, and as a result of this, the values are considered interval numbers. In addition, the common approach to measure the similarity between alternatives through their distance suffers from some minor shortcomings. To address these problems, this study develops a novel hybrid decision-making method by combining the technique for order preference by similarity to an ideal solution (TOPSIS) with grey relational analysis (GRA) for supplier selection with interval numbers. By introducing the intervals theory, the extensions of Euclidean distance and grey relational grade are defined. And then a new comprehensive closeness coefficient is constituted for supplier alternatives evaluation based on the interval Euclidean distance and the interval grey relational grade, which could indicate the distance-based similarity and the shape-based similarity simultaneously. A numerical example is taken to validate the flexibility of the proposed method, and result shows that this method can tackle the uncertainty in real-world supplier selection and also help decision makers to effectively select optimal suppliers.
Cite this article as: ZHANG Meng, LI Guo-xi. Combining TOPSIS and GRA for supplier selection problem with interval numbers [J]. Journal of Central South University, 2018, 25(5): 1116–1128. DOI: https://doi.org/10.1007/ s11771-018-3811-y.

J. Cent. South Univ. (2018) 25: 1116-1128
DOI: https://doi.org/10.1007/s11771-018-3811-y
ZHANG Meng(张萌), LI Guo-xi(李国喜)
College of Mechatronic Engineering and Automation, National University of Defense Technology,Changsha 410073, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: Supplier selection can be regarded as a typical multiple attribute decision-making problem. In real-world situation, the values of the alternative attributes and their weights are always being nondeterministic, and as a result of this, the values are considered interval numbers. In addition, the common approach to measure the similarity between alternatives through their distance suffers from some minor shortcomings. To address these problems, this study develops a novel hybrid decision-making method by combining the technique for order preference by similarity to an ideal solution (TOPSIS) with grey relational analysis (GRA) for supplier selection with interval numbers. By introducing the intervals theory, the extensions of Euclidean distance and grey relational grade are defined. And then a new comprehensive closeness coefficient is constituted for supplier alternatives evaluation based on the interval Euclidean distance and the interval grey relational grade, which could indicate the distance-based similarity and the shape-based similarity simultaneously. A numerical example is taken to validate the flexibility of the proposed method, and result shows that this method can tackle the uncertainty in real-world supplier selection and also help decision makers to effectively select optimal suppliers.
Key words: supplier selection; interval number; grey relational analysis (GRA); technique for order preference by similarity to an ideal solution (TOPSIS)
Cite this article as: ZHANG Meng, LI Guo-xi. Combining TOPSIS and GRA for supplier selection problem with interval numbers [J]. Journal of Central South University, 2018, 25(5): 1116–1128. DOI: https://doi.org/10.1007/ s11771-018-3811-y.
1 Introduction
With continual business development, globalized markets become increasingly competitive. Establishing effective supply chain management becomes a critical activity. As an important issue in supplier chain management, supplier selection, which is to determine the best supplier in the supply chain, has become a key strategic consideration in enterprise competition. A good supplier is capable of providing competitive products while obtaining profits. For most manufacturing firms, more than 60% of the production cost is spent for the purchases of raw materials, components, subsystems and components. And for high-tech companies, the percentage is even up to 80%. In addition, approximately 30% of the product quality problems and 80% of the delivery delays are caused by parts suppliers. Moreover, as the manufacturing industry continues to segment, the proportion of product components through purchasing will be further increased, which makes the overall product performance, production cost and delivery time be more dependent on the individual components and their suppliers. Thus, selecting the optimal suppliers reasonably and assembling the provided parts into a final product rapidly will directly affect the enterprises to reduce costs, increase flexibility, and improve competitiveness.
In recent years, researchers have paid considerable attention to supplier selection and a number of studies on supplier selection have been conducted [1–3]. It can be seen from literatures that the supplier selection has experienced the transformation from the single criterion oriented and certain method to the multiple criteria oriented and uncertain method. The ultimate goal of this transformation is to tackle the supplier selection problem in the practical and complex situation. Characteristically, real-world situations are often not deterministic, and some factors such as item price, lead time, quality and reliability are always changing that could inevitably influence the decision-making process of supplier selection. It is inappropriate to ignore these uncertainties existing in supplier selection that will very likely lead to making mistakes. Additionally, using a deterministic model and corresponding algorithm to attempt to solve the problem of supplier selection with uncertainties can cause severe distortion of the result. Hence, it is necessary to study the supplier selection problem under a hybrid uncertainty environment.
The current methods of dealing with uncertainty problems can be grouped into three categories: fuzzy programming, stochastic programming and interval programming. Fuzzy programming models [4] consider the uncertain parameters of the objective functions and constraints fuzzy numbers that requires membership function of the fuzzy number in the first place. Stochastic programming models [5, 6] deal with uncertain parameters as random variables whose probability distribution should be known in advance. However, for the practical and complex supplier selection problem, it is very hard to capture the membership function of the fuzzy number and the probability distribution of the random variable. The interval programming technique is also popular to solve uncertain problems besides the above two techniques which considers the uncertain parameters as interval numbers. The interval-valued parameters, which could be expressed with the lower and upper bounds, are relatively easy to obtain. Moreover, a fuzzy number can be transformed into an interval number by use of the α-cut technique [7] while a random number can also be transformed into an interval number through a given confidence level. Therefore the fuzzy and random parameters could be uniformly expressed via interval numbers and solving the supplier selection problem with interval numbers has a real significance.
Supplier selection problem is usually regarded as a typical multi-attribute decision-making (MADM) problem [8]. MADM problem is to select a most satisfied alternative from a finite number of feasible alternatives based on the values of each attribute with respect to every alternative. A number of methodologies for MADM have been employed to select suppliers, such as simple additive weighting (SAW), analytical hierarchy process (AHP), analytical network process (ANP), elimination and choice expressing reality (ELECTRE), preference ranking organization method for enrichment evaluation (PROMETHEE). Technique for order performance by similarity to ideal (TOPSIS) and grey relational analysis (GRA) are two commonly used decision-making techniques and capable of solving the problem of supplier selection.
TOPSIS was first proposed by HWANG et al [9] for solving MADM problems. This method constructs the positive ideal and negative ideal solutions in the n-dimensional attribute space. The positive ideal solution maximizes the benefit attributes and minimizes the cost attributes. On the other hand, the negative ideal solution minimizes the benefit attributes and maximizes the cost attributes. To measure the distances of the alternatives from the ideal solutions, the optimal alternative can be determined which should have the shortest distance from the positive ideal solution and the farthest from the negative ideal solution. TOPSIS is widely used in diverse fields [10, 11]. In the classical TOPSIS method, the ratings of alternatives and the weights of attributes are presented by real-valued data. Nevertheless, in practice often it is hard to present precisely exact data. Hence, researchers have proposed several extensions of TOPSIS method for solving practical problems under different circumstances, such as fuzzy extension [12–17] and interval extension [18–22].
The GRA method was originally developed by DENG [23] and is suitable for making decision in multiple attribute situation. The advantages of the GRA is related to its ability to capture, process, and integrate uncertainty in the decision making process. GRA solves MADM problems by combining the entire range of attribute values being considered for every alternative into one, single value. This reduces the original problem to a single attribute decision making problem. Therefore, alternatives with multiple attributes can be compared easily after the GRA process [24]. Recently, many researchers have tried to apply GRA to the supplier selection [25–28].
The implementation process of TOPSIS is similar to that of GRA. They all concentrate to measure the similarity between the feasible alternatives and ideal ones. For the TOPSIS method, the distance of an alternative from the ideal solution represents the similarity between them, and the alternative which has a shortest distance from the positive ideal solution and the farthest from the negative ideal solution should be the best choice. On the other side, for GRA, the grey relational grade indicates the similarity between the alternative and the ideal solution. If a comparison number sequence for an alternative gets the greatest grey relational grade with the reference number sequence, it means that the comparison number sequence is most similar to the reference number sequence, and that alternative would be the best one. Here, the reference number sequence is translated from the ideal solution. A curve can be obtained by linking the data points of the number sequence in turn. There are two kinds of similarities between curves: position and shape. The distance adopted in TOPSIS method is inclined to express the position similarity between the number sequences, while the grey relational grade used in GRA mainly focuses on describing the shape similarity between the sequences [29]. These two MADM techniques have their own advantages which can make up each other to improve decision quality. Thus combining TOPSIS and GRA for supplier selection problems is a good concept worthy of serious consideration. SUN et al [30] presented a new decision-making method based on grey correlation degree and TOPSIS, and established a new kind of relative similarity degree by combining the Euclidean distance with grey correlation degree. TRIPATHY et al [31] applied Taguchi method in combination with TOPSIS and GRA to evaluate the effectiveness of optimizing multiple performance characteristics for powder mixed electro-discharge machining. WANG [32] proposed a hybrid decision-making method combining SAW, TOPSIS and GRA, whose average scores were used as responses to construct the regression model for ranking the alternatives. CHEN [33] combined the grey relation model based on the concepts of TOPSIS to evaluate and select the best alternative by introducing the definition of grey relational coefficient to replace the definition of general distance.
On the basis of existing researches, this paper tries to extend the conventional TOPSIS and GRA methods with interval numbers, and proposes a new hybrid interval MADM technique for supplier selection under uncertainty by combining the extended TOPSIS and GRA. This article has the following aims: 1) to tackle the problem of supplier selection when the values of alternative attributes are interval, 2) to constitute a new index to comprehensively measure the similarity between alternatives by integrating the distance of TOPSIS with the grey relational grade of GRA which can reflect both position and shape similarities. The rest of the paper is organized as follows. In the next section, we recall some basic definitions needed for the subsequent analysis. The problem is defined in Section 3, and mathematical model for the supplier selection is developed. The proposed method and procedures for solving the supplier selection problem are described in Section 4. In section 5, a numerical example is discussed to illustrate the practicability of our approach before conclusions are drawn in Section 6.
2 Preliminaries
2.1 Interval number and its operations
An interval number is denoted as 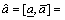
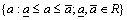 , where
, where 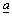 is the lower bound of
is the lower bound of 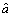 and
and 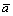 is the upper bound. If
is the upper bound. If 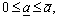 we call interval number
we call interval number 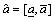 a positive interval number; if
a positive interval number; if  we call it a negative interval number. Suppose that
we call it a negative interval number. Suppose that 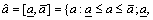
 and
and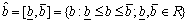 are two arbitrary interval numbers, some basic interval operations can be defined as follows.
are two arbitrary interval numbers, some basic interval operations can be defined as follows.
1) Addition,
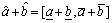 (1)
(1)
2) Subtraction,
 (2)
(2)
3) Multiplication,
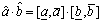
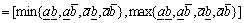 (3)
(3)
Especially, if both 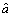 and
and 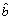 are positive interval numbers, the above equation is simplified as
are positive interval numbers, the above equation is simplified as
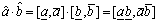 (4)
(4)
4) Division,
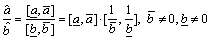 (5)
(5)
Obviously, the reciprocal of an interval number is,
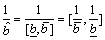 (6)
(6)
5) Exponentiation,
 (7)
(7)
6) Extraction of root,
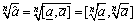 (8)
(8)
where 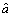 is a positive interval number.
is a positive interval number.
2.2 Comparison of interval numbers
Commonly the degree of possibility is defined to quantitatively compare the ranking of interval numbers [34–36]. If 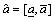 and
and  are two arbitrary interval numbers, the possibility degree of
are two arbitrary interval numbers, the possibility degree of 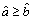 can be expressed as follows:
can be expressed as follows:
 (9)
(9)
There are three possible cases for the position relationship between 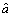 and
and 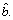 If
If 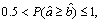 we say that
we say that 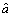 is greater than
is greater than 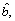 denoted as
denoted as 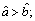 if
if 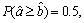 we say that
we say that 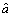 is equal to
is equal to 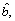 denoted as
denoted as 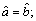 if
if 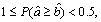 we say that
we say that 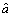 is smaller than
is smaller than 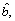 denoted as
denoted as 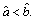 This method makes it possible to calculate the possibility that an interval number is greater or smaller than another one. However, it cannot provide the measure of intervals distance when they have no common area. Therefore, to get a measure of distance between intervals which additionally indicate which interval is greater/smaller, in Ref. [14] proposed a direct parameter is as below.
This method makes it possible to calculate the possibility that an interval number is greater or smaller than another one. However, it cannot provide the measure of intervals distance when they have no common area. Therefore, to get a measure of distance between intervals which additionally indicate which interval is greater/smaller, in Ref. [14] proposed a direct parameter is as below.
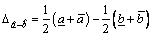 (10)
(10)
It is obvious that the above equation defines the distance between the midpoints of two interval
numbers. The value of 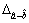 is considered for the interval comparison:
is considered for the interval comparison: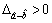 indicates
indicates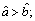
 means
means 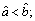
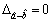 represents
represents 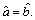
This method makes it easy to calculate the possibility that an interval is greater/smaller than another one when they have a common area and when they do not intersect. Moreover, the distance from the interval number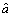 to
to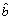 can be simultaneously obtained,
can be simultaneously obtained,
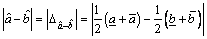 (11)
(11)
3 Problem formulation
Supplier selection is a form of decision- making activity where the optimum supplier is being determined from a finite set of potential alternatives according to some decision criteria, as shown in Figure 1. The first step of the evaluation task is to identify decision criteria. Literatures show that cost, lead time, quality, and reliability comprise the primary criteria utilized by customers mostly to evaluate the suppliers [37]. Thus these four criteria are considered to create an appropriate set of major performance measures.
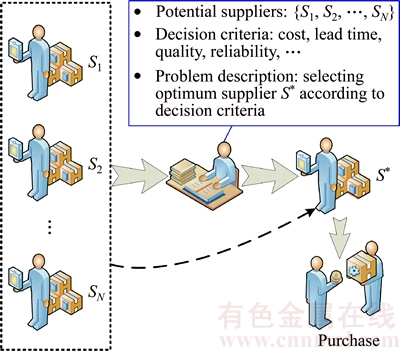
Figure 1 Diagram of supplier selection
Supplier selection can be regarded as a typical multiple attribute decision-making problem. Let 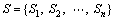 denote the collection of n possible supplier alternatives. Each supplier can be evaluated with respect to a set of m attributes, denoted as
denote the collection of n possible supplier alternatives. Each supplier can be evaluated with respect to a set of m attributes, denoted as 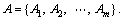 Assume that these attributes are additively independent.
Assume that these attributes are additively independent. 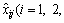
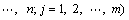 represents the rating of alternative Si with respect to the attribute Aj. In this article,
represents the rating of alternative Si with respect to the attribute Aj. In this article,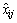 is an interval number, which can be expressed as
is an interval number, which can be expressed as 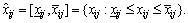
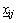 is the lower bound of
is the lower bound of 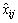 while
while  is the upper bound. All the ratings are assigned to the alternatives and presented in the interval-valued decision matrix, defined as below:
is the upper bound. All the ratings are assigned to the alternatives and presented in the interval-valued decision matrix, defined as below:
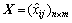
A1A2 … Am
 (12)
(12)
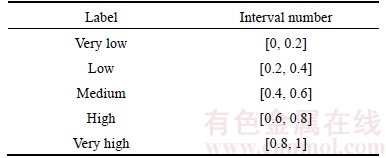
Similarly, in practice often it is hard to present precisely exact weight of each decision attribute. In this paper, the attribute weights are considered linguistic variables. Here, these linguistic variables can be expressed in interval numbers by the 1–5 scale shown in Table 1. Let 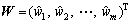 be the vector of attribute weights.
be the vector of attribute weights. 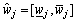
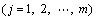 represents the weight of the jth attribute satisfying
represents the weight of the jth attribute satisfying 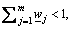
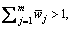
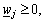

Table 1 Definitions of linguistic variable of attribute weights
Thus, the supplier selection problem turns into a multiple attribute decision making problem that the attribute weights and ratings of suppliers are both interval numbers.
4 Proposed method
4.1 Interval TOPSIS
The conventional TOPSIS method is based on the idea that the best alternative should have the shortest distance from the positive ideal solution and the greatest distance from the negative one. Considering the interval expression of attribute weights and ratings of supplier alternatives, the classical TOPSIS method should be adapted, and then a novel extension of classical TOPSIS method, interval TOPSIS for short, is proposed, which consists of the following steps:
Step 1: Acquire the ratings of supplier alternatives with respect to all attributes, and construct the interval-valued decision matrix 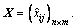
Step 2: Normalize the interval-valued decision matrix as 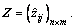 The attributes are classified
The attributes are classified
into two groups: benefit and cost. Benefit attribute (e.g., quality and reliability) means that the greater values are better and the cost attribute (e.g., price and lead time) means that the smaller values are better. For a benefit attribute, 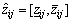 is generated from:
is generated from:
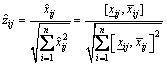

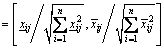 (13)
(13)
For a cost attribute, 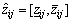 is generated from:
is generated from:
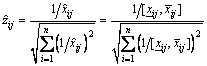

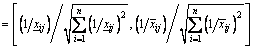 (14)
(14)
This normalization is to transfer the ranges of interval number into [0, 1].
Step 3: Take into account the importance of attributes, and compute the weighted normalized interval-valued decision matrix  using the following expressions:
using the following expressions:
 (15)
(15)
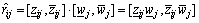 (16)
(16)
Step 4: Determine the positive ideal and negative ideal solution respectively based on the weighted normalized interval-valued decision matrix. In the most of interval extended TOPSIS methods, the upper bound of positive ideal solution is calculated and the lower bound of negative ideal solution is calculated.
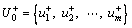
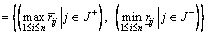 (17)
(17)
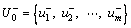
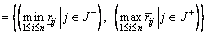 (18)
(18)
In the above equations, J+ is associated with benefit attributes and J– is associated with cost attributes.
The real-valued ideal solutions provided by such formulations are not always attainable in the interval-valued decision matrix. It means that the ideal solutions are “wrong”. Consequently, a more correct and direct approach to calculation of ideal solutions is representing them in the interval form using the expressions [16]:


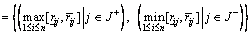 (19)
(19)
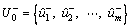
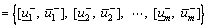
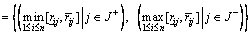 (20)
(20)
It is obvious that the obtained positive and negative interval-valued ideal solutions are fully attainable in the corresponding interval-valued decision matrix. This approach helps to avoid producing “wrong” results. The main difficulty in the implementation of the above method is how to choose the maximal and minimal interval numbers. As elaborated in Section 2.2, Eq. (10) is considered for interval comparison, and then the positive and negative interval-valued ideal solutions can be easily obtained.
Step 5: Obtain the distances of the supplier alternatives from the positive and negative interval-valued ideal solutions. Two distances for each alternative can be respectively calculated using the Euclidean distance as follows:
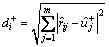
 (21)
(21)
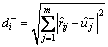
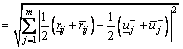 (22)
(22)
Step 6: Calculate the Euclidean distance based relative closeness of each supplier alternative with respect to the ideal solutions, which indicates position similarity between the supplier alternative and the ideal solutions. The bigger the  the better the supplier alternative Si. It means that Si is the closest to the positive ideal solution and the farthest from the negative one.
the better the supplier alternative Si. It means that Si is the closest to the positive ideal solution and the farthest from the negative one.
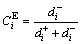 (23)
(23)
Step 7: Rank the supplier alternatives according to the Euclidean distance based closeness coefficient  and select the best one whose relative closeness is the greatest.
and select the best one whose relative closeness is the greatest.
4.2 Interval GRA
The main process of GRA can be summarized as follows: 1) translating the performance of all alternatives into a comparison number sequence, and translating the performance of ideal alternatives into a reference number sequence; 2) calculating the grey relational coefficient between all comparison number sequences and the reference number sequence; 3) calculating the grey relational grade between the reference number sequence and every comparison number sequences based on these obtained grey relational coefficients. When a comparison number sequence translated from an alternative has the highest grey relational grade between the reference number sequence and itself, that corresponding alternative will be the optimal choice. In other words, the problem is to find the alternative whose comparison number sequence is the closest to the reference number sequence. Some adaptations to the traditional GRA are made in this section as the input data are all interval. The implementation procedures of the interval GRA are listed as below:
Steps 1–4 of interval GRA and those of interval TOPSIS are the same.
Step 5: The positive ideal interval-valued solution is considered a positive referential alternative while the possible suppliers are considered compared alternatives. Here, 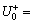
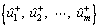 is the sequence of weighted normalized attribute values of the referential alternative, which is called the reference number sequence. Also,
is the sequence of weighted normalized attribute values of the referential alternative, which is called the reference number sequence. Also,  is the sequence of weighted normalized attribute values of the compared alternative Si, which is named the comparison number sequence. Therefore, there will be n comparison number sequences, and each sequence contains m values. Let
is the sequence of weighted normalized attribute values of the compared alternative Si, which is named the comparison number sequence. Therefore, there will be n comparison number sequences, and each sequence contains m values. Let 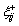 represent the grey relational coefficient of the jth data point (attribute) between the reference number sequence
represent the grey relational coefficient of the jth data point (attribute) between the reference number sequence 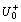 and the comparison number sequence ri, then the grey relational coefficient can be computed as follows:
and the comparison number sequence ri, then the grey relational coefficient can be computed as follows:
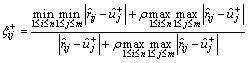
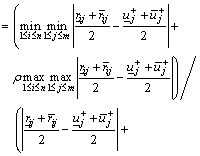
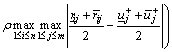 (24)
(24)
where ρ is a value between 0 and 1. The distinguishing coefficient ρ is used to increase the diversity of grey relational coefficients. In general, the value of ρ can be set to 0.5. Thus, a matrix of grey relational coefficient concerning the comparison number sequences and the reference number sequence can be obtained,
 (25)
(25)
Let 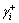 represent the grey relational grade between the comparison number sequence ri and reference number sequence
represent the grey relational grade between the comparison number sequence ri and reference number sequence 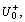 then
then
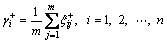 (26)
(26)
The value of 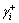 reflects the overall degree of standardized deviance of the comparison number sequence from the reference number sequence. And a comparison number sequence with a high value of
reflects the overall degree of standardized deviance of the comparison number sequence from the reference number sequence. And a comparison number sequence with a high value of 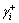 indicates that it has a high degree of consensus on the reference number sequence.
indicates that it has a high degree of consensus on the reference number sequence.
Step 6: Similarly, take the negative ideal interval-valued solution as a negative referential alternative, and consider the possible suppliers as compared alternatives. Then, 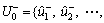
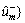 is the reference number sequence and
is the reference number sequence and 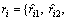
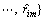 is the ith comparison number sequence. Let
is the ith comparison number sequence. Let 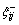 represent the grey relational coefficient of the jth data point between
represent the grey relational coefficient of the jth data point between 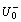 and ri, then the grey relational coefficient can also be calculated,
and ri, then the grey relational coefficient can also be calculated,

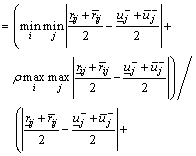
 (27)
(27)
The grey relational grade between the comparison number sequence ri and reference number sequence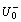 is computed using the following formula,
is computed using the following formula,
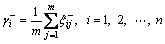 (28)
(28)
Step 7: Calculate the grey relational grade based relative closeness of each comparison number sequence with respect to the reference number sequences, which indicates the shape similarity between the comparison number sequence and reference number sequences. The bigger the 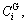 the better the compared supplier alternative Si. It is shown that the curve shape of the number sequence corresponding with Si is the most similar to that of the positive referential alternative and mostly different from that of the negative referential alternative.
the better the compared supplier alternative Si. It is shown that the curve shape of the number sequence corresponding with Si is the most similar to that of the positive referential alternative and mostly different from that of the negative referential alternative.
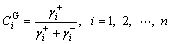 (29)
(29)
Step 8: Rank the supplier alternatives according to the grey relational grade based closeness coefficient 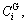 and select the best one whose relative closeness is the greatest.
and select the best one whose relative closeness is the greatest.
4.3 Decision-making model based on combination of Euclidean distance and grey relational grade
There exists a certain degree of similarity between the input and operation of GRA and the multiple attribute evaluation of TOPSIS. However, there are still some differences between them. TOPSIS method is inclined to reflect the position relationship of number sequences which can be measured using the Euclidean distance. GRA mostly indicates the curve shape relationship of number sequences which is computed by the grey relational grade. In order to take into account the position and shape of the data series at the same time, this paper combines the interval TOPSIS method with interval GRA to tackle the supplier selection problem with interval numbers, and constitutes a new hybrid relative closeness to assess the supplier alternatives. This proposed method has the advantages of both TOPSIS and GRA. As shown in Figure 2, the procedures are delineated as follows:
Step 1: Construct the interval-valued decision matrix 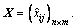
Step 2: Standardize the matrix X with expressions (13), (14), and obtain the normalized interval-valued decision matrix 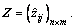
Step 3: Establish the weighted normalized interval-valued decision matrix  using Eqs. (15) and (16).
using Eqs. (15) and (16).
Step 4: Determine the positive interval-valued ideal solution  and negative interval-valued ideal solution
and negative interval-valued ideal solution 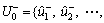
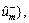 respectively, by using Eqs. (10), (19) and (20).
respectively, by using Eqs. (10), (19) and (20).
Step 5: Compute the two Euclidean distances, 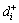 and
and  of each supplier alternative from the positive and negative interval-valued ideal solutions through formulas (21) and (22).
of each supplier alternative from the positive and negative interval-valued ideal solutions through formulas (21) and (22).
Step 6: Compute the two grey relational grades, 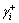 and
and 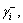 between every comparison number sequence and reference number sequences
between every comparison number sequence and reference number sequences 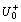 and
and 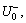 respectively.
respectively.
Step 7: Normalize the Euclidean distances and the grey relational grades obtained from Step 5 and Step 6 as below,
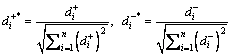
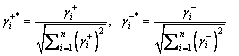 (30)
(30)
The bigger the 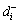 and
and 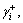 the closer the supplier alternative to the positive interval-value ideal solution in position and shape. Contrarily, the bigger the
the closer the supplier alternative to the positive interval-value ideal solution in position and shape. Contrarily, the bigger the 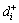 and
and 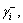 the closer the supplier alternative to the negative interval-value ideal solution in position and shape. Therefore, considering the combination of the normalized Euclidean distances and grey relational grades, a hybrid formulation is established as below in order to express the connection between the supplier alternative and ideal solutions from the position and shape aspects.
the closer the supplier alternative to the negative interval-value ideal solution in position and shape. Therefore, considering the combination of the normalized Euclidean distances and grey relational grades, a hybrid formulation is established as below in order to express the connection between the supplier alternative and ideal solutions from the position and shape aspects.
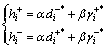 (31)
(31)
In the above formula, α and β are separately the weights of position and shape in the calculation of the similarity degree of the supplier alternative and ideal solutions, reflecting the decision maker’s preference for position and shape factors. The decision maker can adjust the values of α and β according to his preference, satisfying 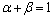
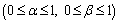 .
.
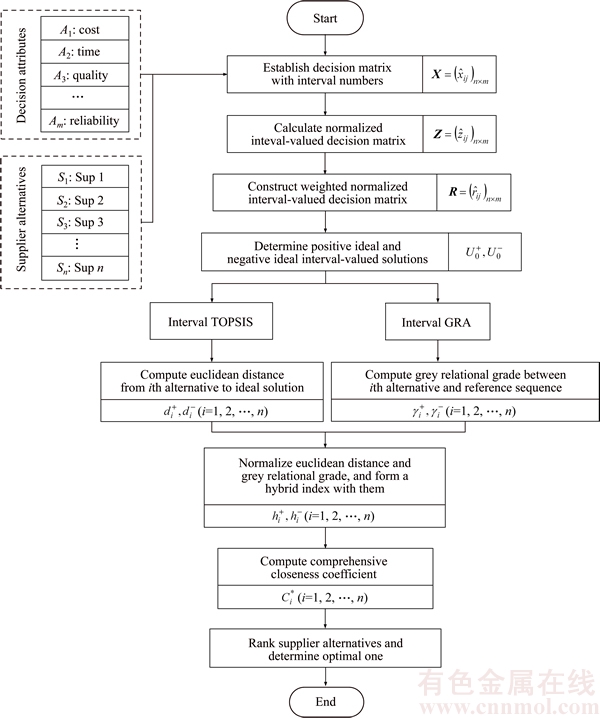
Figure 2 Procedure for proposed methodology
Step 8: Calculate the comprehensive relative closeness of each supplier alternative, which indicates the integrated degree of position and shape similarities between the supplier alternative and the ideal solutions. The bigger the 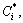 the better the supplier alternative Si.
the better the supplier alternative Si.
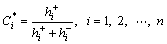 (32)
(32)
Step 9: Rank the supplier alternatives according to the comprehensive closeness coefficient 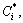 and select the optimal one whose relative closeness is the greatest.
and select the optimal one whose relative closeness is the greatest.
5 Numerical example
To verify the feasibility and effectiveness of the proposed method, let us consider the following example (adopted from Ref. [38] and modified) which can be qualified as a case study. There are five potential suppliers and four decision attributes, denoted as 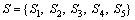 and
and 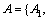
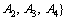 respectively. A1 (price) and A2 (lead time) are the cost attributes while A3 (quality) and A4 (reliability) are the benefit attributes. Assume that the following weights were assigned to the attributes A1–A4 with linguistic variables: Medium, Low, Very high, High. From Table 1, the interval-valued vector of attribute weights can be gotten:
respectively. A1 (price) and A2 (lead time) are the cost attributes while A3 (quality) and A4 (reliability) are the benefit attributes. Assume that the following weights were assigned to the attributes A1–A4 with linguistic variables: Medium, Low, Very high, High. From Table 1, the interval-valued vector of attribute weights can be gotten: 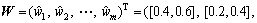
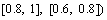 . Using the proposed method to solve this supplier selection problem, the steps are listed as follows.
. Using the proposed method to solve this supplier selection problem, the steps are listed as follows.
Step 1: Establish the interval-valued decision matrix.

Step 2: Calculate the normalized interval- valued decision matrix. Standardizing the original matrix converts the initial divergent measures to a common 0–1 scale. Here we obtain matrix Z as follows.
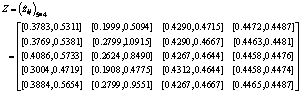
Step 3: Calculate the weighted normalized interval-valued decision matrix R by multiplying the weight interval by matrix Z.
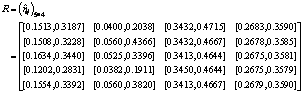
Step 4: Determine the positive and negative interval-valued ideal solutions: 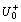 and
and 
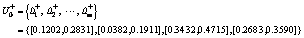
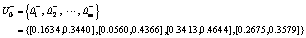
Step 5: Calculate the distances from each supplier alternative to the ideal solutions respectively. We can obtain two collections, D+ and D–.

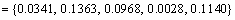

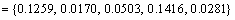
Step 6: Determine the positive and negative reference number sequences 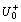 and
and 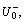 and then calculate the grey relational grades between the comparison number sequence translated from the compared supplier alternative and the two reference number sequences, respectively.
and then calculate the grey relational grades between the comparison number sequence translated from the compared supplier alternative and the two reference number sequences, respectively.
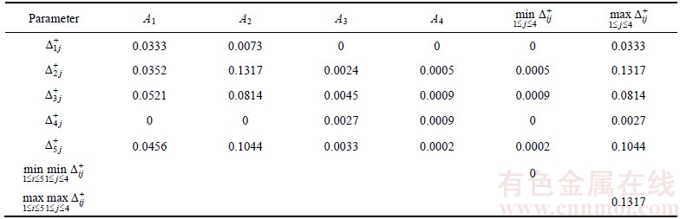
Taking the calculation of grey relational grade between the comparison number sequence and the positive reference number sequence as an example.
Let 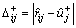 , and we can obtain the values of
, and we can obtain the values of 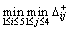 and
and 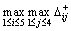 , as shown in Table 2.
, as shown in Table 2.
From the above table, we know that 
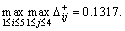 In this example, ρ=0.5. These are used in the calculation of grey relational coefficient. Thus, we can obtain the grey relational coefficient matrix ξ+.
In this example, ρ=0.5. These are used in the calculation of grey relational coefficient. Thus, we can obtain the grey relational coefficient matrix ξ+.
Table 2 Values of 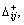
 and
and 

Consequently, the grey relation grade between ri and 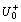 is easy to get.
is easy to get.
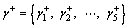
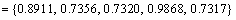
According to the same procedures, we can compute the grey relation grade between ri and 
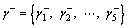
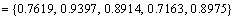
Step 7: Normalize the above distances and relational grades.

Let α=β=0.5, and constitute the hybrid formulas: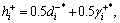
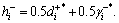 Decision maker can adjust the values of α and β by his personal preference. Thus, we can get the values of
Decision maker can adjust the values of α and β by his personal preference. Thus, we can get the values of 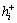 and
and 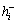 as follows.
as follows.
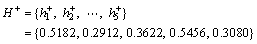
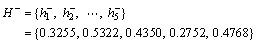
Step 8: Calculate the comprehensive relative closeness of every supplier alternative.
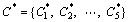
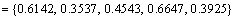
Step 9: Ranking possible supplier alternatives from the greatest to the smallest  obviously, the rank order of supplier alternatives is
obviously, the rank order of supplier alternatives is 
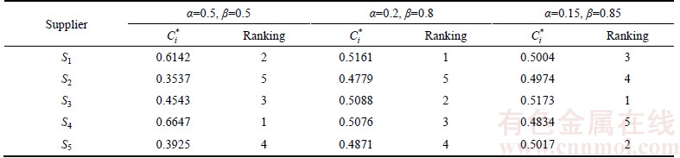
The rank order simultaneously reflects the distance-based similarity and the shape-based similarity between the supplier alternative and the ideal solutions. In general, if the decision maker’s preference for distance-based similarity and shape-based similarity is changing, the supplier alternative ranking result might be different, as shown in Table 3.
6 Conclusions
Supplier selection by its nature involves the presence of uncertain data from multiple suppliers. Actually, the values of the supplier attributes and their weights are always considered interval numbers. In other words, interval numbers are adopted to measure the uncertainty information which is difficult to describe with precise values. Therefore, this article puts forward a new method for supplier selection problem with interval data, which is realized by integrating TOPSIS and GRA. The advantages and contributions of the research are listed as follows.
1) This method is capable of solving the supplier selection problem with the interval situation.
2) By taking into account the position and shape relationships between the supplier alternative and the ideal solutions, the comprehensive relative closeness can embody both distance-based similarity and shape-based similarity.
Table 3 Supplier ranking results under different preferences
3) The ideal solutions, represented in the interval form, are always attainable in the corresponding interval-valued decision matrix, and this is in compliance with basics of conventional TOPSIS method.
4) The method is flexible since the decision maker could adjust distinct values of α and β according to his preference in order to achieve different suppler alternative ranking results.
The methodology has already been applied, tested and validated empirically. It is shown that this novel method provides high robustness, reliability and flexibility for the supplier selection. In practice, there are several types of uncertainties existing in the process of supplier selection. Therefore, the main direction of our future work should focus on selecting suppliers under multiple uncertainties.
References
[1] CHAI J Y, JAMES L N K, ERIC W T N. Application of decision-making techniques in supplier selection: A systematic review of literature [J]. Expert Systems with Applications, 2013, 40(10): 3872–3885. DOI: 10.1016/ j.eswa.2012.12.040.
[2] HO W, XU X W, DEY P K. Multi-criteria decision making approaches for supplier evaluation and selection: A literature review [J]. European Journal of Operational Research, 2010, 202(1): 16–24. DOI: 10.1016/j.ejor.2009.05.009.
[3] JAIN V, WADHWA S, DESHMUKH S G. Select supplier-related issues in modelling a dynamic supply chain: Potential, challenges and direction for future research [J]. International Journal of Production Research, 2009, 47(11): 3013–3039. DOI: 10.1080/00207540701769958.
[4] LIU B D, IWAMURA K. Fuzzy programming with fuzzy decisions and fuzzy simulation-based genetic algorithm [J]. Fuzzy Sets and Systems, 2001, 122(2): 253–262. DOI: 10.1016/S0165-0114(00)00035-X.
[5] CHAINES A, COOPER W W. Chance-constrained programming [J]. Management Science, 1959, 6(6): 73–79. DOI: 10.1287/mnsc.6.1.73.
[6] ABBAS M, BELLAHCENE F. Cutting plane method for multiple objective stochastic integer linear programming [J]. European Journal of Operational Research, 2016, 168(3): 967–984. DOI: 10.1016/j.ejor.2002.11.006.
[7] EL-HAWARY M E. Electric power applications of fuzzy systems [M]. The Institute of Electrical and Electronics Engineers Press, 1998.
[8] GOFFIN K, SZWEJCZEWSKI M, NEW C. Managing suppliers: When fewer can mean more [J]. International Journal of Physical Distribution & Logistics Management, 1997, 27(7): 422–436. DOI: 10.1108/09600039710188486.
[9] HWANG C L, YOON K. Multiple attribute decision making: methods and applications [M]. New York: Springer-Verlag, 1981: 173–184.
[10] BEHZADIAN M, OTAGHSARA S K, YAZDANI M, IGNATIUS J. A state-of the-art survey of TOPSIS applications [J]. Expert Syst Appl, 2012, 39(17): 13051–13069. DOI: 10.1016/j.eswa.2012.05.056.
[11] CHEN Y J. Structured methodology for supplier selection and evaluation in a supply chain [J]. Inf Sci, 2011, 181(9): 1651–1670. DOI: 10.1016/j.ins.2010.07.026.
[12] JAHANSHAHLOO G R, HOSSEINZADE L F, IZADIKHAH M. An algorithmic method to extend TOPSIS for decision making problems with interval data [J]. Applied Mathematics and Computation, 2006, 175(2): 1375–1384. DOI: 10.1016/j.amc.2005.08.048.
[13] JAHANSHAHLOO G R, HOSSEINZADEH L F, DAVOODI A R. Extension of TOPSIS for decision-making problems with interval data: Interval efficiency [J]. Mathematical and Computer Modelling, 2009, 49(5, 6): 1137–1142. DOI: 10.1016/j.mcm.2008.07.009.
[14] JAHANSHAHLOO G R, KHODABAKHSHI M, HOSSEINZADEH L F, MOAZAMI GOUDARZI M R. A cross-efficiency model based on super-efficiency for ranking units through the TOPSIS approach and its extension to the interval case [J]. Mathematical and Computer Modelling, 2011, 53(9): 1946–1955. DOI: 10.1016/j.mcm.2011.01.025.
[15] ZHOU W K, JIANG W C. Two-phase TOPSIS of uncertain multi-attribute group decision-making [J]. Journal of Systems Engineering and Electronics, 2010, 21(3): 423–430. DOI: 10.3969/j.issn.1004-4132.2010.03.012.
[16] OZTAYSI B. A decision model for information technology selection using AHP integrated TOPSIS-Grey: The case of content management systems [J]. Knowledge-Based Systems, 2014, 70(C): 44–54. DOI: 10.1016/j.knosys.2014.02.010.
[17] DYMOVA L, SEVASTJANOV P, TIKHONENKO A. A direct interval extension of TOPSIS method [J]. Expert Systems with Applications, 2013, 40(12): 4841–4847. DOI: 10.1016/j.eswa.2013.02.022.
[18] ANISSEH M, PIRI F, SHAHRAKI M R, AGAMOHAMADI F. Fuzzy extension of TOPSIS model for group decision making under multiple criteria [J]. Artif Intell Rev, 2012, 38(4): 325–338. DOI: 10.1007/s10462-011-9258-2.
[19] TAN C Q. A multi-criteria interval-valued intuitionistic fuzzy group decision making with Choquet integral-based TOPSIS [J]. Expert Systems with Applications, 2011, 38(4): 3023–3033. DOI: 10.1016/j.eswa.2010.08.092.
[20] B Y
Y K
K ZKAN G,
ZKAN G,  G. A combined fuzzy AHP and fuzzy TOPSIS based strategic analysis of electronic service quality in healthcare industry [J]. Expert Syst Appl, 2012, 39(3): 2341–2354. DOI: 10.1016/j.eswa.2011.08.061.
G. A combined fuzzy AHP and fuzzy TOPSIS based strategic analysis of electronic service quality in healthcare industry [J]. Expert Syst Appl, 2012, 39(3): 2341–2354. DOI: 10.1016/j.eswa.2011.08.061.
[21] MOKHTARIAN M N, HADI-VENCHEH A. A new fuzzy TOPSIS method based on left and right scores: an application for determining an industrial zone for dairy products factory [J]. Appl Soft Comput, 2012, 12(8): 2496–2505. DOI: 10.1016/j.asoc.2012.03.042.
[22] DYMOVA L, SEVASTJANOV P, TIKHONENKO A. An interval type-2 fuzzy extension of the TOPSIS method using alpha cuts [J]. Knowledge-Based Systems, 2015, 83(1): 116–127. DOI: 10.1016/j.knosys.2015.03.014.
[23] DENG J L. Introduction to grey system [J]. J Grey Syst, 1989, 1(1): 1–24.
[24] KUO Y, YANG T, HUANG G W. The use of grey relational analysis in solving multiple attribute decision-making problems [J]. Computers & Industrial Engineering, 2008, 55(1): 80–93. DOI: 10.1016/j.cie.2007.12.002.
[25] TSAI C H, CHANG C L, CHEN L. Applying grey relational analysis to the vendor evaluation model [J]. International Journal of the Computer, the Internet and Management, 2003, 11(4): 45–53.
[26] LI G D, YAMAGUCHI D, NAGAI M. A grey-based rough decision-making approach to supplier selection [J]. International Journal of Advanced Manufacturing Technology, 2008, 36(9, 10): 1032–1040. DOI: 10.1007/ s00170-006-0910-y.
[27] YANG C C, CHEN B S. Supplier selection using combined analytical hierarchy process and grey relational analysis [J]. Journal of Manufacturing Technology Management, 2006, 17(7): 926–941. DOI: 10.1108/17410380610688241.
[28] GOLMOHAMMADI D, MELLAT-PARAST M. Developing a grey-based decision-making model for supplier selection [J]. Int J Production Economics, 2012, 137(2): 191–200. DOI: 10.1016/j.ijpe.2012.01.025.
[29] LIU S F, DANG Y G, FANG Z G, et al. Grey system theory and applications [M]. Beijing: Science Press, 2010. (in Chinese)
[30] SUN X D, JIAO Y, HU J S. Research on decision-making method based on grey correlation degree and TOPSIS [J]. Chinese Journal of Management Science, 2005, 13(4): 63–68. (in Chinese)
[31] TRIPATHY S, TRIPATHY D K. Multi-attribute optimization of machining process parameters in powder mixed electro-discharge machining using TOPSIS and grey relational analysis [J]. Engineering Science and Technology, an International Journal, 2016, 19(1): 62–70. DOI: 10.1016/ j.jestch.2015.07.010.
[32] WANG P, ZHU Z Q, WANG Y H. A novel hybrid MCDM model combining the SAW, TOPSIS and GRA methods based on experimental design [J]. Information Sciences, 2016, 345: 27–45. DOI: 10.1016/j.ins.2016.01.076.
[33] CHEN M F, TZENG G H. Combining grey relation and TOPSIS concepts for selecting an expatriate host country [J]. Mathematical and Computer Modelling, 2004, 40(13): 1473–1490. DOI: 10.1016/j.mcm.2005.01.006.
[34] XU Z, CHEN J. Some models for deriving the priority weights from interval fuzzy preference relations [J]. European Journal of Operational Research, 2008, 184(1): 266–280. DOI: 10.1016/j.ejor.2006.11.011.
[35] SEVASTJANOV P. Numerical methods for interval and fuzzy number comparison based on the probabilistic approach and Dempster–Shafer theory [J]. Information Sciences, 2007, 177(21): 4645–4661. DOI: 10.1016/ j.ins.2007.05.001.
[36] WANG Y M, LUO Y. On rank reversal in decision analysis [J]. Mathematical and Computer Modelling, 2009, 49(5, 6): 1221–1229. DOI: 10.1016/j.mcm.2008.06.019.
[37] CELEBI D, BAYRAKTAR D. An integrated neural network and data envelopment analysis for supplier evaluation under incomplete information [J]. Expert Systems with Applications, 2008, 35(4): 1698–1710. DOI: 10.1016/ j.eswa.2007.08.107.
[38] WANG H S, CHE Z H, WANG M J. A three-phase integrated model for product configuration change problems [J]. Experts Systems with Applications, 2009, 36(3): 5491–5509. DOI: 10.1016/j.eswa.2008.06.107.
(Edited by YANG Hua)
中文导读
区间条件下基于理想决策法与灰关联分析的供应商选择方法
摘要:供应商选择属于典型的多属性决策问题。在实际应用中,备选供应商的属性取值以及属性权重通常不是确定数值,而是具有一定的不确定性,一般采用区间数进行表达;另外,传统的采用距离测度度量备选供应商之间相似度的方法存在缺陷。针对这些问题,论文引入区间数理论和灰色系统理论对传统理想解法进行拓展,提出一种基于灰关联分析与理想决策法的区间多属性决策方法,并用于解决供应商选择问题。该方法构建了基于区间数的欧式距离和基于区间数的灰色关联度,通过对二者进行有机结合构造了一种新的综合相对贴近度以实现对备选供应商的定量评价。新贴近度同时反映了备选方案与正理想方案和负理想方案之间的位置关系和数据曲线的形状关系,能够更为准确而全面地反映方案之间的相似或相异程度。最后,通过一个数值算例对所提出的方法进行验证,结果表明该方法能够有效解决实际不确定条件下的供应商选择问题,为决策者选择最佳供应商提供了一种新的技术途径。
关键词:供应商选择;区间数;灰关联分析;理想决策法
Foundation item: Project(51505488) supported by the National Natural Science Foundation of China
Received date: 2016-09-22; Accepted date: 2016-12-08
Corresponding author: ZHANG Meng, PhD, Lecturer; Tel: +86–18673150714; E-mail: zhangmengchn@126.com; ORCID: 0000-0002- 8315-1976

