考虑个体晶粒异质性的微成形材料行为建模
来源期刊:中国有色金属学报(英文版)2020年第11期
论文作者:马振武 彭漩 王春举 曹自洋
文章页码:2994 - 3005
关键词:微成形;尺寸效应;不均匀材料行为;晶粒异质性;复合建模
Key words:micro-forming; size effects; inhomogeneous material behavior; grain heterogeneity; composite modeling
摘 要:以个体晶粒异质性影响为基础建立能够描述微成形中材料变形行为不均匀特性的模型。首先,通过拉伸和显微硬度实验研究个体晶粒异质性对CuZn20箔材变形行为的影响规律。结果显示,与厚板不同,箔材变形区域中的晶粒硬化行为具有不均匀性。箔材的流动应力实际上只反映变形区域中易变形晶粒的平均硬化行为,这是箔材流动应力减小的原因。在此基础上,考虑个体晶粒异质性影响提出一种复合建模方法。分别使用流动应力分类方法和Voronoi剖分法对个体晶粒取向和形状的影响进行表征。该模型为分析个体晶粒异质性对微尺度材料变形行为的影响提供一种准确有效的方法。
Abstract: This study aims to develop a model to characterize the inhomogeneous material deformation behavior in micro-forming. First, the influence of individual grain heterogeneity on the deformation behavior of CuZn20 foils was investigated via tensile and micro-hardness tests. The results showed that different from thick sheets, the hardening behavior of grains in the deformation area of thin foils is not uniform. The flow stress of thin foils actually only reflects the average hardening behavior of several easy-deformation-grains, which is the reason that thinner foils own smaller flow stress. Then, a composite modeling method under consideration of individual grain heterogeneity was developed, where the effects of grain orientation and shape are quantitatively represented by the method of flow stress classification and Voronoi tessellation, respectively. This model provides an accurate and effective method to analyze the influence of individual grain heterogeneity on the deformation behavior of the micro-sized material.
Trans. Nonferrous Met. Soc. China 30(2020) 2994-3005
Zhen-wu MA1, Xuan PENG1, Chun-ju WANG2, Zi-yang CAO1
1. College of Mechanical Engineering, Suzhou University of Science and Technology, Suzhou 215009, China;
2. Robotics and Microsystems Center, School of Mechanical and Electrical Engineering, Soochow University, Suzhou 215131, China
Received 25 March 2020; accepted 11 September 2020
Abstract: This study aims to develop a model to characterize the inhomogeneous material deformation behavior in micro-forming. First, the influence of individual grain heterogeneity on the deformation behavior of CuZn20 foils was investigated via tensile and micro-hardness tests. The results showed that different from thick sheets, the hardening behavior of grains in the deformation area of thin foils is not uniform. The flow stress of thin foils actually only reflects the average hardening behavior of several easy-deformation-grains, which is the reason that thinner foils own smaller flow stress. Then, a composite modeling method under consideration of individual grain heterogeneity was developed, where the effects of grain orientation and shape are quantitatively represented by the method of flow stress classification and Voronoi tessellation, respectively. This model provides an accurate and effective method to analyze the influence of individual grain heterogeneity on the deformation behavior of the micro-sized material.
Key words: micro-forming; size effects; inhomogeneous material behavior; grain heterogeneity; composite modeling
1 Introduction
Miniaturization is an important tendency in many fields including biomedical, aerospace and electronics, so there is a huge demand for micro-scale metallic parts [1-3]. Compared with other micro-manufacturing technologies such as micro-machining and LIGA technique, micro- forming process has aroused extensive attention due to its high production rate, near-net-shapes and excellent products performance [4-6]. The forming theory and material model play key roles in analyzing the material deformation behavior and optimizing the process parameters [7-10]. However, the presence of size effects makes conventional theories and methods inapplicable when analyzing the material deformation behavior in the micro-forming process [11-14].
A great deal of research has been carried out and many new theories have been proposed regarding size effects. Based on the metal physics theory, grains in the surface layer of specimens have at least one free surface, so surface grains represent weaker mechanical behavior than internal grains. On this basis, a classical surface grain theory was proposed, which has been accepted by most researchers because it can explain the size effect phenomenon of “smaller specimen size leading to weaker flow stress” [15-18]. Further- more, MAHABUNPHACHAI and KOC [19] concluded that the influence of grain size, geometric size and feature size should be considered simultaneously when analyzing the micro-sized material deformation behavior. Combining the surface layer theory with the polycrystalline theory, a micro/mesoscale model was developed [20]. It has been revealed that the material behavior in micro-forming is between the single crystal deformation and the polycrystalline deformation. However, as the geometry size of micro-parts decreases to the magnitude of grain size, the influence of individual grain heterogeneity on the deformation behavior of specimens has changed from “ignoring” in forming to “dominating” in micro-forming. The influence of individual grain heterogeneity leads to the inhomogeneous material deformation behavior in many respects, such as the bending characteristics of parts in micro-extrusion process [21], and the unequal feature height of parts in micro-coining process [22,23], so individual grain heterogeneity is an indispensable factor when analyzing the material behavior in micro-forming. However, studies on the deformation behavior of micro-sized materials from the perspective of individual grain heterogeneity are limited.
Furthermore, there is still a lack of systematic studies on the quantitative characterization of the influence of individual grain heterogeneity in micro-forming. In terms of the influence of individual grain shapes, MA et al [24] established a model by using regular hexagons to describe the grain shape for the convenience of calculation, but regular hexagons cannot represent the true shape of grains. In order to accurately analyze the material deformation behavior in micro-forming, multiple sample models need to be established. Considering that the orientation and shape of individual grains have strong randomness, it is difficult to obtain and establish all sample models through scanning electron microscope (SEM) and electron back- scattered diffraction (EBSD). In recent years, the concept of Voronoi polygons has been applied extensively in describing the grain shape [25,26], but further research is still needed to explore the relationship between Voronoi polygons and the microstructure of materials. In terms of the influence of individual grain orientations and positions, pole figures are commonly applied to expressing the effects of grain orientations. However, this method requires high-energy synchrotron radiation sources, resulting in its high cost and equipment dependence in practical application.
Therefore, this research aims to study the influence of individual grain heterogeneity on the deformation behavior of micro-sized materials in depth and then develop an accurate modeling method. First, tensile and micro-hardness tests were carried out to investigate the size effects on the deformation behavior of CuZn20 foils. Then, a composite modeling method under consideration of the heterogeneity of both the grain shape and grain orientation was proposed.
2 Experimental
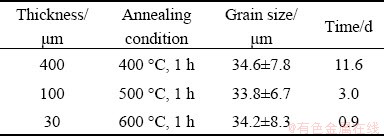
CuZn20 foils with a purity of 99.9% and different thicknesses from 30 to 400 μm were used to conduct tensile tests. The tensile test was designed according to the ASTM E8 standard, and the gauge length and initial width for all specimens were kept constant at 50 mm and 12.5 mm, respectively. In order to improve the clamping stability, fine sandpaper was pasted on both ends (outside the gauge length) of the 30 μm foil specimen. In order to obtain similar grain sizes and eliminate the effect of rolling hardening, foils were subjected to adequate recrystallization annealing at different temperatures for different time in a vacuum furnace. The intercept line method was used to measure the average grain size of foil specimens. The material parameters and correlated annealing conditions are listed in Table 1. The flow stress of CuZn20 foils was determined by averaging the data of six specimens of each thickness.
Table 1 Annealing conditions and material parameters of CuZn20 foils
After deformation, the Vickers hardness of specimens was tested with the micro-hardness tester (HVS-10E). All specimens were mounted, polished, and etched before testing. The test was carried out by holding the pressure for 10 s under a load of 10 g. The indentation was ensured to be pressed in the interior of grains to avoid the influence of grain boundary impurities on the hardness value (Fig. 1). Three specimens were tested in each group. The contour maps in this research were drawn by MATLAB software according to the coordinates and the hardness values of indention points.

Fig. 1 Schematic diagram of micro-hardness test
3 Results and discussion
The true stress-true strain curves of CuZn20 foils are shown in Fig. 2, indicating that the flow stress of foil specimens and the true strain at the breaking point decrease with the decrease of foil thickness. Besides, the standard deviation (SD), namely the scatter of flow stress, increases with decreasing the foil thickness.
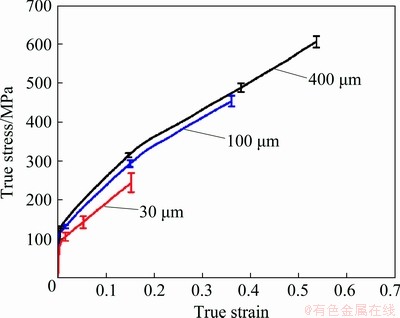
Fig. 2 True stress-true strain curves of CuZn20 foils with different thicknesses
The foil specimens with thicknesses of 400 and 30 μm after fracture are shown in Fig. 3. It can be seen that the fracture behavior of all 400 μm specimens is consistent, with the fracture located within the gauge length and close to the middle of the specimen. In contrast, the fracture behavior of the 30 μm specimens shows strong scatter, and the fractures appear both inside and outside the gauge length. Furthermore, compared with the undeformed region, the 400 μm specimens rather than 30 μm specimens show obvious necking phenomenon. The above results exhibit a distinct size effect phenomenon.
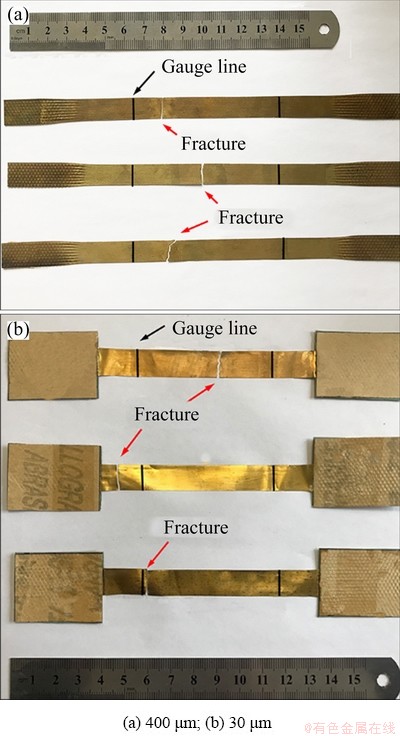
Fig. 3 Photos of specimens after fracture with different thicknesses
3.1 Flow stress and true strain
Since the deformation degree of a material has a positive correlation with its hardness, the hardness distribution can characterize the material deformation distribution. Nearly 330 and 40 indention points were used to construct the contour maps of foils with thicknesses of 400 and 30 μm, respectively. As shown in Fig. 4(a), the hardness distribution of foil specimens with a thickness of 400 μm is basically consistent and corresponding to their fracture locations. The hardness value at the fracture position is the highest, and gradually weakens to both sides. In contrast, the hardness distribution of the 30 μm specimens is disordered, which is relevant to the hardness value of individual grains (Fig. 4(b)). In general, the relatively uniform hardness distribution of the 400 μm specimens indicates that the grains in the deformation area have undergone a homogeneous hardening behavior during the deformation process. However, the hardness distribution of the 30 μm specimens exhibits block characteristics, which means that the hardening behaviors of grains in the deformation area are different.
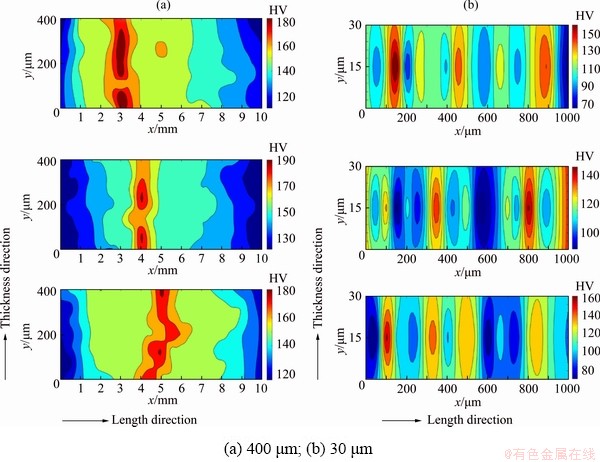
Fig. 4 Hardness distribution maps of foils with different thicknesses
Because of the crystal structure characteristics, along the loading direction, soft oriented grains are much easier to deform than hard oriented grains. Besides, the deformation of soft oriented grains is usually originated from the joint region of grain-boundaries or the position where the grain shape has a sudden change. Therefore, grains that own soft orientations or unique shapes are much easier to deform than other ones. Since the deformation performs in the way of minimizing energy consumption [11], an easy-deformation- chain can be obtained by overlapping easy- deformation-grains in the material during the process of plastic deformation. As shown in Fig. 5(a), for foils that own numerous grains, easy-deformation-grains and difficult-deformation-grains evenly distribute in the deformation area, so it is hard to form the easy-deformation-chain.
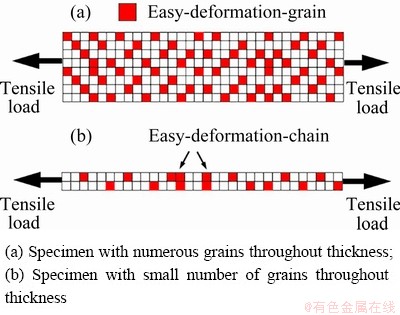
Fig. 5 Schematic of formation of easy-deformation-chain
Besides, the rotation and deformation of grains occur during the process of plastic deformation, which causes difficult-deformation-grains to be involved in the deformation. In other words, all grains of thick foils in the deformation area can participate in the deformation, leading to the homogeneous deformation (Fig. 3(a) and Fig. 4(a)). Therefore, the flow stress of thick foils reflects the average hardening behavior of all grains in the deformation area. However, as the foil thickness decreases, it is easier to form the easy-deformation- chain because of the small grain number in the thickness direction (Fig. 5(b)). Besides, with the decrease of grain number in foils, the compatibility between adjacent grains becomes worse and it is difficult to transfer the dislocation pile-up among grains, so it is much more difficult or even impossible for difficult-deformation-grains to participate in the deformation. Therefore, once this easy-deformation-chain is established, remarkable deformation will occur and concentrate on several easy-deformation-grains, eventually leading to the premature fracture. This may be the reason that the 30 μm foil has very small true strain (Fig. 2) and its hardness distribution shows block characteristics (Fig. 4(b)). In a word, for thin foils, only a small number of grains can participate in the deformation, so their flow stress actually only reflects the average hardening behavior of several easy- deformation-grains, which is the root cause of their low flow stress.
3.2 Inhomogeneous deformation behavior
According to the above analysis, the smaller the number of grains in the deformation area, the easier it is to form the easy-deformation-chain, so the deformation is more concentrated. From the microstructure of the 30 μm foil specimen (Fig. 6), it can be observed that there is only one grain throughout the thickness and grains along the length direction are all different in shapes and orientations. If some grains are in the soft orientation or in the stress concentration region, they will undertake a mass of deformation and dominate the property of foils. Therefore, soft grains and the stress concentration region, or rather, the orientation and shape of individual grains both play key roles in determining the property of the whole material. It is noteworthy that grain orientation and shape both appear randomly, thus resulting in the significant difference in the microstructure of thin foils, even if foil specimens have the same thickness. This is the reason why foils with a small thickness show a large scatter of flow stress and fracture behavior. However, as to thick foils, such as the foil specimen with a thickness of 400 μm, it is difficult to form the easy-deformation-chain because there are numerous grains randomly distributing in the deformation area, so the deformation cannot focus on one specific grain. The influence of individual grain shape and orientation is so little that the difference in the microstructure of foils can be neglected. Therefore, thick foil specimens of the same material exhibit homogeneity and their flow behavior shows similarity.

Fig. 6 Microstructure of foil specimen with thickness of 30 μm
Based on the above analysis, it can be concluded that as the foil thickness decreases, the deformation mode of foils changes from the uniform deformation of all grains in the deformation area to the concentrated deformation of grains in the easy-deformation-chain. The dramatic increase of heterogeneity effects of individual grain orientations and shapes induces an increasing inhomogeneous deformation behavior, which is the root cause of size effects of foil deformation behavior.
4 Modeling of individual grain hetero- geneity
4.1 Characterization of influence of grain orientation
Based on the hardening behavior of individual grains, the mechanical behavior of individual grains can be divided into seven groups and the proportion of each group of individual grains follows the normal distribution [27,28]. In addition, the heterogeneity of individual grain orientation can be expressed as follows. Each grain owns unique flow stress, and the average flow stress of individual grains can take the same value with the average flow stress of material in model building [28,29].
An estimation method for the flow stress of individual grains is proposed, which is described as follows:
(1) The average and the standard deviation (SD) of flow stress are obtained by mechanical experiments (the number of grains is not less than five).
(2) Estimating the upper bound and lower bound of the flow stress for the individual grain. As shown in Fig. 7, the maximum, average, and minimum values of the flow stress for specimens with specific geometric and grain sizes can be obtained by experiments. It is assumed that one specimen contains only three groups of grains, that is, grains with the maximum flow stress, grains with the average flow stress, and grains with the minimum flow stress, and the flow stress of one specimen is produced by combining the flow stress of two different individual grains with equal contribution. Then, the upper (lower) bound of the flow stress for the individual grain can be calculated from the upper (lower) bound of the flow stress for the specimen with the SD of flow stress.
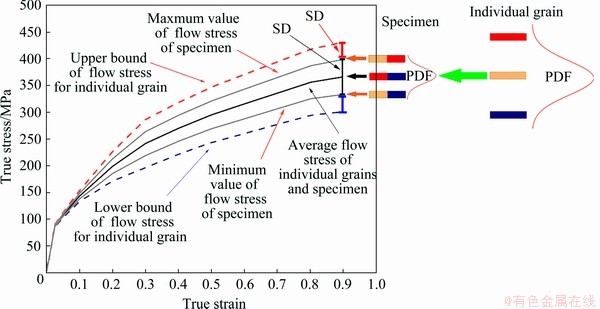
Fig. 7 Estimation of upper bound and lower bound of individual grain flow stress curves (PDF-Probability density function)
(3) Dividing the flow stress of individual grains into seven groups. The flow stress of individual grains is divided into seven groups averagely in the interval of the estimated upper and lower bounds of individual grain flow stress, as shown in Fig. 8.

Fig. 8 Dividing flow stress of individual grains into seven groups
(4) Calculating the proportions of seven groups of individual grains according to the normal distribution law and the probability density function (PDF). The proportion of individual grains in each group is given in Table 2.
Table 2 Proportion of individual grains in each group

4.2 Characterization of influence of grain shape
Based on the geometric similarity between the grain shape and the Voronoi polygons, a method for generating high-fidelity Voronoi polygons of materials is proposed. Taking the generation of two-dimensional Voronoi polygons as an example and assuming that the material has a length L, a width W, and a grain size d, the Voronoi tessellation method is described as follows:
(1) Generate a rectangle with length L and width W, and then equally divide this rectangle into several congruent rectangular cells with the length of 2a and the width of 2b. Therefore, the number of cells in the length direction (NL) is L/(2a), and the number of cells in the width direction (NW) is W/(2b).
(2) Assuming that the coordinates of the center point of a cell are (x, y), a seed point is randomly arranged within the cell. To achieve the interventional control of seed point placement, the seed point is restricted within a control rectangle with diagonal vertices (x-αa, y-βb) and (x+αa, y+βb), where α and β are the distribution control coefficients of the seed point.
(3) It is assumed that the distribution of the seed point within the control rectangle is random. Taking the random numbers μ and ν (0≤μ, ν<1), the coordinates of the seed point in the control rectangle can be expressed as (x+αa(2μ-1), y+βb(2ν-1)).
(4) According to the seed arrangement rule described above, Voronoi polygons of the material are generated by MATLAB software.
It is assumed that the distribution probability of seed points in the length and width direction of rectangular cells is equal, that is, 2a=2b=d and α=β. By inputting different values of the scatter factor α′, Voronoi polygons with different morphologies can be obtained. The generated Voronoi polygons are shown in Fig. 9, indicating that as the value of the scatter factor α′ increases, the scatter degree of the generated Voronoi polygons increases.
The topology information of Voronoi polygons is extracted and then input to the autoCAD software. The sizes of Voronoi polygons are statistically measured by the intercept line method. Under a certain value of scatter factor α′, the variation coefficient of the size of Voronoi polygons is calculated as
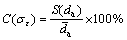 (1)
(1)
where S(da) is the SD of the size of Voronoi polygons d, and 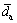 is the average value of the size of Voronoi polygons d.
is the average value of the size of Voronoi polygons d.
The relationship between the variation coefficient of the size of Voronoi polygons and the scatter factor α′ is shown in Fig. 10.
After establishing the relationship between the variation coefficient of the size of Voronoi polygons and the scatter factor α′, the high-fidelity Voronoi polygons of a certain material can be generated according to the microstructure of the material. The specific procedures are described in the following by taking the generation of Voronoi polygons of CuZn20 foils with a thickness of 100 μm as an example. First, the average grain size and its SD are obtained based on the metallography analysis of the experimental specimen (Table 1). Then, the value of variation coefficient is calculated based on Eq. (1), which is 19.8% for this CuZn20 foil specimen. Therefore, the value of the scatter factor α′ can be obtained according to the established relationship (Fig. 10) using the semi-inverse method, which is 0.62. Finally, based on the size of the specimen and the value of scatter factor α′, Voronoi polygons are generated by MATLAB software. The comparison between generated Voronoi polygons and the microstructure of foil specimen is shown in Fig. 11, indicating that generated Voronoi polygons have high similarities to the microstructure of the foil.

Fig. 9 Generated Voronoi polygons
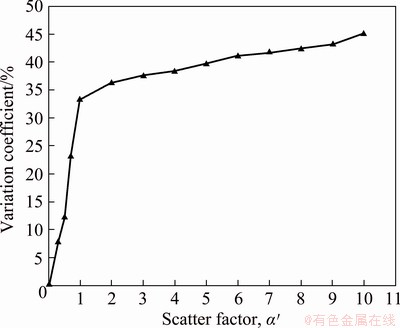
Fig. 10 Relationship between variation coefficient of size of Voronoi polygons and scatter factor α′
4.3 Application
4.3.1 Calculation of flow stress

Fig. 11 Comparison of generated Voronoi polygons (a) and microstructure of foils with thickness of 100 μm (b)
A set of micro-bulk upsetting experiments from literature are used to evaluate whether the proposed method can analyze the scatter characteristics of the flow stress of the material [28]. Relevant experimental parameters are given in Table 3.
Table 3 Experimental parameters of micro-bulk upsetting experiment

According to the estimation method of the flow stress for individual grain proposed in Section 4.1, the flow stress of seven groups of individual grains is estimated based on the flow stress of copper specimens. Moreover, according to the description of individual grain shape proposed in Section 4.2, Voronoi polygons of the base material are generated using the material parameters in Table 3. Then, as shown in Fig. 12, the mechanical properties of the base material can be obtained by assigning the flow stress of seven groups of individual grains into each Voronoi polygon of the base material randomly. In the randomization process, the proportion of individual grains is in accordance with Table 2. After that, sample models are randomly extracted from the base material according to the cross-sectional dimension of the copper specimen, as shown in Fig. 12. Therefore, the flow stress of extracted sample models is calculated:
 (2)
(2)
where n is the number of grains in the sample model, vi is the proportion of the ith grain in the sample model, and σ(ε)i is the flow stress of the ith grain.
The calculated flow stress curves of six sample models extracted from the two base materials with the grain size of 40 and 180 μm are shown in Figs. 13(a) and 13(b), respectively. In general, the calculated flow stress curves of six sample models in two base materials both show the scatter behavior. Moreover, as the grain size increases from 40 to 180 μm, the scatter degree of calculated flow stress curves intensifies but the average value of calculated flow stress significantly reduces. Besides, when comparing the experimental results and calculated values of flow stress, as to the base material with grain size of 40 μm, the distribution of calculated flow stress for six sample models matches the SD of experimental flow stress very well. When the grain size increases to 180 μm, the distribution range of calculated flow stress is less than the SD of experimental flow stress. In an investigation of the friction behavior in micro- forming, DENG et al [30] found that the friction increases sharply with the decrease of grain numbers in the sample. The method proposed in this research does not consider the contact and friction behavior between the specimen and die surface, which may be the cause of the difference between calculated values and experimental results. Nonetheless, the calculated values of flow stress are in good agreement with the experimental results.

Fig. 12 Extraction of sample models from different base materials

Fig. 13 Comparison between calculated values and experimental results of flow stress
4.3.2 Analysis of material deformation distribution
To verify the effectiveness of the proposed method in analyzing the size effects on material deformation distribution, the tensile tests of CuZn20 foils with a thickness of 400 and 30 μm conducted in this research are simulated by ABAQUS/standard, respectively. The heterogeneity effects of both shapes and orientations of individual grains are considered in the modeling process. According to the estimation method of the flow stress for individual grain proposed in Section 4.1, the flow stress curves of seven groups of grains are estimated based on the experimental flow stress of CuZn20 foils and introduced into the ABAQUS/property module. Meanwhile, according to the representation method of individual grain shape proposed in Section 4.2, Voronoi polygons of foils are generated using the material parameters in Table 1 and introduced into the ABAQUS/part module. Then, according to the proportion of each group of individual grains given in Table 2, the mechanical properties of seven groups of individual grains are randomly assigned to Voronoi polygons of foil specimens in the ABAQUS/Property module. CAX4R element is used in the simulation. The serviceable load and displacement are applied to the finite element (FE) models.
The simulation results of deformation distribution for the foil with a thickness of 400 μm are shown in Fig. 14(a), indicating that the equivalent plastic strain (PEEQ) is evenly distributed along the length direction of the specimen. The width in the middle of the specimen is significantly less than the width at both ends, demonstrating that the specimen has undergone a large amount of deformation. Moreover, there is an obvious necking phenomenon in the middle of the specimen. In addition, the deformation distribution states in four simulations are similar.
The simulation results for the foil with a thickness of 30 μm are shown in Fig. 14(b). It can be seen that the PEEQ of four simulated specimens is disordered and exhibits block characteristics. The specimen width changes little along the length direction, and the necking phenomenon before fracture is not obvious, which proves that the specimen produces small deformation before fracture. In addition, the fracture position of the specimen appears randomly. The above simulation results are in good agreement with the tensile and micro-hardness test results (Figs. 3 and 4).
In addition, it is found that the tensile fracture surfaces in Fig. 3 are inclined slightly to the tensile direction, which is not as obvious as that in Fig. 14. In order to characterize the influence of grain orientation, the mechanical behavior of individual grains is divided into seven groups in modeling, but this is not enough to cover all grain orientation types. In the actual deformation process, there are some grains in extremely soft orientation and a large amount of deformation will be concentrated in these grains after the load is applied, so the deformation is difficult to transfer to other grains, causing rapid fracture of the specimen. Moreover, it is difficult to make the specimen axial and tensile direction completely parallel during experiments because the foil is too thin to be clamped, and slight vibration can also cause rapid fracture of the foil specimen. In contrast, the deformation amount of the specimen during the simulation process is larger than that under the experimental condition. Therefore, the fracture inclination of the specimen by simulation is greater than that of the experimental result. These may be the reasons that the fracture phenomenon by experiments is not as obvious as the simulation result.
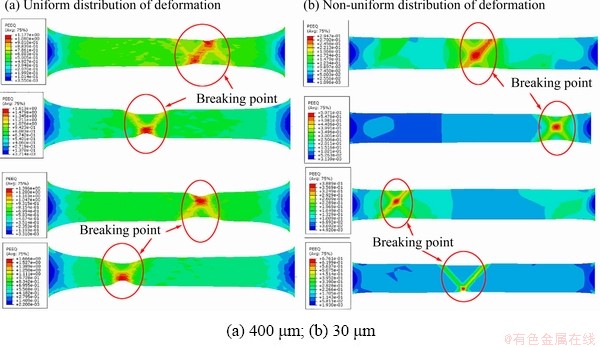
Fig. 14 Simulation results of deformation distribution for foil with different thicknesses
5 Conclusions
(1) As the foil thickness decreases, the deformation mode of foils changes from the uniform deformation of all grains in the deformation area to the concentrated deformation of grains in the easy-deformation-chain.
(2) The flow stress of thin foils actually only reflects the average hardening behavior of several easy-deformation-grains, which is the reason why thinner foils own smaller flow stress.
(3) An efficient estimation method for the flow stress of individual grains is proposed.
(4) High-fidelity Voronoi polygons are generated according to the microstructure of material.
(5) A composite modeling method under consideration of individual grain heterogeneity is developed. The size effects on the material deformation behavior in micro-forming can be analyzed accurately with this method.
References
[1] WANG Chun-ju, WANG Chuan-jie, GUO Bin, SHAN De-bin. Effects of tribological behavior of DLC film on micro-deep drawing processes [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 2877-2882.
[2] MA Zhen-wu, CAO Zi-yang, LU Jin-bin, LI Hua, ZHANG Yang-jing, LIU Wei, YIN Zhen. Size effects on springback behavior of H80 foils [J]. Rare Metals, 2018, 37: 1082-1090.
[3] SHI Yi, ZHANG Wei-zhao, CAO Jian, EHMANN K F. Experimental study of water jet incremental micro-forming with supporting dies [J]. Journal of Materials Processing Technology, 2019, 268: 117-131.
[4] LI Qi-yue, LIU Kai, LI Xi-bing, WANG Ze-wei, WENG Lei. Cutting parameter optimization for one-step shaft excavation technique based on parallel cutting method [J]. Transactions of Nonferrous Metals Society of China, 2018, 28: 1413-1423.
[5] TIWARY A P, PRADHAN B B, BHATTACHARYYA B. Study on the influence of micro-EDM process parameters during machining of Ti-6Al-4V superalloy [J]. The International Journal of Advanced Manufacturing Technology, 2015, 76: 151-160.
[6] XU Jie, GUO Bin, SHAN De-bin. Blanking clearance and grain size effects on micro deformation behavior and fracture in micro-blanking of brass foil [J]. International Journal of Machine Tools and Manufacture, 2012, 60: 27-34.
[7] CHAN Wai-lun, FU Ming-wang. Experimental and simulation based study on micro-scaled sheet metal deformation behavior in micro-embossing process [J]. Materials Science and Engineering A, 2012, 556: 60-67.
[8] LI He-zong, DONG Xiang-huai, SHEN Yu, DIEHL A, HAGENAH H, ENGEL U, MERKLEIN M. Size effect on springback behavior due to plastic strain gradient hardening in micro-bending process of pure aluminum foils [J]. Materials Science and Engineering A, 2010, 527: 4497-4504.
[9] LIU Jian-guang, FU Ming-wang, LU J, CHAN Wai-lun. Influence of size effect on the springback of sheet metal foils in micro-bending [J]. Computational Materials Science, 2011, 50: 2604-2614.
[10] CHENG Li-dong, WANG Chuan-jie, WANG Chun-ju, GUO Bin, WANG Zhen-long. Size effects on plastic deformation behavior in micro radial compression of pure copper [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 2686-2691.
[11] MA Zhen-wu, CAO Zi-yang, LU Jin-bin, LI Hua, ZHANG Yuan-jing, LIU Wei, YIN Zhen. Material flow behavior modeling with consideration of size effects [J]. Rare Metals, 2018, 37: 995-1002.
[12] LIU Jian-guang, FU Ming-wang, LU J, CHAN Wai-lun. A constitutive model for modeling of the deformation behavior in microforming with a consideration of grain boundary strengthening [J]. Computational Materials Science, 2012, 55: 85-94.
[13] SHEN Yu, YU Hu-ping, RUAN Xue-yu. Discussion and prediction on decreasing flow stress scale effect [J]. Transactions of Nonferrous Metals Society of China, 2006, 16: 132-136.
[14] PENG Lin-fa, LIU Fang, NI Jun, LAI Xin-ming. Size effects in thin sheet metal forming and its elastic–plastic constitutive model [J]. Materials & Design, 2007, 28: 1731-1736.
[15] EICHENHUELLER B, EGERER E, ENGEL U. Microforming at elevated temperature-forming and material behaviour [J]. The International Journal of Advanced Manufacturing Technology, 2007, 33: 119-124.
[16] KALS T A, ECKSTEIN R. Miniaturization in sheet metal working [J]. Journal of Materials Processing Technology, 2000, 103: 95-101.
[17] VOLLERTSEN F, HU Z, NIEHOFF H S, THEILER C. State of the art in micro forming and investigations into micro deep drawing [J]. Journal of Materials Processing Technology, 2004, 151: 70-79.
[18] ENGEL U, ECKSTEIN R. Microforming—From basic research to its realization [J]. Journal of Materials Processing Technology, 2002, 125: 35-44.
[19] MAHABUNPHACHAI S, KOC M. Investigation of size effects on material behavior of thin sheet metals using hydraulic bulge testing at micro/meso-scales [J]. International Journal of Machine Tools and Manufacture, 2008, 48: 1014-1029.
[20] LAI Xin-min, PENG Lin-fa, HU Peng, LAN Shu-huai, NI Jun. Material behavior modelling in micro/meso-scale forming process with considering size/scale effects [J]. Computational Materials Science, 2008, 43: 1003-1009.
[21] WANG Chun-ju, SHAN De-bin, ZHOU Jian, GUO Bin, SUN Li-ning. Size effects of the cavity dimension on the microforming ability during coining process [J]. Journal of Materials Processing Technology, 2007, 187: 256-259.
[22] KRISHNAN N, CAO J, DOHDA K. Study of the size effect on friction conditions in micro-extrusion—Part I: Micro-extrusion experiments and analysis [J]. Journal of Manufacturing Science and Engineering, 2007, 129: 669-676.
[23] WANG Guang-chun, ZHENG Wei, WU Tao, JIANG Huai-dong, ZHAO Guo-qun, WEI Dong-bin, JIANG Zheng-yi. A multi-region model for numerical simulation of micro bulk forming [J]. Journal of Materials Processing Technology, 2012, 212: 678-684.
[24] MA Zhen-wu, TONG Gguo-quan, CHEN Feng. Deformation behavior of materials in micro-forming with consideration of intragranular heterogeneities [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 616-626.
[25] ZHANG Hai-ming, LIU Juan, SUI Da-shan, CUI Zhen-shan, FU Ming-wang. Study of microstructural grain and geometric size effects on plastic heterogeneities at grain-level by using crystal plasticity modeling with high-fidelity representative microstructures [J]. International Journal of Plasticity, 2018, 100: 69-89.
[26] SUN Feng-wei, MEADE E D, O'DOWD N P. Strain gradient crystal plasticity modelling of size effects in a hierarchical martensitic steel using the Voronoi tessellation method [J]. International Journal of Plasticity, 2019, 119: 215-229.
[27] LU Hai-na, WEI Dong-bin, JIANG Zheng-yi, LIU Xiang-hua, MANABE K. Modelling of size effects in micro-forming process with consideration of grained heterogeneity [J]. Computational Materials Science, 2013, 77: 44-52.
[28] CHAN Wai-lun, FU Ming-wang, LU J, LIU Jian-gang. Modeling of grain size effect on micro deformation behavior in micro-forming of pure copper [J]. Materials Science and Engineering A, 2010, 527: 6638-6648.
[29] CHAN Wai-lun, FU Ming-wang. Geometry and grain size effects on the fracture behavior of sheet metal in micro-scale plastic deformation [J]. Materials & Design, 2011, 32: 4738-4746.
[30] DENG Jiang-hua, FU Ming-wang, CHAN Wai-lun. Size effect on material surface deformation behavior in micro-forming process [J]. Materials Science and Engineering A, 2011, 528: 4799-4806.
马振武1,彭 漩1,王春举2,曹自洋1
1. 苏州科技大学 机械工程学院,苏州 215009;
2. 苏州大学 机电工程学院 机器人与微系统研究中心,苏州 215131
摘 要:以个体晶粒异质性影响为基础建立能够描述微成形中材料变形行为不均匀特性的模型。首先,通过拉伸和显微硬度实验研究个体晶粒异质性对CuZn20箔材变形行为的影响规律。结果显示,与厚板不同,箔材变形区域中的晶粒硬化行为具有不均匀性。箔材的流动应力实际上只反映变形区域中易变形晶粒的平均硬化行为,这是箔材流动应力减小的原因。在此基础上,考虑个体晶粒异质性影响提出一种复合建模方法。分别使用流动应力分类方法和Voronoi剖分法对个体晶粒取向和形状的影响进行表征。该模型为分析个体晶粒异质性对微尺度材料变形行为的影响提供一种准确有效的方法。
关键词:微成形;尺寸效应;不均匀材料行为;晶粒异质性;复合建模
(Edited by Bing YANG)
Foundation item: Project (51905362) supported by the National Natural Science Foundation of China; Projects (19KJB460022, 18KJB130006) supported by the Natural Science Foundation of Jiangsu Higher Education Institution, China
Corresponding author: Zi-yang CAO; Tel: +86-512-68320560; E-mail: dukeczy@nuaa.edu.cn
DOI: 10.1016/S1003-6326(20)65437-1

