J. Cent. South Univ. (2020) 27: 2455-2464

DOI: https://doi.org/10.1007/s11771-020-4461-4

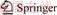
Analysis of ground vibrations induced by high-speed train moving on pile-supported subgrade using three-dimensional FEM

GAO Guang-yun(高广运)^{1, 2}, BI Jun-wei(毕俊伟)^{1, 2},CHEN Qing-sheng(陈青生)^{2, 3}, CHEN Run-min(陈润民)^{1, 2}

1. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China;

2. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education,Tongji University, Shanghai 200092, China;

3. School of Civil Engineering, Architecture and Environment, Hubei University of Technology,Wuhan 430068, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: The pile-supported subgrade has been widely used in high-speed railway construction in China. To investigate the ground vibrations of such composite foundation subjected to moving loads induced by high-speed trains (HSTs), three-dimensional (3D) finite element method (FEM) models involving the pile, pile cap and cushion are established. Validation of the proposed model is conducted through comparison of model predictions with the field measurements. On this basis, ground vibrations generated by HSTs under different train speeds as well as the ground vibration attenuation with the distance away from the track centerline are investigated. In addition, the effects of piles and pile elastic modulus on ground vibrations are well studied. Results show that the pile-reinforcement of the subgrade could significantly contribute to the reduction of ground vibrations. In particular, the increase of elastic modulus of pile could lead to consistent reduction of ground vibrations. However, when the pile elastic modulus is beyond 10 GPa, this benefit of pile-reinforcement on vibration isolation can hardly be increased further.

Key words: high-speed railway; ground vibrations; 3D FEM; pile-supported subgrade; pile elastic modulus

Cite this article as: GAO Guang-yun, BI Jun-wei, CHEN Qing-sheng, CHEN Run-min. Analysis of ground vibrations induced by high-speed train moving on pile-supported subgrade using three-dimensional FEM [J]. Journal of Central South University, 2020, 27(8): 2455-2464. DOI: https://doi.org/10.1007/s11771-020-4461-4.

1 Introduction

The high-speed railway has been rapidly developed over the past decade all over the world for its conveniences and efficiencies. High-speed trains (HSTs) can generate the ground vibrations that travel large distance from the track center, causing discomfort to residents and misalignment of sensitive instruments, which has for years been seen as one of the major environmental problems [1, 2]. Therefore, with the rapid uptake of the high- speed railway, ground vibrations induced by HSTs have increasingly received great concerns.

Over recent two decades, various models have been developed to predict the ground vibrations generated by railways, have been applied to investigating the generation and propagation of such surface motions [1, 2]. WANG et al [3] presented a two-dimensional (2D) finite element method (FEM) model to study the vibration responses of ground due to trains’ operation. By assuming the material and geometric properties as constant along the train running direction, YANG et al [4] firstly proposed a two and a half dimensional (2.5D) FEM to study ground vibration under railway loading; BIAN et al [5] and GAO et al [6] extended this method to study HSTs induced ground vibration in varied soil medium. Despite that the 2.5D model has remarkable advantage in calculation efficiency when studying this problem, variation of soil parameters along the track direction cannot be taken into account. Therefore, CONNOLLY et al [7] developed a three-dimensional (3D) model to investigate the train induced ground vibrations considering the effect of embankment, which is capable of simulating the non-linearities at the wheel-track interface. KACIMI et al [8] studied the influence of material damping on vibration responses through a 3D train-track coupled FEM model. KOUROUSSIS et al [9] developed a high- efficiency 3D coupled finite element-infinite element model to investigate the ground vibrations generated by moving HSTs.

In the above-mentioned studies, the foundations are often simplified as homogenous elastic, visco-elastic, multi-layered or saturated media, without considering any ground reinforcements. In practice, to meet the requirements for the high- speed railway system, pile-supported subgrade has been massively used in high-speed railway construction in China due to its attractive advantages of convenient construction, small settlement and high embankment stability [10-12]. Since the piles improve the stiffness of foundation, the ground vibration responses generated by the railway with pile composite subgrade would be different from that with unreinforced foundation. While most of existing researches are limited to stability and settlement for the pile-supported embankment, studies related to the effects of pile- reinforcement on the ground vibrations are very scarce. THACH et al [13] studied the vibration behaviors of pile-supported subgrade under HSTs passage, but comparison study with the unreinforced foundation was not conducted. FU et al [14] developed a 3D FEM model and concluded that the ground improvement is effective in reducing the HSTs induced vibrations. More recently, LI et al [15] developed a 3D fully model by LS-DYNA, and studied the influences of piles on the critical speed of railway and the propagation of waves in the soils. However, these studies mainly focused on the dynamic responses of track structure, embankment or pile composite subgrade. The characteristics and attenuation of ground vibrations for such composite foundation were not discussed in detail, so do the influences of pile-reinforcement on ground vibration mitigation.

The main objective of this work is to investigate the ground vibrations of such composite foundation with pile-reinforcement subjected to moving loads induced by HSTs. 3D FEM models of pile-supported subgrade involving the pile, pile cap and cushion were established. The reliability and accuracy of the proposed numerical approach has been well validated through comparison of predictions with field measurements obtained from the Beijing-Shanghai high-speed railway. On this basis, ground vibrations generated by HSTs under different train speeds as well as the ground vibration attenuation with the distance away from track center are investigated. Additionally, the effects of piles and pile elastic modulus on ground vibrations are well studied.

2 Modelling approach and validation

2.1 Mathematical description of train loading

According to the field observations undertaken by Great British Rail Technology Center, track irregularity has been widely recognized as one of the major factors affecting the contacting force between wheels and track [16]. Vertical wheel-rail forces appear mainly in three frequency ranges: low frequency (0.5-10.0 Hz), middle frequency (30.0-60.0 Hz) and high frequency (100.0-400.0 Hz). The contacting force between wheels and track is usually controlled by the moving loads under low and middle frequency domains, while the vehicle dynamic responses are mainly dominated by the high-frequency counterpart. Thus, based on track irregularity theory, the train loading including both components of the static and dynamic load part can be expressed as follows [16]:

F(t)=P₀+P₁sin(ω₁t)+P₂sin(ω₂t)+P₃sin(ω₃t)     (1)

where P₀ denotes the static wheel load, which was set to be 75 kN (typical value for CRH380AL in China); P₁, P₂ and P₃ are the typical values of dynamic loads corresponding to ω₁, ω₂ and ω₃, which represent the low frequency, medium frequency and high frequency, respectively; P_i and ω_i (i=1, 2, 3) are given by [16]:

P_i=M₀a_iω_i², i=1, 2, 3                       (2)

ω_i=2πv/L_i, i=1, 2, 3                        (3)

where M₀ represents the unsprung mass, which was set to be 1000.00 kg; v is the train speed (km/h); L_i and a_i denote the wave length of track geometric irregularity and the corresponding vector height, respectively, the typical values of which for high-speed railway in China are as follows: L₁=10.00 m, a₁=3.50 mm, L₂=2.00 m, a₂=0.40 mm, L₃=0.50 m, a₃=0.08 mm [16].

Together with FEM software ABAQUS, the train loading is confirmed and applied by means of the DLOAD subroutine in FORTRAN code. The curve of the train loading F in the first 0.5 s at the train speed of 350.0 km/m is shown in Figure 1.

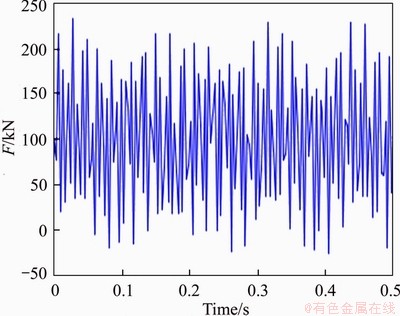
Figure 1 Curve of high-speed train moving load with speed of 350 km/h

2.2 Model development

Based on in-situ measurement performed by ZHAI et al [17] for Suzhou East Station of the Beijing-Shanghai high-speed railway, a 3D track- ground dynamic analysis model for validation involving pile and cushion was built. By taking advantage of symmetry, only one half of the finite element model was developed as shown in Figure 2 and the dimensions of which are 120 m (length)× 70 m (width)×30 m (depth). The geometry and material properties used in this verification model were consistent with Ref. [17]. The rail was modelled using Euler beam elements of 0.100 m in length, and fasteners were substituted by spring- dampers. The subgrade and pile composite foundation were modelled by applying 8 nodes solid cubic elements, and the dimensions of which were set in the range of 0.275 m to 2.500 m from near the track center to far away. A damping ratio of 0.050 was employed herein and realized with the Rayleigh damping approach [18]. In addition, to prevent the wave reflections from edges of the truncated domain, the absorbent boundaries are implemented as follows [19]:

                              (4)

                                (5)

where σ and τ denote the normal and shear stresses, respectively; a and b are the absorption parameters which are set as 1 [19]; ρ represents the density of subgrade soil; ν_p and ν_s are the longitudinal and shear wave velocities, respectively;and denote the normal and tangential velocities at boundaries, respectively.

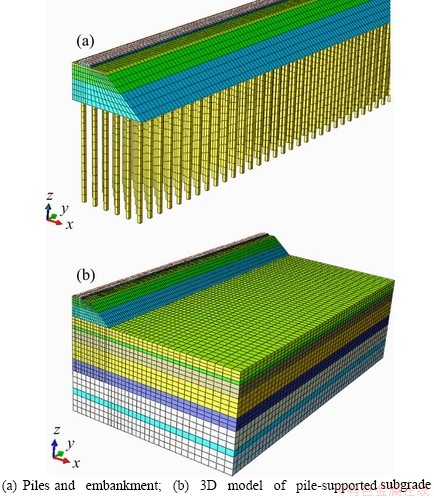
Figure 2 Finite element model for validation:

To investigate the ground vibrations of the composite foundation with pile-reinforcement as well as the effects of pile-reinforcement on the ground vibrations, a computational model involving track, embankment and pile composite foundation was developed with dimensions of 120.0 m (length)×70.0 m (width)×50.0 m (depth), as illustrated in Figure 3. To improve the calculation efficiency, the number of train carriages for the moving loads is selected to be 4.0, which has been demonstrated to be enough for simulating the multi-wheel load effect [20]. The slab track type CRTS II that is extensively used in China was selected in this model, and the parameters of which are listed in Table 1. The embankment is 3.3 m high, which consists of these three parts: 1) surface layer of subgrade, 2) bottom layer of subgrade, and 3) the rest part beneath the subgrade. The cushion is 0.6 m thick, consisting of graded broken stones and two layers of geogrid. Table 2 presents the computation parameters of the pile-supported subgrade. The corresponding profile and geotechnical parameters are in accordance with those of the typical soils distributed in the middle and lower reaching of the China’s Yangtze River. The pile selected for ground treatment is cement fly-ash gravel (CFG) pile with the following dimensions: pile length is 18.0 m; pile diameter is 0.5 m; the thickness and diameter of pile cap are 0.4 m and 1.0 m, respectively. Piles are arranged in a rectangular with center to center spacing of 1.8 m. Moreover, for the calculation case of foundation without pile, the model portions for CFG piles and pile caps were substituted by soil elements.

2.3 Validation

To verify the proposed FEM model, field data measured at Suzhou East Station of the Beijing-Shanghai high-speed railway was employed herewith [17]. Firstly, Figure 4 presents the measured and predicted time histories of vertical accelerations at 14.1 m from track center with train speed of 350.0 km/h. A cluster of vibration peak values induced by each bogie of the train can be observed in Figure 4(b), and the distributions and magnitudes agree well with those shown in Figure 4(a). That is, the ground vibrations generated by HSTs could be simulated correctly by the proposed model. To further ensure the reliability of the numerical simulation, the predicted and measured vertical peak values of ground vibration acceleration along the distance away from track center are depicted in Figure 5(a). It is observed that the predicted ground vibration responses are in good agreement with field measurements. In addition, according to a frequency-weighted method specified in ISO2631-1:1997 [21], the variations of the frequency-weighted vertical acceleration levels of ground vibrations (VL_Z) with the distance from track center for both the predicted and measured results are presented in Figure 5(b). Obviously, it is observed that the proposed model could well reproduce magnitude of the vertical acceleration level with sound accuracy, even though some slight differences are observed. It can be concluded that the proposed numerical approach is capable of simulating HSTs induced ground vibration and its attenuation process.

Figure 3 Schematic diagram of pile-supported subgrade for numerical model

Table 1 Parameters of CRTS II non-ballasted slab track

Table 2 Computation parameters of pile-supported subgrade

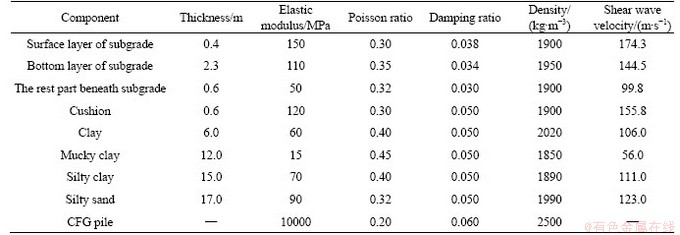
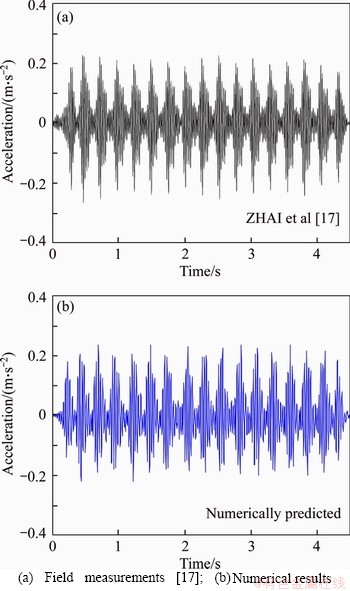
Figure 4 Time histories of ground vibration vertical accelerations at 14.1 m from track center with train speed of 350.0 km/h:

3 Results and discussions

3.1 Ground vibrations at different train speeds

Figure 6 illustrates the variations of vertical peak ground acceleration and acceleration level with train speed varying from 200 to 400 km/h. Generally, an upward trend of the peak vibration acceleration with the increase of train speed can be observed from Figure 6(a). The closer the monitoring point is to the track center, the more obvious the upward tendency is. That is, the effect of operation speed on the ground vibration is much more significant for the monitoring point that is closer to track center compared to its counterpart with further distance away from track center. In addition, as the operation speed increases, the peak values of ground acceleration increase gradually, except for the monitoring point at 10 m to the track center where the peak ground acceleration decreases slightly with the train speed increasing from 350 to 400 km/h.

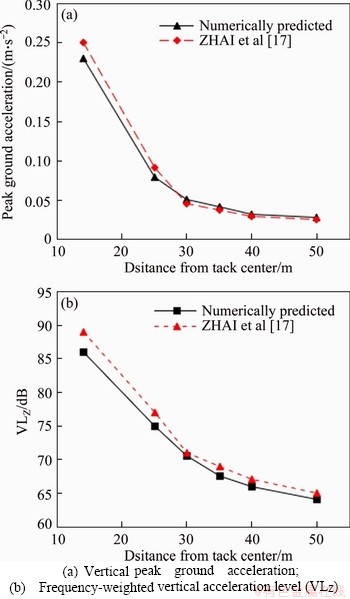
Figure 5 Variations of predicted and measured ground vibrations with distance from track center:

In Figure 6(b), the variation tendencies of the vertical acceleration level in relation with train speeds are approximately similar with those in Figure 6(a). At train speed of 350.0 km/h, the vertical acceleration level is much greater than its counterpart at 300.0 km/h. As highlighted in Ref. [22], strong ground vibration occurs when the train speed (350.0 km/h=97.2 m/s) is close to the Rayleigh wave speed (98.5 m/s) of the first soil layer that may results in the phenomenon of resonance. Moreover, the ground vibrations generated by HSTs’operation are mainly influenced by resonance in the near-track zone, but primarily dominated by train speed in the far-track zoon. Therefore, the train induced environmental vibrations could be reduced by limiting the train speed.

Figure 6 Variation of ground vibrations with train speed and distance from track center:

3.2 Variation of ground vibrations with distance to track centerline

The decay curves of vertical peak ground acceleration and acceleration level with the distance away from track center are shown in Figure 7. It can be observed from Figure 7(a) that, under five train speeds, the attenuation process of the peak values of acceleration can be approximately divided into two phases. The first phase, within the area about 30 m to the track center, could be regarded as the severe decay area in which the attenuation rates of peak acceleration are greater than 85%. The second phase called the gentle decay area is beyond 30 m away to the track center, where the decay of peak acceleration becomes clearly slow. For the vertical acceleration level, as shown in Figure 7(b), the attenuation processes could be also divided into such two phases with the dividing point of 30 m to the track center. Moreover, it indicates that strong vertical acceleration level occurs and travels further distance when the train speed reaches or exceeds the surface soil Rayleigh wave velocity.

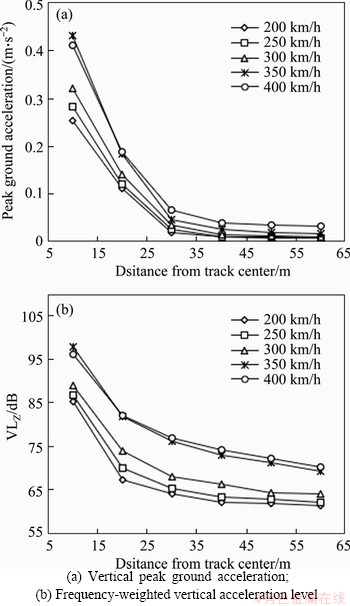
Figure 7 Ground vibration attenuation with both distance and train speed:

3.3 Ground vibration mitigation with piles

Figure 8 shows that the time histories of vertical ground acceleration at different distance from track centerline at train speed of 350 km/h. It is observed that a cluster of significant vibration peak values are induced by each bogie of train. For both the unreinforced foundation and pile-supported subgrade, the ground acceleration decays with the distance away from the track center. Nevertheless, beyond 10 m from track center, the ground acceleration without pile-reinforcement is much larger than its counterpart with the pile-supported subgrade. Moreover, the train-induced ground vibration in the pile-supported subgrade decays much more quickly compared to that in the unreinforced one. This indicates that the piles can cause a significant decrease in ground vibration and reduce the vertical acceleration effectively. Figure 9 presents the frequency spectra distribution of vertical ground acceleration within 40 m to the track center. Comparing to the foundation without piles in Figure 9(a), the spectrum amplitudes of frequency decay greatly at 10 m from track center, for both high and low frequency components. Figure 9(b) also indicates that the piles can reduce the spectrum amplitude of frequency at 40 m from track center.

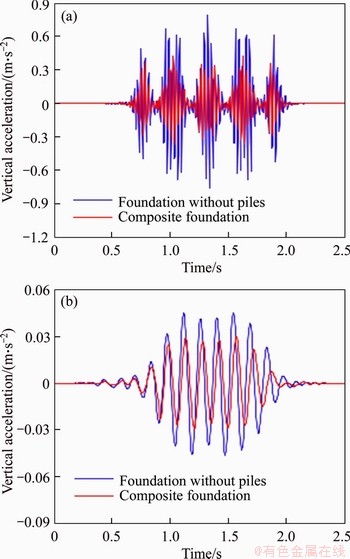
Figure 8 Time histories of vertical ground acceleration at (a) 10 m and (b) 40 m from track center at train speed of 350 km/h

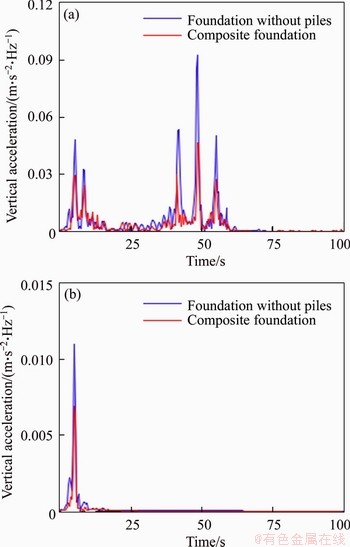
Figure 9 Frequency spectra of vertical ground acceleration at (a) 10 m and (b) 40 m from track center at train speed of 350 km/h

For illustration purpose, contour plots of the vertical acceleration magnitudes for both the unreinforced foundation and the pile-supported subgrade are depicted in Figure 10, when the train traverses the domain at the speed of 350.0 km/h. It can be observed that the piles conduct vibrations well. Compared with the case of unreinforced foundation, more vibrations could be transmitted deeper into the foundation through piles, which results in a clear reduction of the vertical acceleration along the ground away from track center. This indicates that the piles can cause a significant decrease in ground vibration and reduce the vertical acceleration effectively. Moreover, due to the train speed (350.0 km/h=97.2 m/s) is close to the Rayleigh wave speed (98.5 m/s) of the first soil layer, a typical Mach cone is formed with a series of wave fronts radiating from the loading points. And a series of trailing oscillations are also observed behind the train. Similar results, in the case of a half space subjected to a moving point load can be found in Refs. [23, 24].

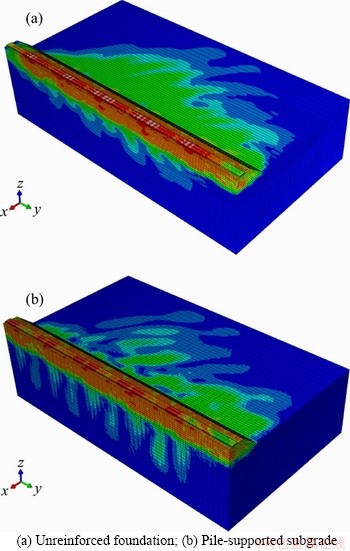
Figure 10 Contour maps of vertical acceleration for calculation models at a train speed of 350 km/h:

3.4 Vibrations of ground reinforced by piles with different pile elastic moduli

Figure 11 shows that the ground vibrations decay with the distance at the train speed of 350 km/h for the different pile elastic moduli of 1, 5, 10 and 20 GPa, and the attenuation curves for the unreinforced foundation are also given.

In Figure 11(a), comparing to the foundation without piles, the peak ground acceleration of pile-supported subgrade was reduced evidently. The impact of pile elastic modulus on the reduction of peak acceleration weakened gradually with the increasing distance from track center. Meanwhile, the peak acceleration decreases nonlinearly with the increase of pile elastic modulus. When the pile elastic modulus is beyond 10 GPa, the peak values of ground acceleration can be hardly reduced further by the increasing pile elastic modulus. As presented in Figure 11(b), the variation tendencies of vertical acceleration level with the distance from track center are similar to the peak acceleration shown in Figure 11(a). With the development of pile elastic modulus, the vertical acceleration level also decreases nonlinearly, which indicates that the train-induced ground vibrations of pile-supported subgrade could also be impacted by the other factors, like cushion, pile replacement ratio. In this work, it should be noted that the critical value of pile elastic modulus is proposed based on the analysis for the typical soils distributed in the middle and lower reaching of the China’s Yangtze River, while further validation needs to be conducted for its application for other type of soil ground conditions.

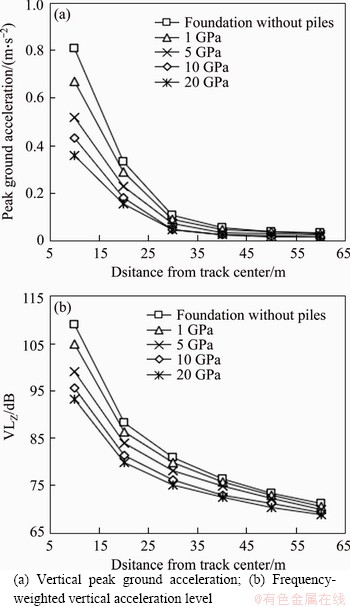
Figure 11 Variation of ground vibrations with pile modulus and distance at train speed of 350 km/m:

In addition, according to the Standard of Environmental Vibration in Urban Area (GB 10070-1988) in China [25], the vibration limit for surrounding areas along the railway line is 80.0 dB. As shown in Figure 11(b), for the composite subgrade with pile elastic modulus of 20.0 GPa, the vertical acceleration level declines to about 79.8 dB at 20.0 m away from the track centerline. However, for the unreinforced foundation, the vertical acceleration level is 80.9 dB at 30.0 m to the track center which is still greater than the criterion’s 80.0 dB.

4 Conclusions

1) The ground vibration responses exhibit an approximately upward tendency with the increase of train speed, and this influence of train speed on ground vibrations weakens gradually with the increasing distance from track center. The ground vibrations induced by HSTs moving on the pile-supported subgrade are dominated by either the resonance in the near-track zone or the train speed in the far-track zone.

2) For all train speeds, the attenuation processes of ground vibrations along the distance from track center can be divided into two phases, i.e., the severe decay phase (within 30 m away from track center), and the gentle decay phase (beyond 30 m away from track center).

3) The ground vibrations in pile-supported subgrade attenuate much more quickly compared to those in unreinforced foundation. Likewise, the spectrum amplitude decreases much more significantly than that in the foundation without treatment, for both low and high frequency components. It could be highlighted that the HSTs induced ground vibrations can be reduced evidently due to the existence of piles in the composite subgrade.

4) The increase of elastic modulus of pile could lead to consistent reduction of ground vibrations. However, this benefit of pile- reinforcement on vibration isolation can hardly be increased further as the pile modulus reaches the critical value (i.e., 10 GPa).

References

[1] CONNOLLY D P, MARECKI G P, KOUROUSSIS G, THALASSINAKIS I, WOODWARD P K. The growth of railway ground vibration problems-A review [J]. Science of the Total Environment, 2016, 568: 1276-1282. DOI: 10.1016/j.scitotenv.2015.09.101.

[2] THOMPSON D J, KOUROUSSIS G, NTOTSIOS E. Modelling, simulation and evaluation of ground vibration caused by rail vehicles [J]. Vehicle System Dynamics, 2019, 57(7): 936-983. DOI: 10.1080/00423114.2019.1602274.

[3] WANG J, ZENG Xiang-wu. Numerical simulations of vibration attenuation of high-speed train foundations with varied track bed underlayment materials [J]. Journal of Vibration and Control, 2004, 10(8): 1123-1136. DOI: 10.1177/1077546304043268.

[4] YANG Yeong-bin, HUNG Hsiao-hui, CHANG Dyi-wei. Train-induced wave propagation in layered soils using finite/infinite element simulation [J]. Soil Dynamics and Earthquake Engineering, 2003, 23(4): 263-278. DOI: 10.1016/S0267-7261(03)00003-4.

[5] BIAN Xue-cheng, CHAO Chang, JIN Wan-feng, CHEN Yun-min. A 2.5D finite element approach for predicting ground vibrations generated by vertical track irregularities [J]. Journal of Zhejiang University-Science A (Applied Physics & Engineering), 2011, 12: 885-894. DOI: 10.1631/jzus.A11GT012.

[6] GAO Guang-yun, YAO Shao-feng, YANG Jun, CHEN Juan. Investigating ground vibration induced by moving train loads on unsaturated ground using 2.5D FEM [J]. Soil Dynamics and Earthquake Engineering, 2019, 124: 72-85. DOI: 10.1016/j.soildyn.2019.05.034.

[7] CONNOLLY D P, GIANNOPOULOS A, FORDE M C. Numerical modelling of ground borne vibrations from high speed rail lines on embankments [J]. Soil Dynamics and Earthquake Engineering, 2013, 46: 13-19. DOI: 10.1016/j.soildyn.2012.12.003.

[8] KACIMI A E, WOODWARD P K, LAGHROUCHE O, MEDERO G. Time domain 3D finite element modelling of train-induced vibration at high speed [J]. Computers and Structures, 2013, 118: 66-73. DOI: 10.1016/j.compstruc. 2012.07.011.

[9] KOUROUSSIS G, PARYS L V, CONTI C, VERLINDEN O. Using three-dimensional finite element analysis in time domain to model railway-induced ground vibrations [J]. Advances in Engineering Software, 2014, 70: 63-76. DOI: 10.1016/j.advengsoft.2014.01.005.

[10] GAO Xin-jun, QIAN Hui, GUO Yuan-cheng, WANG Fei. Seismic response analysis of GRPS embankment under oblique incident P wave [J]. Journal of Central South University, 2016, 23(3): 721-728. DOI: 10.1007/s11771- 016-3117-x.

[11] ZHAO Ming-hua, HENG Shuai, ZHENG Yue. Numerical simulation on behavior of pile foundations under cyclic axial loads [J]. Journal of Central South University, 2017, 24(12): 2906-2913. DOI: 10.1007/s11771-017-3704-5.

[12] NIU Ting-ting, LIU Han-long, DING Xuan-ming, ZHENG Chang-jie. Model tests on XCC-piled embankment under dynamic train load of high-speed railways [J]. Earthquake Engineering and Engineering Vibration, 2018, 17(3): 581-594. DOI: 10.1007/s11803-018-0464-7.

[13] THACH P N, LIU Han-long, KONG Gang-qiang. Vibration analysis of pile-supported embankments under high-speed train passage [J]. Soil Dynamics and Earthquake Engineering, 2013, 55: 92-99. DOI: 10.1016/j.soildyn.2013.09.006.

[14] FU Qiang, LIU Han-long, DING Xuan-ming, ZHENG Chang-jie. Numerical investigation of piled raft foundation in mitigating embankment vibrations induced by high-speed trains [J]. Journal of Central South University, 2015, 22(11): 4434-4444. DOI: 10.1007/s11771-015-2991-y.

[15] LI Ting, SU Qian, KAEWUNRUEN S. Influences of piles on the ground vibration considering the train-track-soil dynamic interactions [J]. Computers and Geotechnics, 2020, 120: 1-12. DOI: 10.1016/j.compgeo.2020.103455.

[16] CHEN Bin, CHEN Guo-xing, SU Xiao-mei. Analysis and evaluation of ground vibration response induced by rapid rail transit [C]// LIU Han-long, DENG An, CHU Jian. Geotechnical Engineering for Disaster Mitigation and Rehabilitation. Berlin, Heidelberg: Springer, 2008: 284-293. DOI: 10.1007/978-3-540-79846-0_27.

[17] ZHAI Wan-ming, WEI Kai, SONG Xiao-lin, SHAO Ming-he. Experimental investigation into ground vibrations induced by very high speed trains on a non-ballasted track [J]. Soil Dynamics and Earthquake Engineering, 2015, 72: 24-36. DOI: 10.1016/j.soildyn.2015.02.002.

[18] SAIKIA A. Numerical study on screening of surface waves using a pair of softer backfilled trenches [J]. Soil Dynamics and Earthquake Engineering, 2014, 65: 206-213. DOI: 10.1016/j.soildyn.2014.05.012.

[19] KOUROUSSIS G, VERLINDEN O, CONTI C. Finite-dynamic model for infinite media: corrected solution of viscous boundary efficiency [J]. Journal of Engineering Mechanics-ASCE, 2011, 137(7): 509-511. DOI: 10.1061/ (ASCE)EM.1943-7889.0000250.

[20] HUNG Hsiao-hui, YANG Yeong-bin. Elastic waves in visco-elastic half-space generated by various vehicle loads [J]. Soil Dynamics and Earthquake Engineering, 2001, 21(1): 1-17. DOI: 10.1016/S0267-7261(00)00078-6.

[21] ISO 2631-1:1997. Mechanical vibration and shock— Evaluation of human exposure to whole-body vibration— Part 1: General requirements [S]. https://www.iso.org/ standard/7612.html.

[22] SHENG Xiao-zhen, JONES C J C, PETYT M. Ground vibration generated by a load moving along a railway track [J]. Journal of Sound and Vibration, 1999, 228(1): 129-156. DOI: 10.1006/jsvi.1999.2406.

[23] GALVIN P, DOMINGUEZ J. Analysis of ground motion due to moving surface loads induced by high-speed trains [J]. Engineering Analysis with Boundary Elements, 2007, 31(11): 931-941. DOI: 10.1016/j.enganabound.2007.03.003.

[24] KACIMI A E, WOODWARD P K, LAGHROUCHE O, MEDERO G. Time domain 3D finite element modelling of train-induced vibration at high speed [J]. Computers and Structures, 2013, 118: 66-73. DOI: 10.1016/j.compstruc. 2012.07.011.

[25] GB 10070-1988. Standard of environmental vibration in urban area [S]. http://openstd.samr.gov.cn/bzgk/gb/newGbIn fo?hcno=A6AC91CF7F6BA6EB6DC39E08463B06B1.(in Chinese)

(Edited by YANG Hua)

中文导读

高铁荷载下桩-土复合路基地面振动3维有限元分析

摘要：桩-土复合路基广泛应用于我国高速铁路工程建设。为研究高速列车运行引起的桩-土复合路基地面振动，本文建立了包含桩体、桩帽和垫层在内的复合路基3维有限元模型，通过与现场实测数据对比验证了模型的有效性。在此基础上，分析了不同车速高铁荷载作用下地面振动及其与轨道中心间距的衰减规律。此外，还研究了桩基及桩体弹性模量对地面振动的影响。研究表明，复合路基中桩体的加固能有效减小地面振动；另外，减振效果随着桩体弹性模量的增加而增大。然而，当桩体弹性模量超过10 GPa时，进一步增大弹性模量就不再明显增加地面振动的减振效果。

关键词：高速铁路；地面振动；3维有限元；桩-土复合路基；桩体弹性模量

Foundation item: Project(51978510) supported by the National Natural Science Foundation of China

Received date: 2019-12-04; Accepted date: 2020-05-09

Corresponding author: GAO Guang-yun, PhD, Professor; Tel: +86-21-65988575; E-mail: gaoguangyun@263.net; ORCID: https://orcid. org/0000-0001-9396-9432