J. Cent. South Univ. (2012) 19: 287-298

DOI: 10.1007/s11771-012-1003-8

Vehicle actuation based short-term traffic flow prediction model for signalized intersections

SUN Jian(孙健)¹, ZHANG Lun(张轮)²

1. Transportation Research Center, School of Naval Architecture, Ocean and Civil Engineering,

Shanghai Jiao Tong University, Shanghai 200240, China;

2. School of Transportation Engineering, Tongji University, Shanghai 201804, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: Traffic flow prediction is an important component for real-time traffic-adaptive signal control in urban arterial networks. By exploring available detector and signal controller information from neighboring intersections, a dynamic data-driven flow prediction model was developed. The model consists of two prediction components based on the signal states (red or green) for each movement at an upstream intersection. The characteristics of each signal state were carefully examined and the corresponding travel time from the upstream intersection to the approach in question at the downstream intersection was predicted. With an online turning proportion estimation method, along with the predicted travel times, the anticipated vehicle arrivals can be forecasted at the downstream intersection. The model performance was tested at a set of two signalized intersections located in the city of Gainesville, Florida, USA, using the CORSIM microscopic simulation package. Analysis results show that the model agrees well with empirical arrival data measured at 10 s intervals within an acceptable range of 10%-20%, and show a normal distribution. It is reasonably believed that the model has potential applicability for use in truly proactive real-time traffic adaptive signal control systems.

Key words: adaptive signal control; least-squared estimation; microscopic simulation; travel flow prediction; urban arterials

1 Introduction

An advantage of utilizing an adaptive traffic signal controller is the ability to vary cycle length, phase splits, and even the phase sequence from cycle to cycle, so that the immediate traffic demand pattern can be efficiently handled. To provide the needed functionality, the controller must make use of a set of on-line optimized phasing and timing parameters. Previously adaptive control systems, such as SCOOT [1], make incremental adjustments to the current signal plan in response to changing traffic patterns in order to facilitate traffic flow. With SCATS [2], the local intersection controller chooses the timing parameters on the basis of the degree of saturation and then incrementally adjusts the timings to accommodate varying traffic conditions. The major drawback of these systems is that they are reactive and not proactive in nature, and consequently unable to anticipate changes in traffic flow. RHODES, yet another real-time traffic-adaptive signal control system, uses a traffic flow arrival algorithm called PREDICT [3-4] to improve the effectiveness of online phase timing calculations. In the PREDICT algorithm, detector information from the approaches of every upstream intersection, along with signal state information (red or green), phasing and timing, and queue length, is used to predict anticipated vehicle arrivals. However, the PREDICT algorithm was only tested using a network of fixed-time upstream traffic signals, and was not tested with either actuated or traffic-adaptive signals.

CAREY et al [5] modeled the “whole link” travel time for a vehicle entering a link as a function of the time and the average flow rate in the vicinity of the vehicle, treating the travel time as a function of the number of vehicles on the link. This model performs well in a theoretical environment, particularly for the dynamic traffic assignment (DTA), where the length of the link is not large, and vehicles are assumed uniform distributed. However, in the empirical situation, the number and location of detectors are limited, and consequently, is almost impossible to obtain the real time average flow rate for each link segment. ZHENG et al [6] proposed a real-time adaptive control model that can be applied to an existing traffic actuated control system. In the model, available signal-timing data, such as the max-out/gap-out information, parameter settings, and phase split were used to describe the current and expected traffic conditions. Optimal control parameters were determined on the basis of these descriptions and provide signal- timing data for further optimizations. However, the focus this adaptive control model was placed on the basic control parameters provided by modern actuated controllers. The turning proportions of the upstream intersections were not incorporated appropriately, and thus the vehicle arrival pattern and the corresponding dispersion factors of the studied intersection were not modeled. Close examination of the existing traffic adaptive systems reveals that one common disadvantage is their failure to utilize available detector, timing and phasing information. Consequently, their applicability was confined to particular traffic situations and the performance on a comprehensive basis was often less than desirable one. As a signalized intersection generally offers a wealth of information, such as detector actuations, signal timings (including minimum green, vehicle extension, maximum green, etc), and signal phasing, they are useful in predicting arrivals at a downstream intersection. In this work, a traffic flow prediction model was presented based on actuated upstream intersections, trying to make full use of the information to predict anticipated arrivals at a downstream intersection. To validate the accuracy of the model, traffic counts were taken on the approach and compared to the volumes predicted. Two components, a travel time prediction model and a turn proportion estimation model were proposed for the traffic flow prediction model.

2 Travel time prediction model for upstream vehicle actuation

2.1 Assumptions and definitions

Traffic contributing to the arrivals at d_A emanates from the three approaches of intersection B, which can be measured by detectors d_l, d_t, d_r (see Fig. 1(a)), respectively. By defining each vehicle actuation on any upstream detector (d_l, d_t, d_r) as an event, the left-turn event actuated at d_l would pass d_A and contribute to the approach volume at downstream intersection A. The same logic applies to the right-turn and through events from d_r and d_t. The left-turn, through and right-turn proportions for the three approaches are determined individually, and can be generalized as a vehicle crossing a detector i (i∈{l, t, r}). Assuming intersection B adopts the standard eight-phase control logic, as shown in   Fig. 1(b), the event at detector d_l can occur during any of two signal states (red or green, the yellow and all-red times are considered as effective green time). Hence, the prediction model can be divided into two components based on the corresponding signal state, a green phase model and a red phase model.

2.2 Travel time prediction for vehicle actuation during green phase

Within actuated signal timings, the green time for each phase can be divided into intervals as shown in  Fig. 2. Any vehicle arrival occurring during the green phase must fall into one of three time intervals:    or  where  is the start time for green phase of current cycle at intersection B;  is the initial green interval which intents to provide sufficient time clear all vehicles potentially stored between the detector i and the stop bar at intersection B, equal to G_min-U (G_min is the minimum green time, and U is the unit or vehicle extension/gap time); is the maximum time period from the beginning of current green phase during which a vehicle could possibly pass intersection B without signal delay, otherwise when the vehicle arrives at stop bar, the signal will change to red, equal to G_max-U (G_max is the maximum green time).

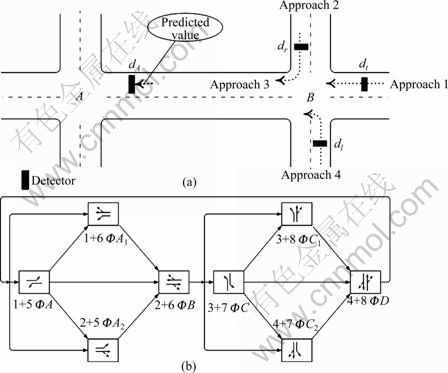
Fig. 1 Geometric layout and phase information for objective intersection: (a) Geometric layout for arrival prediction; (b) Standard eight-phase diagram for actuated signal controller in intersection B

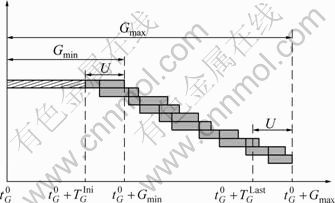
Fig. 2 Time intervals along green phase horizon

1) If a vehicle arrival occurs during the green phase and before  (see Fig. 3(a)), the vehicle can pass through intersection B even if no unit extension (U) is appended. The arrival time at d_A was estimated as

       (1)

where  is the time that the vehicle crossing detector i in intersection B arrives at detector A;  is the time that the event of any vehicle crossing detector i is trigged, i?{l, t, r};  is the travel time from d_i to the stop bar at intersection B;  is the travel time from intersection B to the detector d_A.

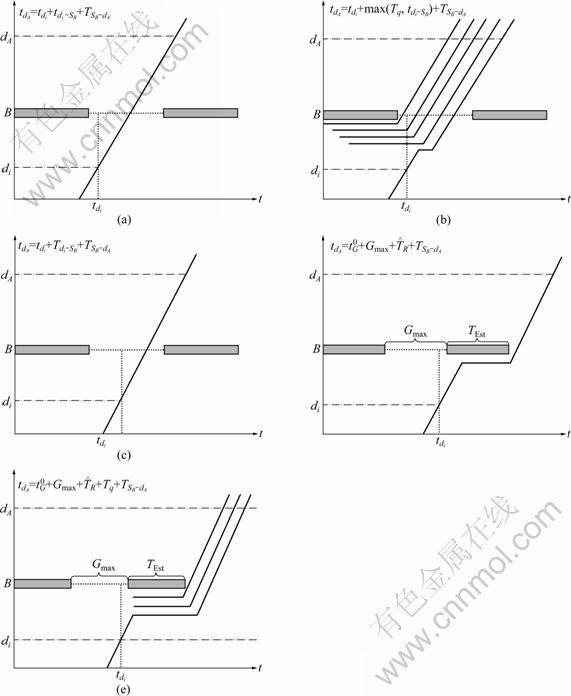
Fig. 3 Delays associated with green-time actuation predict model: (a) MinGreen Triggered Event without delay  (b) MinGreen Triggered Event with queue delay  (c) Extension Green Triggered Event without delay  (d) MinGreen Triggered Event with signal delay (e) MinGreen Triggered Event with signal dely and queue delay

2) If the vehicle arrives before  but with a standing queue (see Fig. 3(b)), the arrival time at d_A is estimated as

                                            (2)

where T_q is the delay due to the remaining queue discharge (at intersection B).

HEAD [4] compared the number of vehicles in the queue based on estimation/prediction filter with a simple counting estimator and found that a simple counting estimator provides reasonably accurate information. Therefore, a simple counting estimator is used to estimate T_q as a₀+a₁*N (a₀ and a₁ are parameters calibrated from field data).

3) Figure 3(c) depicts the case wherein a vehicle arrives at a time between  and  and a unit extension was appended to the current movement, which ensures that the vehicle passes intersection B during the current green phase. The travel time is defined as

                               (3)

Standing queue is unlikely existed on such occasion, since the initial green interval  would clear all vehicles stored between the detector and the stop line.

4) When a vehicle arrival occurs after time   (see Fig. 3(d)), the green time will end after  G_max because of the “maxing-out”. The detected vehicle has to wait until the next green phase to pass and the predicted time is

               (4)

where T_Est is the estimated duration of the red phase followed. A detailed estimation for this value was provided in Section 2.3.

5) Similarly, when vehicles arrive after  and a queue exists, as shown in Fig. 3(e), the delay time T_q is added in, and the total predicted time changes to

                               (5)

As shown in Figs. 3(d) and 3(e), the arrived vehicle must wait until the next green phase because of the “maxing-out”. Hence a detailed estimation of the beginning of next green time, as provided in Section 2.3, needs to be carried. Additionally, estimating the start of next green (or end of the other actuated phases) would enable us to explore events triggered during the red phase inclusively, and then scenarios for actuated control could be treated similarly to those of pre-timed one.

2.3 Travel time prediction for vehicle actuation during red phase

The green phase actuation model predicted the travel time for vehicles passing an advance detector during the green time. However, if a vehicle arrival was actuated in red signal, it must stop and wait until the following green phase, except in certain extreme situations, e.g. when the vehicle arrives at the stop bar, the current phase is changing from red to green. To predict the travel time under red phase, an estimation of the time duration from the event triggered point to the end of the current red phase should be conducted. Since the shorter time interval estimation generally provides higher credible results, only the remaining red time from the triggering point is estimated instead of the total red duration.

From the perspective of an actuated signal controller, the red time for the current movement occurs simultaneously with the green time for other movements (yellow and all-red intervals are included into effective green time). Consequently, the estimation can be divided into a continuum of green time over the movements composed of the phase ring diagram. Assuming that intersection B adopts a standard eight-phase controller, the ring diagram in a time horizon, together with the green and red time related to the through event triggered in d_l are depicted in Fig. 4. The total red time is equal to

(T_y is the

the summation of the yellow and all red intervals). The corresponding vehicle actuation time and estimation intervals are provided in Table 1.

Using the following equation, we can approximate the green time interval for ΦA, ΦA+ΦA₂ (or ΦA₁), ΦB, ΦC, and ΦC+ΦC₂ (or ΦC₁) in current cycle from the last three signal cycles and splits:

(6)

where μ₁, μ₂ and μ₃ are on-line adjustment coefficients, which are modified dynamically based on the linear combination of the corresponding phase duration in last n cycles (n≥6). The generalized least-square error (GLS) method is used to estimate values of μ₁, μ₂ and μ₃, and n is the intersection related parameter, which could be calibrated from field dataset or multi-runs of simulation. During the numeric examples, n is chosen as 6 to simplify the procedure, and the initial difference between actual and predicted values is set as 0 (e.g.,  Consequently,

(i=1, 2, 3, …, n-3)                                         (7)

Fig. 4 Ring diagram and time intervals divided in red-phase

Table 1 Relationship between arrival red time and intervals need to be estimated

As the red phase duration is determined, the period can be divided into two intervals:  and . As shown in lower part of Fig. 4, four different scenarios of red-time triggered event as Figs. 5(a)-(d) could occur, where  is the begin time instance for red phase of current cycle at intersection B;  is the estimated period for the red phase of current cycle;  is the maximum time period from the beginning of current red phase during which a vehicle would stop by current red signal, otherwise when the vehicle arrives at stop base, the signal will change to green and let it pass, equal to

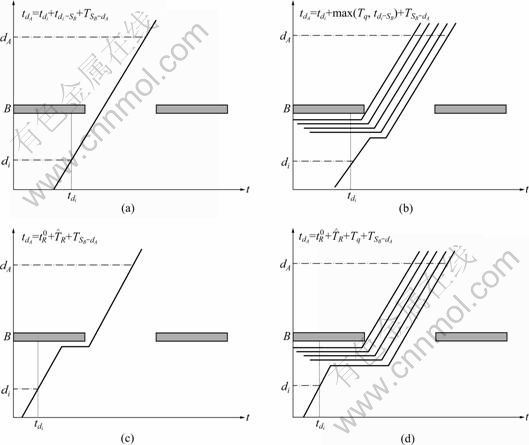
Fig. 5 Delays associated with red-time actuation predict model: (a) Red-time Triggered Event without delay   (b) Red-time Triggered Event with queue delay  (c) Red-time Triggered Event with signal delay  (d) Red-time Triggered Event with signal delay and queue delay

1) If a vehicle arrival event is triggered in a red phase but, when it arrives at stop bar, the current phase is changed from red to green (), the vehicle can pass through intersection B without stopping (see Fig. 5(a)). The arrival time at d_A is estimated as

(8)

2) Figure 5(b) shows the same scenario as Fig. 5(a), except that a standing queue is now presented. In this case, the queue delay time T_q should be considered and the arrival time at d_A is estimated as

                                   (9)

3) and 4) When a vehicle arrival occurs before time , as shown in Figs. 5(c) and 5(d), whether or not a queue exists, it must wait until next green phase.

Without a standing queue, the travel time is defined as

           (10)

With a standing queue, the travel time is defined as

   (11)

3 On-line method to estimate dynamic turning proportions

In addition to the number of vehicles actuated at d_i and the queues related, the turning proportions at upstream intersection B are also essential to predict the downstream flow at detector d_A. The prediction models need consider the probability that each vehicle passing any upstream detector (d_l, d_t, d_r) travels along the route BA and arrives at downtown intersection A. In PREDICT algorithm [3], this uncertainty was quantified by introducing probability p_i^BA when computing the expected number of arrivals at d_A at future time t_p= t_da for movement i at detector d_i. However, how to obtain an exact p_i^BA value was not provided during the rest of examples and experiments. An assumption is made that pre-estimation for turning proportions at the intersection has been carried out.

3.1 Overview of turn proportion estimation

Turn proportion estimation has been broadly explored in the literature and many models have been proposed [7-10]. The majority of models required counts for one cycle, plus prior turning proportion estimation [7]. The accuracy of these methods is highly dependent on how well the prior estimates match the actual turning proportions. On the other hand, time-series methods do not need prior estimates but require a long time frame, which impedes their responsiveness. These estimates become highly inaccurate during times of sudden and highly irregular turning movement changes caused by unforeseen events, such as traffic accidents. Unfortunately, during such unforeseen events, responsiveness is exactly needed most by the traffic signal system. Another method for estimating intersection turning movement proportions from less than complete sets of traffic counts was proposed by DAVIS and LAN [8]. In their method, both entering and exiting traffic counts at each intersection approach were used. The method even works under certain conditions where the number or placement of detectors does not support complete counting. However, the method is largely restricted to certain geographic scenarios and, if the detector configuration does not satisfy an identified condition, it fails to work. CHANG and TAO [9] gave a time-dependent turning estimation for signalized intersections in which, by including the approximate intersection delays, the model can account for the impacts of signal setting on the dynamic distribution of intersection flows. Furthermore, in this method, to improve the estimation accuracy, pre-estimated turning factions from a relatively long time interval should serve as additional constraints. Furthermore, in Nobe’s dissertation [10], four closed-form estimations were developed, two of which 1) maximum entropy (ME) and 2) generalized least-squared (GLS) need prior turning proportion estimates. The rest are 3) least-squared error (LS) and 4) least-squared error/generalized least-squared error (LS/GLS), which require counts from three previous cycles. Despite several layouts were considered, the four models were applied to intersections with a fixed two-phase cycle (North-South phase and East-West phase), with each phase including two protected right-turn. This is different from NEMA control strategy, wherein right-turns are always set as permitted mode as minor movements. In the four models, two types of counts, cycle counts and phase counts, were considered separately for the estimation purpose. In fact, a combination of these two counts can bring more efficiency under some scenarios. Given that the entering vehicle lane counts and exiting vehicle counts during every traffic signal phase and in each direction of an intersection are generally available, a simple estimation of turning proportions, relying only on short-term vehicle counts, was proposed for the NEMA eight-phase signalized intersection as in the remainder of this section.

3.2 Model for turning proportion estimation

Taking Phase 1 of a NEMA-controlled intersection as an example, Fig. 6(a) presents all corresponding movements. Considering the phase-based exiting vehicle counts and cycle-based entering volumes during the previous cycle (=k-1), the notations for the analysis of the turning proportion model include 1)  The number of vehicles that entered the intersection from direction i during previous cycle (=k-1); 2)  The number of vehicles that left the intersection to direction i during phase l of previous cycle (=k-1); 3)  The estimated number of vehicles that traveled from i to j during phase l of previous cycle (=k-1); 4)  The estimated turning proportion of vehicles that traveled from i to j in current cycle (=k), where i=E, W, N, S; j=E, W, N, S; l=1, 2, 3, 4, 5, 6, 7, 8.

Only the traffic from NORTH link was examined,

as vehicles from other directions can be developed by rotating the notation by 90?, 180? or 270?, respectively. The given conditions related to movements from NORTH link during the cycle k-1 include

                                                (12)

                          (13)

                            (14)

                                (15)

                    (16)

                     (17)

                     (18)

                           (19)

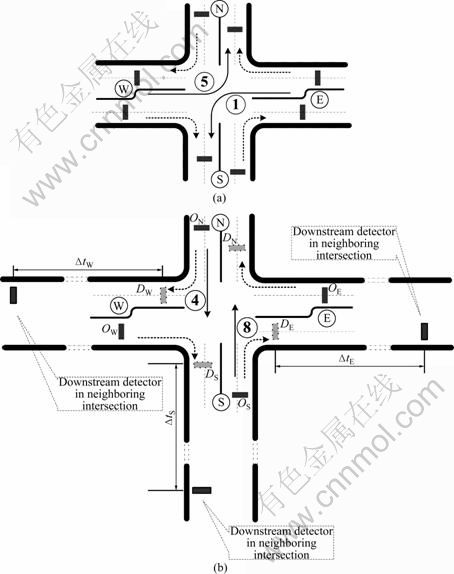
Fig. 6 Typical movements included and volume measurement for each phase in intersection B (8-phase NEMA controller is adopted): (a) Phase 1: movement 1 and 5 (taking Phase 1 for example, movements for other phases can be deduced); (b) Measurement of entry and outbound vehicle counts for given phase (taking Phase 8 for example)

The total right-turn volume during cycle k-1 consists of the volume in each phase. Four of them,    and  can be measured directly. Suppose that all right-turn movements in the given cycle k-1 are in a continuum uniform pattern (this only means that the right turn volume in the same cycle is in a continuum uniform pattern, but it cannot be applied to different cycles). The right-turn volumes within the rest of phases can be estimated as

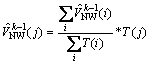                             (20)

where T(l) is the time period duration for each phase l, i=1, 2, 6, 8, and j=3, 4, 5, 7.

Using Eq. (20), along with the rest right-turn volumes, such as    and , the other two types of vehicle movements (left turn and through) can be obtained by using Eqs. (16)- (19). Then, the total volumes for left-turn, through and right-turn were calculated by summing the vehicles in corresponding phases, and consequently the turning proportion can be calculated as

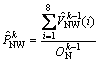                               (21)

                                      (22)

                         (23)

Since the total proportion equals one, the three turning proportions are balanced as

                      (24)

                      (25)

                         (26)

In the estimation model, exit passage detectors and signal status are needed for the vehicle counts process, so that the exit volumes for each phase can be obtained correctly. However, most current urban intersections do not implement exit detectors except in some regions of California, US [10]. To estimate the exit flow for each phase, the available downstream detectors in neighboring intersection were used with consideration on the distance in between. The counts from the downstream detectors in each phase were corrected using the travel time from the subject intersection to the downstream detectors. This travel time can be estimated on the basis of the approach and link flow speed. Assuming the travel time from the current intersection to the corresponding downstream detectors in the neighbor intersections to be Δt_W, Δt_S and Δt_E, as shown in Fig. 6(b), during cycle k-1, if each phase i begins at time instance t_i, the exiting vehicles to the other three links in Eqs. (12)-(19) can be counted as

               (27)

                     (28)

                        (29)

where O_U(t_i, t_j) (U=W, E or S), is the number of vehicle counted on the downstream detectors in the corresponding neighbor intersections during the time period [t_i, t_j].

4 Numerical examples

4.1 Comparison of observed travel times and predicted travel times

The proposed travel time prediction model was implemented using a computer simulation based on CORSIM 6.0. An additional simulation plug-in was developed to record the previous and current signal states [11-12], so that the travel time for each objective vehicle was estimated. The simulated network was based on an actual network in Gainesville, Florida, US, which consisted of 34 zones and 13 intersections. Although the prediction and control algorithms were applied to a single intersection, it was necessary to simulate the area surrounding the intersection of interest to ensure a realistic traffic flows [13]. To provide a desirable environment, it was assumed that no traffic sources or sinks existed between the links connecting the intersections.

The geometric scenario for collecting the results data is shown in Fig. 1(a). The primary signalized node A and one of the satellite signal node B are located       1 070.5 ft (326.3 m) apart. The three upstream detectors, d_l, d_t, d_r, are located 155 ft (47.2 m), 150 ft (45.7 m) and 152 ft (46.3 m) from node B, while d_A is located 240 ft (73.1 m) upstream of intersection A. The simulation was run for 75 min, of which the first 15 min were used for initialization. According to the three types of upstream movements (left turn, through and right turn) and two prediction models (green phase and red phase), the prediction model was tested by following five scenarios as: 1) NBL vehicles (left-turn) of Green Phase Actuation, 2) NBL vehicles (left-turn) of Red Phase Actuation, 3) WBT (through) vehicles of Green Phase Actuation, 4) WBT (through) vehicles of Red Phase Actuation and 5) SBR vehicles (right-turn) of Green Phase Actuation. No right-turn vehicles have red time, since all right-turns were set as permitted movements.

Figures 7(a)-(e) show a plot of actual versus predicted travel time for vehicles traveling from upstream detector d_i to downstream detector d_A under each scenario. The perfect prediction line for each plot should be along the line y=x, which is also the general trend for the plot points. Most of the scatters in the plots are due to natural stochastic variation in travel times, except two significant errors. First, the actual travel time is long but the predicted travel time is short, especially for the green phase prediction component (for both through and left turn movements). This may be due to the fact that some phases end before a vehicle crosses the stop bar, but the prediction model expects the vehicle to be clear the intersection, which causes that the predict travel time is shorter than the actual travel one. The other error is that the actual travel time is short and the predicted time is long if a vehicle passes through the intersection (B) but the prediction model expects it to stop. However, most errors in the prediction are in an acceptable range of 10%-20% and show a normal distribution (see Figs. 7(a)-(e)), corresponding to white noise rather than a systematic error [14].

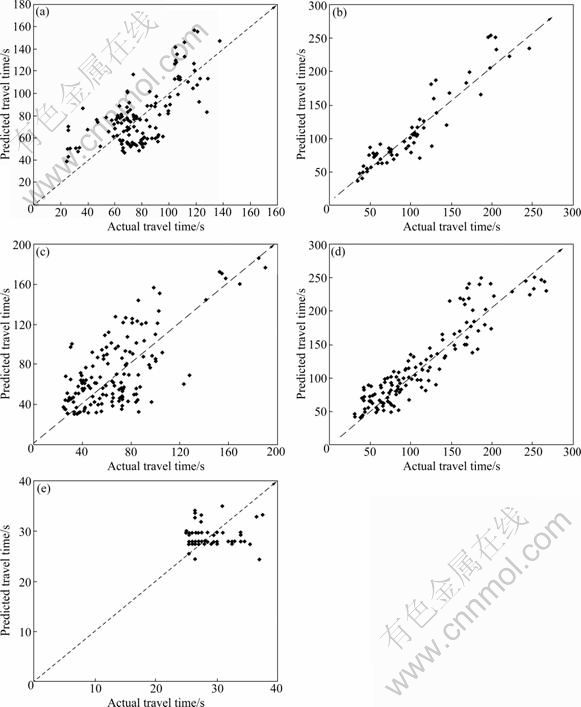
Fig. 7 Actual versus predicted travel time plots: (a) For left-turn event triggered during green phase; (b) For left-turn event triggered during red phase; (c) For through event triggered during green phase; (d) For through event triggered during red phase; (e) For right-turn event

4.2 Comparison of actual and predicted flow arriving at downstream detector d_A

4.2.1 Test results with predefined turning ratios in downstream intersection B

To characterize the prediction model better, Fig. 8 exhibits the actual and predicted flow profile arrival at d_A as a function of time. The x-axis represents time and is divided into 10 s time interval. The y-axis represents the cumulative number of vehicles arriving during each 10 s time interval. It is generally accepted that a congested intersection desires a policy with a switching frequency that is no less than 10 s. Since the total simulation time is 4 500 s and the first 900 s is used for initialization, only the results for two periods of simulation time: 1 000-   2 000 s and 3 000-4 000 s, are shown. The turning ratios in the three upstream detectors are provided as input parameters (d_l=0.25, d_t=0.9 and d_r=0.1), which are determined offline from the Synchro model based on historical data.

From Figs. 8(a) and (b), it can be inferred that the actual flow profile matches the predicted flow profile.

4.2.2 Test results with estimated turning ratios in downstream intersection B

In addition to the historical data based fixed turning proportions which were provided as given parameters (based on historical data), the online turning proportion estimation method, as introduced in Section 3, was also tested and the simulation results were compared with the results from the historical based model. By adapting the estimation model instead of the historical based fixed turning ratios, an actual and predicted flow profile arrival at d_A can be obtained, as shown in Fig. 9. Similar to the results exhibited in Fig. 8, the time series (x-axis) is divided into 10 s time intervals and the y-axis represents the cumulative number of vehicles arriving during each 10 s time interval. As before, two periods of results,    1 000-2 000 s and 3 000-4 000 s, are presented.

From the plots in Fig. 9, it is inferred that the predicted flow profile matches the actual one better than the flow profile in Fig. 8, which supports the applicability of the on-line turning proportion estimation procedure.

4.2.3 Results evaluation

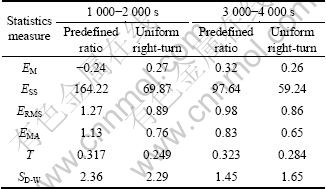
The performance of the prediction model with two different turning proportion scenarios (one uses predefined turning ratios as input parameters, and the other takes the right turning movements in upstream intersection as periodic uniform flow) can be assessed numerically by some linear statistics. Standard measures between actual traffic flow and predicted vehicles include Mean Error (E_M), Sum of the Squared Errors (E_SS), Mean Squared Error (E_MS), Root Mean-Square Error (E_RMS), and Mean Absolute Error (E_MA), etc [13], are defined in Eqs. (30)-(33):

                                           (30)

                             (31)

                   (32)

                        (33)

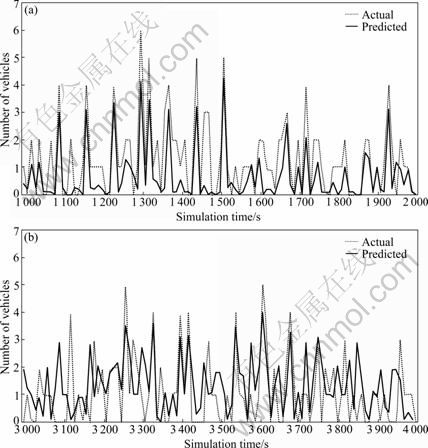
Fig. 8 Flow profiles showing actual and predicted number of arrivals for model with fixed turning ratios: (a) Simulation period from  1 000 s to 2 000 s; (b) Simulation period from 3 000 s to 4 000 s

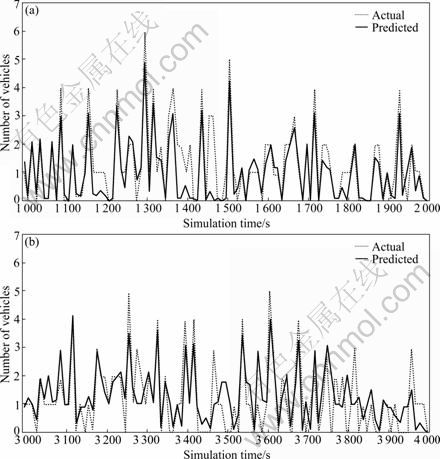
Fig. 9 Flow profiles showing actual and predicted number of arrivals for model with estimated turning ratios: (a) Simulation period from 1 000 s to 2 000 s; (b) Simulation period from 3 000 s to 4 000 s

Table 2 provides the measures for the flow profile generated by simulation experiments in Fig. 8 and Fig. 9. Theil’s inequality coefficient (T), as listed in Eq. (34), was used as a measure of prediction accuracy in case of intervals without any observed arrivals. Durbin-Watson (S_D-W) statistic, as listed in Eq. (35), was also provided to measure the existence of any pattern in the prediction errors (if S_D-W is close to 2, the errors are essentially random). For this study, given that both the Theil’s inequality coefficients are smaller than 1, and the D-W statistic values are close to 2, we can conclude that the errors are essentially random, which consequently verifies the effectiveness of the proposed model:

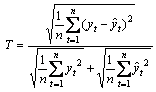                      (34)

where 0≤T≤1, T→0 predicts that the model is good, T→1 predicts that model is not good.

                            (35)

where

Table 2 Descriptive statistics of predicted traffic arrival process

5 Conclusions

1) By exploring available detector and signal controller information from neighboring intersections, a dynamic data-driven flow prediction model was developed. The model consists of two prediction components based on the signal states (red or green) for each movement at an upstream intersection. Using a set of turning proportion estimation techniques at the upstream intersection, along with the predicted travel times, anticipated vehicle arrivals are forecasted at the downstream intersection. However, one of the issues by using loop detector data is the accuracy problem, caused by the dysfunction of the equipment. It is recommended that additional sources, such as AVL data or GPS data, are included to supplement the research.

2) The arrival prediction model can be further tested by incorporating it into an existing online adaptive traffic control system (such as Rhodes) and, through simulation, identifying the resulting reduction in vehicular delay. Hardware-in-the-loop simulation can then be used to investigate all of the controller’s capabilities, instead of the limited subset of standard features supported by standard simulation programs, which would further provide opportunities to investigate the advanced features of adaptive signal control, such as signal coordination and signal preemption strategies.

3) A more sophisticated on-line look-ahead optimization algorithm, such as a decision tree model, would allow us to dynamically adjust signal timing and phasing at any intersections of interest. Following the optimization of a single intersection, additional future research would focus on entire networks of intersections. Using small/kernel network harmonization, any intersection can be combined together with adjacent intersections to form a composite intersection, for which an optimum control strategy can be computed. By continuing to add adjacent intersections to the composite intersection, eventually a global optimum will be achieved. The end result would be a globally optimum set of signal timings and phasing which can minimize the overall vehicular delay.

References

[1] Robertson D I, Bretherton R D. Optimizing networks of traffic signals in real time–the SCOOT method [J]. IEEE Transaction on Vehicular Technology, 1991, 40(1): 11-15.

[2] Lowrie P R. SCATS: A traffic responsive method of controlling urban traffic control [R]. Roads and Traffic Authority, 1992.

[3] Head K L. Event-based short-term traffic flow prediction model [J]. Transportation Research Record, 1995, 1510: 45-52.

[4] MIRCHANDANI P M, WANG F Y. RHODES to intelligent transportation systems [J]. IEEE Intelligent Systems, 2005, 20(1): 10-15.

[5] CAREY M, GE Ying-en, MCCARTNEY M. A whole-link travel-time model with desirable properties [J]. Transportation Science, 2003, 37(1): 89-96.

[6] ZHENG Xing, RECKER W, CHU Lian-yu. Optimization of control parameters for adaptive traffic-actuated signal control [J]. Journal of Intelligent Transportation Systems, 2010, 14(2): 95-108.

[7] Maher M J. Estimating the turning flows at a junction: A comparison of three models [J]. Traffic Engineering and Control, 1984, 25: 19-22.

[8] Davis G A, LAN C J. Estimating intersection turning movement proportions from less-than-complete sets of traffic counts [J]. Transportation Research Record, 1995, 1510: 53-59.

[9] Chang G L, Tao X. Estimation of time-dependent turning fractions at signalized intersections [J]. Transportation Research Record, 1997, 1644: 142-149.

[10] Nobe S. On-line estimation of traffic split parameters based on lane counts [D]. The University of Arizona, 1997.

[11] SUN Daniel(Jian), Kondyli A. Modeling vehicle interactions during lane changes on arterial streets [J]. Computer-Aid Civil and Infrastructure Engineering, 2010, 25(8): 557-571.

[12] SUN Daniel(Jian), Elefteriadou L. Research and implementation of lane-changing model based on driver behavior [J]. Transportation Research Record, 2010, 2161: 1-10.

[13] Porche I, Lafortune S. Adaptive look-ahead optimization of traffic signals [J]. Journal of Intelligent Transportation Systems, 1999, 4(3/4): 209-254.

[14] LIU Tian-liang, HUANG Hai-jun, TIAN Li-jun. Microscopic simulation of multi-lane traffic under dynamic tolling and information feedback [J]. Journal of Central South University: Science and Technology (English Edition), 2009, 16(5): 865-870.

[15] Makridakis S, Wheelwright S C, McGee V E. Forecasting: Methods and applications [M]. New York: John Wiley and Sons, 1998: 43-54.

(Edited by YANG Bing)

Foundation item: Project(71101109) supported by the National Natural Science Foundation of China

Received date: 2010-10-27; Accepted date: 2011-05-06

Corresponding author: ZHANG Lun, Associate professor, PhD; Tel: +86-21-69583695; E-mail: Lun-zhang@tongji.edu.cn