基于SVM的“弹性系数-投入产出”电力需求预测分析模型

董力通^1,2，谭显东³，刘伟国⁴，刘海波^1,2

(1．华北电力大学 经济与管理学院，北京，102206；

2．国网北京经济技术研究院，北京，100052；

3．国网能源研究院，北京，100052；4．国家电网公司，北京，100031)

摘要：基于合理预测电力需求，是保证电网规划与产业发展合理性的重要依据，在我国优化产业结构、推进节能减排的环境下，电力中长期需求的变化面临更多不确定因素，考虑多个因素对电力经济发展弹性系数的影响，按照投入产出模型，运用支持向量机算法构建预测模型。以2000—2009年我国电力需求及GDP，产业结构的数据为样本，预测2010年的电力需求总量。通过与普通弹性系数回归预测、普通支持向量机预测方法对比，电力需求总量预测精度分别提高8.90%和3.98 %。

关键词：电力需求；弹性系数；投入产出；支持向量机

中图分类号：F426          文献标志码：A         文章编号：1672-7207(2012)06-2441-04

Model of forecasting and analysis electricity demand based on SVM of elastic coefficient and input-output

DONG Li-tong^1,2, TAN Xian-dong³, LIU Wei-guo⁴, LIU Hai-bo^1,2

(1. School of Economics and Management, North China Electric Power University, Beijing 102206, China;

2. State Power Economic Research Institute, Beijing 100052, China;

3. State Grid Energy Research Institute, Beijing 100052, China;

4. State Grid Corporation of China, Beijing 100031, China)

Abstract: Based on the fact that the demand of electricity must be reasonably forecast, which is an important basis to ensure the power grid planning and industrial development, in order to optimize industrial structure and promote energy conservation and emission reduction, there are many uncertain factors to change the medium and long-term electricity demand, considering the effects of multiple factors on the elastic coefficient of the electric power economic development, according to the input-output model, a forecasting model was constructed using the algorithm of support vector machine(SVM). Using electricity demand and GDP, taking the industrial structure of data in 2000—2009 as samples, the total electricity demand in 2010 was forecast. The results show that compared with elastic coefficient regression forecasting and ordinary common SVM forecasting method, the forecasting accuracy of the total electricity demand increases by 8.90% and 3.98%, respectively.

Key words: electricity demand; elastic coefficient; input-output; support vector machine(SVM)

合理预测电力需求对于制定电力规划、电力建设具有重要意义。当前，国内外有关电力需求方面的研究较多，主要包括电力需求的预测方法^[1-6]、电力需求预测应考虑的因素^[7-8]等。程鹏等^[9-10]将并联灰色神经网络模型与GM(1,1)模型进行了改进，并将其应用于电力需求预测中。Amusaa等^[11]使用边界检验的方法研究了南非的电力需求。郭彦东等^[12-13]研究了基于支持向量机的电力需求预测方法。这些方法都较好地拟合了数据样本的趋势性规律和特征，但是，对于一些关键影响因素变化对需求影响未充分考虑。特别是没有从能源与经济相互关系出发建模，并没有运用数据挖掘和预测算法进行综合研究。为此，本文作者首先提出影响电力需求的主要因素，并研究各因素对电力需求所产生的影响；其次，结合弹性系数和投入产出模型，构建考虑我国节能减排、产业结构、经济布局调整等因素的改进模型，以2000—2009年产业结构、经济总量、能源消费总量为样本，通过对2010年能源消费总量的预测，并将分析结果与在相同条件下运用普通弹性系数回归方法和SVM回归预测方法所得结果进行比较，验证改进后模型的分析精度。

1  影响电力需求的主要因素分析

电力需求的变化主要由经济结构和能源消费方式的改变决定。在国家高度重视可持续发展的背景下，中长期电力需求增长主要受产业机构调整、经济布局调整、节能减排(低碳经济)发展共3个方面的影响。

(1) 产业结构调整。我国政府高度重视产业结构调整工作，提出通过优化产业结构，降低经济发展对能源及其他自然资源的消耗强度。通过对高耗能产业实施限制性政策，引导和鼓励新兴、绿色产业的发展。由于自身能耗水平不一致，产业结构的变化将对总体电力需求造成较大的影响。

(2) 经济布局调整。未来华东、华中、西北地区产业的跨区域转移和优化升级将成为经济增长的新的内生动力，在未来区域板块的合作发展中逐步完成产业结构调整。随着各区域规划的逐步落实，相关地区的经济发展将带动电力需求的增长，也将推进我国各地区经济、电力协调发展。

(3) 低碳经济发展。2009年我国提出了2020年二氧化碳排放比2005年下降40%~45%的目标。从能源供应来看，可优化能源供应结构；从需求供应来看，通过节能减排、技术进步以及高效用电设备的利用，提高能源利用效率。这些变化将对我国能源需求总量、能源消费结构、电力需求结构和电力消费结构产生较大的影响。可通过限制高耗能行业的发展、加大节能减排措施的实施力度、大力发展清洁能源、促进资源的循环利用与建立低碳技术创新体系等途径实现节能减排目标。这些方法措施的实施，从能源供应侧角度，优化了能源供应结构；从需求侧角度，通过节能减排、技术进步以及高效用电设备的利用，可提高能源利用效率。

2  电力需求预测模型

2.1  弹性系数模型

弹性是经济学中重要的概念。弹性系数是一定时期内相互联系的2个指标增长速度的比率，它是衡量一个变量的增长幅度对另一个变量增长幅度的依存关系。弹性系数法在对一个因素发展变化预测的基础上，通过弹性系数对另一个因素的发展变化作出预测的一种间接预测方法。设x为自变量，y为x的可微函数，则y对x的弹性系数定义为： (其中，导数为瞬间变化率或边际变化，为平均变化率)。则弹性系数是变量y的瞬间变化率与平均变化率   之比。

2.2  电力需求弹性投出产出模型

电力弹性系数反映了一定时期内电量需求与国民经济增长速度之间的内在关系，是电力系统中长期预测中一种非常经典的方法。电力弹性系数大于1，表明电力需求的增长速度高于国民经济的增长速度。若相邻2 a的国内生产总值分别用和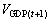表示，相应2 a的电力需求用E_t和E_t+1 表示，则GDP的增长速度为：

       (1)

用电量的增长速度为：

          (2)

电力弹性系数为：

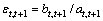            (3)

已知历史时段1＜t≤n的电力弹性系数序列，并已知未来年份GDP的增长率，首先按照电力弹性系数变化的特征，运用相应的方法预测未来年份的电力弹性系数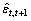，则可以基年的电量E_n为基础，预测未来各年的电量需求：

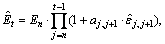 t≥n+1   (4)

2.3  基于SVM的电力弹性系数投入产出需求预测 模型

将全社会用电量分为各产业用电量和居民生活用电量，产业用电量分为第一产业用量、第二产业用量与第三产业用电量。利用投入产出模型(IO)进行中长期电力需求预测，即根据未来的经济增长状况确定各部门的电力需求。利用此模型体现了以需定产的市场经济思想，即以需求为导向，生产满足需求，可以清楚地描述电力需求的构成，具有很好的可解释性。本文建立基于SVM的电力弹性系数投入产出需求预测模型，求解未来的电力需求。

将全社会用电量Y分为第一产业用电量Y₁、第二产业用电量Y₂、第三产业用电量Y₃和居民用电量Y_e，即

            (5)

利用投入产出模型的思想，结合情景分析技术，构建改进的中长期电力需求预测。在式(1)，(2)和(3)基础上，通过细分第一、二、三产业电力弹性系数，采用SVM对历史数据中第一、二、三产业结构变化对电力需求影响的模拟，构建预测模型。通过设定误差率和学习次数，控制SVM模拟过程。

            (6)

其中：r为误差率；Y′为预测用电量；Y为实际用电量。

3  模型校验与比较

以2000—2009年我国第一、二、三产业GDP，第一、二、三产业及社会居民用电量以及总用电量为样本，通过计算各年一、二、三产业电力需求量作为输入，预测2010年电力需求总量。将本文提出的改进模型与普通电力弹性系数预测方法(方法一)、普通SVM回归预测(方法二)进行比较，以验证本文提出算法的改进效果。

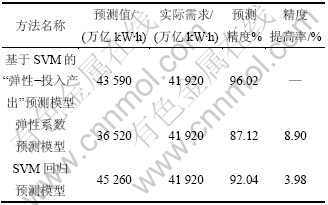
不同方法预测效果的比较结果(基于对2010年电力消费总量的预测)如表1所示。从表1可见：与方法一、方法二相比，运用本文提出方法所得结果预测精度分别提高8.90%和3.98%，这从一定程度上佐证了本文提出方法能够更全面地反映影响中长期电力需求的内在规律，能够获得更好的分析和预测用电量。

表1  不同方法预测效果的比较(基于对2010年电力消费总量的预测结果)

Table 1  Comparison of forecast effects for different methods

4  “十二五”电力需求预测与分析

本文考虑“十二五”期间不同GDP增长率下2015年的用电需求情况，假定第一、第二和第三产业GDP增长率分别为9.6%，8.7%和7.0%。假定2010年全国GDP总量为302 523亿元，第一、第二和第三产业结构GDP总量比为10.1:48.4:41.5。三种情景下具体各产业的GDP总量 如下。

情景1：预计“十二五”期间年均增长9.6%，2015年全国GDP总量将达到47.8万亿元，第一、第二、第三产业结构GDP总量比为8.7:48.9:42.5。

情景2：考虑国家经济布局调整，预计“十二五”期间年均增长8.7%，2015年将达到45.9万亿元，第一、第二、第三产业结构GDP总量比为8.9:47.8:43.3。

情景3：考虑低碳经济发展、能源消费总量控制，预计“十二五”期间年均增长7%，2015年将达到43.6万亿元，第一、第二、第三产业结构GDP总量比为9.3:46.9:43.8。如表2所示^[14]。

表2  3种情景下2015年的GDP总量

Table 2  GDP of three situations in 2015   亿元

以2010年为基准年，第一产业、第二产业、第三产业对电力的直接消耗系数分别为40.81，5.95和38.14，居民生活用电支出为2 562.5亿元。2015年，第一产业、第二产业、第三产业对电力的直接消耗系数分别为42.12，6.78和39.11，居民生活用电支出为3 626.5亿元。应用投入产出模型的结果如表3所示。

在情景1中，GDP年均增长率较快，主要是第二产业的用电量较大，第三产业发展较快，至2015年全社会用电量预计为82 536亿kW·h；在情景2中，GDP年均增长率适当，至2015年全社会用电量预计为   76 050亿kW·h；在情景3中，GDP年均增长率缓慢，至2015年全社会用电量预计为70 019亿kW·h。

表3  应用基于SVM的改进弹性-投入产出模型2015年电力需求总量预测结果

Table 2  Forecast results of electricity demand in 2015 using improved input-output model based on SVM  亿kW·h

5  结论

(1) 根据弹性系数方法和投入产出分析模型的思想，利用SVM回归方法利用SVM回归方法在有限样本情况下的求解结果具有较高的准确性，构建能够反映中长期需求多重重要影响因素的分析预测模型。

(2) 通过实证分析，将本文构建的预测模型与弹性系数方法和SVM回归预测方法在对统一问题预测时进行验证比较，发现采用本文提出的方法所得电力需求总量预测精度分别提高8.90%和3.89%。

(3) 运用SVM的输出结果，通过设定不同的GDP增长情况和第一、二、三产业结构变化结果，通过对能源消费总量控制、产业结构变化、经济布局等因素的情景设定，对2015年我国电力需求变化进行了预测，这对政府制定较准确的电网规划具有一定的借鉴意义。

参考文献：

[1] 唐平雅. 电力需求预测方法和能源需求预测模型探讨[J]. 中国电力, 2000, 33(4): 32-34.
TANG Ping-ya. Research on power demand forecasting method and energy demand forecasting model[J]. Electric Power, 2000, 33(4): 32-34.

[2] 顾洁, 储琳琳, 施伟国. 不确定性中长期电力需求预测方法探讨[J]. 电力需求侧管理, 2010, 12(3): 10-13.
GU Jie, CHU Lin-lin, SHI Wei-guo. Study on uncertainty mid-longterm power demand forecasting method[J]. Power Demand Side Management, 2010, 12(3): 10-13.

[3] 徐言, 陈丽萍, 周晖, 等. 基于港口经济特点分析的电力需求预测[J]. 电力学报, 2009, 24(3): 178-183.
XU Yan, CHEN Li-ping, ZHOU Hui, et al. Electricity demand forecasts based on the analysis of the port economy[J]. Journal of Electric Power, 2009, 24(3): 178-183.

[4] Dilaver Z, Hunt L C. Industrial electricity demand for Turkey: A structural time series analysis[J]. Energy Economics, 2011, 33(3): 426-436.

[5] 秦康平. 节能减排背景下电力需求预测方法的研究[D]. 上海: 上海交通大学信息与电气工程学院, 2010: 5-20.
QIN Kang-ping. Methods of electric load forecasting based on energy-saving and emission reduction[D]. Shanghai: Shanghai Jiaotong University. School of Electronic and Electrical Engineering, 2010: 5-20.

[6] Erdogdu E. Electricity demand analysis using cointegration and ARIMA modelling: A case study of Turkey[J]. Energy Policy, 2007, 35(2): 1129-1146.

[7] 黄晨宏. 影响上海电力需求的主要因素及电力需求预测[J]. 电力需求侧管理, 2011, 13(3): 71-76.
HUANG Chen-hong. Main factors affecting Shanghai electric power demand and its forecasting[J]. Power Demand Side Management, 2011, 13(3): 71-76.

[8] Psiloglou B E, Giannakopoulos C, Majithia S, et al. Factors affecting electricity demand in Athens, Greece and London, UK: A comparative assessment[J]. Energy, 2009, 34(11): 1855-1863.

[9] 程鹏, 韦雅君, 李金颖, 等. 基于改进的并联灰色神经网络模型在电力需求预测中的应用[J]. 广东电力, 2011, 24(8): 13-16.
CHENG Peng, WEI Ya-jun, LI Jin-ying, et al. Application of improved model of parallel grey neural networks in power demand forecast[J]. Guangdong Electric Power, 2011, 24(8): 13-16.

[10] 李明洋, 田利强, 张希亮. 改进型GM(1,1)模型在电力需求预测中的应用[J]. 山西建筑, 2011, 37(4): 126-127.
LI Ming-yang, TIAN Li-qiang, ZHANG Xi-liang. On application of an improved GM(1,1) model in electricity demand forecasting[J]. Shanxi Architecture, 2011, 37(4): 126-127.

[11] Amusaa H, Amusa K, Mabugu R. Aggregate demand for electricity in South Africa: An analysis using the bounds testing approach to cointegration[J]. Energy Policy, 2009, 37(10): 4167-4175.

[12] 郭彦东, 李荣. 基于支持向量回归的年电力需求预测方法[J]. 控制理论与应用, 2008, 27(6): 6-8.
GUO Yan-dong, LI Rong. Annual electric demand forecasting based on support vector regression[J]. Control Theory and Applications, 2008, 27(6): 6-8.

[13] 从荣刚, 张燕琳, 赵亚楠. 基于SVM模型的山东省电力需求预测[J]. 能源技术经济, 2011, 23(3): 40-45.
CONG Rong-gang, ZHANG Yan-lin, ZHAO Yan-an. Prediction of Shandong power demands based on the SVM model[J]. Energy Technology and Economics, 2011, 23(3): 40-45.

[14] 李鑫, 朱龙飞, 邓淇中. 我国三次产业结构演进与宏观经济波动分析[J]. 湖南科技大学学报: 社会科学版, 2012, 15(3): 65-69.
LI Xin, ZHU Long-fei, DENG Qi-zhong. An analysis of three industrial structure’s evolutions and macroeconomic fluctuations in China[J]. Journal of Hunan University of Science & Technology: Social Edition, 2012, 15(3): 65-69.

(编辑 陈灿华)

收稿日期：2011-07-15；修回日期：2011-09-16

基金项目：教育部新世纪人才基金资助项目(NCET-060208)

通信作者：董力通(1979-)，男，吉林长春人，博士研究生，工程师，从事电力经济、电力市场等领域研究工作；电话：010-63411717；E-mail：hoffman_d@163.com