J. Cent. South Univ. (2017) 24: 699-707

DOI: 10.1007/s11771-017-3471-3

Elastoplastic modeling of mechanical behavior of weak sandstone at different time scales

WANG Jing-yin(王京印)¹, ZHANG Yu(张玉)^{2, 3}, JIA Yun(贾赟)³, JIN Pei-jie(金培杰)², ZHU Li-hong(朱丽红)¹

1. School of Petroleum Engineering, China University of Petroleum, Qingdao 266555, China;

2. College of Pipeline and Civil Engineering, China University of Petroleum, Qingdao 266555, China;

3. Laboratory of Mechanics of Lille, University of Lille 1, Villeneuve d’Ascq 59655, France

Central South University Press and Springer-Verlag Berlin Heidelberg 2017

Abstract: A unified constitutive model is proposed to describe the mechanical behavior of weak sandstone at different time scales. The instantaneous behavior of this material is characterized by the Drucker-Prager elastoplastic model, while the time-dependent deformation is described in terms of the microstructure evolution. This evolution is numerically simulated by progressive degradation of the elastic modulus and failure strength of the material. The proposed model is used to simulate the instantaneous triaxial compression and the multi-loading creep tests. Generally, good concordance is obtained between numerical simulations and experimental data. The proposed model is capable of describing the main features of these rocks, particularly irreversible deformations, pressure dependency, volumetric transition between compaction and dilatancy, and creep behavior.

Key words: weak sandstone; elastoplasticity; creep behavior; constitutive model; microstructure

1 Introduction

The time-dependent behavior of rock is basic mechanical properties of the rock material, which can be considered an important base in explaining and analyzing the phenomena of geological tectonic movement, as well as predicting the long-term stability for rock engineering. A previous laboratory investigation reported that both instantaneous and time-dependent irreversible deformations had been observed in weak sandstones [1-4]. In the framework of long-term stability analysis of hydraulic engineering, considering the time-dependent responses of this rock is necessary [5-9]. And due to the ubiquity of creep behavior of rock, it is greatly important and urgent to study such mechanical properties and to produce a relational expression of constitutive model [10-12].

In the classic modes, two separate constitutive models are adopted to describe the instantaneous plastic responses caused by applied stress variation and the creep plastic behavior caused by the material viscosity effect [13-15]. Generally, a mathematical description of creep behavior is provided by these models [16-18]. However, the physical mechanisms of creep behavior have not been investigated and proposing an accurate constitutive model with the simulation and the prediction is still difficulty and hotpot on research of rock time scales theory. Therefore, it is crucial to understand the time-dependent behavior by means of both laboratory tests and numerical methods.

Experimental investigation on time-dependent behaviors of rock under the various confining pressures is an important foundation for proposing constitutive model. The experimental results obtained in the previous study show that the development of creep behavior in weak sandstones is mainly associated with the progressive evolution of the microstructure, such as the subcritical propagation of microcracks. Moreover, numerous consistent experimental results can be found in Refs.[19-23]. Thus, some constitutive models have been proposed to describe the time-dependent behavior of sandstones [16, 20, 24-28]. In these models, time-dependent inelastic behavior is generally described by visco-plastic theory and a large number of parameters have to be determined.

PIETRUSZCZAK et al [29, 30] have proposed a general methodology for the description of creep in terms of microstructural evolution. SHAO et al [31, 32] have used this methodology to propose a unified model for the description of short-term and long-term responses of an argillaceous rock. However, this model involves eleven parameters and only can be used to describe the plastic failure surface of quadratic function. Based on those previous researches, an improved Drucker-Prager elastoplastic constitutive model is proposed in this study to describe the instantaneous and time-dependent behavior of weak sandstones. The constitutive model for the time-dependent behavior is logically formulated from the extension of the model for instantaneous behavior. Time-dependent deformation is considered a macroscopic consequence of the progressive degradation of the material structure.

2 Elastoplastic model at different time scales

2.1 Elastoplastic model for time-dependent behavior

Weak sandstones are assumed to exhibit irreversible deformations in different time scales: instantaneous plastic strain 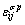because of stress evolution and time- dependent creep strain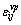because of microstructural evolution. Therefore, the total strain is expressed as

                   (1)

The general form of the stress-strain relation is written as

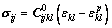                          (2)

where 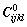is the initial elastic-stiffness tensor component. Instantaneous damage is assumed neglected because the emphasis of the present study is on the description of the time-dependent behavior of weak sandstones. Meanwhile, an internal variable ζ is introduced to provide a quantitative description of the microstructure evolution. This variable is expressed as a scalar valued function of the plastic strain and evolves with time. In addition, for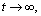 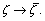Therefore, 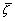represents a stationary state associated with the microstructure equilibrium at the grain contact level that depends on the confining pressure and deviatoric stress. The kinetics of microstructure evolution can be described in terms of the deviation from the equilibrium state, measured by 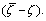To simplify, the evolution law may be expressed in a simple linear form as

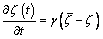                            (3)

where γ is a material constant;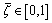while 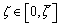. Function ζ(t) can be formally defined by using the Laplace transforms and convolution theorems. Taking ζ(0)=0, we obtain:

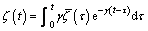                     (4)

Thus, degradation parameter ζ depends on the history of the time derivative of while the exponential term represents the memory effect. The elastoplastic behavior of a representative volume of material should be affected by ζ because parameter ζ represents the relative change in the cemented contact area of grains in this material [20]. Inspired by the research work in Ref. [31], we assume that time-dependent degradation affects the elastic modulus as follows:

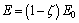                               (5)

where E₀ is the initial elastic modulus of the weak sandstone. According to the plasticity mechanism, following the framework developed in Refs. [29, 30] and considering the time-dependent degradation effects, the plastic yield criterion and the plastic potential can be respectively expressed in the following general forms:

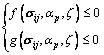                            (6)

In these equations, σ_ij represents the Cauchy stress tensor; α_p is the plastic-hardening function and can be deduced by the standard derivative of the thermodynamic potential. By introducing the degradation of elastic modules into constitutive Eq. (2), we can write the incremental form of the constitutive equation as

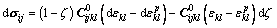  (7)

The plastic strain can be defined using the plastic flow rule as

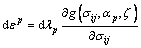                      (8)

The plastic multiplier dλ_p is determined by introducing Eq. (7) into the plastic consistency condition in the following form:

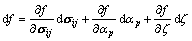              (9)

Thus, we have

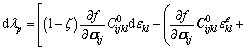
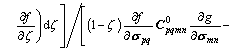
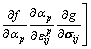                      (10)

The plastic flow can be decomposed into two parts: the instantaneous plastic strain caused by the strain variation dε_kl created by the applied deviatoric stress and the plastic creep strain caused by material degradation dζ. By introducing Eqs. (10) and (8) into constitutive Eq. (7), we obtain the increment of stresses for a prescribed increment of strains as follows:

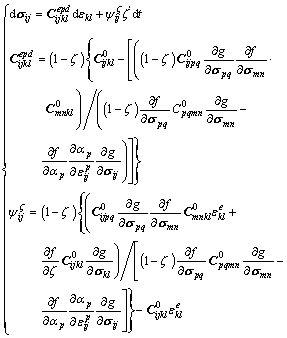 (11)

where 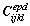is the tangent elastoplastic stiffness tensor of the damaged material and corresponds to the instantaneous variation of stresses caused by applied stress variation; 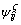is the second-order tensor that defines the variation of stress during relation process induced by material degradation. In the absence of material degradation (ζ=0 and dζ=0), is the fourth-order tangent elastoplastic tensor, and the instantaneous plastic behavior is characterized by the basic plastic model. Equation (11) can be easily implemented in a computer code with the finite element method [18] and the displacements of nodes as principal unknowns.

2.2 Application to creep behavior

In the creep test case, the material is subject to a given stress level. Therefore, determining the variation of strains as a function of time is necessary. The stress- strain relation is first obtained by investing Eq, (7) as follows:

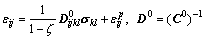           (12)

where D⁰ is the initial elastic compliance tensor of the intact material in drained condition. By using the differentiation of the previous equation, we can obtain the increment form of the strain-stress relation as follows:

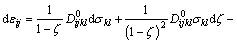
           (13)

We can rewrite the strain–stress relation Eq. (13) in the following form:

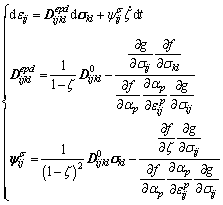         (14)

where 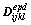is the tangent elastic compliance tensor of the damaged material and is the second-order tensor that defines the creep behavior. Therefore, creep strain can be evaluated as a function of material degradation.

3 Specific elastoplastic model for weak sandstones

3.1 Determination of specific functions

As a continued study, the physical properties and mechanical behavior of weak sandstone have been performed on previous study [33, 34]. Based on the microstructure analysis of the typical weak sandstone, the mineralogical compositions mainly included quartz, feldspar, sericite, chlorite, and a small amount of iron. Moreover, the rock had loose organizational structure, medium porosity and high moisture content. The cementation was porous cement, and the rock belonged to highly weathered sandstone with poor physical and mechanical properties. Typical stress-strain curves from triaxial compression tests have shown that large plastic strains are observed in the axial and lateral directions after the deviatoric stress loading. Moreover, material strength, plastic flow, and creep evolution depend strongly on the mean stress. Therefore, a Drucker-Prager type of linear function is adopted to describe the plastic yielding and failure surface as follows (Fig. 1):

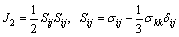           (15)

where p is the mean stress and q is the deviatoric stress.Parameter C₀ represents the material cohesion, while A is the frictional angle of the failure surface. Microstructure evolution also induces material strength degradation and has an effect on the plastic behavior of weak sandstones. Similar to linear function Eq. (5), the time-dependent degradation effect on the evolution of failure surface parameter A is described by the following function:

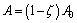                               (16)

where A₀ is the frictional angle of the failure surface for intact material. In an instantaneous triaxial test, where ζ=0 and dζ=0, the effects of parameters C₀ and A₀ on the failure surface are shown in Figs. 2 and 3, respectively.

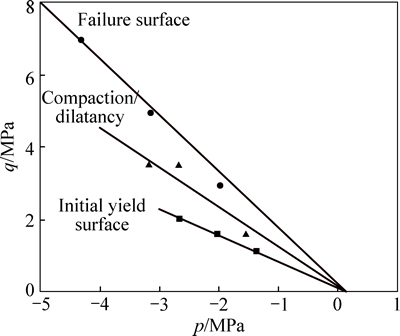
Fig. 1 Illustration of plastic yielding surface, failure surface and compaction/dilatation boundary in p-q plan for weak sandstone

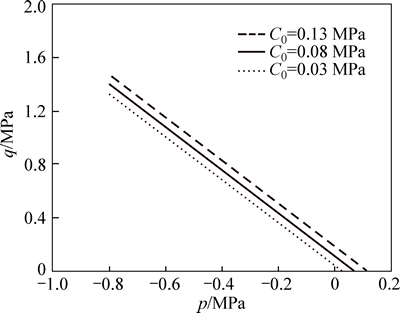
Fig. 2 Influence of cohesion parameter C₀ on failure surface

Plastic hardening is described by the increasing function α_p of the generalized plastic shear strain γ_p. The following exponential function is proposed for the plastic-hardening law:

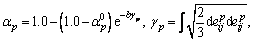
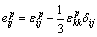                      (17)

Fig. 3 Influence of frictional coefficient A₀ on failure surface

The initial value of yield function defines the initial plastic yield threshold and can be deduced by drawing the locus of stresses at the onset of the inelastic strains (see Fig. 1). The ultimate value of the hardening function is α_p=1, which corresponds to the material failure. Parameter b controls the hardening law rate. The yield surface evolution with the plastic hardening process is illustrated in Fig. 4.

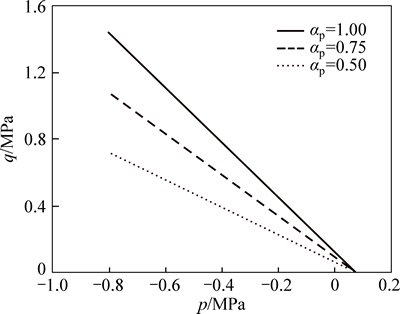
Fig. 4 Evolution of yield surface with plastic hardening function α_p

Furthermore, the volumetric strain of weak sandstones exhibits a dramatic transition from compaction to dilatancy [33]. In view of this, proposing a non-associated plastic flow rule is necessary. Inspired by the elastoplastic model proposed by [32], we use the following function:

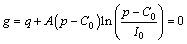              (18)

Variable I₀ represents the stress state at the intersection between the plastic potential surface and the mean stress axis p-C₀, and its value is negative (I₀<0). On the basis of this potential, the stress space is divided into two zones that respectively correspond to plastic compressibility and dilation. The boundary between these two zones is defined by the condition 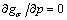(see Fig. 1).

3.2 Identification of model parameters

The proposed model contains seven parameters: two elastic constants for the intact material (E₀, v₀), four parameters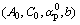for the description of instantaneous plastic behavior, and one parameter (γ) for the time-dependent behavior.

The initial elastic constants (E₀, v₀) can be observed from the linear part of the stress-strain curves from the triaxial compression tests. The mean values obtained in various triaxial compression tests are used in the numerical simulation because only a very slight variation of elastic parameters is observed with the confining pressure.

The four parameters 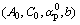that control the evolution of instantaneous plastic behavior can be identified by using a series of triaxial compression tests performed under different confining pressures. The parameters included in the failure criterion (A₀, C₀), which characterize the failure surface, can be deduced by drawing the locus of peak stresses in the p-q plane. The parameter for the initial yield surface 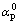is captured from the locus of stresses at the onset of inelastic strains. Plastic-hardening parameter B can be obtained by drawing the function of α_p versus the plastic deviatoric strain γ_p (Fig. 5).

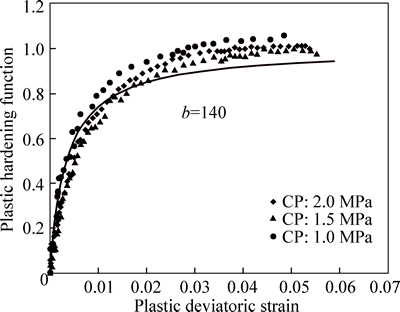
Fig. 5 Evolution of plastic hardening function α_p versus plastic deviatoric strain γ_p (CP: Confining pressure)

The parameters related to the time-dependent responses can be determined by simulating a creep test. Therefore, all the parameters of the proposed model are identified using a creep test and a series of triaxial compression tests performed under different confining pressures [33, 34], and their values are summarized in Table 1.

Table 1 Typical values of model parameters for weak sandstone

3.3 Parametric study

Aforementioned, the parameters of proposed model can be identified from relevant experimental data. In order to get a good knowledge on the performance of proposed model, the influence of model’s parameters on mechanical behavior of weak stone are studied. The values given in Table 1 are taken as the reference ones. When the influence of one parameter is studied, we change only the value of this parameter but leave the others alone. Two tests are simulated with different series of parameters, which include:1) A instantaneous triaxial tests performed under the confining pressure of 2.0 MPa; 2) A creep test conducted with the confining pressure of 2.0 MPa and the deviatoric stress 5.00 MPa.

The influence of the elastic modulus E₀ is firstly studied (Figs. 6 and 7). The comparison of numerical results shows that deformations increase significantly when E₀ decreases. This phenomenon is due to the fact that the deformability of the rock increases when the E₀ decreases. However, the peak stress has not been disturbed by the variation of E₀. The same tendency is observed in the numerical simulation of creep test. The creep strains increase significantly with the decrease of E₀.

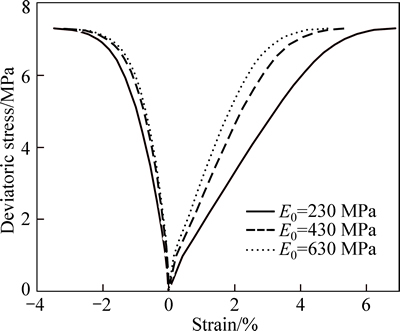
Fig. 6 Influence of elastic parameter E₀ on strain-stress curves

Fig. 7 Influence of elastic parameter E₀ on creep strain

In the proposed model, the kinetics of hardening law is controlled by the parameter b. According to the Eq. (17), α_p increases significantly when the value of B is great (Figs. 8 and 9). The yield surface of studied material attains rapidly the failure surface. For a given level of stress, a small strain is then observed in the case where b=190 while important deformation develops in the material when b=90. By using Eq. (17), the influence of confining pressure on the kinetic of hardening law is taken into account by using the function χ_p. Therefore, the proposed model is capable to describe the dramatic transition from brittle to ductile behavior observed in the triaxial compression tests. On the other hand, the same tendency is observed in the creep tests.

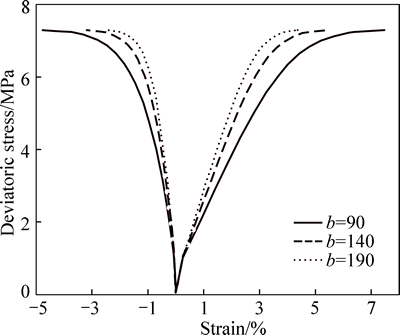
Fig. 8 Influences of b on strain-stress curves

Fig. 9 Influences of b on creep strain

4 Numerical simulations of laboratory tests

4.1 Instantaneous elastoplastic behavior

The instantaneous triaxial compression test simulations are presented in Fig. 10. Generally, good agreement is obtained between the simulation results and experimental data [33]. Moreover, the dependence of mechanical behavior on the confining pressure is well-simulated. In conclusion, the proposed model is able to reproduce the instantaneous behavior of weak sandstones under triaxial loading conditions. The following comparisons represent a verification of the consistency of parameters because these tests have been adopted to determine the model parameters.

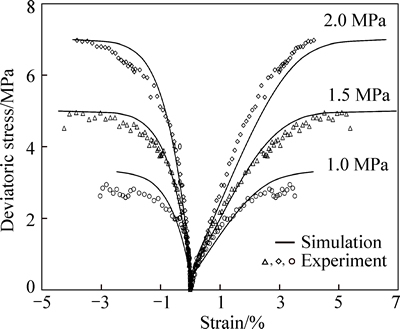
Fig. 10 Simulation of triaxial compression tests under different confining pressures

4.2 Time-dependent behavior

The proposed model is now applied to simulate creep tests performed on weak sandstones with different confining pressures (Fig. 11). During the tests, deviatoric stress is applied with multi-loading steps until the macroscopic failure of the samples. The proposed model can correctly describe the creep behavior of weak sandstones during different multi-loading steps. Using the proposed model, we can predict the diminution of elastic modulus with time as a macroscopic consequence of microstructural evolution (Fig. 12). In general, elastic modulus decreases progressively over time and elastic modulus degradation decelerates with the increase of the confining pressure. Moreover, the value of 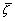increases by a logarithmic function with the deviatoric stress growth during multi-loading creep tests (Fig. 13). By comparing the curves obtained with different confining pressures, the confining pressure is observed to prevent the development of microstructure degradation. The smallest 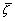is obtained when the confining pressure is 2.0 MPa.

4.3 Difference between instantaneous strain and time- dependent strain

Based on the simulation results, the total strain of weak sandstone can be divided into two parts: an instantaneous elastoplastic strain due to applied load and a time-dependent plastic strain during creep process induced by material degradation (Fig. 14). Confining pressure has a great impact on the instantaneous and time-dependent strain. At low confining pressure, the time-dependent strain is larger than instantaneous strain, while the time-dependent strain is smaller than instantaneous strain at relative high confining pressure. It is indicated that the instantaneous strain increases and the time-dependent strain decreases with the increase of confining pressure. Therefore, the confining pressure can delay the creep behavior of weak sandstone.

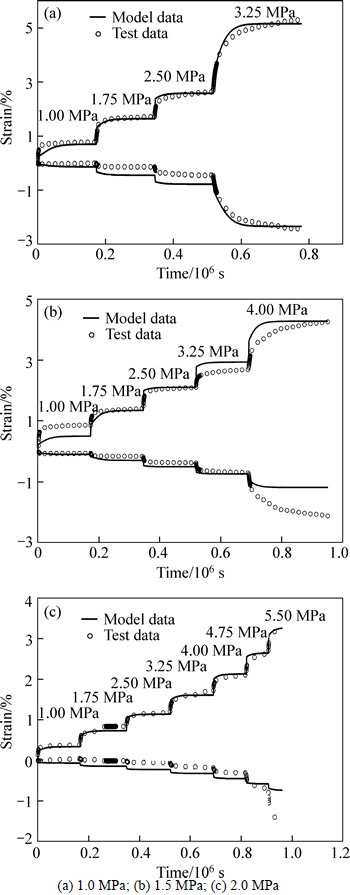
Fig. 11 Simulation of multi-loading creep tests under different confining pressures:

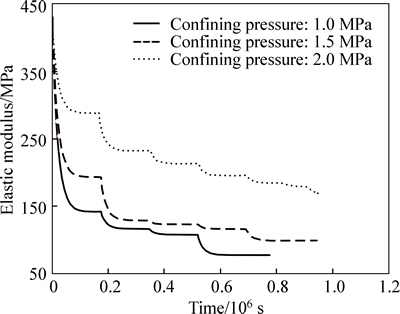
Fig. 12 Diminution of elastic modulus with time under different confining pressures

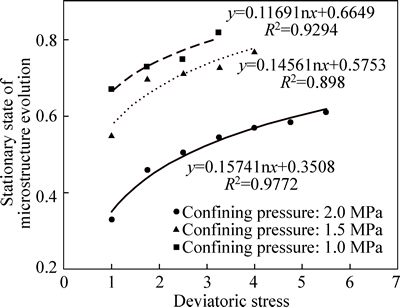
Fig. 13 Variation of 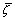under different confining pressures

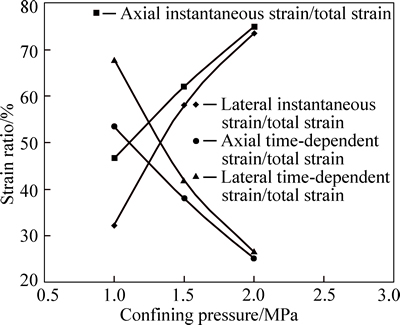
Fig. 14 Instantaneous and time-dependent strain during simulation of multi-loading creep tests

The axial instantaneous strain is larger than lateral instantaneous strain, which indicated that the effect of load on lateral instantaneous strain is lower than that on axial instantaneous strain. However, the axial time- dependent strain is smaller than lateral time-dependent strain. It is shown that the effect of creep on lateral time-dependent strain is bigger than that on axial time-dependent strain. The difference between axial strain and lateral strain decreases gradually with an increase in confining pressure. Therefore, the lateral strain can be a good indicator of microstructure evolution of rock.

5 Conclusions

A unified constitutive model is proposed to describe the instantaneous and time-dependent behaviors of weak sandstones. Starting from an elastoplastic model for the instantaneous behavior description, a creep model for the time-dependent behavior is logically formulated from elastoplastic model extension. The time-dependent behavior is described numerically by the progressive degradations of the elastoplastic properties and failure coefficient of microstructure with time. Comparisons between the numerical simulations and laboratory test have been presented for various triaxial compression and multi-loading creep tests. The proposed model is able to describe the main features of the mechanical behavior of the weak sandstone, such as plastic deformation, pressure sensitivity, plastic compressibility–dilation transition, degradation of elastic properties and failure coefficient. The proposed model can be adopted to describe other time-dependent behaviors, such as the relaxation test, unloading creep test, and constant-strain rate test, although only the triaxial compression and creep tests are simulated in the present study.

Acknowledgments

Thanks are given to Prof. J. F. SHAO for his valuable suggestions and English improvement of this manuscript, who comes from LML (Laboratoire de Mécanique des Lille) of Lille 1.

References

[1] MA L, DAEMEN J J K. An experimental study on creep of welded tuff [J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(1): 282-291.

[2] TSAI L S, HSIEH Y M, WENG M C, HUANG T H, JENG F S. Time-dependent deformation behaviors of weak sandstones [J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45: 144-154.

[3] MARANINI E, BRIGNOLI M. Creep behaviour of a weak rock: Experimental characterization [J]. International Journal of Rock Mechanics & Mining Sciences, 1999, 36(1): 127-138.

[4] ZHANG Y, XU W Y, GU J J, WANG W. Triaxial creep tests of weak sandstone from the deflection zone of high dam foundation [J]. Journal of Central South University, 2013, 20(8): 2528-2536.

[5] ZHANG Z L, XU W Y, WANG W. Triaxial creep tests of rock from the compressive zone of dam foundation in Xiang-jiaba Hydropower Station [J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 50(1): 133-139.

[6] BRANTUT N, HEAP M J, MEREDITH P G, BAUD P. Time-dependent cracking and brittle creep in crustal rocks: A review [J]. Journal of Structural Geology, 2013, 52: 17-43.

[7] BOUKHAROV G N, CHANDA M W, BOUKHAROV N G.. The three processes of brittle crystalline rock creep [J]. International Journal of Rock Mechanics & Mining Sciences, 1995, 32(4): 325-335.

[8] MAZLOOM M, RAMEZANIAN P A A. Time-dependent behavior of concrete columns containing silica fume [J]. IJCE, 2004, 2(1): 23-31.

[9] CHEN Y L, AZZAM R. Creep fracture of sandstones [J]. Theoretical and Applied Fracture Mechanics, 2007, 47: 57-67.

[10] MAIN I G. A damage mechanics model for power law creep and earthquake aftershocks and foreshock sequences [J]. Geophys J Int, 2000, 142(1): 151-161.

[11] AMITRANO D, HELMSTETTER A. Brittle creep, damage, and time to failure in rocks [J]. J Geophys Res, 2006, 111, B11201, doi:10.1029/2005JB004252.

[12] HEAP M J, BAUD P, MEREDITH P G, BELL A F, MAIN I G. Time-dependent brittle creep in Darley Dale sandstone [J]. J Geophys Res, 2009, 114, B07203, doi:10.1029/2008JB006212.

[13] DUSSEAULT M B, FORDHAM C J. Time dependent behaviour of rocks, Comprehensive Rock Engineering: Principles, practice and projects [J]. Oxford: Pergamon Press, 1993: 119-149.

[14] ZHANG H B, WANG Z Y, ZHENG Y L, DUAN P J, DING S L. Study on tri-axial creep experiment and constitutive relation of different rock salt [J]. Safety Science, 2012, 50: 801-805.

[15] YIN J H, TONG F. Constitutive modelling of the time-dependent stress-strain behaviour of saturated soils exhibiting both creep and swelling [J]. Canadian Geotechnical Journal, 2011, 48(12): 1870- 1885.

[16] YANG W D, ZHANG Q Y, LI S C, WANG S G.. Time-dependent behavior of diabase and a nonlinear creep model [J]. Rock Mechanics and Rock Engineering, 2014, 47(4): 1211-1224.

[17] ZHAO Y L, CAO P, WANG W J, WAN W, LIU Y K. Viscoelasto-plastic rheological experiment under circular increment step load and unload and nonlinear creep model of soft rocks [J]. Journal of Central South University of Technology, 2009, 16(1): 488-494.

[18] BODAS F T M, POTTS D M, ZDRAVKOVIC L. A time dependent constitutive model for soils with isotach viscosity [J]. Computers and Geotechnics, 2011, 38(6): 809-820.

[19] ZIARI H, DIVANDARI H. Presenting asphalt mixtures flow number prediction model using gyratory curves [J]. IJCE, 2013, 11(2): 125-133.

[20] XIE S Y, SHAO J F. An experimental study and constitutive modeling of saturated porous rocks [J]. Rock Mechanics and Rock Engineering, 2015, 48(1): 223-234.

[21] BONINI M, DEBERNARDI D, BARLA M, BARLA G. The mechanical behaviour of clay shales and implications on the design of tunnels [J]. Rock Mechanics and Rock Engineering, 2009, 42(2): 361-388.

[22] BRANTUT N, BAUD P, HEAP M J, MEREDITH P G. Micromechanics of brittle creep in rock [J]. J Geophys Res, 2012, 117, B08412, doi:10.1029/2012JB009299.

[23] BARLA G, DEBERNARDI D, STERPI D. Time-dependent modeling of tunnels in squeezing conditions [J]. International Journal of Geomechanics, 2012, 12(6): 697-710.

[24] BOURGEOIS F, SHAO J F, OZANAM O. An elastoplastic model for unsaturated rocks and concrete [J]. Mechanics Research Communications, 2002, 29: 383-390.

[25] HAUPT P, KERSTEN T. On the modelling of anisotropic material behaviour in viscoplasticity [J]. International Journal of Plasticity, 2003, 19: 1885-1915.

[26] VOYIADJIS G, ALRUB R, PALAZOTTO A. Thermodynamic framework for coupling of non-local viscoplasticity and non-local anisotropic viscodamage for dynamic localization problems using gradient theory [J]. International Journal of Plasticity, 2004, 20: 981-1038.

[27] ZHOU H W, WANG C P, HAN B B, DUAN Z Q. A creep constitutive model for salt rock based on fractional derivatives [J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 48: 116-121.

[28] SALEEB A F, ARNOLD S M. Specific hardening function definition and characterization of a multi mechanism generalized potential- based viscoelastoplasticity model [J]. International Journal of Plasticity, 2004, 20: 2111-2142.

[29] PIETRUSZCZAK S, LYDZBA D, SHAO J F. Modelling of inherent anisotropy in sedimentary rocks [J]. International Journal of Solids and Structures, 2002, 39: 637-648.

[30] PIETRUSZCZAK S, LYDZBA D, SHAO J F. Description of creep in frictional materials in terms of microstructure evolution [J]. Journal of Engineering Mechanics, 2004, 130(6): 681-690.

[31] SHAO J F, ZHU Q Z, SU K. Modeling of creep in rock materials in terms of material degradation [J]. Computers and Geotechnics, 2003, 30: 549-555.

[32] SHAO J F, JIA Y, KONDO D, CHIARELLI A S. A coupled elastoplastic damage model for semi-brittle materials and extension to unsaturated conditions [J]. Mechanics of Materials, 2006, 38: 218-232.

[33] ZHANG Y, SHAO J F, XU W Y, ZHAO H B, WANG W. Experimental and numerical investigations on strength and deformation behavior of cataclastic sandstone [J]. Rock Mechanics and Rock Engineering, 2015, 48(3): 1083-1096.

[34] ZHANG Y, SHAO J F, XU W Y, JIA Y. Time-dependent behavior of cataclastic rocks in a multi-loading triaxial creep test [J]. Rock Mechanics and Rock Engineering, 2016, 49(9): 3793-3803.

(Edited by YANG Hua)

Cite this article as: WANG Jing-yin, ZHANG Yu, JIA Yun, JIN Pei-jie, ZHU Li-hong. Elastoplastic modeling of mechanical behavior of weak sandstone at different time scales [J]. Journal of Central South University, 2017, 24(3): 699-707. DOI: 10.1007/s11771-017-3471-3.

Foundation item: Project(51409261) supported by the National Natural Science Foundation of China; Projects(ZR2014EEQ014) supported by the Natural Science Foundation of Shandong Province, China; Projects(16CX05002A, 15CX05039A) supported by the Fundamental Research Funds for the Central Universities of China

Received date: 2015-07-24; Accepted date: 2015-11-06

Corresponding author: ZHANG Yu, Associate Professor; Tel: +86-13792839259; E-mail: zhangyu@upc.edu.cn