基于JRC-JCS模型的边坡局部稳定性分析
万世明,吴启红,谢飞鸿,杨有莲
(成都大学 城乡建设学院,四川 成都,610106)
摘要:为了建立JRC-JCS模型下的点安全系数计算方法,并对岩体边坡各部位稳定性进行评判,首先推导基于JRC-JCS模型的非线性点安全系数计算公式。然后,研究JRC-JCS模型参数对于点安全系数的影响,并通过算例分析,编制相应的点安全系数程序,应用于边坡各部位岩土体的稳定性分析中。研究结果表明:编制的计算程序的结果与FLAC3D的计算结果一致,从而验证了程序的正确性,并且该程序结果能够反映边坡岩体各部位的稳定情况。
关键词:JRC-JCS模型;边坡;稳定性;点安全系数
中图分类号:TU821 文献标志码:A 文章编号:1672-7207(2014)04-1227-05
Local stability analysis for slope based on JRC-JCS model
Wan shiming, WU Qihong, XIE Feihong, YANG Youlian
(School of Urban and Rural Construction, Chengdu University, Chengdu 610106, China)
Abstract: In order to build the calculation method of point safety factor based on JRC-JCS model, and to estimate the stability of each part of rock slope, firstly, the calculation formulation of nonlinear point safety factor based on JRC-JCS model was founded, and then the effect of parameters of JRC-JCS model to the point safety factor was studied. And through calculation example, the program of point safety factor was compiled in the application of stability analysis for each part of rock slope. The calculation results show that the results from the compiled program is in accordance with the FLAC3D calculation results, which has verified the correctness of the program, and the program results can reflect the stability of each part of rock slope.
Key words: JRC-JCS model; slope; stability; point safety factor
边坡稳定性是岩土工程的重要研究内容之一,目前一般采用整体安全系数对边坡稳定性进行评判[1-3],这种方法无法反映边坡各部位的安全状况,因此,在边坡支护过程中就需要进行整体加固,从而造成浪费。实际上,许多边坡的失稳往往是局部失稳引发整体失稳的,此时,若能够加固这些危险部位,则可防止边坡的整体失稳,因此,研究边坡岩土体各部位的稳定情况成为必要。一些学者也意识到这个问题,并引入点安全系数或者屈服接近度的概念来评判岩土体各部位的安全状况,如Hoek等[4]最先将点安全系数引入到边坡稳定分析中。把点安全系数定义为岩土体中一点所能调动的最大剪切强度与该点可能出现的剪应力之比;沈可等[5]推导了基于Mohr-Coulomb模型(MC模型)的空间点安全系数公式;蓝航[6]引入静载强度分析研究了点安全系数计算方法;李树忱等[7]根据弹性理论,利用MC和Drucker- Prager模型(DP模型),采用点安全系数建立了隧道围岩稳定评价指标。张传庆等[8-9]定义了Mohr-Coulomb准则下的屈服接近度指标,并建立了屈服接近度求解函数,对围岩中非塑性区的危险程度进行了定量研究。这些研究主要基于MC或者DP等线性模型,对岩体稳定评价做出了有意义的贡献,但岩体不同于金属材料,其中广泛分布着结构面,导致其强度呈现非线性特征[10],而线性模型无法反映该特征,存在一定局限性。因此,需开发基于非线性模型的边坡安全系数计算方法,一些学者基于Hoek-Brown模型做了有意义的工作,如林杭等[11-12]扩展了强度折减法在Hoek-Brown准则中的应用;蒋青青[13]建立了Hoek-Brown非线性模型下的边坡稳定性点安全系数。而对于节理岩体,普遍认为JRC-JCS模型(JJ模型)能够较好描述节理岩体特征[14-16],若能建立该模型下的点安全系数计算方法对岩体边坡各部位稳定性进行评判,具有一定工程和理论意义。基于以上考虑,本文作者首先推导了MC模型下点安全系数的计算方法,然后,建立JJ模型参数和MC模型参数的关系,从而得到基于JJ模型的非线性点安全系数计算公式。最后,研究JJ模型参数对于点安全系数的影响,并通过算例分析,编制相应的点安全系数程序,应用于边坡各部位岩土体的稳定性分析中。
1 JRC-JCS模型点安全系数
边坡岩土体单元应力的屈服(破坏)条件为:
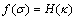 (1)
(1)
式中:f为应力函数关系;σ为应力组合;H为材料参数函数关系;κ为材料参数的内变量。
为了表征岩体单元的安全情况,引入安全系数的概念,其表达式为[13]:
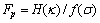 (2)
(2)
通过计算得到相应单元应力值,以及材料参数值,并代入式(2),即可得到点安全系数Fp。Fp能够描述岩体单元的破坏程度,其受岩体参数、岩体内应力分布以及强度模型的影响。Fp>1表征岩体单元的应力状态未导致单元发生破坏,岩体处于稳定状态;Fp<1表征的情况与Fp>1的情况相反;Fp=1表征岩体处于临界稳定状态。
为了在JJ模型中建立相应的点安全系数计算公式。取出单元的一个计算剖面,可得到该面上的剪应力和剪切强度,当剪应力大于抗剪强度时,单元将沿该面发生剪切破坏。图1所示为岩体单元的Mohr应力圆,任一面上的应力情况为
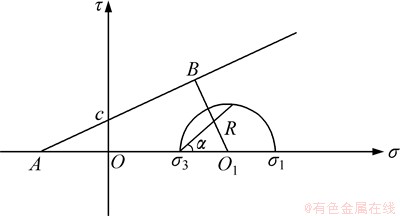
图1 应力Mohr圆
Fig. 1 Stress Mohr circle
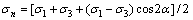 (3)
(3)
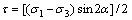 (4)
(4)
式中:σn为该面上的法向应力;τ为面上的剪切应力;σ1,σ3为单元的最大和最小主应力;α为该面与最小主平面的夹角。
该面上的剪切强度τc为
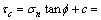
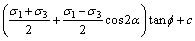 (5)
(5)
式中:f和c分别为岩体的内摩擦角和黏结力。
联立式(2)~(5),可得点安全系数的表达式:
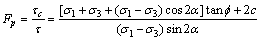 (6)
(6)
从式(6)可知:点安全系数是关于α角的函数,因此,为了得到Fp的最小值以确定岩体单元点的稳定情况,对α进行求导。
令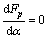 ,可得:
,可得:
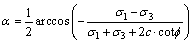 (7)
(7)
将式(7)代入式(6),即可确立Fp的计算公式:
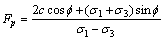 (8)
(8)
从式(8)可以看出:MC模型中,点安全系数主要取决于岩体的强度参数黏结力和内摩擦角。因此,为了在JJ模型中推广点安全系数,只需确立JJ模型参数与MC准则参数之间的关系,然后,将所确立的参数代入式(8)即可得到基于JJ模型参数的点安全系数计算公式。
具体推导如下:
JJ模型是巴顿通过大量节理岩体的剪切试验提出的[15],其形式为
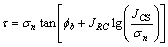 (9)
(9)
式中:τ为岩体的剪切强度;σn为节理的正应力;fb为岩体基本摩擦角,可取为30°的定值[16];JRC为节理粗糙系数;JCS为岩体压缩强度,低应力条件下JCS对抗剪强度影响较小,随法向应力增大,JCS的影响亦增大。
由于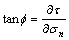 [13],
[13],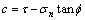 ,求导式(9),可得
,求导式(9),可得
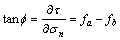 (10)
(10)
式中: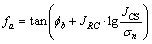 ;
;
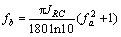 。
。
对式(10)进行三角关系变换,
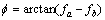 (11)
(11)
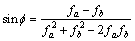 (12)
(12)
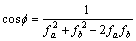 (13)
(13)
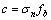 (14)
(14)
式中: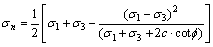 。
。
从fa的计算公式中可以看出:当σn→0时,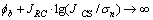 ,显然这是不成立的。因此,Barton等[15]建议:在实际工程应用中,
,显然这是不成立的。因此,Barton等[15]建议:在实际工程应用中,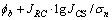 不应该大于70°。法向应力的极小值可用
不应该大于70°。法向应力的极小值可用 =70°反算得到,即,
=70°反算得到,即,
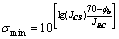 (15)
(15)
对于边坡岩土体,可参考Hoek等[4]的建议得到法向应力的最大值,
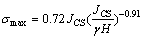 (16)
(16)
式中:γ为岩体容重;H为边坡高度。
将式(9)~(11)代入式(6)即可得到JJ模型的点安全系数Fp计算公式:
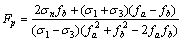 (17)
(17)
2 算例分析
2.1 JRC和JCS对Fp的影响
取出边坡岩体中某单元的应力σ1=1.0 MPa,σ3=0.4 MPa,边坡高为20 m,容重γ=26.0 kN/m3,分别改变材料参数JCS和JRC,分析各个参数对Fp的影响。假设岩体的基本摩擦角为30°,固定JCS=20 MPa,令JRC=0~20,得到图2;固定JRC=6,令JCS=5~105 MPa,得到图3。从图2和图3可以看出:随着JRC和JCS的增大,岩体点安全系数Fp均呈现非线性增大,可通过指数方程对其关系进行拟合,得到的相关系数分别为0.993 57和0.997 72,属于高度相关;Fp与JRC关系曲线的斜率随JRC的增大而增大,而Fp与JCS关系曲线的斜率随JCS的增大而减小。
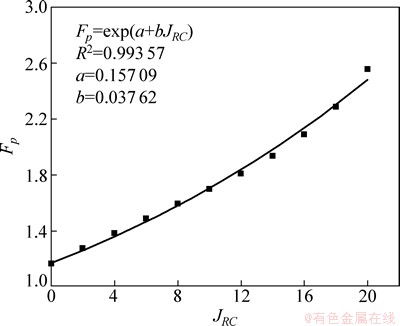
图2 JRC对Fp的影响
Fig. 2 Effect of JRC to Fp
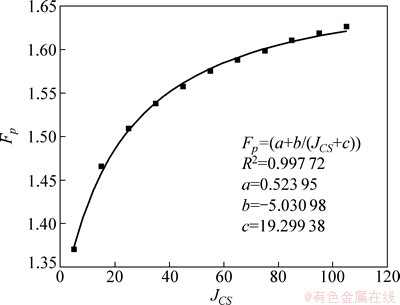
图3 JCS对Fp的影响
Fig. 3 Effect of JCS to Fp
2.2 算例分析
某边坡高20 m,建立节理概化模型,整体模型长60 m,宽10 m,高40 m,单元数15 000,节点数17 391;边界条件为:底部固定约束,四周约束法向位移,上部为自由边界。初始应力场按自重应力考虑;计算收敛准则为不平衡力比率(节点平均内力与最大不平衡力的比值)满足10-6的求解要求。计算参数为:弹性模量E=0.5 GPa,泊松比μ=0.28,容重γ=26.0 kN/m3。剪切模量G和体积模量K通过式(18)和(19)计算可得:
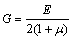 (18)
(18)
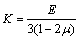 (19)
(19)
强度参数设置2个方案:(1) fb=30°,JCS=20 MPa,JRC=2;(2) fb=30°,JCS=50 MPa,JRC=12。
数值计算过程中,根据弹性理论计算各个单元的应变及应力,然后,代入强度模型进行判断,若达到了屈服条件,则进行相应的应力调整,使应力满足屈服函数,即使得单元体的应力状态回到应力空间中的屈服面上,具体可参考文献[17]。
通过差分法计算,根据式(17)利用FISH语言编制相应的点安全系数程序,得到的结果如图4所示。从图4可以看出:在靠近边坡开挖面位置,由于边坡开挖使围岩约束消失,岩体存在向边坡内运动的趋势,因此该部位的单元安全程度最低,部分区域的安全系数甚至小于1,由于FLAC3D计算得到的塑性区表征的是安全系数小于1的单元,因此将其与点安全系数公式计算得到的Fp≤1的区域进行对比,可以验证点安全系数公式的正确性,通过对比发现二者的分布范围相同。另外,方案1岩体的强度小于方案2岩体的强度,引起边坡各部位的安全系数小于方案2的情况。
从本文的推导以及数值计算过程中可以看出:本文推导的关于JRC-JCS模型下的点安全系数的计算公式,以及相应的数值计算程序主要是针对均质边坡而言的,若边坡中含有节理面或其他不连续面时,需考虑岩土体材料的非均匀性。
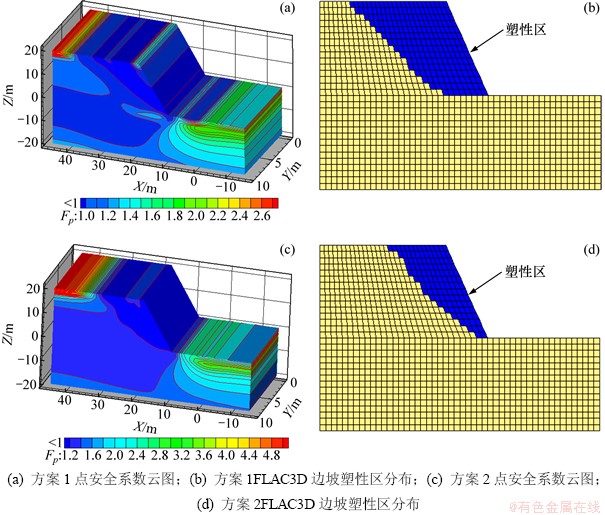
图4 计算结果
Fig. 4 Calculation results
3 结论
(1) 推导得到了基于JRC-JCS模型的非线性点安全系数计算公式。
(2) 在理论推导的基础上,利用FISH语言编制了计算程序,对比点安全系数Fp≤1的区域与FLAC3D自身计算的塑性区分布范围,二者基本一致,从而验证了自编程序的正确性,并且该程序结果能够反映边坡岩体各部位的稳定情况。
参考文献:
[1] Griffiths D V, Lane P A. Slope stability analysis by finite elements[J]. Geotechnique, 1999, 49(3): 387-403.
[2] 赵尚毅, 郑颖人, 邓卫东. 用有限元强度折减法进行节理岩质边坡稳定性分析[J]. 岩石力学与工程学报, 2003, 22(2): 254-260.
ZHAO Shangyi, ZHENG Yingren, DENG Weidong. Stability analysis on jointed rock slope by strength reduction[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 254-260.
[3] Dawson E M, Roth W H, Drescher A. Slope stability analysis by strength reduction[J]. Geotechnique, 1999, 49(6): 835-840.
[4] Hoek E, Bray J. Rock slope engineering[M]. London: Institute of Mineral and Metallurgy, 1981: 60-92.
[5] 沈可, 张仲卿. 三维抗滑稳定分析中的点安全系数法[J]. 人民珠江, 2003(2): 21-22.
SHEN Ke, ZHANG Zhongqing. Point safety factor method for 3-dimensional stability analysis[J]. Pearl River, 2003(2): 21-22.
[6] 蓝航. 基于FLAC3D的边坡单元安全度分析及应用[J]. 中国矿业大学学报, 2008, 37(4): 570-574.
LAN Hang. Analysis of zone safety degree of slopes and its application based on FLAC3D[J]. Journal of China University of Mining & Technology, 2008, 37(4): 570-574.
[7] 李树忱, 李术才, 徐帮树. 隧道围岩稳定分析的最小安全系数法[J]. 岩土力学, 2007, 28(3): 549-554.
LI Shuchen, LI Shucai, XU Bangshu. Minimum safety factor method for stability analysis of surrounding rock mass of tunnel[J]. Rock and Soil Mechanics, 2007, 28(3): 549-554.
[8] 张传庆, 周辉, 冯夏庭. 基于破坏接近度的岩土工程稳定性评价[J]. 岩土力学, 2007, 28(5): 888-894.
ZHANG Chuanqing, ZHOU Hui, FENG Xiating. Stability assessment of rockmass engineering based on failure approach index[J]. Rock and Soil Mechanics, 2007, 28(5): 888-894.
[9] 张传庆, 周辉, 冯夏庭, 等. 基于屈服接近度的围岩安全性随机分析[J]. 岩石力学与工程学报, 2007, 26(2): 292-299.
ZHANG Chuanqing, ZHOU Hui, FENG Xiating, et al. Stochastic analysis method on safety of surrounding rock mass based on yielding approach index[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(2): 292-299.
[10] Barton N, Pandey S K. Numerical modelling of two stoping methods in two Indian mines using degradation of c and mobilization of φ based on Q-parameters[J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 48(7): 1095-1112.
[11] 林杭, 曹平, 赵延林, 等. 强度折减法在Hoek-Brown准则中的应用[J]. 中南大学学报(自然科学版), 2007, 38(6): 1219-1224.
LIN Hang, CAO Ping, ZHAO Yanlin, et al. The application of strength reduction method in Hoek-Brown criterion[J]. Journal of Central South University (Science and Technology), 2007, 38(6): 1219-1224.
[12] 林杭, 曹平, 李江腾, 等. 基于广义Hoek-Brown准则的边坡安全系数间接解法[J]. 煤炭学报, 2008, 33(10): 1147-1151.
LIN Hang, CAO Ping, LI Jiangteng, et al. The indirect calculation method for the safety factor of slope based on generalized Hoek-Brown criterion[J]. Journal of China Coal Society, 2008, 33(10): 1147-1151.
[13] 蒋青青. 基于Hoek-Brown 准则点安全系数的边坡稳定性分析[J]. 中南大学学报(自然科学版), 2009, 40(3): 786-790.
JIANG Qingqing. Stability of point safety factor of slope based on Hoek-Brown criterion[J]. Journal of Central South University (Science and Technology), 2009, 40(3): 786-790.
[14] 赵坚. 岩石节理剪切强度的JRC-JMC新模型[J]. 岩石力学与工程学报, 1998, 17(4): 349-357.
ZHAO Jian. A new JRC-JMC shear strength criterion for rock joint[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(4): 349-357.
[15] Barton N, Choubey V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics, 1977(10): 1-54.
[16] 杜时贵, 郭霄, 颜育仁. JRC-JCS模型在抗剪强度参数取值中的应用[J]. 金华职业技术学院学报, 2004, 4(1): 1-4.
DU Shigui, GUO Xiao, YAN Yuren. JRC-JCS model and its application on studying shear strength of rock joint[J]. Journal of Jinhua College of Profession and Technology, 2004, 4(1): 1-4.
[17] Itasca Consulting Group. User’s Guid[M]. Minnesota: Itasce Consulting Group, 2002: 152-156.
(编辑 杨幼平)
收稿日期:2013-05-11;修回日期:2013-07-23
基金项目:国家自然科学基金资助项目(50878212);四川省科技计划项目(2013JY0119)
通信作者:吴启红(1981-),男,四川乐至人,博士,副教授,从事岩土工程及地质工程研究;电话:18628066800;E-mail:wqh1016@126.com