基于孔隙介质中弹性波速理论的结构损伤识别与成像
郭少华,郭原草
(中南大学 土木工程学院,湖南 长沙,410004)
摘要:基于规范空间理论研究各向异性固体运动方程与含水介质质量守恒方程的准静态耦合问题,讨论几种不同各向异性性质的孔隙介质的弹性波传播规律,分析波场速度在结构损伤区域的变化规律,最后采用偏移技术对结构损伤进行成像,提出一个新的可压缩空隙弹性介质的本构方程,在此基础上得到一组完全解耦的各向异性含水孔隙介质的弹性波方程。研究结果表明:各向异性含水孔隙介质的弹性波速即取决于固体骨架的本征特性也受到流-固耦合系数的影响。
关键词:孔隙介质;各向异性;可压缩弹性模型;弹性波;偏移成像
中图分类号:TG111.3 文献标志码:A 文章编号:1672-7207(2013)10-4208-06
Structural damage identification and image based on theory of elastic wave velocity for porous medium
GUO Shaohua, GUO Yuancao
(School of Civil Engineering, Central South University, Changsha 410004, China)
Abstract: The static coupled issue of the anisotropic solid motion equation and the water saturated interstitial media conservation of mass equation were studied on the base of the normative space theory, and the elastic wave propagation theory of several different kinds of anisotropic spacing medium was discussed. The variation theory of the wave velocity in the damage region was analyzed, and the structural damage was imaged by the migration technology. A new compressed interstitial elastic media constitutive equation was presented. A group of anisotropic water saturated interstitial medium elastic wave equations were obtained. The results show that the anisotropic water saturated interstitial medium elastic wave velocity relies on the constitutive character of the solid skeleton, and it is also affected by the fluid-solid coefficient.
Key words: interstitial medium; anisotropic medium; compressed elastic model; elastic wave; migration image
一般情况下的水饱和介质弹性波理论最早由 Biot等[1-2]提出。在Biot理论中,固相和流相分别被看作是2个不同性质的连续介质,采用混合物作用模型分别推导出了固体和流体中的弹性体波传播规律,发现和解释了一些新的含水孔隙介质的波动现象[3-4]。但大多数工程地质材料(比如岩石和土介质)的固体相和流体相较难区分,也不能通过一般实验手段分别得到固体弹性波和流体弹性波的传播规律。为便于研究通常将含水孔隙介质视为具有渗流性质的孔隙弹性材料[5-7],通过连续介质力学的方法得到单一介质的弹性波传播规律,孔隙水仅仅作为影响弹性波速的因素而考虑。基于以上弹性波理论,Loewenthal等[8-9]研究了含水介质中弹性波速的变化规律,Hudson等[10-12]研究了含气体空洞中弹性波速的变化规律,Fei等[13]研究了带有裂缝或者孔隙介质中的科氏积分叠前偏移方法。Lin等[14-15]首先将地球物理勘探领域中的偏移成像方法引入到结构损伤探测中。张文生[16]进一步研究了偏移成像的数值计算方法。本文作者推导了各向异性孔隙介质的弹性波本构方程,分析了含水或者气体的孔隙介质中弹性波速变化规律并将该理论推广到带损伤板式结构内部的波速研究中。基于连续介质力学原理应用规范空间理论研究含水孔隙介质的弹性波传播过程所遵循的运动方程和质量守恒方程。其中几何表象下的张量牛顿运动方程和达西渗流方程被转换成为物理表象下的标量形式,通过引入新的可压缩弹性模型推导出非耦合形式的弹性波方程组。每一个子方程代表一个弹性子波的存在,其传播速度、传播方向和空间形态可以完全由这些模态方程确定。采用类似的偏移成像技术对板式结构中的裂缝或者孔洞损伤进行成像,初步实现了结构损伤成像可视化,对传统的结构损伤识别技术是一个有益的补充。
1 各向异性空隙介质本构方程
根据有效应力理论以及线弹性水饱和孔隙材料的可压缩关系,各项异性的孔隙介质本构关系可以写成:
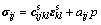 (1)
(1)
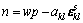 (2)
(2)
式中:p为孔隙压力;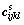 为固相弹性张量;w为压缩系数;aij为耦合系数;n为孔隙率;σij为应力张量;
为固相弹性张量;w为压缩系数;aij为耦合系数;n为孔隙率;σij为应力张量;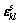 为应变张量。将方程(1)和(2)写成如下形式:
为应变张量。将方程(1)和(2)写成如下形式:
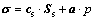 (3)
(3)
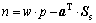 (4)
(4)
其中:固体骨架弹性矩阵cs可以谱分解为
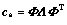 (5)
(5)
式中:Λ=diag[λ1,λ2,λ3,λ4,λ5,λ6]是固体骨架的本征弹性矩阵;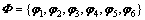 是相应的模态矩阵,它是正交正定矩阵并且满足ΦTΦ=I。将几何表象下的应力矢量σ和应变矢量S,投影到物理表象下的规范空间有:
是相应的模态矩阵,它是正交正定矩阵并且满足ΦTΦ=I。将几何表象下的应力矢量σ和应变矢量S,投影到物理表象下的规范空间有:
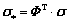 (6)
(6)
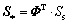 (7)
(7)
式中:σ*和σs分别为几何表征与物理表征下的应力矢量;S*和Ss分别为几何表征与物理表征下的应变矢量。将方程(6)和(7)分别代入方程(3)和(4),左乘模态矩阵的转置得:
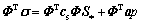 (8)
(8)
 (9)
(9)
用标量形式改写方程(8)和(9)得
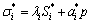 ,i=1,2,…,m (10)
,i=1,2,…,m (10)
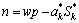 ,k=1,2,…,m (11)
,k=1,2,…,m (11)
方程(10)和(11)是各项异性含水弹性孔隙材料的模态本构方程,其中:a*k为流-固耦合系数;λi为固体本征弹性矩阵的特征值。不可压缩的稳定流体质量守恒方程为
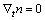 (12)
(12)
固体运动方程的模态形式为
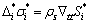 ;i=1,2,…,m (13)
;i=1,2,…,m (13)
式中: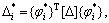 是应力算子;
是应力算子;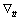 是时间二阶算子,且
是时间二阶算子,且
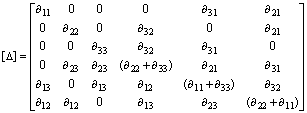 (14)
(14)
式中: 。
。
将方程(10)和(11)代入方程(12)和(13)得:
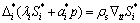 (15)
(15)
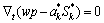 (16)
(16)
式中:ρs为液体密度。根据微分算子作用原理从方程(16)得
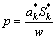 (17)
(17)
将其代入方程(15),有
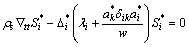 (18)
(18)
式中:△ik为Kronecker符号,将它写成标准波动方程形式:
 ,i=1,2,…,m (19)
,i=1,2,…,m (19)
其中:
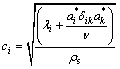 (20)
(20)
式(20)是孔隙介质的弹性波速公式。对横观各向同性介质,方程(1)和(2)中的材料张量可以写成下面的紧凑形式:
 (21)
(21)
其中: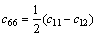 。各向同性介质的本征弹性为
。各向同性介质的本征弹性为
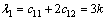 ,
,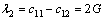 (22)
(22)
式中:K为体积弹性模量;G为剪切弹性模量。各向同性介质的耦合系数及应力算子分别为:
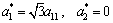 (23)
(23)
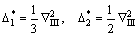 (24)
(24)
式中: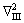 是三维Laplace 算子。
是三维Laplace 算子。
各向同性介质存在2个独立的弹性波,其传播规律分别由下面2个模态方程描述:
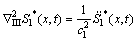 (25)
(25)
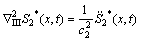 (26)
(26)
其中:
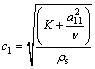 ,
,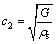 (27)
(27)
方程(25)和(26)分别表示体积波和剪切波。横观各向同性介质的本征弹性为
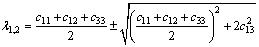 ;
;
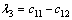 ;
;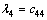 (28)
(28)
其中:
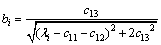 ;
;
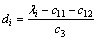 (29)
(29)
横观各向同性介质的各阶模态应变分别为:
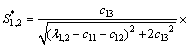
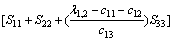 ;
;
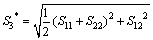 ;
;
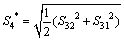 (30)
(30)
一阶和二阶模态应变分别表示弹性固体的准体积变形;三阶和四阶模态应变分别表示弹性固体的准剪切变形。各弹性子波的传播速度为:
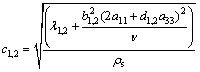 ;
;
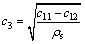 ;
;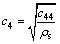 (31)
(31)
2 数值算例
建立1个铝质板式结构模型,板尺寸(长×宽)为200 cm×200 cm,密度ρ=2 710 kg/m,泊松比μ=0.3,板厚h=0.16 cm,抗拉弹性模量E=72.5 GPa;结构内部损伤由常速介质中的裂缝(界面)或者圆形空洞组成,裂缝尺寸设定为长度L=2 cm,宽度a=2 mm。圆形空洞与夹杂半径R=2 cm,直径d=4 cm,固相快纵波波速vspf=3.668 km/s,固相慢纵波波速vsps=3.324 km/s,固相横波波速vst=2.098 km/s,液相快纵波波速vspf=2.789 km/s,液相慢纵波波速vsps=2.654 km/s,液相横波波速vft=1.898 km/s。5个不同方向固相弹性张量分量为c11=2.1 GPa,c21=1.4 GPa,c23=1.6 GPa,c13=1.8 GPa,c33=2.0 GPa;体积弹性模量K=14.2 GPa,剪切弹性模量G=20.3 GPa,这里采用偏移技术和有限差分网格法实现损伤成像。x方向与z方向采样率△x=△z=0.5 m,时间采样率△t=2 ms时间样点数为250,空间样点数为90×90。波场震源频率f=40 Hz。
图1~4所示为弹性波速度在结构损伤区域内部传播过程中的变化曲线。在不同波场入射角度、波数以及裂缝长细比或者孔洞直径下,波场速度也表现出不同变化规律。当波场沿结构纵向传播到6,12和19 cm位置时波速曲线都出现了很深的凹陷形状,波速迅速降低到极小值1.3 km/s;当波场通过这几个特殊位置后波速迅速恢复到正常值3.0 km/s。波速变化曲线的这些显著特征表明结构内部存在的损伤导致波速在损伤位置处发生显著变化,变化方向和趋势则取决于损伤与结构密度以及结构损伤的形态。若损伤形态为裂缝或者空洞,内部含水或空气,则波速显著降低;若损伤形态为高密度杂质,则波速出现显著提高。损伤如果相对于结构材料较软,则波速一般会有不同程度的降低;若结构损伤相对于结构材料较硬,则波速通常会显著增加。图1中波速曲线中在6,12和19 cm位置时存在明显的低谷,极小值v=1.3 km/s,图2中波速曲线中在1.5,3.0和4.5 cm位置时存在明显的低谷,极小值v=1.1 km/s,说明在这3个位置存在含水或空气的裂缝或者孔洞损伤;图3和图4中波速分别在纵向0.5和0.8 cm位置时出现极大值4.0和9.0 km/s,而波场通过此处后波速迅速降低到正常值。因此,可以推断在0.5和0.8 cm位置处即波速峰值处存在高密度杂质。根据波速出现异常变化的纵横向位置可以确定内部损伤的大致位置。根据波速曲线变化形状还可以大致确定损伤形态,若在波速变化曲线出现了平坦的凹陷区说明波速在一个较长的距离内都有显著降低,则此损伤通常可判断为裂缝;若速度曲线上出现点状、尖锐状或者窄条状峰值,则损伤形式多为单个孔洞或者高密度杂质。若曲线是向上突起的尖峰,状则损伤为高密度夹杂;若曲线是向下凹陷的深沟状,则为空洞损伤。
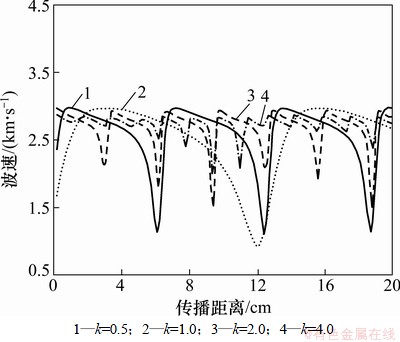
图1 h/R=1.5时波场速度随传播距离变化曲线
Fig. 1 Variation curve between wave velocity and distance when h/R=1.5
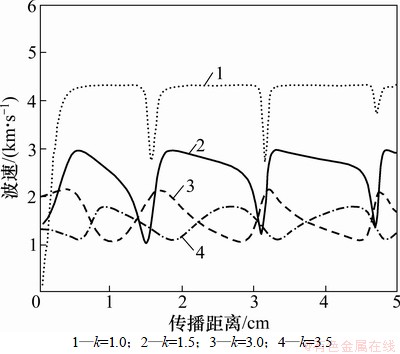
图2 h/R=2.0时波场速度随传播距离变化曲线
Fig. 2 Variation curve between wave velocity and distance when h/R=2.0
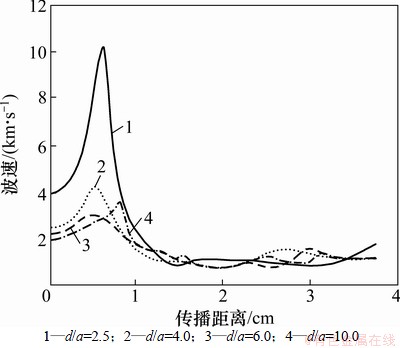
图3 α=45°时波场速度随传播距离变化曲线
Fig. 3 Variation curve between wave velocity and distance when α=45°
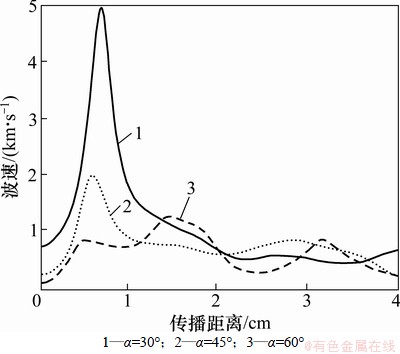
图4 d/a=4.0时波场速度随传播距离变化曲线
Fig. 4 Variation curve between wave velocity and distance when d/a=4.0
图5和图6所示为波场速度极坐标分布图。从图5和图6可见:随着波场入射角度、波数以及裂缝长细比随着空洞夹杂的直径不同,其波速沿着损伤周围大致成蝴蝶状对称分布。首先考虑波数对波速分布图的影响;当波数k=4.0时,波速沿着对称轴α=90°呈圆形分布;当波数由4.0逐渐减小到0.5时,波速分布曲线沿着横轴α=0°逐渐变得扁平,说明当波数逐渐增大时水平方向波速变化范围逐渐扩大而垂直方向波速变化范围逐渐减小;当波数k=1.0、裂缝损伤的长细比h/R=2.0、入射角度α=135°时,波速达到极大值v=1.1 km/s;当波数k=2.0、入射角度α=225°时,波速达到极小值v=-1.2 km/s。波速符号发生了改变,说明此时波场在结构损伤表面发生了较强的反射现象,当时反射波速达到负极大值时反射现象也最强,波场衍射现象也最弱。因此,通过波场绕射衍射现象来判断结构损伤的效果欠佳。当波场入射角α=30°时,波速呈关于α=120°轴对称的2个圆分布。当α=30°时,波速达到极大值v=2.0 km/s。当入射角α=60°时,波速呈关于α=150°轴对称的2个圆分布,此时波速极大值v=1.8 km/s,若入射角α=90°或0°,此时波场垂直于或平行于损伤入射,波速分布图变为1个圆,此时波场衍射效果最差,用以进行损伤识别与成像的效果也最差。
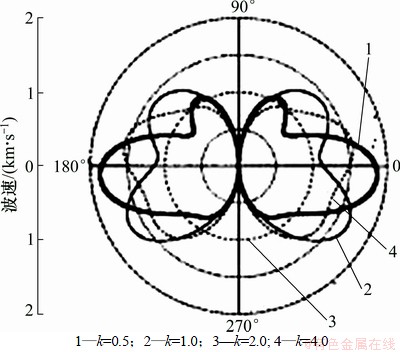
图5 h/R=1.5时波场速度分布图
Fig. 5 Distribution of wave velocity when h/R=1.5
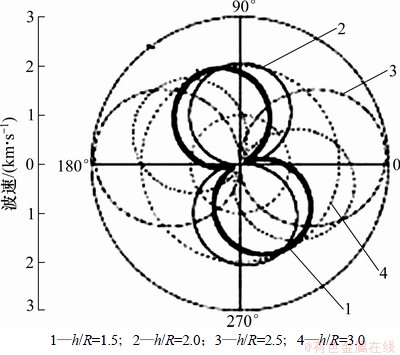
图6 α=30°时波场速度分布图
Fig. 6 Distribution of wave velocity when α=30°
图7和图8所示为采用偏移叠加技术得到的不同时刻的波场损伤区域快照图。在图7和图8中可以识别出明显的半圆弧形花纹特征,这些花纹特征均由波场衍射和绕射现象引起。当波场传播结构内部的损伤位置时,波场会在损伤界面处同时产生绕射、反射与衍射等现象,在相应的波场快照上就会形成花纹状图案。随着波场逐渐通过损伤区域,这种波场衍射和绕射现象也逐渐削弱,半圆弧形的花纹效果逐步减弱,快照中波场形态逐渐恢复到原来的正常状态,这表明波场重新进入结构无损伤区域。根据波场快照中衍射波出现的区域和对应的时刻可以判定结构内部损伤位置[17];损伤形态不同产生的衍射波场也不同,在波场快照上出现的花纹形状和范围也不同。但总体上,衍射波场以及花纹形状与结构损伤形态大致相同,这就使得结构损伤识别初步实现了可视化应用。为进一步提高损伤的偏移成像清晰度,通常需要相应地提高有限差分网格的精确度并采用合适的边界吸收条件。
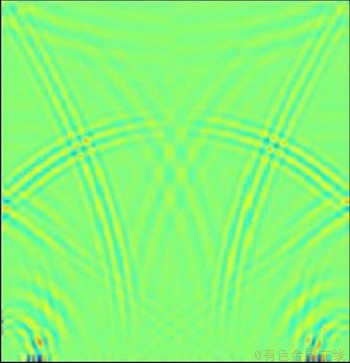
图7 t=154 μs时波场水平速度快照图
Fig. 7 Snapshot of horizontal velocity when t=154 μs
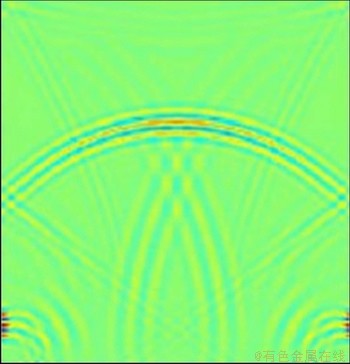
图8 t=169 μs时波场垂直速度快照图
Fig. 8 Snapshot of vertical velocity when t=169 μs
3 结论
(1) 各向异性含水孔隙介质的弹性波速取决于固体骨架的本征弹性,但流-固耦合系数仅仅影响弹性体波的传播性质,而对剪切波传播特性没有影响。
(2) 波场经过结构损伤区域时波场速度会出现显著变化,变化趋势随着损伤形态以及软硬程度而不同。当结构损伤相对于结构材料较硬时,波速明显上升,反之,则明显下降。
(3) 波速分布随着结构损伤的形态和位置呈现出不同的分布规律。波速沿着损伤周围大致成蝴蝶状对称分布。当波数逐渐增大时,横波速度变化范围逐渐扩大而纵波速度变化范围逐渐减小。
(4) 结构内部损伤会引起波场衍射和绕射等异常现象,衍射现象在快照中表现为各种形态的花纹与阴影,根据花纹与阴影的位置与形态可以判断出结构内部损伤的位置和形态。
参考文献:
[1] Biot M. Theory of propagation of elastic waves in a fluid-saturated porous solid: I. Low-frequency range[J]. Acoustical Society of America, 1956, 28(2): 168-178.
[2] 艾龙根, 舒胡毕. 弹性动力学: 线性理论[M]. 戈革, 译. 北京: 石油工业出版社, 1983: 96-117.
Eringen A C, Shuhubi E S. Elastodynamics: Linear theory[M]. GE Ge, trans. Beijing: Petroleum Industrial Press, 1983: 96-117.
[3] 黄克智. 板壳理论[M]. 北京: 清华大学出版社, 1987: 89-112.
HUANG Kezhi. The theory of the plate and shell[M]. Beijing: Tsinghua University Press, 1987: 89-112.
[4] Wapenaar C P A, Kinneging N A, Berkhout A J. Principle of prestack migration based on the full elastic two way wave equation[J]. Geophysics, 1987, 52(2): 151-173.
[5] Ruhl T. Finite difference migration derived from the Kirchhoff Helmholtz integral[J]. Geophysics, 1996, 61(5): 1394-1399.
[6] Bleistein N. On the imaging of reflectors in the earth[J]. Geophysics, 1987, 52(7): 931-942
[7] DAI Nanxun, Vadidis A, Kanasewich E R. Seismic migration and absorbing boundaries with a one way wave system for heterogenous media[J]. Geophysical Prospecting, 1996, 44(2): 719-739.
[8] Loewenthal D, Lu L, Roberson R, Sherwood J. The wave equation applied to migration[J]. Geophysical Prospecting, 1976, 24(2): 380-390.
[9] Loewenthal D, Mufti I R. The reversed time migration in spatial frequency domain[J]. Geophysics, 1983, 48(5): 627-635.
[10] Hudson J A. A higher order approximation to the wave propagation constants for a cracked solid[J]. Geophysical Journal Internation, 1986, 87(1): 265-274.
[11] Sullivan M F, Helbig K. Orthorhombic media modeling elastic wave behavior in vertically fractured earth[J]. Geophysics, 1997, 62(6): 1954-1974.
[12] Hatton L, Larner K L, Gibson B S. Migration of seismic data from inhomogeneous media[J]. Geophysics, 1981, 46(5): 751-767.
[13] Fei T, Larner K. Elimination of numerical dispersion in finite difference modeling and migration by flux corrected transport[J]. Geophysics, 1995, 60(6): 1830-1842.
[14] LIN Xin, Yuan F G. Detection of multiple damages by prestack reverse time migration[J]. American Institute of Aeronautics and Astronautics, 2001, 39(11): 2206--2215.
[15] LIN Xin, Yuan F G. Experimental study applying a migration technique in structural health monitoring[J]. Structural Health Monitoring, 2005, 4(4): 341-353.
[16] 张文生. 波动方程成像方法及其计算[M]. 北京: 科学出版社, 2009: 38-60.
ZHANG Wensheng. The imaging method of wave equation and calculating[M]. Beijing: Science Press, 2009: 38-60.
[17] Zak A, Krawczuk M, Ostachowicz W. Propagation of in plane waves in an isotropic panel with a crack[J]. Finite Elements in Analysis and Design, 2006, 42(1): 929-941.
(编辑 杨幼平)
收稿日期:2012-12-05;修回日期:2013-04-10
基金项目:国家自然科学基金资助项目(50778179)
通信作者:郭少华(1960-),男,陕西西安人,教授,博士生导师,从事结构损伤探测与识别研究;电话:13974814025;E-mail:gsh@csu.edu.cn