J. Cent. South Univ. (2012) 19: 2316-2322
DOI: 10.1007/s11771-012-1277-x
Rheological catastrophic model for soft clays
MA Bo-ning(马伯宁)1, XIE Xin-yu(谢新宇)1, 2, LIU Kai-fu(刘开富)3
1. Key Laboratory of Soft Soils and Geoenvironmental Engineering of Ministry of Education (Zhejiang University),Hangzhou 310027, China;
2. School of Civil Engineering and Architecture, Ningbo Institute of Technology, Zhejiang University,Ningbo 315100, China;
3. Department of Civil Engineering and Architecture, Zhejiang Science and Technology University,Hangzhou 310008, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: A brief review of the former studies on the mechanisms of soil rheology and microstructure is presented. Then a microstructure model and a set of rheological constitutive relations for soft clays, which describe how the rheological consolidation settlement develops, are established in the framework of the catastrophe theory. The validity of this model is verified by a series of rheological consolidation experiments with different loading rates. The experimental data show that creep deformation can be clearly observed in these tests, and the consolidation settlement is loading rate dependent. The characteristics of the deformation can be explained and reproduced successfully using the model. It can be concluded that only the biggest set of voids would collapse for one load increment. Parameters in the model, k and η, are gained by curve fitting. With only two free parameters, good fits of the data are achieved.
Key words: clay; rheological consolidation; microstructure; catastrophic model; oedometer tests
1 Introduction
The consolidation theories are designed to predict the coupled progress of flow and deformation of porous materials, such as clays, under external loads. The excessive pore water pressure dissipates, the effective stress grows as the soil is consolidated, and then the deformation finally tends to be steady. However, in the former works, BUISMAN first discovered the long-term deformation of soils after the excessive pore water pressure is dissipated in experiments, which is also reported in the works of ZEEVAERT [1] and LEONARDS and RAMAIN [2] and also in lots of engineering practices. This long-term deformation which cannot be explained by classic theories is usually called secondary consolidation or creep.
The mechanisms of creep have been studied for decades with a number of different hypotheses. However, there is still no agreement on this topic yet. For instance, TAYLOR et al [3-4] argued that secondary consolidation is a consequence of the restructuring and disturbance caused by shear stress generated in primary consolidation; CASAGRANDE [5] pointed out that secondary consolidation found in laboratory tests is caused by the gradual change of frictional resistance of the experimental apparatus; TAN [6] believed that bonding change of clay particles created creep; POSKITT and BIRDSALL [7] suggested the mechanism of creep as follows: During loading, when the stress reaches the bond strength, a mechanical bond degradation (de-bonding) process is initiated, and the soil structure may fail, which causes the displacement of the clay particles. However, because of the viscosity of the bound water, the clay deforms very slowly, which is recognized as creep. Until nowadays, there is still no consensus on the mechanism of soil creep because of the complicated soil behaviour and the limitations of measuring techniques.
Nonetheless, researches on soil microstructure are vital for the understanding of mechanical behaviour of the clayey soils in engineering practice, for the engineering properties such as permeability. Strength and compressibility ultimately depend on the interaction of soil particles under loading [8-11]. Since 1920s, great progress on the study of soil microstructure has been made because of the advances of the experimental observation and testing techniques. In the early time, GOLDSCHMIDT et al [12], CASAGRANDE [5] and LAMBE [13-14] proposed different formations of fabrics and microstructures of clay. After 1960s, new technologies such as scanning electron microcopy (SEM), X-ray analysis and mercury intrusion porosimetry (MIP) have been used in observing clay materials. These techniques greatly promoted the researches of soil microstructure. TOVEY [15], SMART [16], MITCHELL [11], GILLOTT [17], PUSCH [18-19], BOWLES [9], MORGENSTERN and TCHALENKO [20], COLLINS and McGOWN [21], DELAGE and LEFEBVRE [22] made their significant achievements on this subject. Since 1970s, quantitative analysis of soil microstructure has been raised. One major achievement is that BAZANT et al [23] established the micro-mechanical models of clays and soft rocks, which is a remarkable breakthrough in this area. MIAO et al [24], SHEN [25-26], SUN et al [27] and some other researchers in China also presented their findings in this area.
Based on observations of POSKITT, DELAGE and TAN and other conclusions mentioned above, we made a scheme for studying the rheological consolidation of soft clays from a microscopic view. The arrangement of clay platelets can be seen as a “card house”, built by clay particles of various shapes and sizes bonded with each other [6]. Creep can be accounted for jumping of bonds of clay particles. When the load of clay microstructure reaches its strength, damage occurs, and the structure would fail. In the process of the microstructure collapsing, clay particles rearrange and form more stable and stronger microstructures. In this description of the particle arrangement, it can be seen that the collapse of the individual microstructure unit happens abruptly despite the overall deformation occurs slowly. Thus, we present a catastrophic model that describes such behaviour of clay microstructure unit. It is worth noting that this mechanical model is to depict the characteristics of the clay microstructure and the process of the soil deformation, rather than introducing the deformations of the microstructure in real conditions, especially not that of the individual particles. Therefore, the relationship between the model presented here and the actual rearranging of the clay particles is essentially phenomenological. After that, a set of constitutive relationships which describe the rheological consolidation of clays are developed. Then, one-dimensional consolidation rheological tests are performed to verify this model. Parameters are gained by least square fitting. Finally, some rheological consolidation characteristics are analyzed and reported.
2 Catastrophic model for clay microstructure
The aim of this section is the derivation of a rheological constitutive model suitable to describe the long-term deformation of clayey soil. The derivation contains three steps. First, the physical model simulating the microstructure of the clay is presented, then the failing process of the microstructure model is examined exploiting catastrophe theory, and finally, a set of constitutive relations are derived by analyzing the controlling equations closed by suitable phenomenological models related to the material behavior of the matter.
Bearing all these in mind, we consider the following assumptions on the phenomenological behavior of the system.
2.1 Hypotheses
1) The deformation of the microstructure is completely mechanical;
2) The clay particles are simplified as rigid rods which are hinged together;
3) Kelvin model represents the bonds of the particles, as shown in Fig. 1. The elasto-viscous behaviour of the deformation can be imitated by setting advisable rotational stiffness coefficient k and rotational viscosity coefficient η. The coefficients k and η are related to a number of factors such as mineral composition, cementation, thixotropic hardening, aging, and stress state.
4) The soil deformation is caused by the damage of the microstructure.
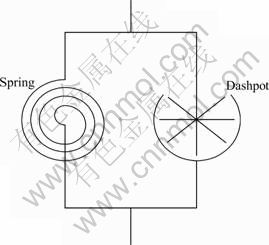
Fig. 1 Jointing model for particles
2.2 Catastrophic model for microstructure
Based on the foregoing hypotheses, we present the microstructure model for clayey soil, as shown in Fig. 2. The whole system stands for the pore structure element of soil. The length of the rods is l. The jointing points of the structure are assumed to be located on a circle of radius 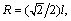 which is the radius of the pore. Denoting the normal stress and the shear stress in the plane where the structure locates is σ and τ, respectively, the normal and tangential components of the load are expressed as
which is the radius of the pore. Denoting the normal stress and the shear stress in the plane where the structure locates is σ and τ, respectively, the normal and tangential components of the load are expressed as
F=σl, S=τl (1)
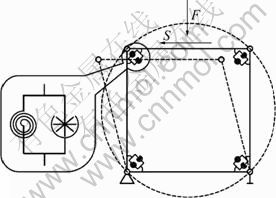
Fig. 2 Microstructural model of clayey soil
Under such load, the deformation of the structure is described by an infinitesimal angle θ in the initial state.
The stress-strain relationship of the Kelvin model is given as
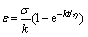 (2)
(2)
As the structure deforms, the deformation energy can be derived as
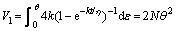 (3)
(3)
where
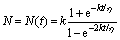 (4)
(4)
The total potential energy can be expressed as
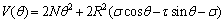 (5)
(5)
According to the theorem of POSTON and STEWART [28], Eq. (5) can be further expressed as
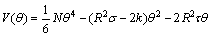 (6)
(6)
which is the standard form of cusp catastrophe. The equilibrium positions satisfy the following relationships:
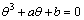 (7)
(7)
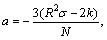
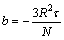 (8)
(8)
where θ is state variable; a and b are control variables. The structure mutates when the following condition is satisfied:
 (9)
(9)
When the stress state of σ and τ satisfies Eq. (9), a relevant radius R can be determined, which identifies the radius of the voids that would fail.
As for the plane stress state, the stress components can be written as
 (10)
(10)
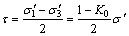 (11)
(11)
where K0 and σ′ denote the effective lateral pressure coefficient and the effective stress, respectively.
Combining Eqs. (9), (10) and (11), the failing criterion of the structure can be obtained as follows:
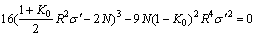 (12)
(12)
The differentiation of Eq. (12) can be expressed as
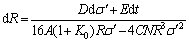 (13)
(13)
where
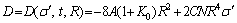
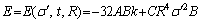
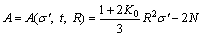
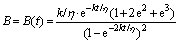
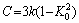
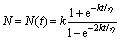
From Eq. (13), it can be seen that if the stress increases by dσ′, the pores of radius between R-dR and R will fail.
2.3 Constitutive relations for creep deformation
When σ and τ satisfy Eq. (9), the solutions of Eq.(6) are
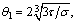
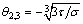 (14)
(14)
Each solution identifies an equilibrium position of the mutating microstructure, indicating that the structure collapse and a new and more stable structure is formed. The sudden change of the angle can be derived as
 (15)
(15)
The initial height of the structure is l, while the height of the newly formed structure is lcosθ. Then the rate of the height change of the microstructure can be written as
 (16)
(16)
The pore distribution of the soil is assumed to be P(R), which satisfies the following relationship:
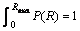 (17)
(17)
If the volume of the void is set as Vpore=1 and the porosity factor is n, obviously the total volume of soil mass is Vtotal=1/n. When the pores of radius between R-dR and R fail, the vertical decrement of the soil mass can be written as
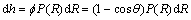 (18)
(18)
The increment of vertical strain is obtained as
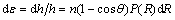 (19)
(19)
where
 (20)
(20)
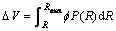 (21)
(21)
where e0 and ΔV denote the initial void ratio and the total volumetric strain, respectively.
Equations (13) and (19) comprise an incremental constitutive model for rheological consolidation. Parameters of the model can be obtained by different ways. e0 can be determined by laboratory soil test and P(R) by the MIP test. Since the effective lateral pressure coefficient K0 varies in the oedometer tests, it is difficult to define the parameter directly. K0 can be obtained as
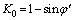 (22)
(22)
In this model, the rotational stiffness coefficient k and the rotational viscosity coefficient η are difficult to obtain in laboratory tests. Therefore, fitting method is used to define the parameters, and their mechanical characteristics are analyzed.
3 Experiments and computation
3.1 Test program
In order to verify the model presented earlier, oedometer tests were performed to observe the mechanical behaviour of clay under long-term loading. The soil investigated in the experiment is Ningbo clay, which is a kind of problematic soil for its low strength, high compressibility and time-dependent behaviour and deposits in Hangzhou Bay, China. The basic properties of the soil are summarized in Table 1. Both moisture content and moist unit weight of this material are significantly less than those of typical natural sedimentary deposits. The soil was cut into replicate specimens with a diameter of 61.8 mm and height of 20.0 mm, and placed in the consolidometer between two porous stones. Table 2 presents the different loading rates used in the experiments. In order to make sure that the creep deformation can be fully developed, each load increment lasts no less than 7 d until the deformation of the specimen is lower than 0.005 mm within 24 h.
Table 1 Properties of testing material
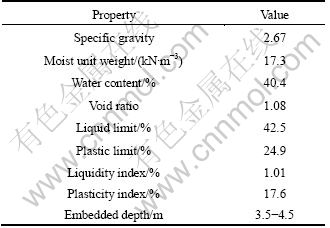
Table 2 Scheme of rheological consolidation tests

3.2 Experiment results and discussion
The experimental results were presented to observe the rheological consolidation behaviour of the clay. The full-process strain versus time of each specimen is illustrated in Fig. 3, in which the rates of strain development attenuate. It is considered that the creep occurs during the whole consolidation process (Hypothesis 2). But the deformation occurs after the dissipation of the excessive pore water pressure can be regarded as creep only, which can be measured easily on the semi-logarithmic coordinate curve. Taking specimen 3 for example, the creep deformation takes 10.5%, 16.2% and 11.1% for each loading increment of the total, which cannot be neglected.
The test results can also be understood from some micromechanical view points. In Fig. 4, the data indicate that the curves of each loading increment can be divided into two parts. The former one is steeper, indicating that the strain increases rapidly with stress, while the latter one is relatively gentle, meaning that the strain increases slowly with stress. This characteristic can be explained by the model that only the class of largest pores will be collapsed for a given consolidation pressure increment. Also, such a conclusion is recognized in the work by DELAGE and LEFEBVRE [22]. As the load increments are applied, the deformation develops rapidly in the early stage, caused by the collapse of inter-aggregate pores that take the majority of the total void volume. As this process goes on, the excessive pore water pressure dissipates, and the deformation continues growing but more tardily because of the viscosity of the bound water, with the particles redistribution and formation of more stable microstructures.
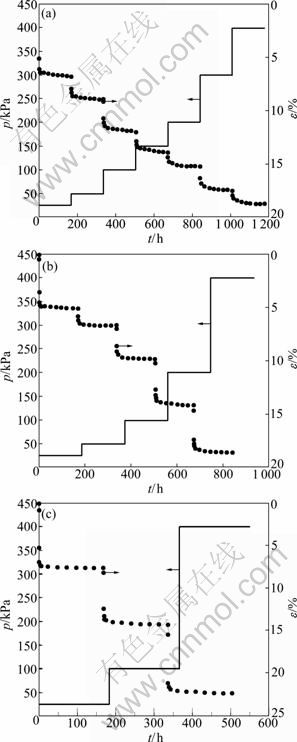
Fig. 3 Full-process strain-time curve: (a) Specimen 1; (b) Specimen 2; (c) Specimen 3
3.3 Computation and curve fitting
Currently, there are a few methods existing in literature to analyze the data of rheological consolidation tests. In the early time, elementary functions were often used for regression analysis, by which the quantitative evaluation and tendency of the creep can be described. However, it is hard to illustrate the mechanical characteristics of the model. Another approach is to transfer the function into a polynomial by Taylor series expansion, then the polynomial is used for curve fitting, by which the parameter of the model can be gained [29-30]. It is worth noting that all these methods assume that the effective stress is constant, which is obviously invalid for the consolidating soil under loads. Thus, we should take into account the increase of the effective stress during consolidation for the model.
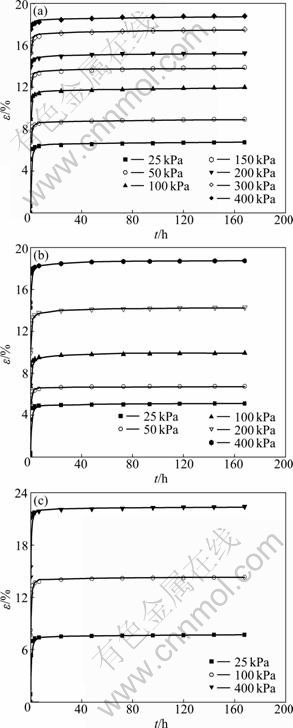
Fig. 4 Comparisons between measured and predicted strain versus time: (a) Specimen 1; (b) Specimen 2; (c) Specimen 3
The analytical solutions to the Kelvin rheological model are adopted here, for the macro-mechanical and the micro-mechanical models can be unified in the same form, and also the solutions are relatively simple. The solutions can be easily achieved by degradation of the solutions to the four-element rheological model [31]. The pore pressure solutions to the Kelvin model can be expresses as
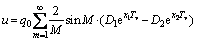 (24)
(24)
where
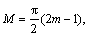 m=1, 2, 3, …
m=1, 2, 3, …
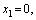
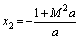 ,
,
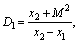

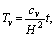
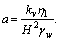
and H is the height of the specimen.
The least squares method is used to obtain k and η by curve fitting. Comparisons between measured and predicted strain versus time of different loading rates for each increment are shown in Fig. 4. Meanwhile, the parameters are presented in Fig. 5.
For comparison purposes, all of the predicted results and the test ones for each specimen are shown respectively. By comparing the experimental data with the calculated curves, it can be seen that there is no big discrepancy between them, despite a little lag of the calculated curves deforms in the early stage. Therefore, the model is proved to be applicable. The test results show that the rheological consolidation is loading rate dependent, which confirms the elasto-viscous behaviour of the clayey soil.
In order to investigate the characteristics of the parameters in the model, the parameters obtained by curve fitting versus consolidation pressure are plotted in Fig. 5. According to the results, k and η vary with the pressure, and the increase of k is roughly linear. By comparing with the specimens of different loading rates, it can be seen that the less the loading rate is, the larger the k becomes. This is probably due to the fact that the specimen of small loading rate endures longer under load, thus the creep could be fully developed, and the soil particles can form stronger structures [8], which leads to a higher value of k.
The parameter η also increases with the pressure. However, the increment is small. The curves indicate that η might be influenced by loading rate and the stress. According to the curves, η of the pervious increments is merely the same and slightly fluctuates. The intersecting and the irregularity of curves are probably due to the disturbance and anisotropy of the samples.

Fig. 5 Variation of parameters k and η: (a) k versus consolidation pressure; (b) η versus consolidation pressure
4 Conclusions
1) According to the understanding of the mechanism of soil creep, a microstructure catastrophic model for soft clays is developed by means of phenomenological methods. The model could be applied to describe the rheological consolidation settlement.
2) A series of rheological consolidation tests of different loading rates are performed. Creep deformation can be clearly observed in these experiments. The data indicate that the mechanical behaviour of the soil can be understood by the feature of pore distribution. Only the biggest set of voids would collapse, causing the rapid growth of deformation in the early stage of each loading increment. There may be some limitations of these one- dimensional tests, yet some conclusions can still be drawn from the test results. Some more sophisticated testing methods might be needed to advance this research in future.
3) The development of strain versus time is established, as well as material parameters versus consolidation pressure. The material parameters are gained by curve fitting. With only two free parameters, good fits of the data are achieved. The variation of both k and η with the pressure are established and converted to the relationship between the loading rate and k. η, apparently, is influenced by more complicated factors.
Acknowledgments
The authors also would like to thank TAO Hai-bing for his help to the computer programming.
References
[1] ZEEVAERT L. Consolidation of Mexico city volcanic clay [C]// Conference on Soils for Engineering Purpose. Philadelphia: ASTM, 1958: 18-32.
[2] LEONARDS G A, RAMIAH B K. Time effects in the consolidation of clays [C]// Symposium on Time Rate of Loading in Testing Soils. Philadelphia: ASTM, 1960: 116-130.
[3] TAYLOR D W. Research on consolidation of clays, Serial 82 [M]. Massachusetts: Massachusetts Institute of Technology, Department of Civil and Sanitary Engineering, 1940: 116-130.
[4] TAYLOR D W, MERCHANT W. A theory of clay consolidation accounting for secondary compression [J]. Journal of Mathematics and Physics, 1940, 3: 167-185.
[5] CASAGRANDE A. The structure of clays and its importance in foundation engineering [J]. Journal of Boston Society of Civil Engineering, Contribution to Soil Mechanics (1925-1940), 1932: 72-125.
[6] TAN T K. Secondary time effects and consolidation of clays [J]. Chinese Journal of Civil Engineering, 1957, 5(1): 1-9. (in Chinese)
[7] POSKITT T J, BIRDSALL R O. A theoretical and experimental investigation of mildly non-linear consolidation behavior in Saturated soil [J]. Canadian Geotechnical Journal, 1971, 8(2): 182- 216.
[8] HOLTZ R D, KOVACS W D. An introduction to geotechnical engineering [M]. Eaglewood Cliffs, NJ: Prentice-Hall, 1981: 197- 374.
[9] BOWLES F A. Microstructure of sediments: Investigation with thin sections [J]. Science 159, 1968. 1236-1237.
[10] BOWLES J E. Physical and geotechnical properties of soils [M]. Auckland: McGraw-Hill, Inc, 1984: 38-43.
[11] MITCHELL J K. Fundamentals of soil behavior [M]. New York: Wiley, 1993: 35-83.
[12] GOLDSCHMIDT V M, BARTH T, LUNDE G. Geochemical distribution law of the elements [M]. Akademi: Skrifer Norskc- Videnskaps, 1926: 89-117.
[13] LAMBE T W. The structure of inorganic soil [C]// Proc Amer Soc Civil Eng, v. 79, separate no. 315, 49. 1953: 1-49.
[14] LAMBE T W. The structure of compacted clay. J. Soil Mech. Found. Div. [C]// Proc Amer Soc Civil Eng, New York: 1958, 84: 1-3.
[15] TOVEY N K. Quantitative analysis of electron micrographs of soil structure [C]// Proceedings of the International Symposium on Soil Structure, Gothenburg, Sweden, 1973: 176-184.
[16] SMART P. Structure of a red clay soil from nyeri, Kenya [J]. Quarterly Journal of Engineering Geology, 1971, 6: 129-139.
[17] GILLOTT J E. Study of the fabric of fine-grained sediments with the scanning electron microscope [J]. Journal of Sedimentary Petrology, 1969, 39: 90-105.
[18] PUSCH R. Quick clay microstructure [J]. Engineering Geology, 1966, 3: 433-443.
[19] PUSCH R. Influence of salinity and organic matter on the formation of clay microstructure [C]// Proc Int Symp Soil Structure, Gothenburg, Sweden, 1973: 161-173.
[20] MOEGENENSTERN N R, TCHALENKO J S. Microscopic structure in kaolin subjected to direct shear [J]. Geotechnique, 1967, 4: 309-328.
[21] COLLINS K, McGOWN A. The form and function of microfabric features in a variety of natural soils [J]. Geotechnique, 1974, 2: 222-254.
[22] DELAGE P, LEFEBVRE G. Study of the structure of a sensitive Champlain clay and its evolution during consolidation [J]. Canadian Geotechnical Journal, 1984, 21: 21-35.
[23] BAZANT Z P, OZAYDIN K, KRIZEK R J. Microplane model for creep of anisotropic clay [J]. Journal of Engineering Mechanics Division, ASCE, 1975, 101(EM1): 57-58.
[24] MIAO Tian-de, LIU Zhong-yu, REN Jiu-sheng. Deformation mechanism and constitutive relation of collapsible loess [J]. Chinese Journal of Geotechnical Engineering, 1999, 21(4): 383-387. (in Chinese)
[25] SHEN Zhu-jiang. A masonry model for structured clays [J]. Rock and Soil Mechanics, 2000, 21(1): 1-4. (in Chinese)
[26] SHEN Zhu-jiang. An elasto-plastic damage model for cemented clays [J]. Chinese Journal of Geotechnical Engineering, 1993, 15(3): 1-6. (in Chinese)
[27] SUN Qiang, ZHANG Xiao-ke, LI Hou-en. Research on microstructural catastrophe model of deformation of collapsible loess [J]. Rock and Soil Mechanics, 2008, 29(3): 663-667. (in Chinese)
[28] POSTON T, STEWART I N. Catastrophe theory and its applications [M]. London: Pitman, 1978: 123-171.
[29] DRAPER N R, SMITH H. Applied regression analysis [M]. New York: Wiley, 1981: 600-686.
[30] XU H F, QIAN Q H, WU H J, CHEN W. A polynomial regressive inverse method to determine rheological parameters of soft soil [J]. Chinese Journal of Geotechnical Engineering, 2003(3): 365-367.
[31] XIE K H, XIE X Y, LI X B. Analytical theory for one-dimensional consolidation of clayey soils exhibiting rheological characteristics under time-dependent loading [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32: 1833-1855.
(Edited by HE Yun-bin)
Foundation item: Project(51079126) supported by the National Natural Science Foundation of China; Project(Y1090971) supported by the Natural Science Foundation of Zhejiang Province, China
Received date: 2011-06-10; Accepted date: 2011-10-16
Corresponding author: XIE Xin-yu, Professor, PhD; Tel: +86-13336016368; E-mail: xiexinyu@zju.edu.cn