Numerical simulation on behavior of pile foundations under cyclic axial loads
来源期刊:中南大学学报(英文版)2017年第12期
论文作者:衡帅 ZHAO Ming-hua(赵明华) 郑玥
文章页码:2906 - 2913
Key words:pile foundation; ABAQUS; cyclic dynamic load; numerical simulation; pile-soil interaction; secondary development
Abstract: On the basis of the two dimensional finite element analysis model, the pile foundations’ mechanical effect of the rigid pile composite foundation under the dynamic load was researched. Through the research, the development law and deformation property of axial force of pile body, shaft resistance of pile, and cumulative settlement of pile head under vertical cyclic dynamic loads were concluded. Through the comparison and analysis of the test results of dynamic models, the test results of Poulos (1989) and cumulative settlement model of the single pile under cyclic loads were confirmed. Based on the above research, Fortran language was adopted to introduce the soil attenuation factor, the secondary development of relevant modules of ABAQUS was carried out, and the effect of soil attenuation factor on dynamic property of pile-soil was discussed further.
Cite this article as: ZHAO Ming-hua, HENG Shuai, ZHENG Yue. Numerical simulation on behavior of pile foundations under cyclic axial loads [J]. Journal of Central South University, 2017, 24(12): 2906–2913. DOI:https://doi.org/10.1007/s11771-017-3704-5.
J. Cent. South Univ. (2017) 24: 2906-2913
DOI: https://doi.org/10.1007/s11771-017-3704-5
ZHAO Ming-hua(赵明华), HENG Shuai(衡帅), ZHENG Yue(郑玥)
Institute of Geotechnical Engineering, Hunan University, Changsha 410082, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Abstract: On the basis of the two dimensional finite element analysis model, the pile foundations’ mechanical effect of the rigid pile composite foundation under the dynamic load was researched. Through the research, the development law and deformation property of axial force of pile body, shaft resistance of pile, and cumulative settlement of pile head under vertical cyclic dynamic loads were concluded. Through the comparison and analysis of the test results of dynamic models, the test results of Poulos (1989) and cumulative settlement model of the single pile under cyclic loads were confirmed. Based on the above research, Fortran language was adopted to introduce the soil attenuation factor, the secondary development of relevant modules of ABAQUS was carried out, and the effect of soil attenuation factor on dynamic property of pile-soil was discussed further.
Key words: pile foundation; ABAQUS; cyclic dynamic load; numerical simulation; pile-soil interaction; secondary development
1 Introduction
The bearing capacity analysis and settlement calculation of rigid pile composite foundations under embankment loads are hot issues in the field of geotechnical engineering, whose relevant theoretical study is becoming mature and gradually applied in engineering practice. It is worth noting that most of the theoretical analyses assume that embankment loads are static loads, and the dynamic properties of traffic moving loads are not considered fully. Obviously, during the operation period, the rigid pile composite foundation of expressway embankment should bear not only the dead load generated by the embankment deadweight, but also the cyclic dynamic loads of the periodic vehicle driving. As a result, the research of soil dynamic properties and interaction mechanism of pile-soil under the premise of cyclic dynamic loads will be another key to research the bearing capacity and settlement calculation of the rigid pile composite foundation under traffic moving loads. Under the long-term dynamic loads, the deformation property of soil appears as accumulated deformation mainly. Scholars put forward computational and empirical expressions of all kinds of accumulated deformations specifically through the cyclic triaxial test and the research of model test. The representative achievements include: the traditional index model through indoor model tests based on the consideration of the effect of dynamic strength of soil has been improved [1]; on this basis, the effect of initial stress field has been taken into consideration [2]; the effect of the residual stress on the soil accumulated deformation has been analyzed in detail [3]; the semilogarithm relationship between attenuation index and cycle times has been proposed [4]; CHEN et al [5] systematically researched the bearing and deformation behavior of the rigid pile of saturated silt foundation through a series of large scale model tests; POULOS [6, 7] made a series of theoretical researches and experimental investigations about the cyclic weakening property of bearing capacity of pile foundations, and established the empirical formula of the attenuation of bearing capacity along with cycles of axial loads; a series of 1 g model tests to research the long- term mechanical behavior of marine fan foundation in saturated soft clay foundation under cyclic loads have been made, which discovered that after the dynamic load, the soil around pile weakened obviously [8]. The numerical software is adopted to simulate the actual working conditions of the pile foundation under embankment. Under the action of vertical cyclic loading, the pile foundation attends to the attenuation of the bearing capacity and stiffness and increasingly forms cumulative settlement [9–11]. After the comparison with the results of dynamic model test, its accuracy was verified, and then, the second development platform of ABAQUS was used to introduce the soil attenuation factor. The relationships between the attenuation factor and cycle times were assumed to appear as the hyperbolic function, and the effect of attenuation factor on soil’s dynamic law and settlement property was analyzed further.
2 Dynamic model parameters of pile
2.1 Vertical loaded pile under undrained conditions
Considering that the concrete solid circular pile is located in the normally consolidated saturated clay, the groundwater level is parallel to the foundation. The pile length is 10 m, and the pile diameter is 0.5 m with vertical cyclic loading. Considering the axial symmetry, the axisymmetric model is adopted to analyze. In order to minimize the effect of boundaries on analysis regions, the pile tip of analysis region should extend downward to the length of a pile, and the horizontal length should be 20 times the pile diameter. The pile body adopts linear elasticity model with elasticity modulus of 20 GPa, Poisson ratio of 0.2, unit weight of 25 kN/m3, pile–soil interface friction angle of 25°. The foundation soil body is saturated and underground water level is leveled with ground water level and drainage water analysis is applied in the program. Mohr–Coulomb elastic-plastic model is applied in the simulation with calculation parameters shown in Table 1.
Table 1 Physical and mechanical properties of clay

2.2 Establishment and solution of model
The general finite element software ABAQUS is adopted to establish the above model. The major steps are as follows:
1) Establish the pile and the soil part, then set material parameters and section properties;
2) Define and analyze the step and the interaction type;
3) Define the load and the boundary conditions;
4) Divide the mesh, submit the job, and conduct the visualization.
An analysis is conducted on a concrete solid circular pile of the saturated-clay foundation as an example. In the model, the diameter of the pile is 0.5 m, and the length of the pile is 10 m when the analysis region of the foundation modeling is 10 m in breadth and 20 m in depth. With the axial symmetry model taken into consideration, both sides of the model are constrained by horizontal direction and bottom of the model by both horizontal and vertical directions. Interface unit is set on pile–soil interface to perform simulation. The model adopts quadrilateral solid elements with serendipity, which are divided into 2000 units. Radial mesh division (single bias) is applied with bias ratio to be 5. Within soil-body interface region of the pile body, both displacement and stress vary greatly, thereby, mesh with greater density is needed to enhance computing accuracy. Figures 1 and 2 show single-pile finite element analysis model and mesh subdivision sketch map respectively.

Fig. 1 Single-pite finite element analysis part
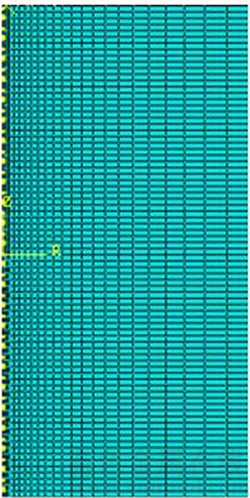
Fig. 2 Single-pite finite element analysis mesh
2.3 Analysis of initial conditions
The reasonable setting of the initial stress is extremely important for the reliability of solution.
Initial stress field, used to confirm initial stress conditions of pile body and foundation soil body, determines distribution and value of horizontal lateral pressure of the pile body. Initial stress field also determines distribution law of soil strength in foundation in terms of Mohr–Coulomb model. Therefore, the reasonable setting of initial stress is of vital importance to finite element analysis of geotechnical engineering. In terms of pile foundation, generally speaking, its mature initial normal stress is supposed to be equal to earth pressure at rest, meaning that in the equation:
 (1)
(1)
where K0 is the coefficient of initial horizontal earth pressure, which can be received from
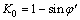 (2)
(2)
Ground stress field is generally caused by self-weight of soil body in vertical direction. However, direct gravity load on finite element analysis will lead to two types of problems:
1) The gravity load exerted on it will cause greater soil deformation, which is supposed to form at the formation stage of foundation instead of forming in the calculation.
2) The interaction between soil body and pile body caused by foundation deformation does not agree with practice situation. Therefore, an equilibrium test of ground stress is a must before the finite element analysis.
It is convenient to set initial ground stress in ABAQUS. The value and distribution of ground stress can be set directly by module of “initial conditions”, and then, balance computation of ground stress will be automatically conducted through the program to ensure that the initial displacement of pile-soil system is zero.
2.4 Definition of cyclic loading
The loading methods of dynamic loads are divided into force-controlled cyclic loading and displacement- controlled load cycles. The latter is adopted in this work. Cyclic load ratio is the extremely important parameter to research the dynamic property of pile-soil for dynamic model test, and the load ratio is decided by two factors primarily: amplitude of vertical cyclic loads and ultimate bearing capacity of the pile foundation. The adoption of displacement-controlled cyclic loads can not only compare and verify the results of numerical simulation and model test, but also compare the effect of pile foundation under force-controlled cyclic loads and displacement-controlled cyclic loads. The expression of vertical cyclic loading is as follows:
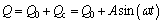 (3)
(3)
According to the formula, the cyclic loading of downward pressure consists of two parts, dead load Q0 and cyclic load Qc. For the convenience of discussion, the initial vertical and downward-pressure dead load amplitude Q0 is 25 cm and the vertical and downward- pressure cyclic load amplitude A is at most 25 cm. In this text, comparative analysis of six groups of different cyclic dynamic load amplitudes is carried on when A is equal to 25, 20, 15, 10, 5 and 1 mm, respectively.
3 Analysis of parameters
3.1 Loading features of pile foundation when monotony cycle is loading
Influenced by the vertical load, soil body of both pile lateral and pile tip share the pile-top load: some load is transferred to soil body of pile lateral by the interaction of interface between pile and soil in the form of shear stress and other load to the bearing stratum of pile tip via pile tip. During the transmission of axial load, uneven distribution of axial force generates along the pile body due to the function of shaft resistance of pile. In light of compressibility of pile body material, compressive deformation of pie body produces to a certain extent. On the other hand, soil body from pile tip undergoes compressive deformation to a certain extent by common effect of pile-tip load and transferring downward load of shaft resistance of pile. The aforementioned causes the sedimentation deformation of pile top under vertical loading. Thus, it can be seen that the bearing and deformation of pile foundation under vertical loading, a result of interaction of pile-soil, which varies according to the size of pile foundation, material property, soil body features of pile lateral and pile tip, load and so forth, are a process of extremely complicated interaction.
3.2 Development law of cumulative settlement of pile head
Just as shown in Fig. 3, to analyze the development law of cumulative settlement, we define the load with dead load of 25 cm and cyclic load of 25 cm too while the frequency is 1 Hz.
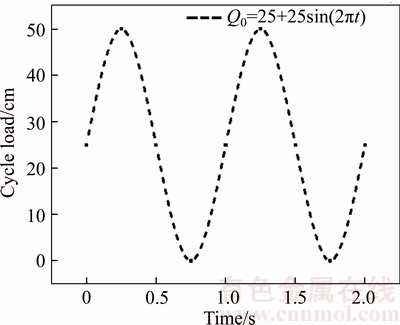
Fig. 3 Defined cyclic load
Figure 4 suggests that when the vibration period is comparatively small (when N<12000 in the graph), the cumulative settlement of pile head will develop quickly, and the settlement of pile head will have a linear variation along with the vibration period. Thus, it can be seen that smaller vibration periods of load are not able to make the pile reach its ultimate bearing capacity. By contrast, it is observed that the settlement rate of pile head will decrease and flatten out gradually with the constant increase of vibration period, which suggests that at the moment the pile-soil is intensified.
As a result, to embody the effect of vibration period on the settlement of pile head, the parameter of vibration period N=1000 is adopted as the standard to analyze the dynamic property of pile-soil under cyclic loads. In this graph, it is the linear variation stage of the cumulative settlement of pile head.
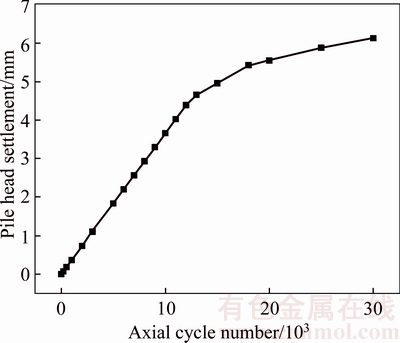
Fig. 4 Cumulative settlement of pile head
3.3 Confirmation of analog frequency of cyclic dynamic loads
The exciting frequency is adopted to simulate the effect of vehicle speed of rapid transit. The excitation frequency which is exerted on the structure increases with the increase of vehicle speed. It can be approximatively calculated according to the following formula:
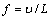 (4)
(4)
where L is the vehicle length, and υ is the vehicle speed.
The field data suggest that the load frequency of the pile foundation is comparatively low, which usually does not exceed 6 Hz [12]. That is because the pile-soil has a vibration natural frequency, when the load frequency is comparatively high and approaches the vibration natural frequency of pile-soil, the pile-soil will become unstable and is likely to be destroyed. As a result, most of the dynamic model tests adopt comparatively low frequency in order to make the analysis results of pile-soil dynamic properties more stable. In order to analyze the effect of cyclic load frequency on failure mechanism of pile-soil effect, six groups of frequency parameters: f=1, f=2, f=3, f=4, f=5 and f=6 Hz are adopted in this work. It can be seen from Fig. 5 that when f<4 Hz, the curve of displacement and the curve of settlement will almost coincide, which suggests that the effect of low frequency on the effective stress of pile section turns out to be small. However, when the frequency of cyclic dynamic load is 5 Hz or 6 Hz, the section stress of pile will change suddenly, and the pile-soil is unstable at the moment. As a result, in order to simulate the dynamic property and settlement law of pile-soil under cyclic dynamic loads accurately, this work uniformly adopts the frequency parameter f=1 Hz to simulate the underdraught cyclic dynamic load.
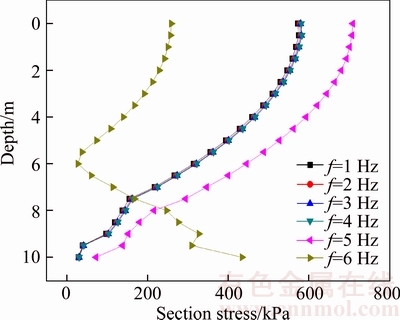
Fig. 5 Section stress under different frequencies
3.4 Effect of amplitude of cyclic dynamic loads on axial force of foundation pile
Under the effect of the displacement-controlled cyclic load, the curve of the axial force of pile head is shown in the graph. When the cyclic displacement amplitudes of the load cycle are 25 mm and 20 mm, the pile head’s axial force Pmax will decrease in a certain decreasing rate with the increase of cycle times.Figures 6 and 7 show that during the previous 10 cycle periods, the attenuation of axial force of pile body is obvious, which is the same as the conclusion of POULOS [6, 7].
The reduction of Pmax mainly derives from the loss of pile shaft friction. When the pile is subjected to cyclic axial loads, the pile shaft friction reduces due to a decrease in the normal stress caused by cumulative contraction of the soil within the shear zone close to the pile-soil interface [13, 14]. In each load cycle, although dilation occurs in the shear zone firstly, the shear band contracts significantly after revesal of the loading direction, leading to some net contraction per cycle.
For the pile, Pmax rose to around 130.8 kN at a settlement of 20 mm in the first cycle, and decreased to 114 kN after 10 cycles; while the pile was around 162 kN in the first cycle and reduced to 122 kN after 10 cycles with an amplitude of 25 mm. For piles at different amplitudes of 20 mm and 25 mm, Pmax decreased to around 112 kN after 100 cycles. Although this Pmax value of pile at a settlement of 25 mm is 1.2 times that found using an amplitude of 20 mm in the first cycle, it then decreased much more significantly and became comparable to that found using an amplitude of 20 mm after 10 cycles. Thus, the reduction in Pmax increases with increasing amplitude of cyclic load, indicating that the reduction in radial stress in the soil increases rapidly with increasing amplitude of a cyclic displacement. However, the ultimate mobilized radial stresses of soil surrounding the pile shaft are similar and tend to a stable value for different cyclic displacement amplitudes [15–17].

Fig. 6 Axial force of pile body when cyclic load amplitude A=20 mm

Fig. 7 Axial force of pile body when cyclic displacement amplitude A=25 mm
3.5 Effect of amplitude of cyclic dynamic loads on settlement of pile body
It can be seen from Fig. 8 that with the increase of dynamic load amplitude, the settlement of pile body will increase gradually with the increase of depth, and the settlement of pile head is bigger than the settlement of pile tip. The reason is that not only the pile subsides vertically, but also the material compresses and deforms to some degree under the effect of cyclic loads. In order to reflect the effect of dynamic load amplitude on pile settlement more clearly, the cumulative settlement of pile head is adopted to analyze, and Fig. 8 of the changing relation between cumulative settlement of pile head and cycle times N is drawn.
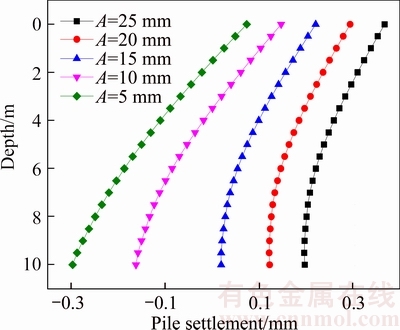
Fig. 8 Settlement of pile body of different cyclic displacement amplitudes
Under the condition of continuous gradual loading, different cyclic displacement amplitudes will have a certain effect on the cumulative settlement of pile head, as shown in Fig. 6. The cumulative settlement of pile head appears as a linear growth with the increase of cycle times, and the bigger the amplitude is, the bigger the cumulative settlement of pile head under the identical cycle times is, which is the same as the results of the model test research of ZHU et al [18].
In addition, it can be seen from Fig. 9 that the negative settlement will appear when the cyclic load amplitude exerted from above is comparatively small. The reason is that a 25 mm underdraught displacement was exerted to the concrete pile in advance before the exertion of cyclic dynamic loads, thus the displacement direction of load will keep downward all along in the working process of cyclic dynamic loads. The expression of the upper cyclic load is: Q=Q0+Asin(ωt), the Q0 is advance underdraught displacement, and 25 mm of the displacement is adopted in this work. A is the amplitude of cyclic dynamic loads, and ω is the frequency of cyclic dynamic loads. Pressing the pile in advance will cause rebound displacement, which means that when the cyclic dynamic load is exerted from above, the pile will move upwards instead. To research and analyze the phenomenon, 6 groups of cyclic dynamic load’s amplitudes (A=25, A=20, A=15, A=10, A=5, A=1 mm) are adopted, and the results are shown in Fig. 10. It can be seen from the graph that when the amplitude of upper cyclic dynamic load is comparatively small, the rebound displacement will be comparatively obvious. This is because the smaller cyclic load is not able to stop the rebound tendency of the pile, and the settlement caused by the cyclic dynamic load is smaller than the rebound displacement, thus the ultimate settlement will manifest as negative settlement. As a result, the rebound displacement of pile will gradually decrease with the increase of the amplitude of cyclic dynamic loads.
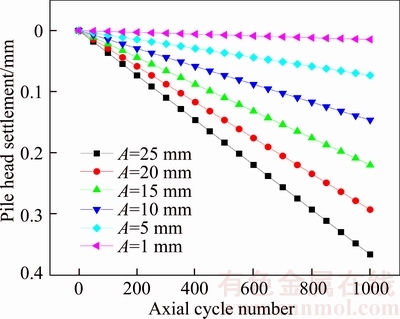
Fig. 9 Cumulative settlement of pile head of different cyclic displacement amplitudes
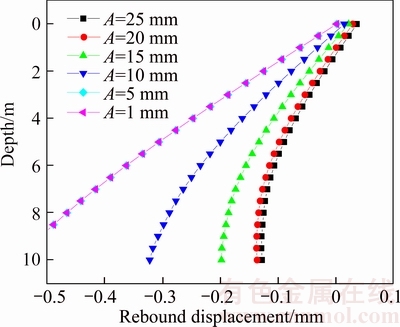
Fig. 10 Rebound displacement of pile of different cyclic displacement amplitudes
4 Secondary development of ABAQUS
4.1 Purposes of secondary development
Though ABAQUS provides a great deal of cell libraries and resolution models, enabling users to address a majority of problems, it is impossible for ABAQUS to directly solve all the potential problems and to present all constitutive models, due to the extreme complicity of practical issues and mushroom growth of constitutive models and corresponding algorithms. As a result, ABAQUS offers a mass of user subroutines to allow users to define their own models and units that accord with specific problems when they fail to find appropriate models or units. These user subroutines include modeling, material, load and each part of the unit, which are conductive to the application of ABAQUS in the analysis of practical projects.
4.2 Secondary development platform of ABAQUS
The secondary development of ABAQUS is able to simulate extremely complex working condition, and its reliability of calculation has been approved widely. The secondary development platform provided by ABAQUS is adopted to put the module of soil attenuation factor into ABAQUS. The main interface program related to this exploitation is the material user-defined programs UMAT. ABAQUS provides users with UMAT as the Fortran program interface to define their own material properties. The material database of ABAQUS does not define the material model which attenuates with the exterior load, so we need to adopt the user material subroutine (UMAT) and the interface of the main solver of ABAQUS to implement the attenuation of the soil. In the input file, the key word “*USER MATERIAL” is used to express the definition of user’s material properties. The key variables related to the development process are:
1) The variables are from the interface:
STRAN(NTENS): the strain matrix when the increment step begins; NTENS refers to the number of stress components or strain components.
DSTRAN(NTENS): incremental strain matrix.
PROPS(NPROPS): the array of material parameters defined by users; It refers to the number of material parameters, which is confirmed by the key word constants of *user material* in the input file of ABAQUS.
2) The variables need to be updated by users:
DDSDDE(NTENS,NTENS): jacobian matrix, which has an important effect on the solution of convergence speed. However, DDSDDE does not affect the ultimate effect of convergence’s solution.
STRESS(NTENS): stress matrix. When the increment step begins, the UMAT will be input, and when the increment step ends, the UMAT needs to be updated and sent to another increment step by users.
This work assumes that the soil attenuation is only related to axial cycle numbers, and if the effect of properties and depth of soil is not considered, the relationship between soil attenuation factor and cycle times is shown as the following hyperbolic function [19, 20]:
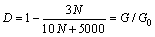 (5)
(5)
which is based on the previous experimental data and the attenuation. In the formula, N refers to the cycle times, and G0 refers to the initial shear stiffness of soil.
The accuracy of the numerical simulation in this work is verified through the comparison with the results of dynamic model test; in the practical rapid transit engineering, the shear stiffness and shear modulus of soil are not constants, and they are affected by many factors, including soil properties, loading rate, cyclic displacement amplitude, and period, etc. However, it is difficult for the module of ABAQUS to simulate the condition of attenuation; as a result, in order to consider the soil attenuation under cyclic dynamic loads, Fortran language is programmed to define the above modules of attenuation factor, and then put them into ABAQUS to research the effect of soil attenuation factor on axial force of pile, shaft resistance of pile, and settlement of soil.
4.3 Comparison of shaft resistance of pile
It can be seen from Fig. 11 that before and after the introduction of attenuation factor, the shaft resistance of pile increases with the increase of depth in the plastic zones, and reaches the peak finally; when the depth increases to the elastic zone, the shaft resistance of pile begins to decrease; when it reaches the pile bottom, the friction resistance is almost eliminated totally, and the global regularity of the two remains the same. However, after the consideration of attenuation factor, the decreasing degree of shaft resistance of pile in elastic zones is more obvious. In other words, considering the attenuation factor, the curve of shaft resistance of pile changes more obviously after the peak.

Fig. 11 Comparison of shaft resistance of pile before and after introduction of attenuation factor
4.4 Comparison of axial force of pile body
It can be seen from Fig. 12 that under the effect of the identical cycle period, the effect of soil attenuation on the variation law of axial force in the upper plastic zone of the pile is low, and its effect on the axial force at the same depth decreases slightly. However, in the lower elastic zone, the effect of soil attenuation makes the axial force of pile body increase obviously. The reason is that the shaft resistance of pile in the elastic zone decreases, and the vertical load of pile increases relatively after the consideration of the attenuation factor.
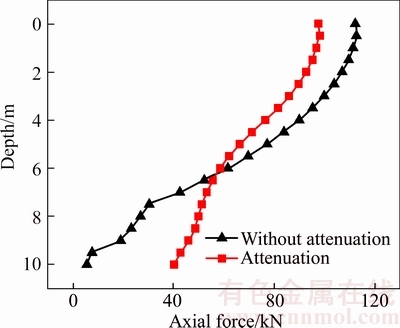
Fig. 12 Comparison of axial force of pile body before and after introduction of attenuation factor
4.5 Comparison of cumulative settlement of pile head
Considering the effect of soil attenuation factor, the cumulative settlement displacement of pile head also changes. In Fig. 13, the pile head is used as the analytical point to research the variation of the cumulative settlement displacement of pile with the variation of attenuation factor. It can be seen from Fig. 13 that the increasing rate of cumulative settlement displacement of pile head after the consideration of soil attenuation is bigger than the rate without the consideration of the attenuation with the increase of cycle times, which is the same as the variation law in the practical engineering.
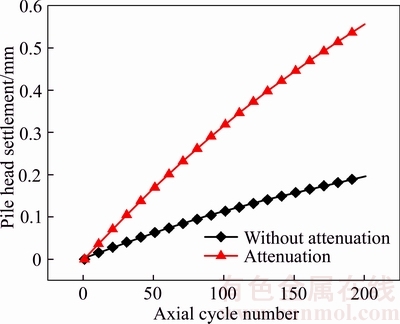
Fig. 13 Comparison of cumulative settlement of pile head before and after introduction of attenuation factor
5 Conclusions
1) When the numerical simulation method is adopted to simulate the mechanical effect of pile foundation under cyclic dynamic loads, it can be seen that the decreasing amplitude of the development law of axial force is the biggest during the previous 10 cycle periods, and the ultimate radial stress of pile lateral is similar for different cyclic displacement amplitudes.
2) In the view of cumulative settlement of pile head, the cumulative settlement basically shows linear growth with the cycle times under the effect of different cyclic displacement amplitudes, and the bigger the amplitude is, the bigger the cumulative settlement of pile head under identical cycle times is.
3) The second development platform of ABAQUS is adopted to lead in the module of soil attenuation factor; the results indicate that the soil attenuation has a certain effect on axial force of pile body, shaft resistance of pile, and cumulative settlement of pile head. Considering the attenuation the soil suffers from, cumulative settlement of pile head, the axial force in the elastic zone of pile and the axial force increase as the shaft resistance of pile decreases under the same cycle times; however, the soil attenuation has little effect on the axial force and shaft resistance of pile in the plastic zone.
References
[1] LI D Q, SELIG E T. Cumulative plastic deformation for fine-grained subgrade soils [J]. Journal of Geotechnical Engineering, 1996, 122(12): 1006–1013.
[2] CHAI J C, MIURA N. Traffic-load-induced permanent deformation of road on soft subsoil [J]. Journal of Geotechnical & Geoenvironmental Engineering, 2002, 128(11): 907–916.
[3] ABDELKRIM M, BONNET G, BUHAN P D. A computational procedure for predicting the long term residual settlement of a platform induced by repeated traffic loading [J]. Computers & Geotechnics, 2003, 30(6): 463–476.
[4] YASUHARA K, YAMANOUCHI T, HIRAO K. Cyclic strength and deformation of normally consolidated clay [J]. Soils & Foundations, 1982, 22(3): 77–91.
[5] CHEN Ren-peng, REN Yu, CHEN Yun-min. Experimental investigation on single stiff pile with long-term axial dynamic loading [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12): 1926–1933. (in Chinese)
[6] POULOS H G. Cyclic stability diagram for axially loaded piles [J]. ASCE, 1988: 877–895.
[7] POULOS H G. Cyclic axial loading analysis of piles in sand [J]. Journal of Geotechnical Engineering, 1989, 115(6): 836–852.
[8] LOMBARDI D, BHATTACHARYA S, WOOD D M. Dynamic soil–structure interaction of monopile supported wind turbines in cohesive soil [J]. Soil Dynamics & Earthquake Engineering, 2013, 49(8): 165–180.
[9] CHAN S F, HANNA T H. Repeated loading on single piles in sand [J]. Journal of the Geotechnical Engineering Division, 1980, 106(2): 171–188.
[10] AL-DOURI R H, POULOS H G. Predicted and observed cyclic performance of piles in calcareous sand [J]. Journal of Geotechnical Engineering, 1995, 121(1): 1–16.
[11] BRIAUD J L, FELIO G Y. Cyclic axial loads on piles: Analysis of existing data [J]. Canadian Geotechnical Journal, 2011, 23(3): 362–371.
[12] PENG Xiong-zhi, ZHAO Shan-rui, LUO Shu-xue, WANG Ai-ling. Dynamic model tests on pile foundation of high-speed railway bridge [J]. Chinese Journal of Geotechnical Engineering, 2002, 24(2): 218–221. (in Chinese)
[13] WHITE D J, LEHANE B M. Friction fatigue on displacement piles in sand [J]. Geotechnique, 2004, 54(10): 645–658.
[14] WHITE D J, DEEKS A D. Recent research into the behavior of jacked foundation piles [C]// Proceedings of International Workshop on Recent Advances in Deep Foundation. The Netherlands, 2007, 25(10): 151–154.
[15] CHEN Ding. Analysis of dynamic response for the influence of high speed railway [D]. Changsha: Central South University, 2010. (in Chinese)
[16] LI Z, HAIGH S, BOLTON M. The behavior of a single pile under cyclic axial loads [J]. Deep Foundations and Geotechnical In Situ Testing, 2010, 78(9): 143–148.
[17] L Wen-tian. Study on dynamical characteristics of the railway bridge pile foundation under static-dynamic load [D]. Changsha: Central South University, 2005. (in Chinese)
Wen-tian. Study on dynamical characteristics of the railway bridge pile foundation under static-dynamic load [D]. Changsha: Central South University, 2005. (in Chinese)
[18] ZHU Bin, REN Yu, CHEN Ren-peng, CHEN Yun-min, WANG Zhen-yu. Model test on bearing capacity and accumulated settlement of single pile subjected to axial cyclic loading [J]. Chinese Journal of Geotechnical Engineering, 2009, 31(2): 186–193. (in Chinese)
[19] BAI Li-dong. Effects of loading history on maximum shear modulus of sand by resonant column tests [J]. Chinese Journal of Rock Mechanics and Engineering, 2011(11): 2366–2374. (in Chinese)
[20] XU Yi-qing, TANG Yi-qun, REN Xing-wei, WANG Yuan-dong, YE Gui-ming. Experimental study on dynamic elastic modulus of reinforced soft clay around subway tunnel under vibration loading [J]. Engineering Mechanics, 2012(7): 250–255. (in Chinese)
(Edited by HE Yun-bin)
Cite this article as: ZHAO Ming-hua, HENG Shuai, ZHENG Yue. Numerical simulation on behavior of pile foundations under cyclic axial loads [J]. Journal of Central South University, 2017, 24(12): 2906–2913. DOI:https://doi.org/10.1007/s11771-017-3704-5.
Foundation item: Projects(51478178, 51508181) supported by the National Natural Science Foundation of China
Received date: 2016-03-03; Accepted date: 2016-07-15
Corresponding author: HENG Shuai; Tel: +86–18373177348; E-mail:2473137935@qq.com

