DOI: 10.11817/j.issn.1672-7207.2017.03.006
Mn-Ni-Mo系核电用钢高温流变行为及热加工图
王梦寒,王根田,王瑞,孟烈
(重庆大学 材料科学与工程学院,重庆,400044)
摘要:在变形温度为950~1 250 ℃、变形速率为0.01~10 s-1的条件下对Mn-Ni-Mo系核电用钢进行高温热压缩实验。结合Arrhenius双曲正弦本构方程,通过多元线性回归分析获得热激活能Q、结构因子A及材料常数n和α对应变的响应规律,从而建立流变应力与应变量、温度和应变速率之间的变参数Arrhenius本构模型。同时,基于真应力-应变曲线,建立输入参数为温度(T)、变形速率( )、应变(
)、应变( )和输出参数为流变应力(
)和输出参数为流变应力(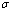 )的神经网络预测模型(ANN)。研究结果表明:神经网络模型(ANN)的预测精度更高,其预测流变应力的平均相对误差为1.31%。根据动态材料模型理论(DMM),构建并分析合金在应变为0.9时的热加工图,确定了最佳热变形工艺参数,即当变形温度为950~1 250 ℃,应变速率为0.06~0.3 s-1时,峰值功率耗散系数(
)的神经网络预测模型(ANN)。研究结果表明:神经网络模型(ANN)的预测精度更高,其预测流变应力的平均相对误差为1.31%。根据动态材料模型理论(DMM),构建并分析合金在应变为0.9时的热加工图,确定了最佳热变形工艺参数,即当变形温度为950~1 250 ℃,应变速率为0.06~0.3 s-1时,峰值功率耗散系数(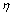 )约为0.54;当变形温度为1 100~1 250 ℃,应变速率为0.3~1 s-1时,峰值功率耗散系数(
)约为0.54;当变形温度为1 100~1 250 ℃,应变速率为0.3~1 s-1时,峰值功率耗散系数(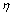 )约为0.44。
)约为0.44。
关键词:Mn-Ni-Mo系核电钢;本构模型;神经网络;热加工图
中图分类号:TG146.2 文献标志码:A 文章编号:1672-7207(2017)03-0592-09
Hot deformation and processing map of Mn-Ni-Mo system nuclear power steel
WANG Menghan, WANG Gentian, WANG Rui, MENG Lie
(College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China)
Abstract: The hot deformation behavior of Mn-Ni-Mo system nuclear power steel was conducted at 950-1 250 ℃ and strain rates of 0.01-10 s-1. Combining Arrhenius hyperbolic sine constitutive equation, the response mechanism of activation energy Q, structural factor A, materials constants n and α on the strain were obtained through multiple linear regression analysis, and the Arrhenius model of flow stress with variable parameters was established. At the same time, the artificial neural network (ANN) model was developed based on the true stress-strain curves, where the inputs parameters were deformation temperature (T), strain rate ( ), strain (
), strain ( ), and flow stress (
), and flow stress (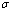 ) was the output parameter. The results show that the ANN model is more accurate in predicting the flow stress, and the average relative error is 2.53%. Based on the dynamic material model (DMM), the processing map of the studied alloy at strain 0.9 is constructed to recognize optimum hot deformation process parameters: deformation temperate ranges of 950-1 250 ℃ and strain rates of 0.06-0.3 s-1 with a peak power dissipate efficiency (
) was the output parameter. The results show that the ANN model is more accurate in predicting the flow stress, and the average relative error is 2.53%. Based on the dynamic material model (DMM), the processing map of the studied alloy at strain 0.9 is constructed to recognize optimum hot deformation process parameters: deformation temperate ranges of 950-1 250 ℃ and strain rates of 0.06-0.3 s-1 with a peak power dissipate efficiency (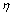 ) of about 0.54, deformation temperate ranges of 1 100-1 250 ℃ and strain rates of 0.3-1 s-1 with a peak power dissipate efficiency (
) of about 0.54, deformation temperate ranges of 1 100-1 250 ℃ and strain rates of 0.3-1 s-1 with a peak power dissipate efficiency (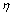 ) of about 0.44.
) of about 0.44.
Key words: Mn-Ni-Mo system nuclear power steel; constitutive model; artificial neural network; hot processing map
随着世界各国对能源需求量的急剧增加,核电逐渐成为重要的能源工业,而反应堆压力容器(reactor pressure vessel, RPV)被称为核电站最关键的组件之一[1-2]。目前,Mn-Ni-Mo系低碳合金钢(ASME SA508-3)是制造大型核反应堆压力容器的主体材料,其特殊工作环境要求其必须具有很高的抗辐照脆化敏感性、淬透性、耐蚀性和断裂韧性[3-4]。在锻造热成形时,RPV(reactor pressure vessel)钢的毛坯件质量一般是成品质量的3倍以上[5],为了获得优良的微观组织和性能,研究Mn-Ni-Mo系低碳合金钢的热塑性变形机理进而确定其合理的热变形工艺参数有着重要的现实意义。目前国内外关于Mn-Ni-Mo系低碳合金的研究主要集中在热处理、焊接性能和合金元素对机械性能的影响方面[6-8]。朱峰等[9]分析了SA508-3低合金钢的动态软化机制与高温锻造热力参数之间的内在关系;权国政等[10]表征了不同变形条件对退火态20MnNiMo钢动态再结晶体积分数的影响;LEE等[11]从显微组织方面研究了影响SA508-3低合金钢断裂韧性的主要因素。而目前结合热加工图描述该合金的高温压缩流变行为及热成形性能的相关研究鲜见报道。为此,本文作者对铸态Mn-Ni-Mo系低碳合金进行高温热压缩试验,以温度为950~1 250 ℃、应变速率0.01~10 s-1时的真应力-应变曲线为研究对象,通过构建变参数的Arrhenius本构模型与人工神经网络模型(artificial neural network model, ANN),同时建立基于动态材料模型理论(DMM)的热加工图,探讨该合金的热变形行为,进而为开展Mn-Ni-Mo系核电用钢塑性成形有限元数值模拟和热加工工艺的选择提供理论支撑和指导。
1 材料和实验方法
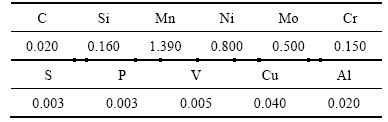
实验试样选用铸态Mn-Ni-Mo系核电用钢,化学成分如表1所示。通过线切割制成直径×长度为8 mm×12 mm的圆柱体,并修磨光滑。在热模拟试验机机上进行高温热压缩实验。设计变形温度分别为950,1 050,1 150和1 250 ℃,应变速率分别为0.01,0.1,1和10 s-1,每组试样的最大应变为0.9。试样在压缩前首先以10 ℃/s的加热速率升温到1 300 ℃,保温5 min,以得到均匀的奥氏体组织;然后,以5 ℃/s的速率降温至变形温度并保温15 s以消除试验试样内部的温度梯度,随后,在设定的温度和应变速率下进行等温压缩,变形结束后立即对试样进行氦气冷却以保留高温变形组织。
表1 试验用合金的主要化学成分(质量分数)
Table 1 Main chemical composition of studied alloy %
2 实验结果与分析
2.1 流变应力曲线
基于热压缩实验数据,建立了如图1所示的真应力-应变曲线。由图1可知:流变应力对变形温度、应变速率和应变较敏感,合金在热压缩过程中发生了明显的动态回复和动态再结晶现象。总体来看,变形过程可分为3个阶段:第1阶段(加工硬化),由于变形程度较小,晶内储存能低,内部组织只发生了少量的动态回复,加工硬化作用远大于软化作用,导致流变应力随着应变的增加而迅速升高;第2阶段(动态软化),随着变形程度增大,动态再结晶(DRX)和动态回复(DRV)带来的软化效应越来越明显,流变应力的升高逐渐减缓至峰值;第3阶段(稳态变形阶段),动态回复、动态再结晶带来的软化作用与加工硬化达到动态平衡,真应力-应变曲线趋于平直。在相同应变下,当温度一定时,随着应变速率增加,真应力增加,这是位错密度的短时间内急剧增加所致;而当应变速率一定时,随着温度升高,真应力下降,这是由于温度的升高导致原子间的相互作用减弱,使得原子的扩散速度加快,位错滑移的阻力变小,但可以看出都不是简单的线性关系。
2.2 变参数Arrhenius流变应力模型构建
金属和合金的热加工变形过程受激活能Q的影响和控制,而影响流变应力变化的主要因素有变形量、变形温度和应变速率,其中变形温度和应变速率对真应力的变化影响最为显著。包含变形热激活能Q和温度T的本构模型[12-13]为
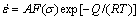 (1)
(1)
在不同的应力水平下,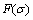 有以下3种表现形式:
有以下3种表现形式:
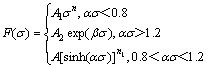
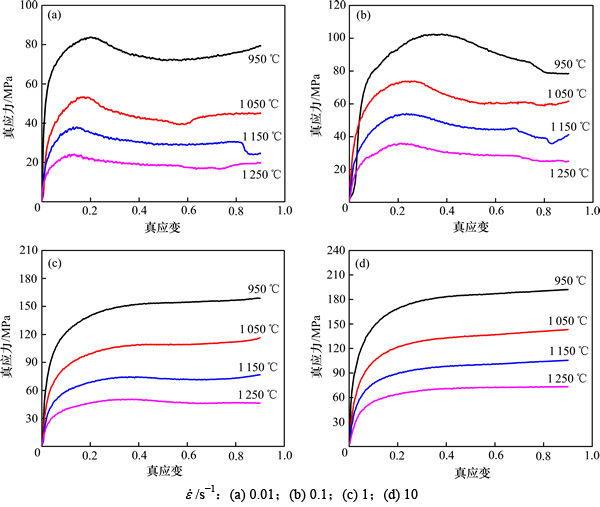
图1 不同变形条件下Mn-Ni-Mo低合金钢真应力-应变曲线
Fig. 1 True stress-stain curves of Mn-Ni-Mo low alloy steel under different deformation conditions
式中: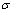 为流变应力,MPa;
为流变应力,MPa;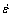 为应变速率,s-1;n和n1为加工硬化指数;A,A1,A2,β和
为应变速率,s-1;n和n1为加工硬化指数;A,A1,A2,β和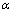 为与温度无关的材料常数,且
为与温度无关的材料常数,且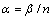 ;
;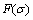 为应力的函数;Q为热变形激活能,kJ/mol;R为摩尔气体常数,8.314 J/(mol·K);T为绝对温度,K。
为应力的函数;Q为热变形激活能,kJ/mol;R为摩尔气体常数,8.314 J/(mol·K);T为绝对温度,K。
金属或合金在热加工变形时,应变速率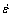 受到热激活控制,为了综合衡量变形温度T和变形速率
受到热激活控制,为了综合衡量变形温度T和变形速率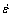 对流变行为的影响,ZENER等[14]提出了温度补偿的变形速率因子Z:
对流变行为的影响,ZENER等[14]提出了温度补偿的变形速率因子Z:
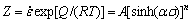 (2)
(2)
将式(2)进行变形便可得到含Arrhenius项的Z参数描述的流变应力表达式:
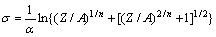 (3)
(3)
基于真应力-应变曲线,式(1)中的材料常数可以通过线性拟合关系分别确定。由于所给定公式中并未涉及应变ε对流变应力的影响,这里以应变ε = 0.3时的实验数据来计算模型中的未知数。对于低应力水平(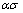 <0.8)和高应力水平(
<0.8)和高应力水平(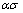 >1.2)时,分别将式(1)取自然对数得到:
>1.2)时,分别将式(1)取自然对数得到:
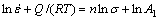 (4)
(4)
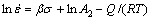 (5)
(5)
由式(4)和(5)可知,当温度一定时,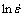 分别与
分别与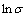 和
和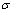 成线性关系,利用偏微分可求得:
成线性关系,利用偏微分可求得:
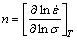 (6)
(6)
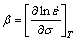 (7)
(7)
基于应变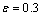 时的实验数据绘制
时的实验数据绘制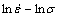 和
和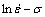 的拟合关系如图2(a)和2(b)所示。
的拟合关系如图2(a)和2(b)所示。
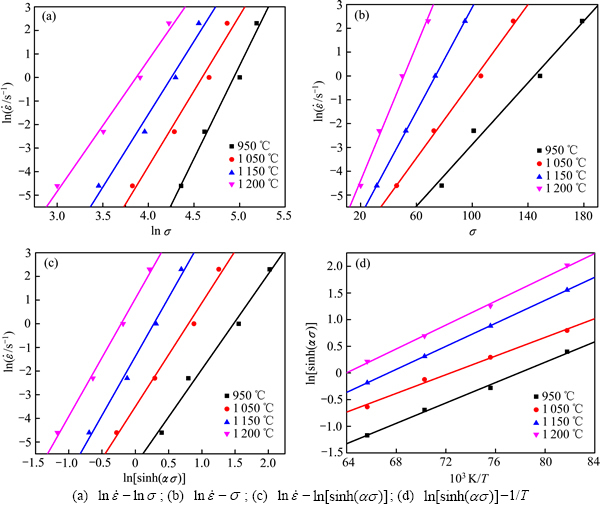
图2 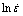 -
-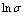 ,
, 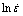 -
-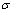 ,
, 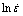 -
-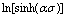 and
and 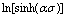 -1/T线性拟合关系
-1/T线性拟合关系
Fig. 2 Relationships between 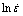 -
-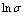 ,
, 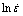 -
-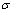 ,
, 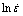 -
-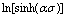 and
and 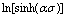 -1/T
-1/T
根据式(6)和(7)可知:其斜率即分别为材料常数n和β。采用最小二乘法进行线性回归求解斜率,得到:n=6.519 2,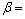 0.099 1。从而可得:
0.099 1。从而可得: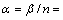 0.015 2 MPa-1。对于所有应力,将式(1)取自然对数得到:
0.015 2 MPa-1。对于所有应力,将式(1)取自然对数得到:
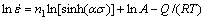 (8)
(8)
 (9)
(9)
当变形温度和应变速率分别一定时,利用偏微分可分别求得:
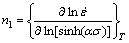 (10)
(10)
 (11)
(11)
根据式(10)和(11)可知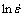 -
-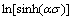 和
和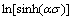 -
-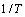 拟合关系曲线斜率即分别为n1和Q,如图2(c)和2(d)所示。可得到:n1=4.593 4,
拟合关系曲线斜率即分别为n1和Q,如图2(c)和2(d)所示。可得到:n1=4.593 4, 384.379 6 kJ/mol。由式(8)可知图2(c)中的截距为
384.379 6 kJ/mol。由式(8)可知图2(c)中的截距为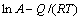 ,分别将对应的截距和Q,R,T,n1代入即可得A=4.6×1013。分别将Q,α,n和A代入式(1)~(3)即可得到Mn-Ni-Mo系核电钢基于应变
,分别将对应的截距和Q,R,T,n1代入即可得A=4.6×1013。分别将Q,α,n和A代入式(1)~(3)即可得到Mn-Ni-Mo系核电钢基于应变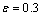 时的热变形流变应力模型:
时的热变形流变应力模型:
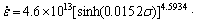
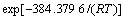 (12)
(12)
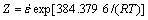 (13)
(13)
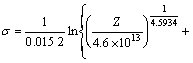
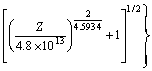 (14)
(14)
考虑应变对合金热变形时流变应力的影响,以对应不同应变下(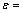 0.05~0.90,按间隔0.05取值)计算求得的材料参数Q,
0.05~0.90,按间隔0.05取值)计算求得的材料参数Q,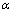 ,n1和
,n1和 来建立合金的Arrhenius本构模型。经过多元线性拟合分析和计算,得出各参数与应变之间存在一定函数关系,并通过7次多项式拟合其函数关系,其相关系数分别达到 0.990 4,0.998 5,0.992 5和0.989 6,如图3所示。各参数随应变变化的7次多项式拟合函数关系式如式(15)所示。由图3可知:在应变较小时,
来建立合金的Arrhenius本构模型。经过多元线性拟合分析和计算,得出各参数与应变之间存在一定函数关系,并通过7次多项式拟合其函数关系,其相关系数分别达到 0.990 4,0.998 5,0.992 5和0.989 6,如图3所示。各参数随应变变化的7次多项式拟合函数关系式如式(15)所示。由图3可知:在应变较小时,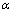 随应变的增加而逐渐减小,然后趋于稳定。Q,n1和
随应变的增加而逐渐减小,然后趋于稳定。Q,n1和 则随应变的增加而逐渐减小。说明Mn-Ni-Mo系核电钢的热变形激活能Q等材料参数都不是常数,而是随应变的改变而发生变化。
则随应变的增加而逐渐减小。说明Mn-Ni-Mo系核电钢的热变形激活能Q等材料参数都不是常数,而是随应变的改变而发生变化。
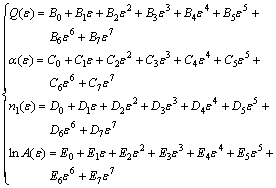 (15)
(15)
由式(3)和(15)可得Mn-Ni-Mo系核电钢引入应变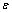 的含Z参数的热变形流变应力模型:
的含Z参数的热变形流变应力模型:
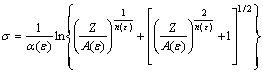 (16)
(16)
2.3 人工神经网络模型
人工神经网络模型(artificial neural network,ANN)擅长分析输入与输出元素之间内在的多元非线性关系问题,因其极高的准确性而得到越来越多的应用[15-16]。本文采用三层前馈误差反向传播网络建立Mn-Ni-Mo系核电钢的本构模型,网络模型结构如图4所示。基于真应力-应变曲线,为了与Arrhenius模型对比,同样取不同应变下作为数据样本。由于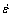 ,T和
,T和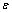 差别很大,在网络训练前需要对样本进行初始化,初始化公式为
差别很大,在网络训练前需要对样本进行初始化,初始化公式为
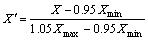 (17)
(17)
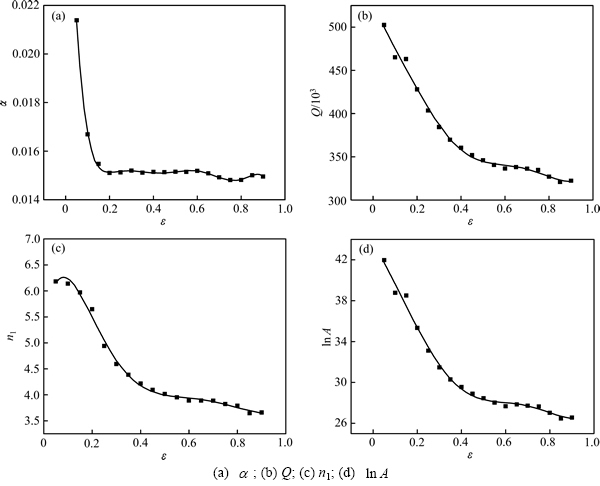
图3 材料参数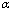 ,Q,n 1,
,Q,n 1,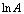 与应变的7次多项式拟合关系
与应变的7次多项式拟合关系
Fig. 3 Relationships of seventh-time polynomial fit between material constants 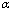 , Q, n1,
, Q, n1, 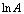 and strain
and strain
式中:X为流变应力试验值;Xmin和Xmax分别为流变应力的最小值和最大值;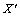 为初始化后的流变应力。
为初始化后的流变应力。
为了保证每个变量都在同一范围内进行训练和测试,每个变量(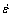 ,
,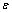 ,T,
,T,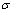 )均进行归一化处理,再对输出变量进行反归一化处理。输入层、隐藏层及输出层神经元数分别为3,10,1,输出流变应力
)均进行归一化处理,再对输出变量进行反归一化处理。输入层、隐藏层及输出层神经元数分别为3,10,1,输出流变应力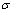 。输入层和隐藏层之间采用对数S型传递函数,隐藏层和输出层则采用线性函数进行传递。将应变为0.3时的样本数据作为有效值不进入模型训练和测试,用来对模型的泛化能力进行验证。数据中的80%作为训练样本,其余20%作为测试样本。网络采用LM梯度下降法,训练目标相对误差为0.001。
。输入层和隐藏层之间采用对数S型传递函数,隐藏层和输出层则采用线性函数进行传递。将应变为0.3时的样本数据作为有效值不进入模型训练和测试,用来对模型的泛化能力进行验证。数据中的80%作为训练样本,其余20%作为测试样本。网络采用LM梯度下降法,训练目标相对误差为0.001。
2.4 流变应力模型预测结果与分析
为了验证引入应变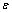 的Arrhenius本构模型和ANN模型的准确度,分别取不同变形工艺条件下2种模型的预测应力值和实验值进行对比,如图5所示。从图5可以看出:2类模型预测值都在最佳回归线附近,但ANN模型的精度更高。为了进一步定量评估模型的准确度,本文利用相关系数(R)及平均相对误差(Eave)对模型进行精确度评价。
的Arrhenius本构模型和ANN模型的准确度,分别取不同变形工艺条件下2种模型的预测应力值和实验值进行对比,如图5所示。从图5可以看出:2类模型预测值都在最佳回归线附近,但ANN模型的精度更高。为了进一步定量评估模型的准确度,本文利用相关系数(R)及平均相对误差(Eave)对模型进行精确度评价。
 (18)
(18)
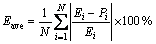 (19)
(19)
其中:Ei为实验值;Pi为模型计算值;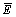 和
和 分别为Ei和Pi的平均值;N为样本数。
分别为Ei和Pi的平均值;N为样本数。
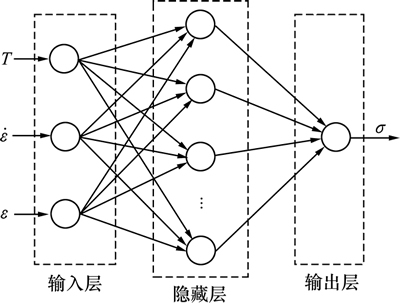
图4 神经网络模型结构
Fig. 4 Schematic illustration of ANN structure
根据图5中的实验值和模型预测值计算R和Eave,结果显示ANN模型的预测结果更准确,其相关系数及平均相对误差分别为0.998和1.31%,Arrhenius模型预测值与实验值相关系数(R)及平均相对误差(Eave)分别为0.991和7.08%。将温度为950~1 250 ℃和应变速率为0.01~10 s-1时的热压缩实验值分别与引入应变 的变参数Arrhenius本构模型和ANN模型的计算值进行对比分析,分别如图6和图7所示。从图6和7可以看出:ANN模型能更精确地反应该合金的流变行为,对锻造等热成型工艺中温度、变形速度、应变参数的制定更具参考价值。
的变参数Arrhenius本构模型和ANN模型的计算值进行对比分析,分别如图6和图7所示。从图6和7可以看出:ANN模型能更精确地反应该合金的流变行为,对锻造等热成型工艺中温度、变形速度、应变参数的制定更具参考价值。
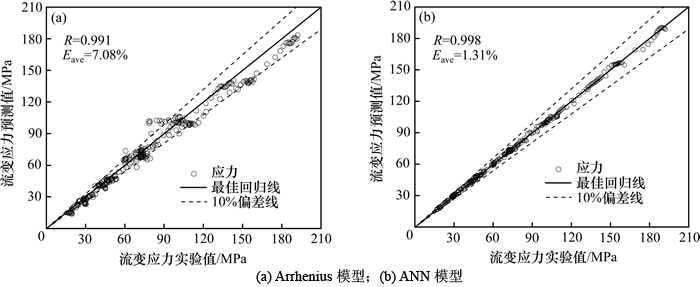
图5 不同变形条件下流变应力与本构模型预测结果相关性
Fig. 5 Correlations between experimental and predicted flow stress at different conditions
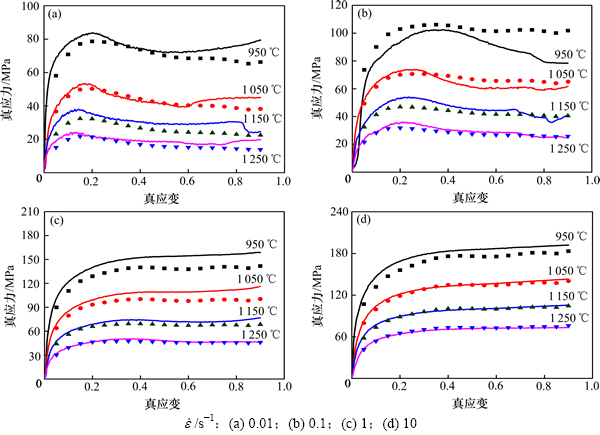
图6 Arrhenius模型预测流变应力与实验值比较
Fig. 6 Comparison between predicted and measured flow stress curves by Arrhenius equation under different strain-rates
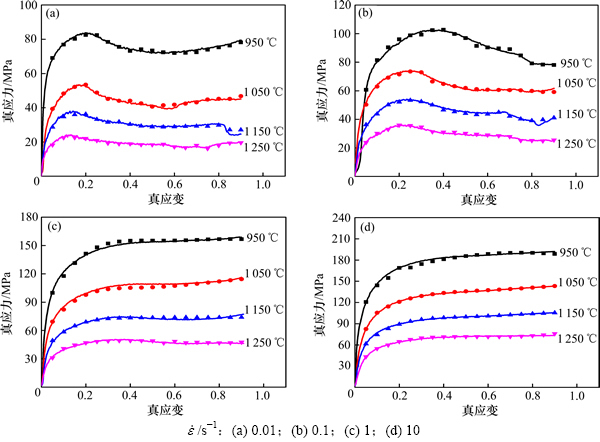
图7 ANN模型预测流变应力与实验值比较
Fig. 7 Comparison between predicted and measured flow stress curves by ANN model under different strain-rates
3 动态材料模型热加工图
根据大塑性变形连续介质力学和不可逆力学理论,PRASAD等[17]提出了基于动态材料模型理论(dynamic materials model,DMM)的热加工图,可较准确地分析材料在不同变形温度和应变速率下微观组织的演化,同时也可获得热变形时的安全区和危险区。现已被广泛应用于材料高温变形机制的分析与热变形工艺的制定,如钛合金、镁铝合金和不锈钢等金属材料[18-20]。根据动态材料模型理论,金属在热变形时吸收的来自工具的功率P由转化为热量的功率耗散量G和组织演化的功率耗散协量J组成[21]:
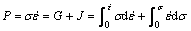 (20)
(20)
热变形过程中,当温度和变形速率一定时,材料的本构关系可表示为
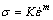 (21)
(21)
式中:K为常数;m为应变速率敏感性指数,
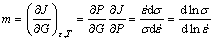 (22)
(22)
功率耗散系数η是与材料内部显微组织演化直接相关的参数,其随变形温度和应变速率的变化关系即构成了功率耗散图,可以由应变速率敏感指数m来表示:
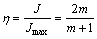 (23)
(23)
由于在加工失稳区(危险区)的功率耗散效率可能也会很高,所以,η大不代表材料的可加工性能好。因此,失稳参数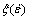 [20]可以用来表示热塑性变形时的连续失稳判据(式(20)),其随变形温度和应变速率的变化关系即构成了流变失稳图。
[20]可以用来表示热塑性变形时的连续失稳判据(式(20)),其随变形温度和应变速率的变化关系即构成了流变失稳图。
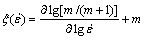 ≤0 (24)
≤0 (24)
根据热压缩实验数据,将不同变形条件下的真应力和应变进行3次样条函数拟合,得到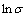 关于
关于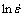 的拟合关系式(25)。代入式(22)可求得特定变形量下的应变速率敏感指数m,进而根据式(23)和式(24)分别求得η和
的拟合关系式(25)。代入式(22)可求得特定变形量下的应变速率敏感指数m,进而根据式(23)和式(24)分别求得η和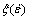 。
。
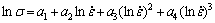 (25)
(25)
式中:a1~a4为与材料有关的常数。
将应变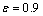 的功率耗散图与流变失稳图叠加可得到材料的热加工图[22],如图8所示,等值线的数字代表功率耗散因子η,图中灰色区域为流变失稳区。由图8可知:Mn-Ni-Mo系核电钢功率耗散较大值主要分布在应变速率适中的范围内(0.1~1 s-1),而流变失稳区主要集中在低温低应变速率和高温高应变速率内。这是因为当温度较低时,原子的扩散能力较弱,晶内储存能较低,位错的运动和晶界的迁移缓慢,动态再结晶(DRX)难以形核和长大;当温度较高时,由于应变速率较大,位错密度在短时间内急剧攀升,合金内形成大量的变形能,在变形过程中产生的热量难以及时散出,容易形成绝热剪切带,出现绝热剪切效应,使得合金产生流变失稳现象。一般认为在热加工的安全区域,功率耗散因子η越大,材料的热加工性能越好,越容易获得均匀细小的动态再结晶组织,因此具有较高功率耗散效率的稳态变形区间可作为最佳的变形工艺参数。根据热加工图可知,当应变
的功率耗散图与流变失稳图叠加可得到材料的热加工图[22],如图8所示,等值线的数字代表功率耗散因子η,图中灰色区域为流变失稳区。由图8可知:Mn-Ni-Mo系核电钢功率耗散较大值主要分布在应变速率适中的范围内(0.1~1 s-1),而流变失稳区主要集中在低温低应变速率和高温高应变速率内。这是因为当温度较低时,原子的扩散能力较弱,晶内储存能较低,位错的运动和晶界的迁移缓慢,动态再结晶(DRX)难以形核和长大;当温度较高时,由于应变速率较大,位错密度在短时间内急剧攀升,合金内形成大量的变形能,在变形过程中产生的热量难以及时散出,容易形成绝热剪切带,出现绝热剪切效应,使得合金产生流变失稳现象。一般认为在热加工的安全区域,功率耗散因子η越大,材料的热加工性能越好,越容易获得均匀细小的动态再结晶组织,因此具有较高功率耗散效率的稳态变形区间可作为最佳的变形工艺参数。根据热加工图可知,当应变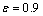 时,Mn-Ni-Mo系核电钢热压缩变形的安全区域可分为2部分:一部分是变形温度为950~1 250 ℃区域,应变速率为0.06~0.30 s-1(Zone Ⅰ),功率耗散系数的浮动范围是0.43≤
时,Mn-Ni-Mo系核电钢热压缩变形的安全区域可分为2部分:一部分是变形温度为950~1 250 ℃区域,应变速率为0.06~0.30 s-1(Zone Ⅰ),功率耗散系数的浮动范围是0.43≤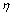 ≤0.54;另一部分是变形温度为1 100~1 250 ℃区域,应变速率为0.3~1.0 s-1(Zone Ⅱ),功率耗散系数的浮动范围是0.39≤
≤0.54;另一部分是变形温度为1 100~1 250 ℃区域,应变速率为0.3~1.0 s-1(Zone Ⅱ),功率耗散系数的浮动范围是0.39≤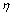 ≤0.44。
≤0.44。
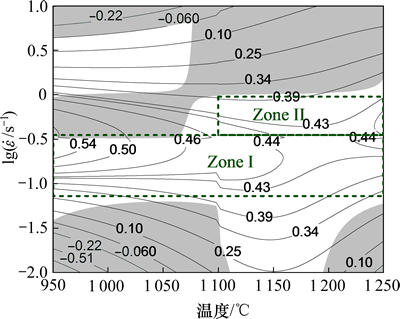
图8 Mn-Ni-Mo合金在应变为0.9时的加工图
Fig. 8 Processing map for Mn-Ni-Mo alloy at strain of 0.9
4 结论
1) Mn-Ni-Mo系核电钢在温度为950~1 250 ℃、应变速率0.01~10 s-1时的真应力-应变曲线具有动态回复和动态再结晶现象。在相同应变下,当温度一定时,合金的流变应力随应变速率的增加而增加;当应变速率一定时,流变应力随变形温度的升高而减小。
2) 基于热压缩实验数据,分别通过多重线性回归和神经网络构建出Mn-Ni-Mo系核电钢高温流变应力模型。对比2种模型的预测值和实验值的相对误差发现,ANN模型对该合金流变行为的预测更准确,其相关系数及平均相对误差分别为0.998和1.31%。
3) 加工图由功率耗散图和失稳图叠加而得,根据加工图可以确定该合金有2个最佳变形区:变形温度为950~1 250 ℃,应变速率0.06~0.3 s-1(Zone I),功率耗散系数0.43≤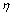 ≤0.54;变形温度为1 100~1 250 ℃,应变速率0.3~1 s-1(Zone II),0.39≤
≤0.54;变形温度为1 100~1 250 ℃,应变速率0.3~1 s-1(Zone II),0.39≤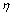 ≤0.44。
≤0.44。
参考文献:
[1] 李承亮, 张明乾. 压水堆核电站反应堆压力容器材料概述[J]. 材料导报, 2008, 22(9): 65-68.
LI Chengliang, ZHANG Mingqian. Overview of reactor pressure vessel steel in PWR nuclear power plant[J]. Materials Review, 2008, 22(9): 65-68.
[2] WEI Guo, DONG Shiyun, WEI Guo, et al. Microstructure and mechanical characteristics of a laser welded joint in SA508 nuclear pressure vessel steel[J]. Materials Science and Engineering A, 2015, 625: 65-80.
[3] WANG Menghan, LI Yufeng, WANG Wenhao, et al. Quantitative analysis of work hardening and dynamic softening behavior of low carbon alloy steel based on the flow stress[J]. Materials and Design, 2013, 45: 384-392.
[4] LEE K H, KIM M C, YANG W J, et al. Evaluation of microstructural parameters controlling cleavage fracture[J]. Materials Science and Engineering A, 2013, 565: 158-164.
[5] 朱峰, 曹起骧, 徐秉业, 等. 核电锻件微观组织性能控制锻造[J]. 塑性工程学报, 1995, 2(1): 8-14.
ZHU Feng, CAO Qixiang, XU Bingye, et al. The control forging for microstructure and property on heavy forgings in nuclear power plant[J]. Journal of Plasticity Engineering, 1995, 2(1): 8-14.
[6] SHENG Zhongqi, HONG Xiao, FENG Peng, et al. Refinement of grain structure in 20MnNiMo steel[J]. China Nuclear Science and Technology Report, 1997, 28(22): 1-8.
[7] 钟志平, 陈英. 20MnMoNi55钢的后动态再结晶模型[J]. 塑性工程学报, 2000, 7(2): 23-26.
ZHONG Zhiping, CHEN Ying. The model of post dynamic recrystallization of 20MnMoNi55 steel[J]. Journal of Plasticity Engineering, 2000, 7(2): 23-26.
[8] ZHANG Xianhui. The characteristics of welding hydrogen crack in 20MnNiMo steel[J]. Transactions of China Welding Institution, 2002, 23: 23-25.
[9] 朱峰, 曹起骧, 徐秉业. 高温锻造中ASME SA508-3钢的动态软化[J]. 清华大学学报(自然科学版), 1999, 39(4): 13-16.
ZHU Feng, CAO Qixiang, XU Bingye. Dynamic softening mechanism on steel of ASME SA508-3 during hot working[J]. Journal of Tsinghua University (Natural Edition), 1999, 39(4): 13-16.
[10] 权国政, 余春堂, 刘莹莹, 等. 20MnNiMo钢热塑性变形与动态再结晶软化的耦合行为[J]. 材料热处理学报, 2013, 34(8): 177-183.
QUAN Guozheng, YU Chuntang, LIU Yingying, et al. Characterization of dynamic rescrystallization behavior of 20MnNiMo steel by thermal deformation[J]. Transaction Materials and Heat Treatment, 2013, 34(8): 177-183.
[11] LEE B S, KIM M C, YOON J H, et al. Characterization of high strength and high toughness Ni-Mo-Cr low alloy steels for nuclear application[J]. International Journal of Pressure Vessels and Piping, 2010, 87(1): 74-80.
[12] LIN Yongcheng, XIA Yuchi, CHEN Xiaomin, et al. Constitutive descriptions for hot compressed 2124-T851 aluminum alloy over a wide range of temperature and strain rate[J]. Computational Materials Science, 2010, 50(1): 227-233.
[13] LIN Yongcheng, CHEN Xiaomin. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working[J]. Materials and Design, 2011, 32(4): 1733-1759.
[14] ZENER C, HOLLOMON H. Effect of strain-rate upon plastic flow of steel[J]. Journal of Applied Physical, 1944, 15(1): 22-27.
[15] LIN Yongcheng, ZHANG Jun, ZHONG Jue. Application of neural networks to predict the elevated temperature flow behavior of a low alloy steel[J]. Computational Materials Science, 2008, 43(4): 752-758.
[16] QUAN Guozheng, YU Chuntang, LIU Yingying, et al. A comparative study on improved arrhenius-type and artificial neural network models to predict high-temperature flow behaviors in 20MnNiMo Alloy[J]. The Scientific World Journal, 2014(1): 1-12.
[17] PRASAD Y V R K, GEGEL H L, DORAIVELU S M, et al. Modeling of dynamic material behavior in hot deformation: forging of Ti-6242[J]. Metallurgical and Materials Transactions A, 1983, 15(10): 1883-1892.
[18] 韦莉莉, 潘清林, 周坚, 等. Al-Zn-Mg-Cu-Zr合金加工图的构建及失稳分析[J]. 中南大学学报(自然科学版), 2013, 44(5): 1798-1804.
WEI Lili, PAN Qinglin, ZHOU Jian, et al. Processing maps and flow instability analysis of Al-Zn-Mg-Cu-Zr alloy[J]. Journal of Central South University (Science and Technology), 2013, 44(5): 1798-1804.
[19] QUAN Guozheng, WANG Yang, YU Chuntang, et al. Hot workability characteristics of as-cast titanium alloy Ti-6Al-2Zr-1Mo-1V: A study using processing map[J]. Materials Science and Engineering A, 2013, 564: 46-56.
[20] WANG Menghan, HUANG Long, CHEN Mingliang, et al. Processing map and hot working mechanisms of Cu-Ag alloy in hot compression process[J]. Journal of Central South University, 2015, 22(3): 821-828.
[21] PRASAD Y V R K. Modeling of hot deformation for microstructural control[J]. International Materials Reviews, 1998, 43(6): 243-258.
[22] PRASAD Y V R K. Processing maps: a status report[J]. Journal of Materials Engineering and Performance, 2003, 12(6): 638-645.
(编辑 赵俊)
收稿日期:2016-03-15;修回日期:2016-06-15
基金项目(Foundation item):中央高校基本科研业务费专项资助项目(CDJZR14130006) (Project(CDJZR14130006) supported by the Fundamental Research Funds for the Central Universities of China)
通信作者:王梦寒,博士(后),副教授,硕士生导师,从事金属塑性成形工艺及模具CAD/CAE/CAM技术研究;E-mail: cquwmh@163.com