­­Numerical simulation of solidification morphologies of Cu-0.6Cr casting alloy using modified cellular automaton model

TSAI De-chang, HWANG Weng-sing

Department of Materials Science and Engineering, National Cheng Kung University, Tainan 70101, Taiwan, China

Received 17 September 2009; accepted 9 April 2010

Abstract: The purpose of this study is to predict the morphologies in the solidification process for Cu-0.6Cr (mass fraction, %) alloy by vacuum continuous casting (VCC) and verify its accuracy by the observed experimental results. In numerical simulation aspect, finite difference (FD) method and modified cellular automaton (MCA) model were used to simulate the macro-temperature field, micro-concentration field, nucleation and grain growth of Cu-0.6Cr alloy using real data from actual casting operations. From the observed casting experiment, the preliminary grain morphologies are the directional columnar grains by the VCC process. The solidification morphologies by MCAFD model are in agreement with the result of actual casting experiment well.

Key words: Cu-Cr alloy; vacuum continuous casting; solidification morphology simulation; modified cellular automaton model; finite difference method

1 Introduction

Vacuum continuous casting (VCC) is used internationally as one of the main methods to generate the high specification metals. Products of this process display high quality, purity and proportionality distribution, which after further processing such as drawing or extruding could be readily supplied as wires and tubes to various high-tech specialty electronics industry.

In the refined metal casting process, grain size distribution and proportionality often cause sizing effects during post-casting treatments, and hence affect the final product quality. The purpose of this study is to develop a computer-based simulation to analyze the solidification heat transfer process during continuous casting of refined copper. Optimization is done by changing key operation parameters to detect and eliminate the presence of defects.

Solidification is an important stage in metallic materials processing. It determines bulk microstructure formation which is directly related to the characteristics of material. The focus of this study is to manipulate different operation conditions such as temperature gradient, growth rate and casting temperatures to control the microstructure formation during solidification and thus to improve the material properties. Earlier studies on this topic were conducted on the basis of physical cast metallography observation and analysis under different operating conditions. Although viable, this method involves excessive manpower, resources and time. Alternative solutions are now sought by utilizing the rapid evolvement in numerical modeling techniques to relate physical parameters and simulate the solidification process. Using numerical simulation not only would allow for more economical and efficient operations, but also predictions on microstructure changes with respect to change in operation conditions can be easily made. This would help to reduce the formation of defects in a cast and thus improve quality of the finished product.

Initiations of numerically simulated microstructure formation began in 1966. OLDFIELD[1] introduced the concepts including nucleation and growth rate as a function of heat transfer on the basis of simulating temperature distribution in the solidification process. This was done to obtain an approximation in the microstructure formation process during solidification. However, due to computational and macroscopic modelling limitations, developments in this area progressed extremely slowly. In 1966-1984, only one publication in this area was published by STEFANESCU and TRUFINESCU[2]. In the mid 1980s, computer industry progressed rapidly along with a gradually optimized and refined numerical characterisation and theories in solidification. This stimulated the maturity of macroscopic simulation, especially in terms of heat transfer. Consequently, an increase in overall interest on this topic has been raised internationally by scholars and reports on related works are now published in large volumes.

The simulation of continuous casting process is mainly focused on fluid flow, heat transfer and solidification phenomenon. In 1997, HIROKAZU and ITSUO[3] compared the temperature distribution profile of copper under various casting speeds. In 1999, HARKKI and MIETTINEN[4] used a commercial program package (FIDAP) to simulate the heat transfer and solidification for copper and brass by upper continuous casting process. The microstructure simulation by continuous casting process was rarely discussed in this period. Until 2005, DING and XU[5] developed a three-dimensional microstructure simulation system of copper by heated mould continuous casting process. The calculation of solute concentration is not considered in this system, so it is only applied to the microstructure simulation of pure metal.

2 Experimental

The experimental equipment used for the VCC of copper chromium alloy bars is shown in Fig.1. The vacuum chamber is equipped with a high frequency induction furnace for melting metals and resistance heating furnace for sustaining the liquid metal temperature. Normal experimental procedures include melting the alloy in vacuum, gas stripping the melt and casting under an inert gas environment.

Fig.1 Illustration of vertical VCC equipment

Pure Cu and the parent Cu-Cr alloy were melted into Cu-0.6Cr (mass fraction, %) in a carbon crucible (IG15) and then were cast into a cylindrical rod with 8 mm in diameter using a carbon mold (IG11) under a nitrogen atmosphere. The outer dimensions for the mold are 20 mm in diameter and 100 mm in height; and for the crucible are 200 mm in diameter and 250 mm in height, as shown in Fig.2.

Fig.2 Photo of graphite mold and crucible in VCC process (Unit: mm)

Continuous casting using the crucible and mold repeatedly failed and pieces of the alloy residue in the crucible were examined. A distinct layer of graphite was found to adhere to the alloy at the bottom of the crucible. Then, the failed bar cast was cut into several smaller pieces using a low-speed saw and prepared for metallurgical examination. The pieces were observed under an optical microscope (OM), and its phases were identified using X-ray diffraction.

To improve this failure problem, a silicon carbide material coated with boron nitrite and zirconia composite was developed in replacement to graphite mold. The outer diameter and height of the new mold are 20 mm and 100 mm, respectively, as shown in Fig.3.

Fig.3 Sketch of silicon carbide mold (Unit: mm)

3 Mathematical model

Two major methods can be used to model cast microstructure: deterministic and probabilistic. In 1966, OLDFIELD[1] associated the heat transfer phenomena and grain growth to simulate crystallization of grey iron in which nucleation changes constantly in proportion to the squared of undercooling. From 1966 to 1984, only STEFANESCU and TRUFINESCU[2] announced a related report in 1974 because of the restrictions of simulation technique. In 1984, HUNT[6] published the instantaneous nucleation model continually on applying the deterministic methods. In terms of categorizing the crystals formed, DUSTIN and KURZ[7] assumed growth of spherical, columnar and cylindrical equiaxed grains.

The deterministic model includes standard transport and phase field technologies. In this model, the distribution of grain texture is decided in the initial stage, and then by utilizing the continuity theory, nucleation, grain growth and grain selection during the solidification process can be resolved. The characteristic feature of deterministic model is able to resolve average radius of grains and local mean solidification time, but is unable to describe the morphology of individual grains. In thin castings, equiaxed and columnar grains will compete with each other during grain growth. While the grain-orientation has an important role in a cast, the deterministic model neglects the effect of heat flow direction on grain-orientation, and therefore disables accurate evaluation of grain morphology in thin cast products. Moreover, since the grain category is decided in advance, the deterministic model is also unable to deal with the transformation of grain morphology (columnar- equiaxed transformation or equiaxed-columnar transformation). Resultantly, the deterministic model has some drawbacks and restrictions in its applications. These limits can be overcome by the Monte Carlo method developed by BROWN and SPITTLE[8]. Known as the probabilistic model, the Monte Carlo method adopted the rule of the lowest surface energy of grains and combined it with random sample selection to address nucleation, grain growth and solid-liquid phase transformation in metals. The resulting simulation is reasonably similar with a real cast product; however, it showed the lack of physical meanings for many process and material parameters.

Recently, the emphasis has been put on integrating the advantages of both models to form a unified model. RAPPAZ et al[9-11] developed a Cellular Automation method based on the heterogeneous nucleation and adopted a continuous nucleation model. The continuous model is composed of the relationship of Gaussian distribution curve between nucleation densities and undercooling. The nucleation location and direction are then randomly assigned. In the CA model, for growth rate of dendrite tip the deterministic model is adopted based on the physical theories, and for the nucleation distributions, nucleation directions and dendrite growth orientations the probabilistic model is utilized. Therefore, CA method not only possessed the advantages of Monte Carlo method but also had the physical meanings on crystallographic effects and grain selection.

Following previous literature reviews, the heterogeneous nucleation of CA model adopted the Gaussian distribution theory developed by RAPPAZ and GANDIN[12], which explained the relationship between nucleation density and undercooling. Two different Gaussian distribution curves were considered for describing the heterogeneous nucleation on the surface of the casting and in the bulk liquid. The nucleation density of grain n(?T), formed at a certain undercooling temperature, is given by

           (1)

where 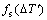 is the solid fraction,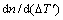is found according to the Gaussian distribution. The algorithm for grain growth with different preferred orientations proposed by RAPPAZ and GANDIN[12] was embedded into the CA growth algorithm. Within the time-step, δt, used for integrating the growth kinetics of the dendrite tips, the size increment of the diagonals of the square associated with a cell “v”, L_v(t), is given by

                           (2)

where v(ΔT) is the growth rate of a dendrite tip at a certain undercooling, which can be calculated by the Kurz-Glicksman-Trivedi (KGT) model[13]. With respect to calculating the temperature distribution during solidification, we adopted Fourier’s fundamental laws of heat transfer in Cartesian coordinates. The resulting relationship used is as follows:

     (3)

where ρ is the density; λ is the thermal conductivity; v_c is the casting speed; q is the latent heat obtained from the temperature recovery method[14]. Calculation of solute concentration used the following formulas:

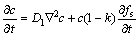                      (4)

                                 (5)

                                    (6)

where D_l is the solute diffusion coefficient in the liquid phase, D_s is the solute diffusion coefficient in the solid phase, k is the partition coefficient and the * is a symbol of S/L interface location. The detailed interpretations could be referred to Ref.[15].

Physical model used to develop the numerical simulation in this study is depicted in Fig.4, where melted metal liquid is shown at the centre. A pure copper withdraw rod is used to extrude Cu-0.6Cr alloy continuously through the silicon carbide mould in vacuum, with cooling water surrounding the mold. The simulated and the experimentally observed micro- structures were then compared to examine reliability of the simulation technique.

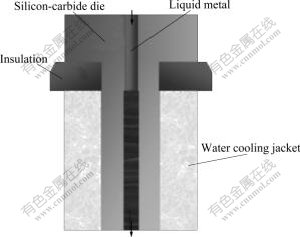
Fig.4 Sketch of physical model in vacuum continuous casting process

4 Results and discussion

Examination of the VCC process will be done in two sections. One focuses on the actual process of VCC to observe and discuss change in the evolution mechanism of solidification microstructure. The other employs finite difference methods to calculate the macroscopic temperature fields and microscopic concentration fields. Then, the MCA methods are used to compute microscopic nucleation and growth mechanism. The models are combined to integrate a macro and microscopic linkage to complete the Cu-0.6Cr alloy VCC solidification microstructure simulation.

4.1 Cu-0.6Cr alloy by VCC process

In the VCC process, the related experimental parameters are listed in Table 1. Prior to experiment, the carbon crucible was preheated to 1 250 ℃ and vacuum was created inside the furnace at a pressure of 10.13 Pa. In the protected atmosphere by argon, the flow rate of cooling water (20 L/min) was fixed to proceed the Cu-0.6Cr VCC process. Fig.5 shows the metallograph of Cu-0.6Cr alloy by VCC process. It can be obviously found that the grain growth character is the columnar grain along the axis from the cross section or longitudinal section. Fig.6 shows the microstructures of Cu-0.6Cr alloy by VCC process under the optical micro- scope, and the observed places of Figs.6(a), (b), (c) and (d) are corresponding to the symbol a, b, c and d in Fig.5. It is clear that the grain shape is stable in the central part of cross or longitudinal section but it is unstable dendrite in the edge of cross or longitudinal section. This grain morphology of Cu-0.6Cr alloy has better mechanical and physical properties.

Table 1 Experimental parameters of vacuum continuous casting

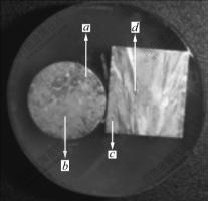
Fig.5 Cross and longitudinal section metallographs of Cu-0.6Cr alloy by VCC process

4.2 Verification of Cu-0.6Cr alloy microstructure simulation

Thermodynamics properties for the Cu-0.6Cr alloy and silicon carbide mould are listed in Table 2. For macroscopic purpose of this study, finite difference methods are used to solve the Fourier heat transfer equations. The resulting temperature distribution is shown in Fig.7. It can be seen from Fig.7 that, the heat transfer mechanism is along axial direction and parallel to the casting direction. This macroscopic temperature field is used as the basis for the development of microscopic nucleation and growth models. Using the solute concentration formulas (4)-(6), the concentration distribution of Cu-0.6Cr alloy can be obtained. The added quantity of chromium is 0.6% (mass fraction). Due to the solute redistribution effect in solidification, the concentration is accumulated to be 1.17% (mass fraction) at S/L interface observed from Fig.8. Fig.9 shows the local area concentration distribution in the region A from Fig.8. The microstructure profiles are also obviously observed in Fig.9. This will affect the behavior of solidification hereafter. As displayed in Fig.10, the integrated model first obtained microscopic nucleation coefficients by inserting the macroscopic temperature field values then determined temperature values required for growth. This is followed by feeding back the relative latent heat released during solidification to the macroscopic temperature evaluation. The process loops until the whole cast object is solidified. Resulting values for cell size and quantity for microscopic nucleation and growth are displayed in Table 3.

Fig.6 Microstructures of Cu-0.6Cr alloy by VCC process: (a) Cross section (edge); (b) Cross section (central); (c) Longitudinal section (edge); (d) Longitudinal section (central)

Table 2 Thermal input parameters in numerical simulation of vacuum continuous casting

Fig.7 Temperature profile of Cu-0.6Cr alloy by VCC process

Fig.8 Solute concentration distribution of Cu-0.6Cr alloy by VCC process

Fig.9 Local area concentration distribution of Cu-0.6Cr alloy by VCC process

Fig.11 shows the microstructure obtained from casting with 250 mm/min extruding speed and 20 L/min cooling water flow rate. With respect to most alloy metals, solidification grain growth direction is usually directly related to temperature gradients and solute concentration. The grain growth follows an axial direction, similar to that predicted from the temperature gradient direction. Further, compared with the experimental casting (cross or longitudinal section), it could be found that the simulated results are similar to the actual casting. Finally, the ASTM standard is used to calculate the average grain size of Cu-0.6Cr alloy, then the accuracy of microstructure predict system is verified in Table 4. 15% of error of average grain size could be attributed to the use of the thermal parameter as constant.

Table 3 Input parameters used in microstructure modelling process of Cu-0.6Cr alloy

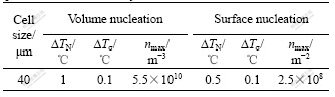
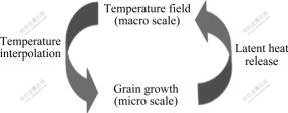
Fig.10 Couple mechanism of macro and micro scale

Fig.11 Cross sectional microstructures of copper rod at casting speed 250 mm/min: (a) Longitudinal; (b) Transverse

Table 4 Average grain size of Cu-0.6Cr alloy by VCC process

1) From the macro temperature calculation, it could be found that the temperature gradient is along the axis direction and the solute redistribution condition from the concentration calculation.

2) The finite difference method is used to obtain the macro temperature field and the micro concentration field, then the MCA mold is coupled to calculate the nucleation and grain growth could effectively predict the microstructure morphology of Cu-0.6Cr alloy by VCC process.

References

[1] OLDFIELD W. A quantitative approach to casting solidification, freezing of cast iron [J]. ASM Trans, 1966, 59: 945-960.

[2] STEFANESCU D M, TRUFINESCU S Z. Crystallization kinetics of grey cast iron [J]. Metallkunde, 1974, 65: 610-615.

[3] HIROKAZU Y, ITSUO O. Computer simulation of solidification in copper billet continuous casting under an assumption of flow field [J]. Japan Inst Metals, 1997, 61: 342-349.

[4] HARKKI K, MIETTINEN J. Mathematical modelling of copper and brass upcasting [J]. Metall Trans B, 1999, 30: 75-98.

[5] DING Yu-tian, XU Guang-ji. Numerical simulation of solidification of continuously cast pure Al [J]. Foundry Technology, 2005, 26: 1075-1078.

[6] HUNT J D. Steady state columnar and equiaxed growth of dendrites and eutectic [J]. Materials Science and Engineering, 1984, 65: 75-83.

[7] DUSTIN I, KURZ W. Modeling of cooling curves and microstructures during equiaxed dendritic solidification [J]. Zeitschrift fuer Metallkunde, 1986, 77: 265-273.

[8] BROWN S G, SPITTLE J A. Computer simulation of the effects of alloy variables on the grain structures of castings [J]. Acta Metallurgical et Materialia, 1989, 37: 1803-1810.

[9] GANDIN C A, RAPPAZ M. Probabilistic modeling of microstructure formation in solidification processes [J]. Acta Metall Mater, 1993, 41: 345-360.

[10] GANDIN C A, RAPPAZ M. A coupled finite element-cellular automaton model for the prediction of dendritic grain structures in solidification processes [J]. Acta Metall Mater, 1994, 42: 2233-2246.

[11] GANDIN C A, RAPPAZ M, THEVOZ P. A three-dimensional cellular automaton-finite element model for the prediction of solidification grain structures [J]. Metall Mater Trans A, 1999, 30: 3153-3165.

[12] RAPPAZ M, GANDIN C A. Prediction of grain structures in various solidification processes [J]. Metall Trans A, 1996, 27: 695-705.

[13] LIPTON J, GLICKSMAN M E, KURZ W. Equiaxed dendrite growth in alloys at small supercooling [J]. Metall Trans A, 1987, 18: 341-345.

[14] XU Zhen-ming, GENG Guan-xiang, LI Jian-guo. Numerical analysis for position and shape of solid-liquid interface during continuous casting of single crystal Cu [J]. Journal of Shanghai Jiaotong University, 2001, 35: 406-410. (in Chinese)

[15] ZHU M F, HONG C P. A three dimensional modified cellular automaton model for the prediction of solidification microstructures [J]. ISIJ International, 2002, 42: 520-526.

 Corresponding author: HWANG Weng-sing; Tel: +886-6-234-4393; E-mail: wshwang@mail.ncku.edu.tw

DOI: 10.1016/S1003-6326(09)60260-0

(Edited by LI Xiang-qun)