Trans. Nonferrous Met. Soc. China 30(2020) 2927-2940

Constitutive modeling of flow behavior of precipitation-hardened AA7022-T6 aluminum alloy at elevated temperature

H. R. REZAEI ASHTIANI, P. SHAHSAVARI

School of Mechanical Engineering, Arak University of Technology, Arak, Iran

Received 22 February 2020; accepted 4 September 2020

Abstract: The thermomechanical behavior of precipitation-hardened aluminum alloy AA7022-T6 was studied using isothermal compression at temperatures of 623-773 K and strain rates of 0.01-1 s^-1. The experimental results indicated that dynamic recrystallization (DRX) is a predominant hot deformation mechanism, especially at elevated temperatures and low strain rates. The modified Johnson-Cook (J-C) and the strain compensated Arrhenius-type models were developed to predict the hot flow behavior under different deformation conditions. The correlation coefficients of modified J-C model and the strain compensated Arrhenius-type models were 0.9914 and 0.9972, respectively, their average relative errors (ARE) were 6.074% and 4.465%, respectively, and their root mean square errors (RMSE) were 10.611 and 1.665 MPa, respectively, indicating that the strain compensated Arrhenius-type model can predict the hot flow stress of AA7022-T6 aluminum alloy with an appropriate accuracy.

Key words: flow behavior; constitutive models; Arrhenius model; dynamic recrystallization; AA7022-T6 aluminum alloy

1 Introduction

The precipitation-hardenable 7xxx series aluminum alloys (Al-Zn-Mg-Cu) have unique mechanical properties and great fatigue resistance, which are thus widely used in the aerospace and transportation industries [1-3]. These parts are usually formed, especially forming processes at elevated temperatures such as hot extrusion, rolling, and forging. The high deformation temperatures, large strains and extensive strain rates of forming processes cause drastic changes in the microstructure of materials [4,5]. Furthermore, the mechanical behaviors of materials are dependent strongly on the microstructural evolution [6,7]. Al-Zn-Mg-Cu alloys have a high value of stacking fault energy and metallurgical phenomena can occur during hot working [8,9]. Thus, in order to have excellent mechanical properties of components, the microstructure should be controlled during the hot deformation processes. The investigation of the hot deformation behavior of 7xxx series alloys is necessary for the selection of optimum processing parameters during thermomechanical processes.

The hardening and softening mechanisms consist of work hardening (WH), dynamic recovery (DRV) and dynamic recrystallization (DRX) as the metallurgical phenomena during hot deformation cause to complicate the mechanical behavior of materials [10-12]. Thus, the complicated microstructure of materials after hot forming significantly affects the strength of metallic products [13-15]. So the prediction of hot deformation behavior of materials is complicated and can only be computed with the assistant of computer code which models the response of the deformed material under the specific loading conditions. For this reason, constitutive equations are mostly used to display material flow behaviors in a form that can be employed in computer code to simulate and model the forming processes and material behavior under the general loading conditions [16-19]. A comprehensive and accurate model for describing the relationship between processing parameters and flow stress is essential to credibly simulate.

The mechanical and microstructural behaviors of metallic and base metal composite materials are investigated by various developed constitutive models which include the phenomenological models [20,21], physically-based models [22,23] and artificial neural networks models [24,25]. These the models can reflect the different deformation mechanisms such as hardening and softening mechanisms on hot flow stress. The most widely used models of these are phenomenological models that the material constants of these models have great importance to the prediction of flow stress at different deforming conditions [4]. The Arrhenius- type and Johnson-Cook (J-C) models are two conventional phenomenological constitutive  models [26-29]. The J-C model can forecast the deformation behaviors of ferrous and nonferrous materials at elevated temperatures [30-32]. The low accuracy of J-C model predictions has led to providing the modified J-C models to more accurately predict the softening and hardening effects of flow behavior [33-35]. The effects of deformation temperature, strain rate and strain are considered in the Arrhenius-type model to   predict the flow stress of materials. The strain compensated Arrhenius model has been developed to accurately predict and exhibit the dynamic softening and work hardening mechanisms during hot deformation [35-38].

In recent years, the thermomechanical and microstructural behavior of aluminum alloys has been investigated because of the significance of hot forming processes of these materials. Accordingly, the noticeable researches have been performed on the various constitutive models to describe and analyze hot flow behavior along with the efficacy of metallurgical phenomena on the trend of material deformation. REZAEI ASHTIANI et al [39] studied hot deformation behavior of pure aluminum alloys and developed strain compensated Arrhenius model as well as reported the WH mechanism due to an increase of dislocation density. LI et al [40] reported the DRV and DRX as softening mechanisms for the deformation behavior of Al-Cu-Li-Sc-Zr at elevated temperature and developed the Arrhenius model. The hot tensile behavior of 2099 Al-Li alloy and Arrhenius equations were investigated by CHEN et al [41]. MOSTAFAEI and KAZEMINEZHAD [42] reported that the DRV occurred during hot compression of Al-6Mg and provided the Arrhenius model. NAYAK and DATE [43] compared the Arrhenius, strain-compensated Arrhenius, J-C and modified J-C models of Al-SiC composite in a board range of strain rate and temperatures. DAI et al [44] analyzed the characteristic hot deformation of 5083 aluminum alloy and DRX occurred at high deformation temperatures and strain rates as well as introduced the strain-compensated Arrhenius equation. LIU  et al [45] characterized the flow behavior of Al-Mg-Si-Mn-Cr alloy at elevated temperature and predicted the phenomenological and physical- based models. SHI et al [46] developed the Arrhenius model and DRV is a dominating mechanism of the hot deformation of homogenized AA7150 aluminum alloys. ZHOU et al [47] indicated the application of the Arrhenius model to simulate the hot compression process to optimize the deformation process of the aluminum base composite. DONG et al [48] simulated the extrusion process of complex profiles of Al-Mg-Si using strain compensated Arrhenius model. Also, ZHANG et al [49] used the material constant of strain compensated Arrhenius model as computer code to simulation extrusion of Al-Zn-Mg. More studies reported that the DRX and DRV were hot deformation mechanisms of aluminum alloys at hot working conditions. Also, the developed models have indicated the complex flow behavior due to dynamic softening mechanisms and accurately described the flow stress of aluminum and composite alloys at hot deformation conditions.

In this study, the mechanical behavior of precipitation-hardened aluminum alloy AA7022-T6 has been investigated at different strain rates and temperatures. The hot deformed microstructures were observed to validate the deformation mechanisms and influence of temperature and strain rate on the microstructural changing of this alloy. The constitutive models were developed based on the modified J-C model and strain compensated Arrhenius-type model, respectively.

2 Experimental

The extruded AA7022 was employed for the hot compression test in this work, whose chemical composition is listed in Table 1. A series of cylindrical samples were machined from the extruded bars in the sizes of 4 and 12 mm in radius and height, respectively. For the preparation of AA7022-T6, the extruded bars were heat-treated at 733K for 1 h in a furnace as solution treatment then followed by water quenching. Then artificial aging heat treatment was employed at 393 K for 16 h to achieve proper precipitation-hardened AA7022-T6 aluminum alloy samples. The optical micrograph of the initial microstructure of the heat-treated alloy is shown in Fig. 1, which indicates that the grains are fibrous along the extrusion direction.

Table 1 Chemical composition of experimental AA7022 alloy (wt.%)

Fig. 1 Initial microstructure of AA7022-T6 alloy

For determination of the flow stress behavior of the AA7022-T6 alloy at elevated temperatures, the hot compression tests were performed using a Gotech-AI7000 universal testing machine at the temperatures of 623, 673, 723 and 773 K with the strain rates of 0.01, 0.1 and 1 s^-1. The AA7022-T6 alloy samples were firstly heated to the forming temperature by the electrical resistance furnace, as each one of them was warmed to test temperature and held for 6 min for the thermal balance. The artificial aging heat treatment and hot compression deformation tests of AA7022-T6 were performed according to the test schedule illustrated in Fig. 2. In order to reduce the interfacial friction effect, a very thin silicate sheet called mica was used between dies and samples as lubricate. The samples were compressed to a strain of 0.6, and then directly quenched in water for preventing the unsought microstructural transformation and maintenance of hot-formed microstructure.

Fig. 2 Artificial aging heat treatment and thermo- mechanical schedule used to compress samples

3 Results and discussion

3.1 True stress-true strain curves

After hot compression tests, the barreled samples are created by changing the stress state from 1D to 3D due to the interfacial friction, although the lubricant was applied for reducing friction between sample and die. Therefore, with the increase of the deformation, the effects of friction increase. Thus, there are heterogeneous deformations as a drum shape of samples and error in measured flow stress. So, the effect of friction should consider experimental data for predicting the accurate flow stress. The corrected flow stress is expressed by [42,50]

         (1)

where σ_c, σ_m and ε_m are the corrected and measured flow stresses and measured strain, respectively; r₀ and h₀ are the initial radius and the initial height of the sample, respectively; and m is the friction factor selected as 0.2 [50]. The comparison of friction corrected and measured flow behavior of AA7022-T6 is illustrated in Fig. 3 at various deformation temperatures and strain rates. The corrected flow stresses are lower than the measured ones, therefore, the effects of friction appear with increasing strain because of increasing contact area between the sample and die. Also, the work hardening effects at original curves are reduced by correction [42]. Figure 3 presents that the influences of the strain rate and temperature on the flow stress are really considerable. The decrease in temperature and the increase of strain rate can increase the flow stress. In addition, the strain effects on the flow stress are significant. Therefore, at the beginning of deformation that the flow stress has low value, stress increases sharply with the increase of strain due to the significant work hardening effect.

3.2 Microstructural evolution

The micrographs observed by the optical microscope of the AA7022-T6 deformed at different strain rates and temperatures are displayed in Fig. 4 and Fig. 5. At the strain rate of 0.01 s^-1, the effects of deformation temperature on the microstructures of deformed samples are shown in Figs. 4(a)-(d). It is observed from Fig. 4 that the microstructure of AA7022 is sensitive to the temperature. At the temperature of 623 K, the microstructure mainly consists of the deformed grains and a little percentage of recrystallized grains is shown in Fig. 4(a). When the deformation temperature increases to 673 K, new recrystallized grains are formed (Fig. 4(b)). At high temperatures of 723 and 773 K (Figs. 4(c) and (d)), many recrystallized and fine grains are observed along the deformed grain boundaries and grain interior. And, the volume fraction of recrystallized grains increases with increasing forming temperature. Thus, at the constant strain rate, the flow stress decreases as the forming temperature increases (see Fig. 4) due to the dynamic recrystallization as a softening mechanism.

Fig. 3 Comparison of original and friction corrected true stress-strain curves of AA7022-T6 alloy with strain rates of 0.01 s^-1 (a), 0.1 s^-1 (b) and 1 s^-1 (c) at various temperatures

Fig. 4 Microstructures of AA7022 alloy deformed at temperatures of 623 K (a), 673 K (b), 723 K (c) and 773 K (d) with strain rate of 0.01 s^-1

Fig. 5 Microstructures of AA7022 alloy deformed at temperatures of 623 K (a) and 723 K (b) with strain rate of 0.1 s^-1

Figures 5(a) and (b) exhibit the micro- structures of the deformed sample at temperatures of 623 and 723 K with a strain rate of 0.1 s^-1. The microstructural observations show that the deformed sample at the temperature of 623 K consists of insignificant recrystallization in the non-uniform grains, while the more recrystallized grains are observed in some deformed areas at the deformation temperature of 723 K.

4 Constitutive equation of flow stress during hot deformation

4.1 Modified J-C model

The modified J-C model, which regards the coupled effects of strain, strain rate and temperature on the mechanical behavior of materials at elevated temperature, was developed by LIN et al [51]. Also, the work hardening, dynamic recovery and dynamic recrystallization are evaluated by this model. The modified J-C model can be represented as

              (2)

where σ is the flow stress for a specified strain, T is the thermodynamic temperature, is the dimensionless strain rate, and can be expressed as , where  and  are strain rate and reference strain rate, respectively; T_r is the reference temperature; B₀, B₁, B₂, C₀, λ₁ and λ₂ are material constants. In this study, the deformation temperature of 623 K and the strain rate of 1 s^-1 were applied as the reference conditions.

Under the reference conditions, Eq. (2) can be written as a function of strain.

σ=B₀+B₁ε+B₂ε²                                 (3)

Replacing the strain values and corresponding flow stress values into Eq. (3) gives the relationship between σ and ε using the second order polynomial fitting, as shown in Fig. 6(a). When the deformation temperature is reference temperature (623 K), Eq. (2) comes as the following:

               (4)

Then, the mean value of C₀ can be taken by the method of linear fitting with different strain rates at the reference temperature from the slopes of the lines in the σ/(B₀+B₁ε+B₂ε²)- plot, as shown in Fig. 6(b).

The final step is to calculate the material constants λ₁ and λ₂. These material constants were replaced by a new parameter λ, here, λ=λ₁+λ₂. λ can be taken by catching the natural logarithm of both sides of Eq. (2).

    (5)

The value of λ can be specified by linear  fitting of the relation between ln{σ/[(B₀+B₁ε+B₂ε²)(1+C₀lnε^·*)]} and T-T_r under different strain rates and temperatures from Fig. 6(c). Therefore, the values of λ₁ and λ₂ were derived by the slopes of the lines in the λ- plot, as shown in Fig. 6(d).

Consequently, all of the material constant values of the constitutive equation of AA7022-T6 alloy based on the modified J-C model are confirmed as shown in Table 2.

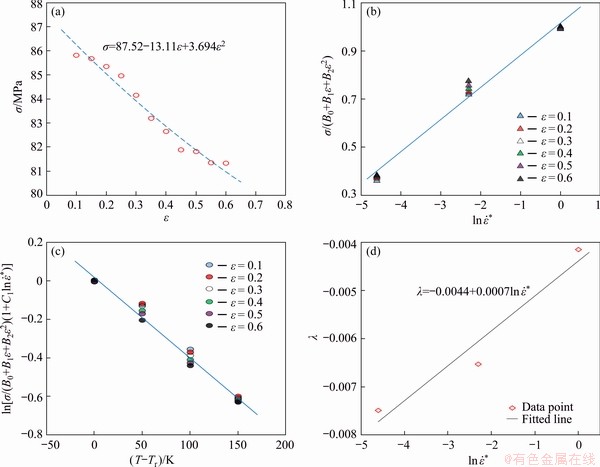
Fig. 6 Relationship between σ and ε at 623 K and 1 s^-1 (a), between σ/(B₀+B₁ε+B₂ε²) and  (b), between ln[σ/(B₀+B₁ε+B₂ε²)(1+ C₀)] and T-T_r (c), between λ and  (d)

Table 2 Material constants based on modified J-C model

The comparison between the predicted values by the modified J-C model and experimental results at different conditions for AA7022-T6 alloy is shown in Fig. 7. As it is clear from this figure, the modified J-C model could correctly predict the flow stress of the AA7022-T6 alloy at elevated temperatures. So, there is a suitable relation between the predicted data and experimental results. It can be seen that some of the predicted data at the temperature of 773 K fitted well with the experimental results. However, the modified J-C model cannot predict the drastic changes due to hardening power as observed at the temperatures 623 and 673 K and the strain rates 0.01 and 0.1 s^-1. Anyway, the modified J-C model can describe the effects of softening and hardening processes on the hot deformation behavior of materials.

4.2 Arrhenius-type model

The Arrhenius-type model has high accuracy for the prediction of the flow behavior of materials in the hot working, SELLARS and McTEGART [52] developed this phenomenological constitutive model. The correlation among the flow stress, strain rate and temperature could be expressed by the power-law at low-stress level, by the exponential law at high-stress level, and by the hyperbolic sine-type equation at all stress levels, which are given by Eqs. (6)-(8).

                       (6)

                  (7)

               (8)

where Q is the deformation activation energy, R is the universal gas constant, and A, n′, n, β and α (α=β/n′) are material constants.

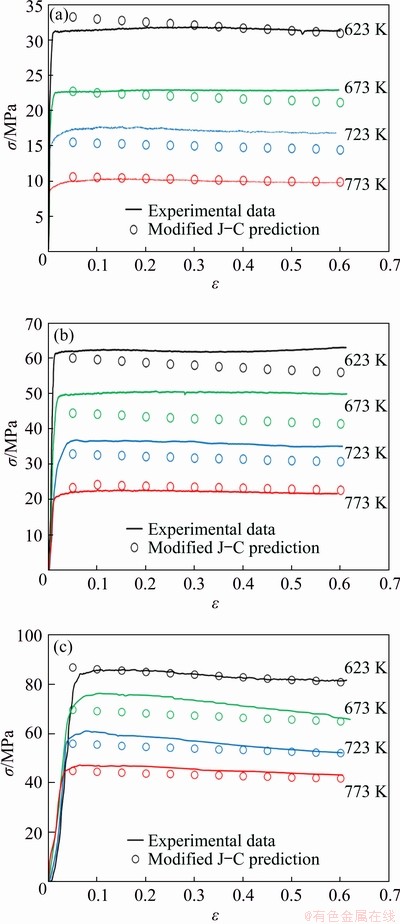
Fig. 7 Comparison between experimental and predicted flow stress by modified J-C model of AA7022 alloy at strain rates of 0.01 s^-1 (a), 0.1 s^-1 (b) and 1 s^-1 (c)

Generally, the high and low levels of stress are described by the power-law and the exponential law, respectively. However, the hyperbolic law in the Arrhenius-type equation gives better estimations between flow stress and Z in the whole ranges of hot working (Eq. (6)) [53]. However, the interpretation of flow stress is imperfect by these equations, because it is not considered the strain effects on the flow stress of AA7022-T6 at elevated temperature.

4.2.1 Determination of material constants for Arrhenius model

The material constants of constitutive equations were obtained from the experimental result from the hot compression test under different temperatures and strain rates. It has been found that the deformation strain effect on the flow stress will not be considered in Eqs. (6) and (7). In this research, it has been afforded to consider the influence of strain on the material constants of developed constitutive equations. As an example, the continuation is the estimate process of material constants at the deformation strain of 0.1. For the low-stress level (ασ<0.8) and high-stress level (ασ>1.2), replacing appropriate function into Eq. (8) leads to Eqs. (9) and (10), respectively.

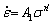                                (9)

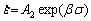                          (10)

where A₁ and A₂ are the material constants, which are not dependent on the deformation temperatures. Equations (11) and (12) can be obtained by taking the logarithm of both sides of Eqs. (9) and (10), respectively.

                     (11)

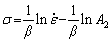                       (12)

Then, substituting the strain rate and corresponding true stress values under the strain of 0.1 into Eqs. (11) and (12) yields the linear relationship in the form of the straightforward and parallel lines in deforming conditions, as shown in Fig. 8. At a constant deformation temperature, the partial differentiation of Eqs. (11) and (12) gives the following equations, respectively:

                           (13)

                           (14)

where the values of n′ and β can be acquired from the slope of every single line in the ln σ - and σ - plots at the constant temperature by linear fit method, respectively (Figs. 8(a) and (b)).

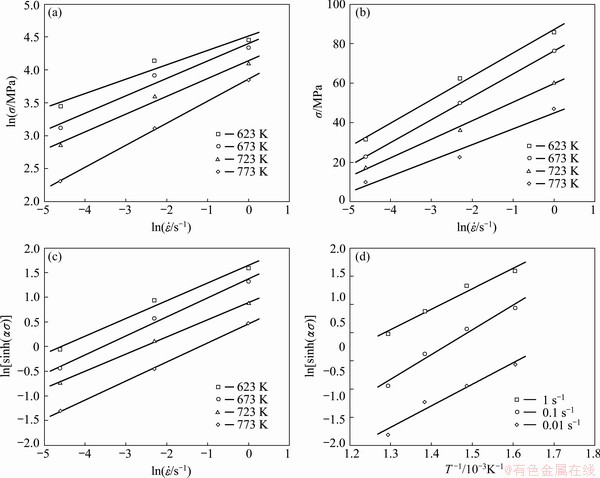
Fig. 8 Determination of n′ from slope of straight lines of ln σ -(a), β from slope of straight lines of σ - (b), n from slope of straight lines of ln[sinh(ασ)]-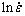(c) and Q from slope of straight lines of ln[sinh(ασ)]-1/T (d)

For the entire range of stress levels (containing low and high-stress levels), Eq. (7) can be represented as follows:

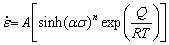               (15)

Equation (16) can be obtained by catching the natural logarithm of Eq. (15).

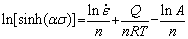            (16)

Differentiating Eq. (16) yields:

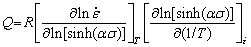    (17)

For special deformation temperature, differentiating Eq. (17) arrive to

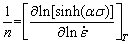                    (18)

The n value can be obtained by averaging from the slopes of the lines in ln[sinh(ασ)] -at constant deformation temperature, as shown in Fig. 8(c). In the same way and with considering Eq. (18), for a specific value of strain rate, differentiating Eq. (19) supplies

                  (19)

So, by replacing the values of deformation temperatures and flow stresses (under the strain of 0.1) obtained at a particular strain rate into Eq. (19), the value of Q can be taken from the slope of plotting ln[sinh(ασ)] versus 1/T, as shown in Fig. 8(d).

For all levels of stress, Eq. (16) can be represented as follows:

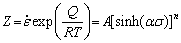             (20)

Catching the natural logarithm of Eq. (20), yields

ln Z=ln A+nln[sinh(ασ)]                   (21)

The relationship between ln[sinh(ασ)] and ln Z is presented in Fig. 9 with considering the experimental results. Then, the values of ln A and n are the intercept and slope of the straight line in ln Z-ln[sinh(ασ)] plot, respectively.

Finally, all of the material constants based on the Arrhenius-type model, i.e., n, β, α, n′, Q and A at strain of 0.1 can be calculated for AA7022-T6, and the results are shown in Table 3.

Fig. 9 Relationship between ln[sinh(ασ)] and ln Z

Table 3 Material constants based on Arrhenius-type model

4.2.2 Compensation of strain

Variation of the flow behavior of studied alloy with strain is evident in the true stress-true strain curves as shown in Fig. 3. However, the effect of strain should be taken into all of the material constants of the Arrhenius equation to predict more accurate flow stress.

The material constants of the Arrhenius equation can be obtained by polynomial fitting to establish the relationships among Q, lnA, n, α, and the true strain values from 0.1 to 0.6 in increment of 0.05. the influence of strain on the material constants is shown in Fig. 10. A sixth-order polynomial was found to represent the relationship between the strain and material constants, as expressed in Eq. (22).

 (22)

Fig. 10 Relationships among α, n, lnA and Q with true strain by polynomial fit of AA7022 alloy

After the estimation of the material constants of equations, the flow stress at a specific strain can be presented as a function of the Zener–Hollomon parameter (Z).

Once the material constants are estimated, the flow stress at an especial strain can be written as a function of the Zener–Hollomon parameter (Z). Therefore, the deformation behavior of AA7022-T6 at elevated temperature can be predicted by Eq. (23) that this developed constitutive equation correlates flow stress to Z with considering the Eqs. (6) and (15).

            (23)

Figure 11 shows the predicted results of strain compensated Arrhenius-type model and experimental flow stress curves of AA7022-T6. A comparison between the experimental results and the flow stress predicted by the strain-dependent constitutive equation indicates well conformity.

Fig. 11 Comparison between experimental and predicted flow stress curves by strain compensated Arrhenius-type model of AA7022 alloy at strain rates of 0.01 s^-1 (a), 0.1 s^-1 (b) and 1 s^-1 (c)

5 Verification of developed constitutive models

Predictability of the developed constitutive model for AA7022-T6 alloy has been evaluated by standard statistical methods consisting of correlation coefficient (r), average relative error (ARE) and root mean square error (RMSE) which are expressed as Eqs. (24)-(26), respectively.

               (24)

               (25)

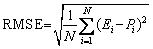                 (26)

where E_i is the experimental flow stress, P_i is the predicted flow stress achieved from the proposed constitutive models, 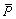 and 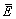 are the average values of P_i and E_i, respectively, and N is the number that was applied in the research.

The stresses predicted by constitutive models are plotted against the experimental results in Fig. 12. The values of r, ARE and RMSE for the modified J-C model are 0.9914, 6.074% and 10.611 MPa, respectively. The r, ARE and RMSE are 0.9972, 4.465% and 1.665 MPa, respectively for the strain compensated Arrhenius model. The correlation analysis indicates a good prediction accuracy of the strain compensated Arrhenius model to estimate the flow stress of the studied AA7022-T6 alloy.

Fig. 12 Correlation between experimental and predicted stresses by modified J-C model (a) and strain compensated Arrhenius-type model (b)

Also, the estimability of both the developed models has been investigated by statistical analysis of the relative error analysis. The relation of relative error (e_r) can be expressed as follows:

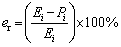                     (27)

The relative error results of both models are presented in Fig. 13. The variation of relative error is -8.36087% to 16.779% with mean relative error of 4.206%, and for the J-C model it varies from -15.478% to 10.136% with mean relative error of -0.2187% for the Arrhenius model.

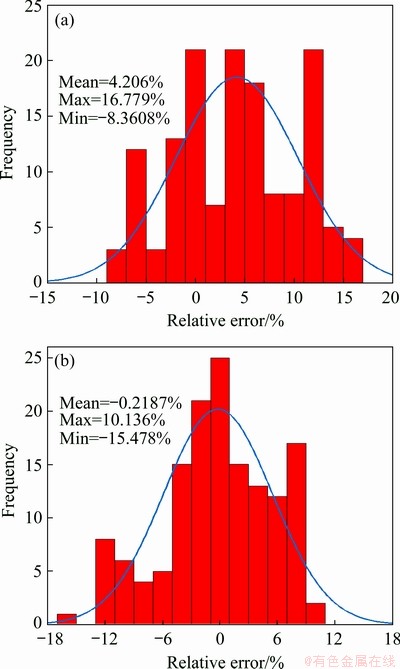
Fig. 13 Relative error analysis by modified J-C model (a) and strain compensated Arrhenius-type model (b)

6 Conclusions

(1) The flow stress behavior of the AA7022-T6 alloy is very dependent on hot deformation conditions such as strain rate, temperature and strain. Increasing the strain rate increases the flow stress while increasing the temperature produces the reverse effect.

(2) The true stress-true strain curves were modified by the correction of interfacial friction effects, so that, the predicted frictionless flow stress or corrected flow stress was used in the true stress-true strain curves.

(3) The microstructural investigations of deformed alloy indicated that dynamic recrystallization (DRX) was a main hot deformation mechanism at elevated temperatures and fine grains were observed along the deformed grain boundaries and grain interior.

(4) Both constitutive equations developed based on the modified J-C and strain compensated Arrhenius models can explain the flow behavior of AA7022-T6 alloy at elevated temperature. Although, the strain compensated Arrhenius model represents better accuracy than the modified J-C model.

(5) The predictability of two constitutive models was measured by its correlation coefficient, ARE and RMSE. The results showed that for the strain compensated Arrhenius-type and modified J-C developed models, the ARE values are 4.465% and 6.074%, respectively, and also the RMSE values are 1.665 and 10.611 MPa respectively, while the r values are 0.9972 and 0.9914, respectively. These results show that the strain compensated Arrhenius-type model can more exactly describe the hot deformation behavior of AA7022-T6 alloy.

References

[1] XIAO Wen-chao, WANG Bao-yu, WU Yong, YANG Xiao-ming. Constitutive modeling of flow behavior and microstructure evolution of AA7075 in hot tensile deformation [J]. Materials Science and Engineering A, 2018, 712: 704–713.

[2] SUN Zhi-Chao, ZHENG Li-Shuang, YANG He. Softening mechanism and microstructure evolution of as-extruded 7075 aluminum alloy during hot deformation [J]. Materials Characterization, 2014, 90: 71–80.

[3] CHEN Song-yi, CHEN Kang-hua, JIA Le, PENG Guo-sheng. Effect of hot deformation conditions on grain structure and properties of 7085 aluminum alloy [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 329–334.

[4] ZHANG Hong-ming, CHEN Gang, CHEN Qiang, HAN Fei, ZHAO Zu-de. A physically-based constitutive modelling of a high strength aluminum alloy at hot working conditions [J]. Journal of Alloys and Compounds, 2018; 743: 283–293.

[5] LIN Y C, LI Lei-ting, XIA Yu-chi, JIANG Yu-qiang. Hot deformation and processing map of a typical Al–Zn–Mg–Cu alloy [J]. Journal of Alloys and Compounds, 2013, 550: 438–445.

[6] WEN Dong-xu, LIN Y C, ZHOU Ying. A new dynamic recrystallization kinetics model for a Nb containing Ni–Fe–Cr-base superalloy considering influences of initial δ phase [J]. Vacuum, 2017, 141: 316–327.

[7] WU B, LI M Q, MA D W. The flow behavior and constitutive equations in isothermal compression of 7050 aluminum alloy [J]. Materials Science and Engineering A, 2012, 542: 79-87.

[8] LI Jiang, LI Fu-guo, CAI Jun, WANG Rui-ting, YUAN Zhan-wei, XUE Feng-mei. Flow behavior modeling of the 7050 aluminum alloy at elevated temperatures considering the compensation of strain [J]. Material and Design, 2012, 42: 369-377.

[9] ZHAO Jiu-hui, DENG Yun-lai, TAN Jia, ZHANG Jin. Effect of strain rate on the recrystallization mechanism during isothermal compression in 7050 aluminum alloy [J]. Materials Science and Engineering A, 2018, 734: 120-128.

[10] LIN Y C, CHEN Ming-song, ZHONG Jue. Prediction of 42CrMo steel flow stress at high temperature and strain rate [J]. Mechanics Research Communications, 2008, 35: 142-150.

[11] ADARSH S H, SAMPATH V. Hot deformation behavior of Fe–28Ni–17Co-11.5Al-2.5Ta-0.05B (at.%) shape memory alloy by isothermal compression [J]. Intermetallics, 2019, 115: 106632.

[12] QUAN Guo-zheng, SHI Rui-ju, ZHAO Jiang, LIU Qiao, XIONG Wei, QIU Hui-min. Modeling of dynamic recrystallization volume fraction evolution for AlCu4SiMg alloy and its application in FEM [J]. Transactions of Nonferrous Metals Society of China, 2019, 29: 1138-1151.

[13] ZHANG Er-lin, GE Yang, QIN Gao-wu. Hot deformation behavior of an antibacterial Co-29Cr-6Mo-1.8Cu alloy and its effect on mechanical property and corrosion resistance [J]. Journal of Materials Research and Technology, 2018, 34: 523-533.

[14] AASHRANTH B, SAMANTARAY D, KUMAR S, DASGUPTA A, BORAH U, ALBERT S K, BHADURI A K. Flow softening index for assessment of dynamic recrystallization in an austenitic stainless steel [J]. Journal of Materials Engineering and Performance, 2017, 26: 3531-3547.

[15] ZHANG Hong-jun, LI Chong, LIU Yong-chang, GUO Qian-ying, LI Hui-jun. Precipitation behavior during high-temperature isothermal compressive deformation of Inconel 718 alloy [J]. Materials Science and Engineering A, 2016, 677: 515-521.

[16] REZAEI ASHTIANI H R, SHAHSAVARI P. Strain- dependent constitutive equations to predict high temperature flow behavior of AA2030 aluminum alloy [J]. Mechanics of Materials, 2016, 100: 209-218.

[17] JI Cheng, WANG Zi-lin, WU Chen-hui, ZHU Miao-yong. Constitutive modeling of the flow stress of GCr15 continuous casting bloom in the heavy reduction process [J]. Metallurgical and Materials Transactions B, 2018, 49: 767-782.

[18] SOUZA P M, BELADI H, SINGH R P, HODGSON P D, ROLFE B. An analysis on the constitutive models for forging of Ti6Al4V alloy considering the softening behavior [J]. Journal of Materials Engineering and Performance, 2018, 27: 3545-3558.

[19] LIN Y C, LUO Shun-cun, JIANG Xing-you, TANG Yi, CHEN Ming-song. Hot deformation behavior of a Sr-modified Al-Si-Mg alloy: Constitutive model and processing maps [J]. Transactions of Nonferrous Metals Society of China, 2018, 28: 592-603.

[20] YANG Yan, PENG Xia-dong, REN Feng-juan, WEN Hai-ming, SU Jun-fei, XIE Wei-dong. Constitutive modeling and hot deformation behavior of duplex structured Mg-Li-Al-Sr alloy [J]. Journal of Materials Science & Technology, 2016, 32: 1289-1296.

[21] DING Xiao-feng, ZHAO Fu-qiang, SHUANG Yuan-hua, MA Li-feng, CHU Zhi-bing, ZHAO chun-jiang. Characterization of hot deformation behavior of as-extruded AZ31 alloy through kinetic analysis and processing maps [J]. Journal of Materials Processing Technology, 2020, 276: 116325.

[22] SUN Z C, WU H L, CAO J, YIN Z K. Modeling of continuous dynamic recrystallization of Al-Zn-Cu-Mg alloy during hot deformation based on the internal-state- variable (ISV) method [J]. International Journal of Plasticity, 2018, 106: 73-87.

[23] HUANG Chang-qing, DENG Jie, WANG Si-xu, LIU Lei-lei. A physical-based constitutive model to describe the strain- hardening and dynamic recovery behaviors of 5754 aluminum alloy [J]. Materials Science and Engineering A, 2017, 699: 106-113.

[24] REZAEI ASHTIANI H R, SHAHSAVARI P. A comparative study on the phenomenological and artificial neural network models to predict hot deformation behavior of AlCuMgPb alloy [J]. Journal of Alloys and Compounds, 2016, 687: 263-273.

[25] LI Cheng-lin, NARAYANA P L, REDDY N S, CHOI Seong-Woo, YEOM Jong-Taek, HONGA Jae-Keun, PARKA Chan Hee. Modeling hot deformation behavior of low-cost Ti-2Al-9.2Mo-2Fe beta titanium alloy using a deep neural network [J]. Journal of Materials Science & Technology, 2019, 35(5): 907-916.

[26] XU Le, CHEN Liang, CHEN Gao-jin, WANG Mao-qiu. Hot deformation behavior and microstructure analysis of 25Cr3Mo3NiNb steel during hot compression tests [J]. Vacuum, 2018, 147: 8-17.

[27] HE Jian-li, CHEN Fei, WANG Bo, ZHU Luo-bei. A modified Johnson-Cook model for 10%Cr steel at elevated temperatures and a wide range of strain rates [J]. Materials Science and Engineering A, 2018, 715: 1-9.

[28] LI Hong-ying, LI Yang-hua, WANG Xiao-feng, LIU Jiao-jiao, WU Yue. A comparative study on modified Johnson Cook, modified Zerilli-Armstrong and Arrhenius-type constitutive models to predict the hot deformation behavior in 28CrMnMoV steel [J]. Material and Design, 2013, 49: 493-501.

[29] TRIMBLE D, O’DONNELL G E. Flow stress prediction for hot deformation processing of 2024Al-T3 alloy [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 1232-1250.

[30] LIN Y C, LI Qi-fei, XIA Yu-chi, LI Lei-ting. A phenomenological constitutive model for high temperature flow stress prediction of Al-Cu-Mg alloy [J]. Materials Science and Engineering A, 2012, 534: 654-662.

[31] CHEN Xing-rui, LIAO Qi-yu, NIU Yan-xia, JIA Wei-tao, LE Qi-chi, CHENG Chun-long, YU Fu-xiao, CUI Jian-zhong. A constitutive relation of AZ80 magnesium alloy during hot deformation based on Arrhenius and Johnson-Cook model [J]. Journal of Materials Research and Technology, 2019, 8(2): 1859-1869.

[32] BOBBILI R, MADHU V. Constitutive modeling of hot deformation behavior of high-strength armor steel [J]. Journal of Materials Engineering and Performance, 2016, 25: 1829-1838.

[33] TRIMBLE D, O’DONNELL G E. Constitutive modelling for elevated temperature flow behaviour of AA7075 [J]. Materials and Design, 2015, 76: 150-168.

[34] MAHESHWARI A K, PATHAK K K, RAMAKRISHNAN N, NARAYAN S P. Modified Johnson-Cook material flow model for hot deformation processing [J]. Journal of Materials Science, 2010, 45: 859-864.

[35] ZHANG Bing, SHANG Xiao-di, YAO Su, WANG Qiu-yu, ZHANG Zhi-juan, YANG Xiao-kang, CAI Jun, WANG Kuai-she. A comparative study on Johnson-Cook, modified Johnson-Cook, modified Zerilli-Armstrong and Arrhenius- type constitutive models to predict hot deformation behavior of TA2 [J]. High Temperature Materials and Processes, 2019, 38: 699-714.

[36] LIN Y C, CHEN Ming-song, ZHONG Jue. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel [J]. Computational Materials Science, 2008, 42: 470-477.

[37] OU Ling, NIE Yu-feng, ZHENG Zi-qiao. Strain compensation of the constitutive equation for high temperature flow stress of a Al-Cu-Li alloy [J]. Journal of Materials Engineering and Performance, 2014, 23: 25-30.

[38] LIU Lei, WU Yun-xin, GONG Hai, WANG Kai. Modification of constitutive model and evolution of activation energy on 2219 aluminum alloy during warm deformation process [J]. Transactions of Nonferrous Metals Society of China, 2019, 29: 448-459.

[39] REZAEI ASHTIANI H R, PARSA M H, BISADI H. Constitutive equations for elevated temperature flow behavior of commercial purity aluminum [J]. Materials Science and Engineering A, 2012, 545: 61-67.

[40] LI Bo, PAN Qing-lin, YIN Zhi-min. Characterization of hot deformation behavior of as-homogenized Al-Cu-Li-Sc-Zr alloy using processing maps [J]. Materials Science and Engineering A, 2014, 614: 199-206.

[41] CHEN Bin, TIAN Xiao-lin, LI Xiao-ling, LU Chen. Hot deformation behavior and processing maps of 2099 Al-Li alloy [J]. Journal of Materials Engineering and Performance, 2014, 23: 1929-1935.

[42] MOSTAFAEI M A, KAZEMINEZHAD M. Hot deformation behavior of hot extruded Al-6Mg alloy [J]. Materials Science and Engineering A, 2012, 535: 216-221.

[43] NAYAK K C, DATE P P. Development of constitutive relationship for thermomechanical processing of Al-SiC composite eliminating deformation heating [J]. Journal of Materials Engineering and Performance, 2019, 28: 5323-5343.

[44] DAI Qing-song, DENG Yun-lai, TANG Jian-guo, WANG Yu. Deformation characteristics and strain-compensated constitutive equation for AA5083 aluminum alloy under hot compression [J]. Transactions of Nonferrous Metals Society of China, 2019, 29 (11): 2252-2261.

[45] LIU Shu-hui, PAN Qing-lin, LI Hang, HUANG Zhi-qi, LI Kuo, HE Xin, LI Xin-yu. Characterization of hot deformation behavior and constitutive modeling of Al-Mg-Si-Mn-Cr alloy [J]. Journal of Materials Science, 2019, 54: 4366-4383.

[46] SHI Cang-ji, MAO Wei-min, CHEN X-grant. Evolution of activation energy during hot deformation of AA7150 aluminum alloy [J]. Materials Science and Engineering A, 2013, 571: 83-91.

[47] ZHOU L, CUI C, WANG Q Z, LI C, XIAO B L, MA Z Y. Constitutive equation and model validation for a 31 vol.% B₄Cp/6061Al composite during hot compression [J]. Journal of Materials Science & Technology, 2018, 34(10): 1-9.

[48] DONG Yuan-yuan, ZHANG Cun-sheng, ZHAO Guo-qun, GUAN Yan-jin, GAO An-jiang, SUN Wen-chao. Constitutive equation and processing maps of an Al-Mg-Si aluminum alloy: Determination and application in simulating extrusion process of complex profiles [J]. Material and Design, 2016, 92: 983-997.

[49] ZHANG Cun-sheng, WEN Ming-yue, ZHAO Guo-qun, CHEN Liang, SUN Wen-chao, BAI Kai. One-time determination of 20 material parameters in a strain- compensated constitutive model and its application in extrusion for an Al-Zn-Mg thin-walled profile [J]. Thin-Walled Structuers, 2019, 135: 65-77.

[50] GHOLAMZADEH A, KARIMI TAHERI A. The prediction of hot flow behavior of Al-6%Mg alloy [J]. Mechanics Research Communications, 2009, 36: 252-259.

[51] LIN Y C, CHEN Xiao-min, LIU Ge. A modified Johnson-Cook model for tensile behaviors of typical high-strength alloy steel [J]. Materials Science and Engineering A, 2010, 527(26): 6980-6986.

[52] SELLARS C M, McTEGART W J. On the mechanism of hot deformation [J]. Acta Metallurgica, 1966, 14: 1136-1138.

[53] ZENER C, HOLLOMON J H. Effect of strain rate upon plastic flow of steel [J]. Journal of Applied Physics, 1944, 15: 22-32.

析出硬化AA7022-T6铝合金高温流变行为的本构模型

H. R. REZAEI ASHTIANI, P. SHAHSAVARI

School of Mechanical Engineering, Arak University of Technology, Arak, Iran

摘  要：在温度623~773 K和应变速率0.01~1 s^-1条件下，采用等温压缩试验研究析出硬化AA7022-T6 铝合金的热力学行为。结果表明，动态再结晶是主要的热变形机制，特别是在高温和低应变速率下。采用改进的Johnson- Cook (J-C)模型和应变补偿Arrhenius模型预测不同变形条件下的热流变行为。这两种模型的线性相关系数分别为0.9914和0.9972，平均相对误差(ARE)分别为6.074%和4.465%，均方根误差(RMSE)分别为10.611和1.665 MPa。结果表明，应变补偿Arrhenius模型能准确预测AA7022-T6铝合金的热流变应力。

关键词：流变行为；本构模型；Arrhenius模型；动态再结晶；AA7022-T6 铝合金

(Edited by Xiang-qun LI)

Corresponding author: H. R. REZAEI ASHTIANI; Tel: +98-86-33400671; Fax: +98-861-3670020; E-mail: hr_rezaei@arakut.ac.ir,

 hrr.Ashtiani@gmail.com

DOI: 10.1016/S1003-6326(20)65432-2