W/Cu梯度功能材料板稳态热应力分析
陶光勇, 郑子樵, 刘孙和
(中南大学 材料科学与工程学院, 长沙 410083)
摘 要: 采用解析法研究了W/Cu 梯度功能材料板的残余热应力和在稳态梯度温度场下的工作热应力的大小和分布状况。 结果表明: 随着成分分布指数的增加, 残余热应力与工作热应力的最大值先减小后增大, 当成分分布指数(P)取1时, 达到最小值; 随着梯度层数的增加, 热工作热应力的最大值逐渐减小, 但当梯度层数达到6时, 随着梯度层数的增加, 缓和效果并不明显; 当梯度层厚度增加到5mm时, 工作热应力的最大值约为非梯度材料工作热应力最大值的50%。
关键词: W/Cu梯度功能材料; 温度场; 热应力 中图分类号: TB33; TL62
文献标识码: A
Analysis of steady thermal stress in plate of W/Cu functionally graded material
TAO Guang-yong, ZHENG Zi-qiao, LIU Sun-he
(School of Materials Science and Engineering,Central South University, Changsha 410083, China)
Abstract: The residual thermal stress and the steady working thermal stress in the plate of W/Cu functionally graded material were analyzed by the analytical solution. The numerical results show that the compositional exponent (P), the number of layers(n) and the thickness of graded layer(hFGM) have significant effects on the thermal stress. The thermal stress can be mitigated effectively when P is 1 and n is 6. Compared with the Non-FGM, the maximum working thermal stress of FGM is reduced by 50% when hFGM is 5mm.
Key words: W/Cu functionally graded material; temperature field; thermal stress
在众多作为偏滤器和第一壁的候选材料当中, 钨由于其高的自溅射阀值(约200eV)、 高熔点、 高的高温强度和耐等离子体冲刷等性能而成为首选材料[1-4]。 在聚变堆反应的过程中, 由于与等离子体的作用, 钨的表面温度很高, 为了使反应堆整体能够良好地运转, 产生的热量必须及时地散发出去。 而铜具有优良的导热性能, 因此钨铜复合材料的研究成为当前的热点。 由于钨与铜的热物理性能相差很大, 若将钨与铜直接结合组成一种复合材料, 则会在结合面上产生很大的热应力而导致裂纹的产生, 缩短材料的工作寿命甚至失效。 钨铜梯度功能材料(以下简称W/Cu FGM)连续改变材料的组成和结构, 使其内部界面消失, 则能够很好的缓和热应力, 因此缓和热应力型的W/Cu FGM便成为解决这一问题的有效途径。 由于W/Cu FGM工作的环境较为苛刻, 工作产生的热应力和制备产生的残余热应力对其寿命和性能有着重大的影响, 因此分析W/Cu FGM的热应力场及其优化具有十分重要的意义。
目前对W/Cu FGM热应力的研究主要是采用有限元法[5-9], 而有限元法是以离散数学为基础, 它的结果只能是近似解。 对于几何形状比较规则且仅一维梯度的物理模型, 采用解析法避免了大量的计算且提供了精确的结果。 本文作者基于热弹性力学和辛谱生法, 对板状的W/Cu FGM制备时产生的残余热应力和工作时产生的热应力大小和分布进行研究, 找出W/Cu FGM的合理的成分分布指数、 梯度层数和梯度层厚度。
1 分析模型
由W和Cu 组成的FGM无限自由长板在稳态温度场的模型如图1所示。 在进行工作热应力分析时采用如下假设: 1) 材料的物理性能各向同性, 不随温度变化而改变, 材料无塑性变形; 2) 该板周边绝热, 其内部无内热源。 该板各层的厚度和坐标选择如图1所示。

图1 分析模型示意图
Fig.1 Schematic diagram of analytic model
T1(z)、 T2(z)、 T3(z)分别为纯铜层、 梯度层和纯钨层的温度分布函数, Z1、 Z2分别为纯铜层与梯度层、 梯度层与纯钨层的界面坐标, Z3为纯钨层端面坐标。
2 热应力分析
2.1 梯度组分分布函数和物性参数的估算
FGM由W和Cu构成, 体积分别为φW和φCu, 则:
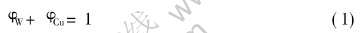
梯度组分分布采用如下函数表示:
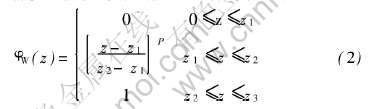
式中 P为成分分布指数, 决定着函数φW(z)的曲线走向, 即钨成分沿梯度方向变化的快慢。
本研究以W为基体、 Cu为弥散相, FGM的任一位置z处的物性参数根据Reuss法则[7]计算, 如下所示:

式中 E(z)、 α(z)、 λ(z)、 v(z)和K分别为弹性模量、 线膨胀系数、 热导率、 泊松比和体弹性模量, Cg为经验常数。
2.2 应力分析
采用叠层和熔渗等工艺制备W/Cu梯度功能材料时, 在制备过程中由高温冷却到室温时, 由于较大的温差和各微层之间热物理性能的差异, 导致在梯度材料内部产生残余热应力。 本研究设W/Cu FGM经历的温度差△T=1330K, 即从1350℃无应力状态冷却到室温。
W/Cu FGM作为核聚变反应堆的偏滤器, 表面工作温度达到1300K[10]左右。 为了使产生的热量能及时地散发, 铜侧必须强制冷却致低温(300K), 在梯度温度场中由于W与Cu之间物性参数的悬殊便产生了工作热应力。
为求解梯度层中的工作热应力分布函数σ(z), 首先要求出梯度材料的热传导方程与温度分布函数T(z)。 热传导率λ(z)沿厚度方向按式(5)变化, 沿厚度方向的一维热传导方程为

引入边界条件:
z=0, Ta=300K
z=1, Tb=1300K
为计算的方便,z为无因次坐标, z=Z/h。 根据式(7), 求得:
纯铜层的温度分布
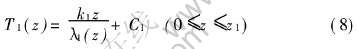
梯度层的温度分布

纯钨层的温度分布

由温度场的连续性根据式(8)、 (9)、 (10) 求得:

在梯度层内各点应力可认为是平面应力, 由于W/Cu FGM板的每一微层是均匀的各向同性体, 所以在每一层上有
εx=εy=ε(z), σx=σy=σ(z)
由热弹性方程、 应力与应变的关系[11-13], 在相等的双轴应力状态(Lyh, Lxh)下求得板内工作热应力的分布为

式中 T0为梯度层处于无压力状态时的初始温度; ε0、 ρ为分别为变形后板下表面的应变分量和曲率。 当T(z)为常数时, 所求解σ(z)为制备的残余热应力; 当T(z)为变数时, 所求解为σ(z)为工作热应力。
在纯热载荷的条件下, ε0、 ρ可由梯度层的内应力和弯曲力矩的平衡条件[14, 15]求出, 即:

根据式(13)和(14)求得:

根据W/Cu FGM为颗粒复合材料的实际情况, W在W/Cu复合材料中是连续的而Cu是非连续相。 根据Halpin-Tsai方程[13], 因为W/Cu FGM板内各向同性, 在纯热载荷的作用下, 利用应力-应变关系, 当εx=εy、 εz=0时, 基体W的热应力为:
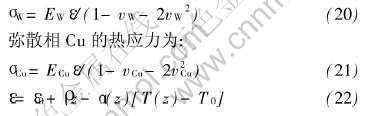
3 结果与讨论
3.1 成分分布指数对热应力的影响
不同的P值使得过渡层的物性参数有不同的过渡方式, 因而造成热应力的不同分布。 以hCu=hW=1mm, 梯度层数n=4为例, 讨论成分分布指数P对热应力的影响。 图2所示为热应力随不同成分分布指数的分布。
从图2中看出, 随着P的增大, 工作热应力曲线与残余热应力曲线位置发生变化。 这主要是由混合物性参数的改变造成的, 残余热应力的值比工作热应力的值大得多。 随着P值的增加, 残余热应力的最大值的位置从富铜端转到富钨端, 而工作热应力的位置基本不变, 总是出现在富钨端。 随着P的增大, 梯度层的物性参数的最大差别区域向富钨端转移, 由于残余热应力在均匀温度场中产生, 热应力的分布受温度影响较小, 主要由物性参数决定, 因而残余热应力的最大值的位置从富铜端转向富钨端。 工作热应力不仅受到物性参数的影响, 还受到梯度温度场的制约。 当P值较小时, 物性的最大差别区域在富铜端, 但富铜端温度较低, 且铜的热导率较高, 温度趋于均匀, 使得不同的梯度层间温差较小。 而富钨端温度较高, 弹性模量大, 不利于热应力的释放, 综合以上因素, 工作热应力的最大值总是出现在富钨端。 FGM各层物性参数的不同, 热膨胀系数小的一侧材料的热膨胀小, 另一侧的热膨胀较大。 但由于材料的连续性, 热膨胀小的一侧受到拉动而变形增大, 热膨胀大的一侧受到束缚而变形减小并达到整体平衡, 于是在各层的界面上产生了应力差。 从图中可看出工作热应力的最大差值总是出现在纯钨层与梯度层的结合面上, 而残余热应力的最大应力差值发生的位置是逐渐变化的, 由纯铜层与梯度层的结合面向纯钨层与梯度层的结合面转移。 当P=0.5时, 梯度层间的应力差值较大, 而P=1.0时, 相差程度相对较小, 当P大于1.0时, 变化程度又增大。

图2 热应力随成分分布指数变化曲线
Fig.2 Thermal stress curves with different compositional exponents (P)
上述的计算结果与文献[10]报道的残余热应力的变化趋势相同而与工作热应力的变化不同, 原因可能是文献[10]在对物性参数的估算时采用较为简单的混合法则。 在复合材料中, 当一相是非连续的, 而另一相是连续的基体时, 简单的混合法则与复合材料的有效物性相差较大[13]。 文献[9]报道的热应力过渡趋势较为光滑, 可能是在采用有限元求解时网格划分较少, 但在P值对热应力的影响上与其报道的基本吻合。
由图3中可看出, Cu相的热应力比W相的小。 在成分分布指数相同的情况下, Cu相的热应力沿厚度方向的分布较均匀, 这主要是由于Cu的弹性模量较小, 其应力因变形容易得到释放。
从图4中可以看出, 工作热应力和残余热应力的最大值的变化走向基本一致, 先减小后增大, 在P=1时有最小值。 当P值较小时, 物性值在富铜端出现急剧的变化, 当P值较大时, 物性值在富钨端出现急剧的变化, 而当P=1.0时, 物性值的过渡一直较为平缓。
3.2 梯度层数n对热应力分布的影响
以hCu=hW=1mm、 P=1.0为例, 讨论梯度层数n对热应力分布的影响。
图5所示为工作热应力随不同梯度层数n的分布曲线。 从图中可以看出, 当成分分布指数P=1.0时, 不同梯度层的热应力变化趋势基本相同, 在富铜端受到压应力, 梯度层受到拉应力, 在富钨端转成压应力, 变化点出现在纯铜与梯度层和梯度层与纯钨的过渡区, 在纯铜端由于热膨胀系数较大, 而在第二层膨胀系数较小, 故纯铜端受到压应力; 而在富钨端尽管膨胀系数较小, 但温度较高, 且由于弹性模量相差较大, 于是受到压应力。 随着梯度层数的增加, 热应力的变化程度变得平缓, 即梯度层间热应力的差值变小。
图6所示为最大工作热应力随梯度层数的变化曲线, 从图中看出随着梯度层数的增加, 热应力的

图3 W、 Cu工作热应力随成分指数和无因次坐标变化等值曲线图
Fig.3 Contours of working thermal stress of W and Cu with different compositional exponents (P) and nondimensional coordinate (z)

图4 最大热应力随分布指数的变化曲线
Fig.4 Curves of maximum thermal stress with different compositional exponents (P)

图5 不同梯度层数的工作热应力的分布曲线
Fig.5 Curves of working thermal stress with different layers
最大值逐渐变小, 梯度层数的增多, 使得成分过度更加均匀, 梯度层的物性参数得以缓慢的过渡, 减小界面的应力集中。 当梯度层达到6层时, 最大值降为2层的50%, 且梯度层继续增多时, 变化趋势变得平缓, 而文献[9]所报道的当层数达到4时热应力的变化趋势随层数的增多并不明显。 由于在各层的界面上会出现应力的急剧变化, 使用有限元法时如果在界面处网格划分较少, 得出的值变化相对较小; 另一方面, 文献[9]在对热导率的计算上采用的是W/Cu FGM整体的当量热导率, 因而使得各微层的温度易于趋于均匀, 层间的热应力变化趋势变得缓和。 在由纯Cu端过渡到纯W端时, 热导率是逐渐变化的。 实际上, 当层数为4时, 各层之间的物性仍然相差较大。

图6 最大工作热应力随梯度层数的变化曲线
Fig.6 Curve of maximum thermal working stress with different layers
3.3 梯度层厚度对热应力的影响
以hCu=hW、 P=1.0、 n=4为例, 讨论梯度层厚度对热应力的影响。
图7所示为工作热应力随梯度层厚度变化的分布曲线。 从图中可看出, 随着梯度层厚度的增加, 最大热应力的位置从中部向富钨端转移。 当hFGM=0mm, 即非梯度功能材料(简称NFGM), 在钨与铜的结合面上应力出现急剧的变化; 随着hFGM的增加, 成分分布得以细化, 物性参数的过渡更加平滑, 应力的变化趋势变得缓和。

图7 不同梯度层厚度的工作热应力分布曲线
Fig.7 Curves of working thermal stress with different thicknesses
图8所示为最大工作热应力随梯度层厚度的变化曲线。 从图中可看出, 随着梯度层厚度的增加, 最大热应力值逐渐减小。 当hFGM=5mm时, 工作热应力最大值降为NFGM最大值的50%; 梯度层厚度较小时, 随着hFGM的增大, 热应力的最大值出现较大的变化, 说明hFGM的增加对缓和热应力有很好的效果。 当hFGM增大到一定值时, 最大值变化趋势变得缓和; 当hFGM=4mm后继续增大hFGM时, 该趋势进一步变缓的效果并不明显。
W/Cu FGM热应力的计算与讨论都是建立在两种组成相W和Cu的基础上, 而且材料从制备温度冷却到室温和在高温服役的过程中只经历弹性变形。 实际上, 低熔点金属Cu在高温下可能会发生
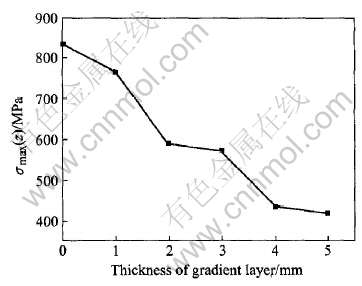
图8 最大工作热应力随梯度层厚度的变化曲线
Fig.8 Curve of maximum working thermal stress with thicknesses
塑性变形和低速蠕变, 而金属W虽然熔点很高, 但也可能会发生一些缓慢的自扩散, 这些都会导致材料在制备和服役过程中热应力的松弛, 使以上理论计算热应力的数值比实际值大。
4 结论
1) 当成分分布指数P=1时, 热应力的最大值达到最小, 梯度层间的热应力差值较为缓和, 成分分布指数取1对缓和热应力具有明显的作用。
2) 梯度层数对热应力的影响较大, 当梯度层数n≥6时, 对缓和热应力的效果较好, 为了制备的方便, 梯度层数取6即可有效地缓和热应力。
3) 梯度层的厚度hFGM越大, 对缓和热应力越有利, hFGM=5mm时, 工作热应力的最大值降为非梯度功能材料工作热应力的50% 。
REFERENCES
[1]WANG Bao-lin, MAI Yiu-wing. Thermal shock resistance of functionally graded materials[J]. Acta Materialia, 2004, 52: 4961-4972.
[2]Liu X, Yang L.Thermal response of plasma sprayed tungsten coating to high heat flux[J]. Fusion Engineering and Design, 2004, 70: 341-349.
[3]Bolt H, Barabash V, et al. Materials for the plasma-facing components of fusion reactors[J]. Journal of Nuclear Materials, 2004, 329-333: 66-73.
[4]ZHANG Ming, HUANG Hong-jun. Development of functionally gradient materials[J]. Materials Science Forum, 2002, 423-425: 599-600.
[5]Jin G, Nishikawa T, Honda S, et al. Stress analysis in multilayered FGM plate under thermal shock[J]. Materials Science Forum, 2003, 423-425: 693-698.
[6]LING Yun-han, BAI Xin-de, GE Chang-chun. Design and thermal shock performance of W/Cu functionally graded materials used as plasma facing component[J]. Materials Science Forum, 2003, 423-425: 49-54.
[7]Gasik M M. Micromechanical modeling of functionally graded materials[J]. Computational Materials Science, 1998, 13: 42-55.
[8]Ravichandran K S. Thermal residual stress in a functionally graded material system[J]. Mater Sci Eng A, 1995, A201: 269-276.
[9]凌云汉, 白新德, 葛昌纯. 偏滤器部件W/Cu功能梯度材料的热应力缓和[J]. 清华大学学报(自然科学版), 2003, 43(6): 750-753.
LIN Yun-han, BAI Xin-de, GE Chang-chun. Thermal stress reduction in a W/Cu functionally graded material used as a divertor component[J]. Journal of Tsinghua University, 2003, 43(6): 750-753.
[10]Itoh Y, Takahashi M, Takao H. Design of tungsten/copper graded composite for high heat flux components[J]. Fusion Engineering and Design, 1996, 31: 279-289.
[11]黄义. 弹性力学基础及有限单元法[M]. 北京: 冶金工业出版社, 1983. 17-20.
HUANG Yi. Foundation of Mechanics of Elasticity and Finite Element Method[M]. Beijing: Metallurgical Industry Press, 1983. 17-20.
[12]张开银, 张建刚, 吕运冰. 功能梯度材料复合板的热应力计算分析[J]. 湛江海洋大学学报, 1997, 17(1): 34-38.
ZHANG Kai-yin, ZHANG Jian-gang, LU Yun-bing. Thermal stress analysis in ceramic/metal functionally graded material plate[J]. Journal of Zhanjiang Ocean University, 1997, 17(1): 34-38.
[13]Suresh S, Mortensen A. 功能梯度材料基础—制备及热机械行为[M]. 北京: 国防工业出版社, 2000: 108-115.
Suresh S, Mortensen A. The Foundation of Functionally Graded Materials-preparation and Thermal Mechanical Behavior[M]. Beijing: National Defence Industry Press, 2000: 108-115.
[14]张晓丹, 戚国安, 汪朝霞, 等. 梯度功能材料热应力分析模型[J]. 应用科学学报, 1995, 13(2): 202-207.
ZHANG Xiao-dan, QI Guo-an, WANG Zhao-xia, et al. Mathematical model on the design of functionally gradient materials and thermal stress analysis of FGM plates[J]. Journal of Applied Sciences, 1995, 13(2): 202-207.
[15]李益民, 郑子樵, 梁叔全, 等. 梯度功能材料的组成设计分析[J]. 中国有色金属学报, 1995, 15(1): 55-59.
LI Yi-min, ZHENG Zi-qiao, LIANG Shu-quan, et al. The analysis of design and composition of functionally graded material[J]. The Chinese Journal of Nonferrous Metals, 1995, 15(1): 55-59.
(编辑何学锋)
收稿日期: 2005-07-13; 修订日期: 2005-09-06
通讯作者: 陶光勇, 电话; 0731-8830270; E-mail: taogy123@263.net