A unified prediction solution for vibro-acoustic analysis of composite laminated elliptical shells immersed in air
来源期刊:中南大学学报(英文版)2021年第2期
论文作者:秦斌 关先磊 钟锐 王青山 帅词俊
文章页码:429 - 444
Key words:composite laminated elliptical shells; semi-analytical method; vibration; sound radiation
Abstract: A semi-analytical method to conduct vibro-acoustic analysis of a composite laminated elliptical shell immersed in air is proposed. A variational method and multi-segment technique are used to formulate the dynamic model. The sound radiation of the exterior fluid field is calculated by a spectral Kirchhoff–Helmholtz integral formulation. The variables containing displacements and sound pressure are expanded by the combination of Fourier series and Chebyshev orthogonal polynomials. The collocation points are introduced to construct an algebraic system of acoustic integral equations, where these points are distributed on the roots of Chebyshev polynomials, and the non-uniqueness solution of system is eliminated by a combined Helmholtz integral. Numerical examples for sound radiation problems of composite laminated elliptical shells are presented and individual contributions of the circumferential modes to the acoustical results of composite laminated elliptical shells are also given. The effects of geometric and material parameters on sound radiation of composite laminated elliptical shells are also investigated.
Cite this article as: GUAN Xian-lei, ZHONG Rui, QIN Bin, WANG Qing-shan, SHUAI Ci-jun. A unified prediction solution for vibro-acoustic analysis of composite laminated elliptical shells immersed in air [J]. Journal of Central South University, 2021, 28(2): 429-444. DOI: https://doi.org/10.1007/s11771-021-4613-1.

J. Cent. South Univ. (2021) 28: 429-444
DOI: https://doi.org/10.1007/s11771-021-4613-1
GUAN Xian-lei(关先磊)1, ZHONG Rui(钟锐)1, QIN Bin(秦斌)1, 2, 3,WANG Qing-shan(王青山)1, SHUAI Ci-jun(帅词俊)1, 4
1. State Key Laboratory of High Performance Complex Manufacturing, Central South University,Changsha 410083, China;
2. Joint International Research Laboratory of Key Technology for Rail Traffic Safety,Central South University, Changsha 410075, China;
3. National & Local Joint Engineering Research Center of Safety Technology for Rail Vehicle,Central South University, Changsha 410075, China;
4. Institute of Bioadditive Manufacturing, Jiangxi University of Science and Technology,Nanchang 330013, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract: A semi-analytical method to conduct vibro-acoustic analysis of a composite laminated elliptical shell immersed in air is proposed. A variational method and multi-segment technique are used to formulate the dynamic model. The sound radiation of the exterior fluid field is calculated by a spectral Kirchhoff–Helmholtz integral formulation. The variables containing displacements and sound pressure are expanded by the combination of Fourier series and Chebyshev orthogonal polynomials. The collocation points are introduced to construct an algebraic system of acoustic integral equations, where these points are distributed on the roots of Chebyshev polynomials, and the non-uniqueness solution of system is eliminated by a combined Helmholtz integral. Numerical examples for sound radiation problems of composite laminated elliptical shells are presented and individual contributions of the circumferential modes to the acoustical results of composite laminated elliptical shells are also given. The effects of geometric and material parameters on sound radiation of composite laminated elliptical shells are also investigated.
Key words: composite laminated elliptical shells; semi-analytical method; vibration; sound radiation
Cite this article as: GUAN Xian-lei, ZHONG Rui, QIN Bin, WANG Qing-shan, SHUAI Ci-jun. A unified prediction solution for vibro-acoustic analysis of composite laminated elliptical shells immersed in air [J]. Journal of Central South University, 2021, 28(2): 429-444. DOI: https://doi.org/10.1007/s11771-021-4613-1.
1 Introduction
With the progress of science and technology and the improvement of the quality of life, more stringent requirements are put forward for the lightweight of the structure, that is, under the premise of meeting the structural strength, its weight should also be lighter. It is based on this background that fiber laminated materials emerge as the times require and are widely used in ship, aerospace, automobile and other engineering industries. As a basic bearing structure, the application scenarios of elliptical shells are various.
For the elliptical shells made of composite laminated materials, they will receive the vertical load excitation in the actual project, so they will also produce complex vibration and noise. For designers, it is of great significance to master its characteristics in the design stage to eliminate its shortcomings.
FRANCESCO and his team [1-6] studied the static, free vibration and transient dynamic response behavior of elliptical shells with classical boundary conditions. In their research, the materials used to prepare elliptical shells mainly included functional gradient ceramic materials [1-5], fiber laminated materials [3, 4], carbon nano materials[2] and so on. The vibration behavior of coupled doubly-curved revolution shell structures with general boundary conditions was studied by WANG et al [7, 8] using Jacobi-Ritz method. PANG et al [9-11] applied the Jacobi-Ritz method to study free vibration behavior of the uniform and step elliptical shells. YE et al [12, 13] applied the modified Ritz method to examine the vibration characteristics of composite laminated elliptical shells with elastic restraints. TALEBITOOTI and ANBARDAN [14] used the Haar wavelet discretization approach to examine the frequency analysis of the functionally graded elliptical shells. XIE et al [15] proposed a unified semi-analytical method to study free and forced vibrations of arbitrary shells of revolution stiffened by rings with T cross-section. On the basis of the first-order shear deformation theory, ZHEN et al [16] analyzed the vibration behavior of stiffened composite elliptical shell based on modified Ritz approach. The above is the research status of vibration characteristics of elliptical shells in recent years. Next, the current research on acoustic vibration characteristics of the shells will be summarized as follows. Based on truncated modal basis of the dry structure, BEROT et al [17] presented an analytical formulation and a numerical model to study the vibro-acoustic behavior of cylindrical thin shells. CARESTA and KESSISSOGLOU [18, 19] used power series solution and wave approach to study the structural and acoustic responses of a submarine cylindrical shell subject to harmonic force excitation. CHEN et al [20] used the double reflection method to study the vibro-acoustic characteristics of cylindrical shells with free surface and rigid wall surface acoustic boundary conditions. GUO [21] surveyed the sound radiation from cylindrical shells due to internal sources. In this paper, far-field solutions were examined in detail to identify dominant features in the radiation process, such as those controlling the frequency characteristics and the directivity pattern of the radiated field. ZOU et al [22, 23] proposed an analytical formulation to evaluate the underwater acoustic radiation of an infinite cylindrical shell containing an internal flexural floor on the basis of the reciprocity theorem. WANG et al [24] applied the experimental test and precise transfer matrix method to study the vibro-acoustic responses of the cylindrical shell structure with classical boundary conditions.
Through the investigation of the present situation of the vibration and acoustic response of laminated elliptical shells, it can be found that there are many researches on the vibration characteristics of laminated elliptical shells, but the acoustic response analysis is still very rare. As mentioned above, the acoustic response analysis is very important for the early design of laminated elliptical shells. This paper aims to present a general method to predict the sound radiation from a laminated elliptical shell immersed in air. A variational method and a multi-segment partitioning technique are combined to formulate the dynamic model based on the first-order shear deformation shell theory. The multi-segment partitioning technique was originally developed by the coauthors [8, 25], where the dynamic analysis of composite laminated doubly-curved shells of revolution is conducted. By dividing the shell into several segments along the meridian line, the orders of the Fourier series and Chebyshev orthogonal polynomials can be reduced to achieve enough accurate results, especially for high-frequency problems. A spectral Chebyshev Kirchhoff–Helmholtz integral formulation is adopted to express the exterior acoustic fluid. The displacement components of the laminated elliptical shell and the sound pressure of the acoustic field are expanded as a double mixed series of Fourier series and Chebyshev orthogonal polynomials, by which the two-dimensional integrals are reduced to one dimensional integral along the generator line of the shell. The non-unique frequency phenomenon in the solution process is avoided by the CHIEF method. Numerical examples are presented for laminated elliptical shells with different geometric parameters and materials immersed in air and subjected to different boundary conditions.
2 Theoretical formulations
2.1 Model description
A composite laminated elliptical shell shown in Figure 1 is studied. The shell with total thickness h is characterized by its reference surface generated by the rotation of the meridian curve about the revolution axis z. It should be pointed out that axis z′ denotes the geometric axis of the meridian curve and Rs is the offset of the revolution axis z with respect to the geometric axis z′. The cylindrical coordinate system (φ, θ, ζ) is fixed in the middle of elliptical shell. Symbolic variables φ, θ and ζ represent variables of elliptic shell in meridional direction, circumferential direction and thickness direction, respectively. The geometric parameters of elliptical caps are defined by the combination of curvature radius Rφ and curvature radius Rθ. According to Refs. [12, 13], their specific expressions are as follows:
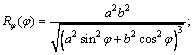
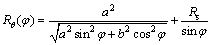 (1)
(1)
where a and b are the lengths of the semimajor and semiminor axes of the elliptic meridian, respectively.
In Figure 1, R0 is the horizontal radius representing the distance of the point on the reference surface from the revolution axis z, and R0=Rθsinφ.θ is the included angle between the material coordinate of the kth laminated layer and the φ-axis of shell. ζk and ζk+1 are distances from the bottom surface and the top surface of the kth layer to the reference surface, respectively.
2.2 Dynamic model
The dynamic model of the composite laminated elliptical shell can be established by the variational method and multi-segment technique proposed in Ref. [8-25]. This method is capable of modeling arbitrary composite laminated doubly- curved shells of revolution. For concise, the modeling process is not given here anymore; however, the derivations are presented since they are related to the present investigation directly. For a composite laminated elliptical shell being divided into Nφ segments in the meridional α direction, the energy functional may be derived as [8-25]:
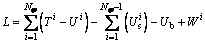 (2)
(2)
where Ti and Ui are the kinetic energy and strain energy, respectively; Wi is the virtual work done by mechanical forces acting on the shell segment; U i s is the interface potential on the common boundary between adjacent shell segments i and i+1; Ub is the boundary potential energy on the edges of composite laminated elliptical shell.
On the basis of the first-order shear deformation theory, the displacement components of the point in a composite laminated elliptical shell can be expressed by the displacements and rotations of the reference surface:
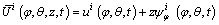 (3a)
(3a)
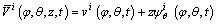 (3b)
(3b)
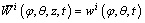 (3c)
(3c)
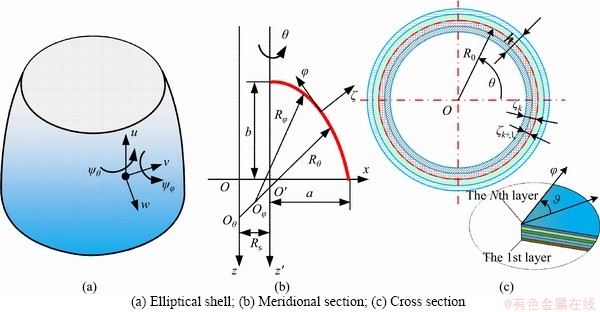
Figure 1 Coordinate system for elliptical shell:
where ui, vi and wi are the mid-plane displacements on the middle surface; ψi φ and ψi θ are the rotational displacements.
The following kinetic energy functions will be developed in segments. Based on FSDT, the strain energy and kinetic energy of ith segments are defined as:
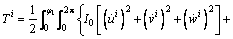
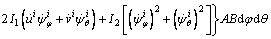 (4)
(4)
where the dot above the variables is the differential notation. And the concrete expression of mass stiffness coefficient I is as follows:
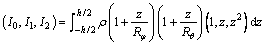 (5)
(5)
The strain energy for the ith shell segment is:
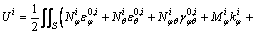
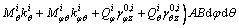 (6)
(6)
where ε0,i φ, ε0,i θ and γ0,i φθ are the membrane strains of the reference surface; ki φ, ki θ and ki φθ denote the curvature changes; γ0,i φz and γ0,i θz are the transverse shear strains. Ni φ, Ni θ and Ni φθ are the in-plane force resultants; Mi φ, Mi θ and Mi φθ represent the bending and twisting moment resultants; Qi φ and Qi θ are the transverse shear force resultants. The membrane strains and curvature of the reference surface are:
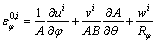 (7a)
(7a)
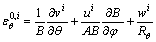 (7b)
(7b)
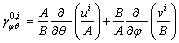 (7c)
(7c)
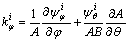 (7d)
(7d)
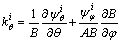 (7e)
(7e)
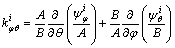 (7f)
(7f)
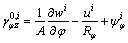 (7g)
(7g)
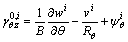 (7h)
(7h)
where A=Rφ, B=Rθsinφ. The force and moment resultants relations to the strains and change of curvatures are:
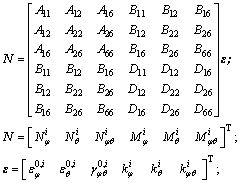
 (8)
(8)
where κ is the shear correction factor and it is set as 5/6 in this paper. The extensional stiffness Aij, the bending stiffness Dij and the extensional-bending coupling stiffness Bij are shown as respectively:
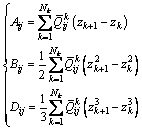 (9a)
(9a)
 (9b)
(9b)
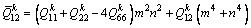 (9c)
(9c)
 (9d)
(9d)
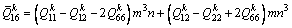 (9e)
(9e)
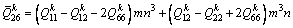 (9f)
(9f)
 (9g)
(9g)
 (9h)
(9h)
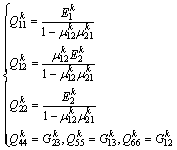 (9i)
(9i)
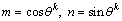 (9j)
(9j)
The boundary energy stored in the boundary end of elliptical shell can be described as:
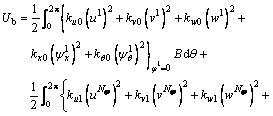
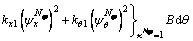 (10)
(10)
where ku, kv, kw, kφ and kθ respectively, denote the boundary stiffnesses. For two adjacent shell segments at each shell component, the potential energy stored in the connective springs is:
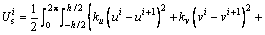

 (11)
(11)
The virtual work of the ith shell segment due to mechanical forces is:
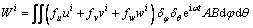 (12)
(12)
where δ is the Dirac function; δφ=δ(φ-φf), δθ=δ(θ-θf); fu, fv and fw are the distributed mechanical forces in the meridional, circumferential and the normal directions, respectively; e is natural exponent; i is an imaginary number and i2=-1; ω is circular frequency; t is time. In this paper, the displacement and rotation components are all generally expanded by Chebyshev orthogonal polynomials and Fourier series. On this basis, a 2D problem is transformed into a set of 1D problems and they are uncoupled, which correspond to the harmonics of the Fourier expansion. The displacement components of the ith shell segments can be written in the forms:
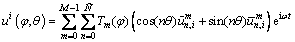 (13a)
(13a)
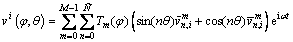 (13b)
(13b)
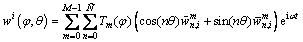 (13c)
(13c)
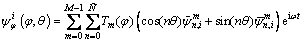 (13d)
(13d)
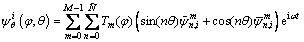 (13e)
(13e)
where M is the number of polynomial terms; Tm(φ) are the mth order Chebyshev orthogonal polynomials of the first kind; n is the circumferential wavenumber of the corresponding mode shape and it is a Non-negative integer;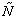 is the highest degree taken in the Fourier series;
is the highest degree taken in the Fourier series; 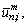
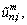
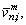
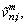
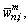
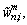
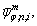
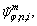
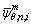 and
and  are the generalized displacement variables. Because the orthogonal Jacobi polynomials are defined on the interval φ∈[-1,1], so when using them in the interval φ (for the ith shell segment, φ∈[φi, φi+1]), a linear transformation should be made firstly, for each shell segment from φ∈[φi, φi+1] to φ∈[-1, 1].
are the generalized displacement variables. Because the orthogonal Jacobi polynomials are defined on the interval φ∈[-1,1], so when using them in the interval φ (for the ith shell segment, φ∈[φi, φi+1]), a linear transformation should be made firstly, for each shell segment from φ∈[φi, φi+1] to φ∈[-1, 1].
Substituting Eqs. (4), (6) and (10)-(13) into Eq. (2), the discretized motion equation yields
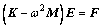 (14)
(14)
where E represents the generalized displacement Jacobi expanded coefficients; M and K are the total mass and stiffness matrices, respectively; F is the generalized force vector which is caused by the external structural excitation.
2.3 Acoustic model
The Kirchhoff–Helmholtz integral equation is used to express the acoustic field in a global cylindrical coordinate system (r, θ, z) in Figure 2, of which the original point O is set at the geometric center on the axis of shell considering the symmetries of elliptical shells. r is the direction of original point O pointing to the field point; θ is the circumferential direction and z is the axial direction. The sound pressure p(r) at a field point r(r, θ, z) can be written by the Kirchhoff-Helmholtz integral formulation as [26]:
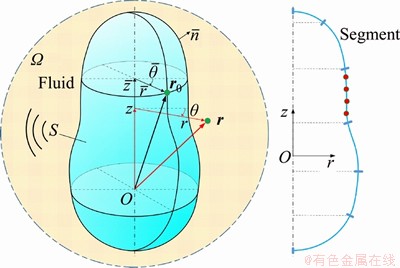
Figure 2 Coordinate system for acoustic field of structure
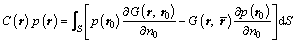 (15)
(15)
where r(r, θ, z) and r0(r0, θ0, z0) are the position vectors of field points, and they are exterior to and on the fluid-shell interface S, respectively;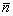 is the outward normal direction of any point on the shell surface, and
is the outward normal direction of any point on the shell surface, and  /
/ n0 represents the outward normal derivative with respect to the shell; C(r) is a coefficient depending on the position of the field point r(r, θ, z); G(r, r0) is the three-dimensional free space Green’s function:
n0 represents the outward normal derivative with respect to the shell; C(r) is a coefficient depending on the position of the field point r(r, θ, z); G(r, r0) is the three-dimensional free space Green’s function:
 (16)
(16)
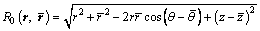 (17)
(17)
where k=ω/cf is the acoustic wave number, and cf is the sound speed in the fluid.
Due to the axisymmetry of the fluid-shell interface, the fluid field, in the circumferential direction, is expressed by the Fourier series, and by summing up them to a sufficient number of harmonics, the actual sound field is obtained. By this, the pressure of the acoustic field relative to the rotation angle is expanded by the Fourier series. The specific expressions are as follows:
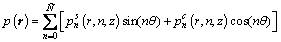 (18a)
(18a)
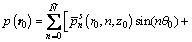
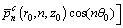 (18b)
(18b)
where ps n and pc n are pressure coefficients of the acoustic pressure at field point r;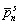 and
and 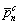 are those of the field point r0; n is the acoustic mode number in the circumferential direction. Similarly, the Green’s function and its normal derivative are:
are those of the field point r0; n is the acoustic mode number in the circumferential direction. Similarly, the Green’s function and its normal derivative are:
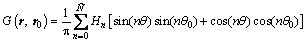 (19a)
(19a)
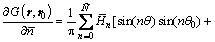
 (19b)
(19b)
in which
 ,
,
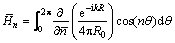 (20)
(20)
The normal displacement of shell on the shell-fluid interface, according to the momentum equation, is related to the normal gradient of acoustic pressure:
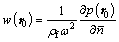 (21)
(21)
Substituting Eqs. (18-21) and (13c) into Eq. (15), and considering the orthogonality of sine and cosine integrals, a modified Kirchhoff- Helmholtz integral equation is yielded:
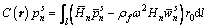 (22a)
(22a)
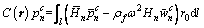 (22b)
(22b)
The acoustic boundary l should be discretized first when establishing coupling matrices of the shell-fluid interaction, to ensure that the segments of acoustic boundary match shell segments. The sound pressure on each shell segment is expanded as:
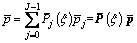 (23)
(23)
where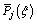 is the jth order Chebyshev orthogonal polynomials of the first kind;
is the jth order Chebyshev orthogonal polynomials of the first kind;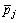 is the generalized pressure. Substituting Eqs. (23) and (13c) into Eq. (22), it can be rewritten in the following compact form:
is the generalized pressure. Substituting Eqs. (23) and (13c) into Eq. (22), it can be rewritten in the following compact form:
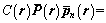
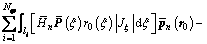
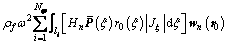 (24)
(24)
in which |Jξ| is the Jacobian of the coordinate transformation. For achieving a practical solution, the boundary integral equations in Eq. (24) are explicitly enforced at a set of collocation points ri on each shell segment as shown in Figure 2. In the local coordinate, the roots ξk are given as:
 k=1, 2, …, J (25)
k=1, 2, …, J (25)
In Eq. (25), J=1 corresponds to conventional constant boundary elements, for the pressure variable on each shell segment is assumed to be constant and the collocation points are at the center of each segment (i.e., ξ1=0). While J>1 corresponds to discontinuous boundary elements, since the collocation points located at the zeros of Chebyshev orthogonal polynomials are physically placed inside of each shell segment. The pointwise calculation of Eq. (24) for each the collocation point ri results in a set of Nφ×J linear algebraic equations for each circumferential wave mode. Considering circumferential wave modes n=0, 1, …,  Eq. (24) can be reformulated into a matrix form:
Eq. (24) can be reformulated into a matrix form:
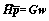 (26)
(26)
where 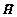 and G are the assembled coefficient matrices resulting from all circumferential wave modes,
and G are the assembled coefficient matrices resulting from all circumferential wave modes, 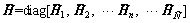 and
and 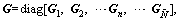 in which
in which  and Gn are assembled matrices of all shell segments for circumferential wave n, written by:
and Gn are assembled matrices of all shell segments for circumferential wave n, written by: 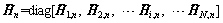 and
and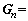
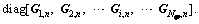
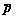 and w are the vectors containing the generalized pressure variables and the normal displacement components, which are expressed as:
and w are the vectors containing the generalized pressure variables and the normal displacement components, which are expressed as: and
and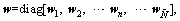 noting that
noting that and wn are assembled vectors of all shell segments for circumferential wave n. The detailed expressions of coefficient matrices
and wn are assembled vectors of all shell segments for circumferential wave n. The detailed expressions of coefficient matrices 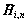 and Gi,n for the ith segment corresponding to circumferential wave n are:
and Gi,n for the ith segment corresponding to circumferential wave n are:
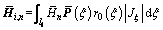 ;
;
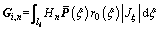 (27)
(27)
In order to eliminate the non-uniqueness of Eq. (26), Eq. (24) with collocation points outside of fluid is acted as a constraint based on the CHIEF method [27]. That is, when the collocation points ri are put exterior of the fluid, C(r) is equal to zero, and Eq. (24) becomes:
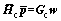 (28)
(28)
where
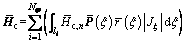 (29a)
(29a)
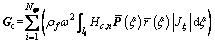 (29b)
(29b)
Through Eqs. (26) and (28), an over- determined system of equations is obtained and it can be solved by a least-squares procedure. The generalized pressure vector can be obtained:
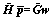 (30)
(30)
where
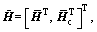
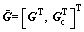 (31)
(31)
For an elliptical shell immersed in air, its vibration and sound radiation can be solved independently. Because the density of the fluid is much lower than the structural material, which indicates that the effect of the radiation loading exerted by the fluid on the structural response is negligible, so the structure-acoustic interaction analysis of elliptical shell is a loosely coupled scheme. Then, the uncoupled acoustic problem of the pressure field generated by the specified displacement/velocity distribution on the fluid-shell interface can be solved independently.
According to the concept of loosely coupled method, the structural displacement vector w can be obtained immediately, and then the generalized pressure vector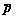 on the acoustic boundary is computed accordingly by Eq.(30); furthermore, the pressure at any position in the fluid can be determined from Eqs. (24), (23) and (18a).
on the acoustic boundary is computed accordingly by Eq.(30); furthermore, the pressure at any position in the fluid can be determined from Eqs. (24), (23) and (18a).
3 Numerical results and discussion
The present approach is general and applicable to the vibro-acoustic problem of smooth composite laminated elliptical shells. To validate its accuracy and utility, numerical results for composite laminated elliptical shells are presented. The acoustic results are expressed by sound pressure level (SPL) and sound power level (SWL):
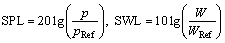 (32)
(32)
where pref is a reference sound pressure, which is defined as pref=2×10-5. The reference sound power for air is taken as Wref=1×10-12.
The first example studies the convergence of the results of the calculation with the number of segments. Table 1 lists the first ten natural frequency against the shell segment number Nφ for a cross-ply 0°/90°/0° laminated elliptical shell with C-C (clamped-clamped) boundary conditions, where M and J are selected initially as M=2 and J=2 to study the number of segments on the convergence of the natural frequencies. The geometric and material data of the shell are given as: a=1 m, b=1 m, h=0.1 m, Rs=0 m, φ0=π/12, φ1=5π/6, E2=10 GPa, E1=150 GPa, G12=G13=5 GPa, G23=6 GPa, μ12=0.25, ρ=1450 kg/m3. It is observed from Table 1 that the calculated frequencies of the present method exhibit rapid convergence trend with an increase in the number of the shell segments. In the following example, if there is no special description, the number of segments is set to Nφ=4.
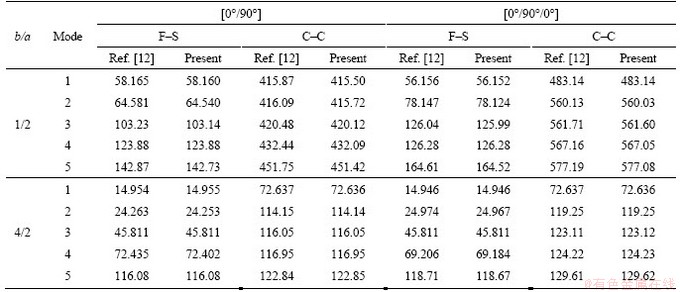
Table 2 shows the frequency parameter of a cross-ply laminated elliptical shell subjected to F-S and C-C boundary conditions. The symbol F-S identifies the elliptical shell having free boundary conditions and simply-support boundary conditions at top and bottom position boundary of the shell, respectively. The geometric data of the shell are given as: a=2 m, b=1 m and 4 m, h=0.1 m, Rs=1 m, φ0=π/6, φ1=5π/6. Material parameters are consistent with Table 1. The numerical results reported by JIN et al [12] based on a FSDT and Ritz method are also given in Table 2 for comparison. As observed from Table 2, the frequency parameters obtained by the present method are in close agreement with the contrast results.
Table 1 Frequencies against number of shell segments Nφ for a cross-ply [0°/90°/0°] laminated elliptical shell (boundary conditions: C-C)
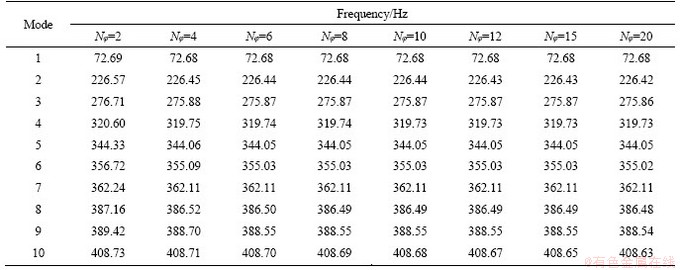
Table 2 Comparison of first five frequencies (Hz) for laminated elliptical shell with various F-S and C-C boundary conditions (a=2 m, h=0.1 m, φ0=π/6, φ1=5π/6, Rs=1 m)
The correctness of the overall stiffness matrix and the mass matrix (Eq. (14)) of the laminated elliptical shell has been preliminarily verified above, but the focus of this paper is on the acoustic results, so we will further discuss the acoustic results of the laminated elliptical shell. Figures 3 and 4 show the influence curve of the expansion terms of displacement variable function and sound pressure variable function on the convergence of acoustic results. In these two examples, the boundary conditions are defined as SS-SS and C-C respectively. Geometric constants and materials are the same as those in Table 1. The position of point load acting on elliptical shell is defined as follows:(φ, θ)=(1,0). The load direction is the normal direction of the vertical structure surface. The observation points Q of sound field is defined as (RQ,θ,z)=(10 m,0,0). The number of expansion terms of the displacement variable function is taken as 4 groups of values, which are M=2, 4, 6, 8, respectively. Similarly, the number of expansion terms of sound pressure variable function is J=1, 2, 3 and 4, respectively. It can be seen from Figures 3 and 4 that with the increase of the truncation value of the displacement variable function and sound pressure variable function, the acoustic calculation result converges rapidly. When the number of expansion terms of the sound pressure variable exceeds 2 and the number of expansion terms of the displacement variable exceeds 4, the calculation result is almost unchanged at this time. It can be considered that it has completely converged and the calculation result is reliable. Therefore, for all the later calculation examples, the cutoff value of the displacement variable function and sound pressure variable function of the laminated elliptical shell is set to M=8 and J=3.
Figure 5 shows the grouped modal contributions to the sound power level (SWL) of laminated elliptical shell immersed in air. The geometric and material parameters and boundary conditions are the same as Figure 3. It can be seen from Figure 5 that the contribution of different circumferential modes to the sound results are different. The results show that the higher-order circumferential modes (n>4) do not contribute to the radiated sound results in the frequency range considered.
In order to further investigate the circumferential radiation sound pressure of the laminated elliptical shell, sound pressure contours and circumferential directivity curve of the elliptical shell surface corresponding to the peaks in Figure 5 are given in Figures 6 and 7. Figure 6 shows the sound pressure contours of surface and directivity plots for the laminated elliptical shell with C-C boundary conditions, and Figure 7 shows the sound pressure contours of surface and directivity plots for the laminated elliptical shell with SS-SS boundary conditions. In the circumferential directivity curve of sound radiation, three kinds of circumferential distances are taken into account, i.e., RQ=10 m, RQ=20 m and RQ=30 m. Through the analysis of Figures 6 and 7, we can draw the following conclusions: firstly, the acoustic peak response points excited under different wave numbers are different, for example, point B in Figure 5(a) is determined by (n, m)=(2, 1); Secondly, at each peak point of acoustic response, it is usually the resonant response position of the structure; Lastly, the acoustic contribution at the peak point of acoustic response is mainly dominated by the resonant mode, while the contributions of other modes can be ignored.
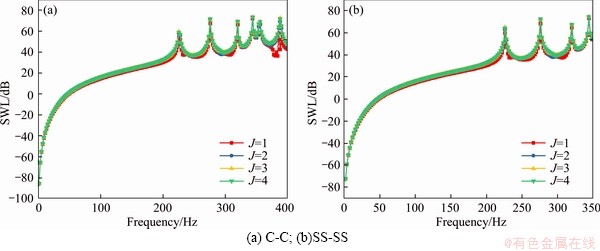
Figure 3 Comparison of radiated sound results of laminated elliptical shell with different number of expansion terms J:
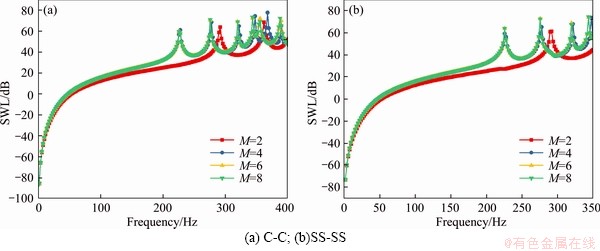
Figure 4 Comparison of radiated sound results of laminated elliptical shell with different number of expansion terms M:
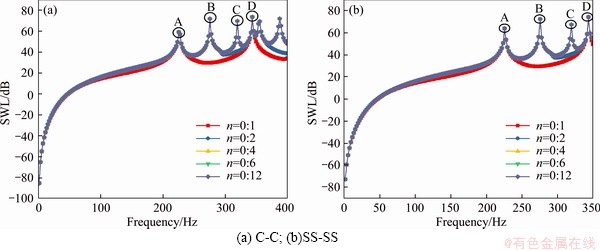
Figure 5 Sound power level of laminated elliptical shell with different circumferential modes:(A, B, C and D represent the first four resonance peaks of the sound power level)
Next, the effects of structural and material parameters on the results of structural acoustics will be further studied. Figure 8 shows the variation of the acoustic results of the laminated elliptical shell with the thickness h. The variation of the acoustic results of the laminated elliptical shell with the angle φ1 is presented in Figure 9. The material parameters are consistent with those in Table 1. It is shown that the geometric parameters in the figure are changed, and the remaining parameters are consistent with those in Table 1. Through Figures 8 and 9, it can be found that as the thickness h increases or the angle φ1 decreases, the frequency of the acoustic peak point moves to the high frequency direction, but the overall acoustic law does not change.
Finally, we further study the variation of material parameters on acoustic response for laminated elliptical shell with C-C boundary conditions. Figure 10 shows the change rule of the fiber angle θ change to the acoustic response of laminated elliptical shell. In this case, two fiber schemes, [0o/θ] and [0o/θ/0o] are considered. The geometric constants are consistent with those in Table 1. It is obvious from Figure 10 that the fiber angle has an important influence on the acoustic response of the laminated elliptical shell. Similarly, Figure 11 shows the variation of acoustic response of laminated elliptical shell with the number of fiber layers. It can be found from this figure that the peak frequency of acoustic response moves to the high frequency direction with the increase of the number of fiber layers, but when the number of layers exceeds 8, the acoustic response curve remains almost unchanged, which means that the stiffness change of the laminated elliptical shell is not very sensitive at this time.
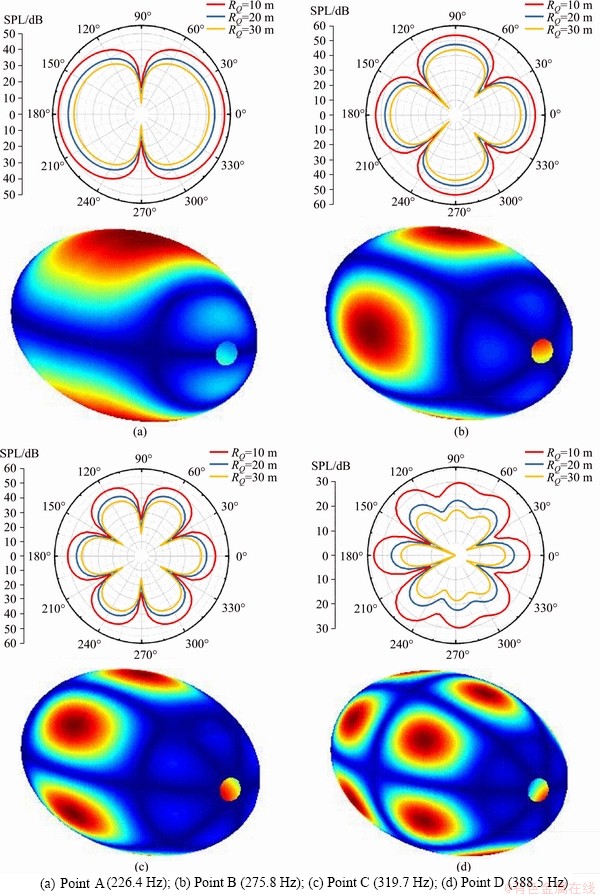
Figure 6 Sound pressure contours of surface and directivity plots for laminated elliptical shell with C-C:
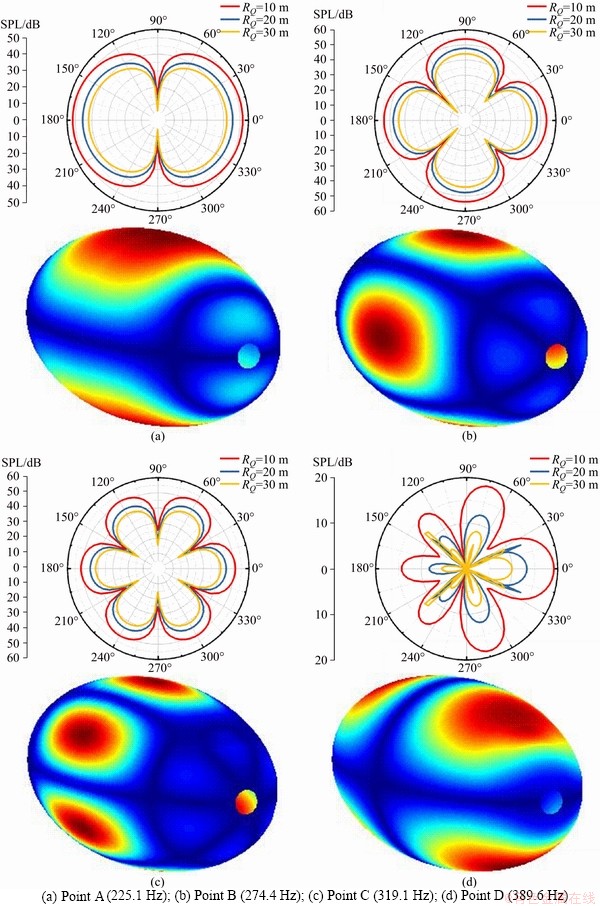
Figure 7 Sound pressure contours of surface and directivity plots for laminated elliptical shell with SS-SS:
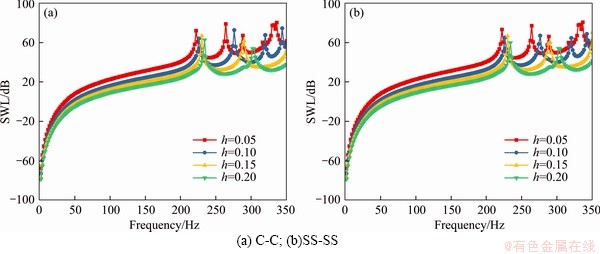
Figure 8 Sound power level of laminated elliptical shell with different thicknesses:
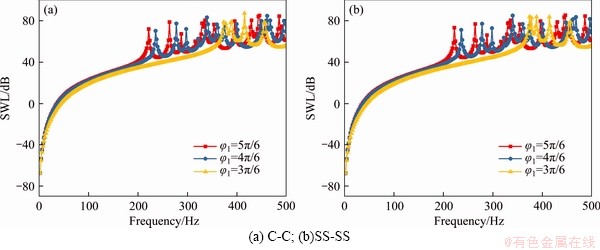
Figure 9 Sound power level of laminated elliptical shell with different angles φ1:
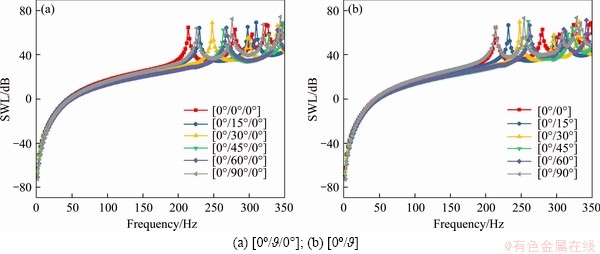
Figure 10 Sound power level of laminated elliptical shell with different fiber angles θ:
4 Conclusions
A semi-analytical method for sound radiation problems of laminated elliptical shell immersed in air is presented. Based on the first-order shear deformation shell theory, the structure model of laminated elliptical shells is established by using the variational principle and the multi-segment partitioning method. Then, a 1D Helmholtz integral formulation and CHIEF interior points are employed to set up the external acoustic field of shell. The variables including displacement and sound pressure are expanded by Fourier series and Chebyshev orthogonal polynomials. Due to the introduction of the Fourier series, the individual modal contribution to the total radiated sound of laminated elliptical shells can be analyzed directly. By comparison with the numerical results, the present solutions are validated. On this basis, some core research on acoustic response parameterization is carried out, which proves that the method presented in this paper can be used to quickly carry out the early stage evaluation of shell noise characteristics.
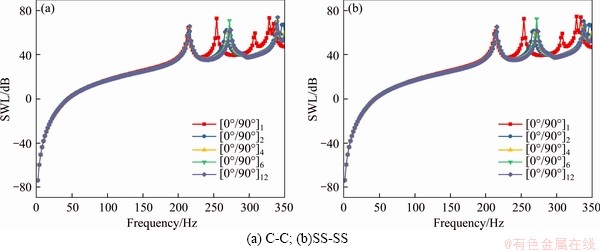
Figure 11 Sound power level of laminated elliptical shell with different fiber layer number:
Contributors
GUAN Xian-lei is responsible for writing original draft, reviewing, editing and formal analysis; ZHONG Rui is in charge of software, data and curation; QIN Bin takes part in the writing (reviewing and editing) and methodology; WANG Qing-shan plays the role of validation and writing (reviewing and editing) and SHUAI Ci-jun participates in the writing (reviewing and editing).
Conflict of interest
The authors declare that they have no conflicts of interests.
References
[1] TORNABENE F, VIOLA E, FANTUZZI N. General higher-order equivalent single layer theory for free vibrations of doubly-curved laminated composite shells and panels [J]. Composite Structures, 2013, 104: 94-117. DOI: 10.1016/ j.compstruct.2013.04.009.
[2] TORNABENE F, VIOLA E. Static analysis of functionally graded doubly-curved shells and panels of revolution [J]. Meccanica (Milan), 2012, 48(4): 901-930. DOI: 10.1007/ s11012-012-9643-1.
[3] TORNABENE F, FANTUZZI N, BACCIOCCHI M, VIOLA, E. Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells [J]. Composites Part B: Engineering, 2016, 89: 187-218. DOI: 10.1016/ j.compositesb.2015.11.016.
[4] TORNABENE F, FANTUZZI N, BACCIOCCHI M. Higher- order structural theories for the static analysis of doubly-curved laminated composite panels reinforced by curvilinear fibers [J]. Thin-Walled Structures, 2016, 102: 222-245. DOI: 10.1016/j.tws.2016.01.029.
[5] TORNABENE F, FANTUZZI N, BACCIOCCHI M. Free vibrations of free-form doubly-curved shells made of functionally graded materials using higher-order equivalent single layer theories [J]. Composites Part B: Engineering, 2014, 67: 490-509. DOI: 10.1016/j.compositesb.2014.08. 012.
[6] TORNABENE F. On the critical speed evaluation of arbitrarily oriented rotating doubly-curved shells made of functionally graded materials [J]. Thin-Walled Structures, 2019, 140: 85-98. DOI: 10.1016/j.tws.2019.03.018.
[7] WANG Qing-shan, CHOE Kwang-nam, SHI Dong-yan, SIN Ki-nam. Vibration analysis of the coupled doubly-curved revolution shell structures by using Jacobi-Ritz method [J]. International Journal of Mechanical Sciences, 2018, 135: 517-531. DOI: 10.1016/j.ijmecsci.2017.12.002.
[8] CHOE Kwang-nam, TANG Jin-yuan, SHUAI Ci-jun, WANG Ai-lun, WANG Qing-shan. Free vibration analysis of coupled functionally graded (FG) doubly-curved revolution shell structures with general boundary conditions [J]. Composite Structures, 2018, 194: 413-432. DOI: 10.1016/ j.compstruct.2018.04.035.
[9] LI Hai-chao, PANG Fu-zhen, MIAO Xu-hong, DU Yuan, TIAN Hong-ye. A semi-analytical method for vibration analysis of stepped doubly-curved shells of revolution with arbitrary boundary conditions [J]. Thin-Walled Structures, 2018, 129: 125-144. DOI: 10.1016/j.tws.2018.03.026.
[10] PANG Fu-zhen, LI Hai-chao, WANG Xue-ren, MIAO Xu-hong, LI Shuo. A semi analytical method for the free vibration of doubly-curved shells of revolution [J]. Computers & Mathematics with Applications, 2018, 75(9): 3249-3268. DOI: 10.1016/j.camwa.2018.01.045.
[11] PANG Fu-zhen, LI Hai-chao, JING Feng-mei, DU Yuan. Application of first-order shear deformation theory on vibration analysis of stepped functionally graded paraboloidal shell with general edge constraints [J]. Materials, 2018, 12(1): 69. DOI: 10.3390/ma12010069.
[12] YE Tian-gui, JIN Guo-yong, ZHANG Yan-tao. Vibrations of composite laminated doubly-curved shells of revolution with elastic restraints including shear deformation, rotary inertia and initial curvature [J]. Composite Structures, 2015, 133: 202-225. DOI: 10.1016/j.compstruct.2015.07.051.
[13] JIN Guo-yong, YE Tian-gui, WANG Xue-ren, MIAO Xu-hong. A unified solution for the vibration analysis of FGM doubly-curved shells of revolution with arbitrary boundary conditions [J]. Composites Part B: Engineering, 2016, 89: 230-252. DOI: 10.1016/j.compositesb.2015. 11.015.
[14] TALEBITOOTI R, ANBARDAN V S. Haar wavelet discretization approach for frequency analysis of the functionally graded generally doubly-curved shells of revolution [J]. Applied Mathematical Modelling, 2019, 67: 645-675. DOI: 10.1016/j.apm.2018.11.044.
[15] XIE Kun, CHEN Mei-xia, DONG Wan-jing, LI Wen-cheng. A unified semi-analytical method for vibration analysis of shells of revolution stiffened by rings with T cross-section [J]. Thin-Walled Structures, 2019, 139: 412-431. DOI: 10.1016/j.tws.2019.02.018.
[16] ZHEN Ni, ZHOU Kai, HUANG Xiu-chang, HUA Hong- xing. Free vibration of stiffened laminated shells of revolution with a free-form meridian and general boundary conditions [J]. International Journal of Mechanical Sciences, 2019, 157-158: 561-573. DOI: 10.1016/j.ijmecsci.2019.03. 040.
[17] BEROT F, PESEUX B. Vibro-acoustic behavior of submerged cylindrical shells: analytical formulation and numerical model [J]. Journal of Fluids and Structures, 1998, 12(8): 959-1003. DOI: 10.1006/jfls.1998.0179.
[18] CARESTA M, KESSISSOGLOU N J. Low frequency structural and acoustic responses of a submarine hull under eccentric axial excitation from the propulsion system [J]. Acoustics Australia, 2008, 36(2): 47-52. DOI: 10.1016/ j.jsv.2008.01.058.
[19] CARESTA M, KESSISSOGLOU N J. Acoustic signature of a submarine hull under harmonic excitation [J]. Applied Acoustics, 2010, 71(1): 17-31. DOI: 10.1016/j.apacoust. 2009.07.008.
[20] CHEN Lu-yun, LIANG Xiao-feng YI Hong. Vibro-acoustic characteristics of cylindrical shells with complex acoustic boundary conditions [J]. Ocean Engineering, 2016, 126: 12-21. DOI: 10.1016/j.oceaneng.2016.08.028.
[21] GUO Y P. Acoustic radiation from cylindrical shells due to internal forcing [J]. The Journal of the Acoustical Society of America, 1996, 99(3): 1495-1505. DOI: 10.1121/1.414728.
[22] ZOU Ming-song, LIU Shu-xiao, QI Li-bo. An analytical formulation for the underwater acoustic radiation of a cylindrical shell with an internal flexural floor based on the reciprocity theorem [J]. Applied Acoustics, 2019, 154: 18-27. DOI: 10.1016/j.apacoust.2019.04.017.
[23] LIU Shu-xiao, ZOU Ming-song, JIANG Ling-wen, ZHAO Xiao-yu. Vibratory response and acoustic radiation of a finite cylindrical shell partially covered with circumferential compliant layers [J]. Applied Acoustics, 2018, 141: 188-197. DOI: 10.1016/j.apacoust.2018.07.012.
[24] WANG Xian-zhong, CHEN Di, XIONG Ye-ping, JIANG Quan-zhou, ZUO Ying-ying. Experiment and modeling of vibro-acoustic response of a stiffened submerged cylindrical shell with force and acoustic excitation [J]. Results in Physics, 2018, 11: 315-324. DOI: 10.1016/j.rinp.2018. 09.017.
[25] CHOE Kwang-nam, WANG Qing-shan, TANG Jin-yuan, SHUAI Ci-jun. Vibration analysis for coupled composite laminated axis-symmetric doubly-curved revolution shell structures by unified Jacobi-Ritz method [J]. Composite Structures, 2018, 194: 136-157. DOI: 10.1016/ j.compstruct.2018.03.095.
[26] MARBURG S, NOLTE B. Computational acoustics of noise propagation in fluids-finite and boundary element methods [M]. Verlag Berlin Heidelberg: Springer, 2008. ISBN: 9783642096082.
[27] SCHENCK H A. Improved integral formulation for acoustic radiation problems [J]. The Journal of the Acoustical Society of America, 1968, 44(1): 41-58. DOI: 10.1121/1.1911085.
(Edited by YANG Hua)
中文导读
一种对空气中复合材料层合椭圆壳声振分析的统一预测方法
摘要:提出了一种半解析法对空气中的复合材料层合椭圆壳进行振动声分析。采用变分法和分段技术建立动力学模型。采用基尔霍夫-亥姆霍兹积分公式计算了外部流场的声辐射。用傅立叶级数和切比雪夫正交多项式组合展开了包含位移和声压的变量。引入配置点构造声积分方程代数系统,这些点分布在切比雪夫多项式的根上,并用组合亥姆霍兹积分消除系统的非唯一解。给出了复合材料层合椭圆壳声辐射问题的数值算例,并给出了周向模态对复合材料层合椭圆壳声学结果的影响。研究了几何参数和材料参数对复合材料层合椭圆壳声辐射的影响。
关键词:复合材料层合椭圆壳;半解析方法;振动;声辐射
Foundation item: Project(51705537) supported by the National Natural Science Foundation of China; Project(2018JJ3661) supported by the Natural Science Foundation of Hunan Province of China; Project(ZZYJKT2018-11) supported by State Key Laboratory of High Performance Complex Manufacturing, China
Received date: 2020-10-14; Accepted date: 2020-12-11
Corresponding author: QIN Bin, PhD, Assistant Professor; Tel: +86-13923859269; E-mail: qinbin@csu.edu.cn; ORCID: https://orcid. org/0000-0003-1796-0174

