文章编号: 1004-0609(2005)05-0688-06

微观压痕法测量Sn-Ag-Cu系无铅钎料的力学性能

王凤江¹, 钱乙余¹, 马 鑫²

(1. 哈尔滨工业大学 现代焊接生产技术国家重点实验室, 哈尔滨 150001;

2. 深圳市亿铖达工业有限公司, 深圳 518101)

摘 要: Sn-Ag-Cu系合金是最有可能替代Sn-Pb钎料的无铅钎料。 介绍了一种测量其力学性能的新方法, 即通过微压痕仪精确测量不同加载速率下压子的压入深度h与加载载荷F的关系来确定钎料的弹性模量E和蠕变速率敏感指数m。 结果表明: 加载速率对钎料蠕变压痕F-h曲线和压入深度有着重要的影响; Oliver-Pharr方法确定的钎料弹性模量取决于卸载过程而与加载速率无关。 基于压痕做功概念定义了压痕蠕变硬度和蠕变应变速率, 从而给出钎料的蠕变速率敏感指数。 Sn-3.5Ag-0.75Cu与Sn-3.0Ag-0.5Cu钎料蠕变压痕测试表明合金成分影响Sn-Ag-Cu系无铅钎料的力学性能。

关键词: 无铅钎料; 微压痕; 弹性模量; 蠕变速率敏感指数; Sn-Ag-Cu系 中图分类号: TG146.1

文献标识码: A

Measurement of mechanical properties of Sn-Ag-Cu series lead-free solder alloy by using micro-indentation

WANG Feng-jiang¹, QIAN Yi-yu¹, MA Xin²

(1. State Key Laboratory of Advanced Welding Production Technology,

Harbin Institute of Technology, Harbin 150001, China;

2. Yik Shing Tat Industrial Co., Ltd., Shenzhen 518101, China)

Abstract: Sn-Ag-Cu series alloy is considered as the lead-free alternative to lead-tin alloys. A new method was introduced to measure the mechanical properties, i.e. modulus of elasticity and creep strain rate sensitivity by using depth-sensing micro-indentation with the influence of loading rates on load—displacement (F-h) relationship. The resulting indentation F-h curves are loading-rate-dependent and have varying creep penetration depths during the same hold time. The derived modulus of elasticity values with Oliver-Pharr method from unloading curves are loading rate-independent. The creep strain rate sensitivity can be determined from the relationship between the creep hardness and creep strain rate by the definition of “work of indentation”. Also, micro-indentation tests on two Sn-3.5Ag-0.75Cu and Sn-3.0Ag-0.5Cu lead-free solder alloys show a slight influence of alloy composition on mechanical properties for Sn-Ag-Cu series solder.

Key words: lead-free solder; micro-indentation; modulus of elasticity; creep strain rate sensitivity; Sn-Ag-Cu series

SnPb钎料(特别是63Sn37Pb), 因具有低成本、 优良的力学性能和焊接性能, 成为目前电子封装与组装最主要的钎焊材料。 但是, 由于Pb对人体及环境的危害, 欧盟已明确2006年7月1日以后在电子工业中禁止Pb的使用^[1]。 因此, 为寻求63Sn37Pb共晶钎料的替代品, 近年来国际上开发并研究了许多种无Pb钎料^[2-4], 主要集中在Sn-Ag, Sn-Cu, Sn-Bi, Sn-Zn等二元或三元的Sn基钎料成分内。 很显然, 研究无Pb钎料的目的不只是简单地提供一种替代品, 还需要保证无铅钎料的力学性能、 焊接性能及其焊点的可靠性能够与传统63Sn37Pb钎料相比。 就钎料的机械性能而言, 一般采用标准拉伸和蠕变测试, 对于许多种类的无铅钎料的测试将相当费时又费钱。 因此, 希望能够给出一种简便的方法来测量无铅钎料的力学性能。

微压痕测试为解决上述问题提供了可能。 作为一种简单、 高效的评价材料力学性能的手段, 压痕实验及其应用已有近百年的历史^[5]。 通过压痕实验测量硬度和压入深度的加卸载关系, 获得材料的弹性模量、 屈服应力及幂硬化指数等^[6]。 近年来, 随着实验技术的发展和实验测量精度的提高, 人们可以在微米和纳米层次进行精细的压痕实验研究(即微压痕和纳米压痕)以获得重要的材料性能指标。 因此, 压痕实验为研究无铅钎料的力学性能提供了一种有效的测试手段。

同时, 在进行钎料焊点的可靠性评价中, 钎料的蠕变特征是导致焊点内部产生裂纹和最终失效的根本原因^[7], 因此, 无铅钎料的基本力学性能包括弹性和粘塑性(蠕变)两部分, 对无铅钎料的压痕测试应包括压痕蠕变过程。 微压痕测试过程中所得到的基本数据为载荷-位移(F-h)曲线, 由于初始卸载曲线属于弹性卸载, Oliver-Pharr方法通过分析卸载曲线的初始部分确定材料的弹性模量, 并得到了广泛的验证^{[8, 9]}; 材料的压痕蠕变实验及其F-h曲线分析则还没有相应的标准, 目前压痕蠕变实验方法主要有恒载荷法^[10]、 恒加载速率法^[11]、 恒加载速率/载荷法^[12], 并且通过F-h曲线分析得到材料的蠕变性能参数也没有合适的方法。 由于钎料蠕变性能的应变速率相关性, 本文作者在钎料压痕过程中采用不同的加载速率到固定载荷, 然后采用恒载荷法进行压痕蠕变分析, 即恒加载速率-恒载荷相结合, 分析加载速率对压痕蠕变的影响, 并基于压痕蠕变做功的概念给出无铅钎料的蠕变性能参数。

1 实验

1.1 测试材料

实验选用两种不同成分的无铅钎料: Sn-3.5Ag-0.75Cu及Sn-3.0Ag-0.5Cu。 Sn-Ag-Cu无铅钎料系列由于有着合适的熔点(217~221℃)、 良好的可焊性能、 优异的抗蠕变性能而最有可能成为替代传统63Sn37Pb钎料的标准无铅钎料^[13], 但是, 目前对Sn-Ag-Cu系无铅钎料共晶成分还存有争议^[14], 本研究所选择的两种Sn-Ag-Cu无铅钎料合金成分都在市场上得到了大程度的应用。 所选择两种Sn-Ag-Cu系无铅钎料购买于日本千住金属公司, 试样尺寸为20mm×20mm×12mm。 微压痕测试前对钎料进行机械抛光、 3%硝酸酒精腐蚀2~3s、 超声波清洗以去除表面机械变形层及氧化膜。

1.2 测试步骤

实验所用压痕仪为日本Akashi公司的MZT-4型, 加载过程为载荷控制型, 压头采用金刚石Berkovich压子。

考虑到钎料合金的典型蠕变特征, 进行了压痕蠕变测试。 测试过程中, 首先将Berkovich压子以10nm/s的速度接触样品的表面, 然后测试分成3个阶段: 以恒定的加载速率压入样品, 直到达到预定最大载荷F_m; 在最大载荷F_m下保持5s以进行蠕变; 卸载, 卸载时间为1s。

钎料合金属于非均质材料, 图1所示为Sn-3.0Ag-0.5Cu无铅钎料的低倍及高倍显微组织, 低倍条件下观察到钎料是由白色的β-Sn相基体和灰色的共晶相组成, 而共晶相在高倍显微条件下可看出是由β-Sn相和细条状的金属间化合物相交错分布的, X射线衍射表明这些金属间化合物是Cu₆Sn₅和Ag₃Sn。 由于相的颗粒大小达到微米数量级, 微压痕测试时当最大载荷采用纳米数量级时只会对钎料的单相进行压痕测试, 因此本压痕实验中采用大载荷, 最大载荷F_m为500mN, 微压痕实验证明钎料能够得到很好的均质响应, 而且其重复操作性良好。 考虑到钎料合金的蠕变应变速率相关特征, 加载速率分别为0.25, 0.5, 1, 2, 5, 10, 20, 50及100mN/s。

图1   Sn-3.0Ag-0.5Cu无铅钎料显微组织

Fig.1   Microstructures of Sn-3.0Ag-0.5Cu

lead-free solder with different magnifications

2 测量原理

无铅钎料的力学性能包括了弹性和粘塑性(蠕变), 具体关系式为

式中 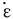为总应变速率;为弹性硬变速率; 为蠕变应变速率; E为弹性模量; n为蠕变应力敏感指数; A为材料常数; σ为应力; 为应力变化速率。

钎料微压痕实验所产生的结果为载荷—位移曲线, 这条曲线提供了丰富的信息用于材料力学性能的导出, 但首先需要给出曲线的物理分析手段。

2.1 弹性接触压痕分析—弹性模量(E)

图2所示为无铅钎料压痕测试所得到的典型载荷—位移曲线, 分为3部分: 加载过程、 最大载荷保持过程及卸载过程。

Oliver-Pharr法是比较普遍接受的确定弹性模量的一种方式, 即假设了卸载曲线的初始阶段为线性的。 通过定义弹性接触刚度S(如图2所示)为卸载初始阶段卸载曲线的斜率, 给出了弹性模量的计算^{[8, 9]}:

式中 h_c为接触深度; h_max为最大压入深度; ε为取决于压子形状的常数(对Berkovich压子, ε=0.72); β为压子非对称的修正系数(对Berkovich压子, β=1.034); A为接触面积; E_eff定义为有效弹性模量; E, ν分别为实验材料的弹性模量和泊松比(本文中钎料的值取为0.3); E_i, ν_i分别为压子材料的弹性模量和泊松比。 结合方程(2)~(4), 可以确定出实验材料的弹性模量。

图2   钎料合金的典型微压痕曲线

Fig.2   Typical indentation load—depth

curve for rate-dependent creep solder alloy

2.2 粘塑性(蠕变)压痕分析—蠕变速率敏感指数(m=1/n)

图3所示为Sn-3.5Ag-0.75Cu无铅钎料不同加载速率下的蠕变压痕曲线。 随着加载速率的增加, 压痕蠕变所产生的位移也明显增加, 见图3中不同加载速率条件下最大载荷保持5s时所产生的曲线。 钎料的蠕变应变速率敏感指数可从载荷—位移曲线的恒载荷段确定。 本研究基于压痕做功这一特征去构建钎料合金的应力—应变关系, 从而得到指数m, 图2中给出了压痕蠕变做功示意图。

图3   Sn-3.5Ag-0.75Cu无铅钎料微压痕

加载速率对压痕—位移曲线的影响

Fig.3   Load—displacement indentation curves with different loading rates for Sn-3.5Ag-0.75Cu solder alloy

根据Stilwell和Tabor的压痕做功概念^[15], 即压痕实验时加载载荷所做的功反映了材料受变体积(压子一定时即压入深度)的变化^{[15, 16]}。 由于硬度反映了材料的应力特征, 本研究就采取了压痕过程最直接的硬度这一参数。 因而, 最大载荷处保持一段时间所产生的蠕变过程中蠕变硬度可描述为

W_cr和ΔV_cr可分别表示为(如图4所示):

式中 g为Berkovich压子的形状因子(取24.56); H_cr为蠕变硬度; W_cr为蠕变做功; ΔV_cr为蠕变变形体积; h_ml为加载到最大载荷处位移; h_mu为初始卸载点位移。

图4   压痕测试过程中蠕变做功示意图

Fig.4   Schematic of creep deformed

volume during hold time in indentation test

同时, 对于压痕蠕变应变, 如图4所描述硬度测试时存在一半球形Johnson弹塑性边界^[17], 即整个测试过程中材料所发生的塑性变形都处于半球之内, 半球之外则为纯弹性。 塑性区半径c可表示为

式中 σ_y为屈服强度(σ_y=H/3.0^[18])。 在给定加载速率及F_m情况下, H_cr一定, 所产生的塑性半球也就固定。 从而可以定义蠕变过程中的应变:

式中 V_p为塑性变形体积; Δt为蠕变时间, 本实验中钎料压痕蠕变时间均为5s。

根据上述分析, 通过F-h曲线可以描述不同加载速率条件下的lnH和的线性关系, 从而得到钎料合金的应力敏感指数n, 钎料的蠕变应变速率敏感指数m=1/n。

3 结果与分析

从图3所给出的不同加载速率下Sn-3.5Ag-0.75Cu钎料蠕变压痕F-h曲线, 结合图2可以看出, 曲线中包括3个重要的位移点: h_ml, h_mu, h_r(剩余位移), 同时还有蠕变深度Δh(=h_mu-h_ml)。 图5所示为Sn-3.5Ag-0.75Cu和Sn-3.0Ag-0.5Cu无铅钎料的Δh, h_ml和h_mu与加载速率的关系。 可以发现, 它们都遵循共同的规律, 即在恒定的加载速率条件下随着压入载荷的增加, 压入深度呈非线性增加, 当达到最大载荷F_m保持一段时间时, 由于蠕变的作用压入深度继续增加, 且增加的程度取决于加载速率。 另一方面, 在相同载荷条件下, 压痕实验时加载过程中所产生的压痕深度(h_ml)随加载速率的增加而降低, 相反最大载荷处所产生的蠕变深度(Δh)则随加载速率的增加而增加。

图5   Sn-Ag-Cu系列钎料蠕变压痕加载速率对压入深度的影响

Fig.5   Effects of loading rate on penetration

depth for Sn-Ag-Cu lead-free solder alloys

由方程(6)和(10)可以分别计算出不同加载速率下的蠕变应变速率及蠕变硬度。 图6所示为蠕变应变速率与蠕变硬度的关系。 可以看出它们的对数值呈线性关系, 从而确定出Sn-3.5Ag-0.75Cu和Sn-3.0Ag-0.5Cu无铅钎料的蠕变应变速率敏感指数m分别为0.0860和0.1111, 其中Sn-3.5Ag-0.75Cu无铅钎料的应力敏感指数n为11.63, 接近于文献[19]中所给出的值(n=12)。 同时, 由方程(4)和(5)可以计算出不同加载速率下对应微压痕曲线的弹性模量(图6), 可以看出, 钎料的弹性模量不受压痕加载条件的影响, 而只取决于卸载曲线的初始部分, 所确定的Sn-3.5Ag-0.75Cu和Sn-3.0Ag-0.5Cu无铅钎料弹性模量分别为12.0GPa和9.3GPa。 另一方面, 测试也表明了不同成分的Sn-Ag-Cu系列无铅钎料间的力学性能还是存在着差别。 由图1中钎料的显微组织可看出, 合金元素Ag和Cu在钎料中以金属间化合物形式弥散分布于Sn基体内, 这种弥散分布的金属间化合物相能增加钎料的硬度及其抗蠕变能力, Ag和Cu元素含量的提高导致金属间化合物相含量的增加, 也就提高了钎料的弹性模量和应力敏感指数。

图6   Sn-Ag-Cu无铅钎料压痕蠕变应变速率敏感指数与弹性模量的导出

Fig.6   Derived values of creep strain rate

sensitivity and modulus of elasticity for

Sn-Ag-Cu lead-free solders alloys

4 结论

1) 微压痕仪具有很高的位移和载荷分辨率, 为考察无铅钎料的力学性能提供了一种新的手段。 用该法测量钎料的弹性和粘塑性(蠕变)性能, 不但方法简单, 对样品尺寸要求不高, 而且测量精度高。

2) Sn-Ag-Cu系无铅钎料的蠕变微压痕测试表明, 加载速率对压痕F-h曲线及其蠕变特征有显著影响。 随着加载速率的增加, 加载过程所产生的压痕深度降低; 相反, 恒载过程所产生的蠕变深度增加。

3) Oliver-Pharr方法对压痕F-h卸载曲线的分析给出了钎料的弹性模量。 Sn-3.5Ag-0.75Cu和Sn-3.0Ag-0.5Cu无铅钎料的弹性模量分别为12.0GPa和9.3GPa, 并且均与加载速率无关。

4) 基于压痕F-h恒载蠕变曲线提出压痕做功概念, 由不同加载速率下的蠕变硬度和蠕变应变速率关系给出了钎料蠕变应变速率敏感指数, Sn-3.5Ag-0.75Cu和Sn-3.0Ag-0.5Cu无铅钎料的蠕变应变速率敏感指数分别为0.0860和0.1111。

5) 对Sn-Ag-Cu系无铅钎料而言, 由于合金元素Ag和Cu是以金属间化合物相形式存在, Ag和Cu含量的变化会导致钎料力学性能发生变化。

REFERENCES

[1]Directive 2002/96/EC of the European Parliament and of the Council of 27 January 2003 on the restriction of the use of certain hazardous substances in electrical and electronic equipment[J]. Official Journal of the European Union, 2003, L37: 19-23.

[2]Glazer J. Metallurgy of low temperature Pb-free solders for electronic assembly[J]. International Materials Reviews, 1995, 40: 65-93.

[3]Abtew M, Selvaduray G. Lead-free solders in microelectronics[J]. Mater Sci Eng Reports, 2000, 27: 95-141.

[4]Suganuma K. Advances in lead-free electronics soldering[J]. Current Opinion in Solid State and Materials Science, 2001, 5: 55-64.

[5]Tabor D. Indentation hardness: Fifty years on a personal view[J]. Philo Mag A, 1996, 74(5): 1207-1212.

[6]Suresh S, Alcala J, Giannakopoulos A E. Spherical indentation of compositionally graded materials: Theory and experiments[J]. Acta Materialia, 1997, 45(4): 1307- 1321.

[7]Lau J H. Solder Joint Reliability: Theory and Application[M]. New York: Van Nostrand Reinhold, 1991. 85-93.

[8]Oliver W C, Pharr G M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments[J]. J Mater Res, 1992, 7: 1564-1583.

[9]Bolshakov A, Pharr G M. Influences of pileup on the measurement of mechanical properties by load and depth sensing indentation techniques[J]. J Mater Res, 1998, 13(4): 1049-1058.

[10]Mayo M J. Nanoindentation of nanocrystalline ZnO[J]. J Mater Res, 1992, 7(4): 973-979.

[11]Mayo M J, Nix W D. Micro-indentation study of superplasticity in Pb, Sn, and Sn-38wt% Pb[J]. Acta Metall, 1988, 36(8): 2183-2192.

[12]Lucas B N, Oliver W C. Indentation power-law creep of high-purity indium[J]. Metall Mater Trans A, 1999, 30A: 601-610.

[13]Richards B P, Levoguer C L, Hunt C P, et al. An Analysis of the Current Status of Lead-free Soldering[R]. NPL and ITRI Report, 1999.

[14]Ohnuma I. Phase equilibria and the related properties of Sn-Ag-Cu based Pb-free solder alloys[J]. J Electron Mater, 2000, 29: 1137-1144.

[15]Stilwell N A, Tabor D. Elastic recovery of conical indentations[J]. Proc Phys Soc, 1961, 78: 169-179.

[16]Tuck J R, Korsunsky A M, Bull S J, et al. On the application of the work-of-indentation approach to depth-sensing indentation experiments in coated systems[J]. Surf Coat Technol, 2001, 137: 217-224.

[17]Johnson K L. The correlation of indentation experiments[J]. J Mech Phys Solids, 1970, 18: 115-126.

[18]Tabor D. Hardness of Metals[M]. London: Oxford University Press, 1951. 38-43.

[19]Wiese S, Meusel E, Wolter K J. Microstructural dependence of constitutive properties of eutectic SnAg and SnAgCu solders[A]. 53rd ECTC[C]. 2003. 197-206.

收稿日期: 2004-11-08; 修订日期: 2005-01-17

作者简介: 王凤江(1977-), 男, 博士研究生.

通讯作者: 王凤江; 电话: 0769-6713876-181; E-mail: wangfj@hit.edu.cn

(编辑陈爱华)