DOI: 10.11817/j.issn.1672-7207.2019.05.027

橡胶颗粒沥青砂非线性蠕变模型试验研究

刘浩轩^1,2，曾国伟^1,2，白凡³，吴亮¹，郑华升¹

(1. 武汉科技大学 理学院，湖北 武汉，430065；

2. 冶金工业过程系统科学湖北省重点实验室，湖北 武汉，430081；

3. 武汉第二船舶设计研究所，湖北 武汉，430205)

摘要：为了研究橡胶颗粒沥青砂非线性蠕变回复行为，基于Schapery黏弹性模型理论，并结合改进型Swchartz黏塑性模型，提出一种改进的积分型本构模型；开展一系列橡胶颗粒沥青砂压缩蠕变试验，通过最小二乘法与改进欧拉法对实验数据进行拟合，确定模型中各参数；最后，利用模型对不同应力水平下橡胶颗粒沥青砂的蠕变回复行为进行预测。研究结果表明：该蠕变本构模型不仅能准确描述橡胶颗粒沥青砂蠕变过程中复杂的非线性黏弹塑性行为，并且可用来预测不同应力水平橡胶颗粒沥青砂蠕变特性；相比于其他模型，本文模型中参数的确定简单、方便。

关键词：橡胶颗粒沥青砂；蠕变参数；本构模型；数值拟合

中图分类号：U414              文献标志码：A         文章编号：1672-7207(2019)05-1229-06

Experimental research on nonlinear creep model of crumb rubber asphalt sand

LIU Haoxuan^1,2, ZENG Guowei^1,2, BAI Fan³, WU Liang¹, ZHENG Huasheng¹

(1. School of Science, Wuhan University of Science and Technology, Wuhan 430065, China;

2. Hubei Province Key Laboratory of Systems Science in Metallurgical Process, Wuhan 430081, China;

3. Wuhan Second Ship Design and Research Institute, Wuhan 430205, China)

Abstract: Based on Schapery viscoelastic model theory, and then combined with improved Swchartz viscoplastic model, an improved integral constitutive model was proposed to study the nonlinear creep recovery behavior of crumb rubber asphalt sand. A series of compressive creep tests were conducted on crumb rubber asphalt sand, and then the experimental data were fitted by the least squares and improved Euler method to determine the parameters in the model. Finally, the model was used to predict the creep recovery behavior of crumb rubber asphalt sand at different stress levels. The result shows that the creep constitutive model can not only accurately describe the complex nonlinear viscoelastic-plastic behavior of crumb rubber asphalt sand during the creep process, but also can be used to predict the creep characteristics of crumb rubber asphalt sand with different stress levels. Compared to other models, the parameter determination of the proposed model parameters is simple and convenient.

Key words: crumb rubber asphalt sand; creep parameters; constitutive model; numerical fitting

沥青路面是我国道路路面的主要形式，将橡胶颗粒添加到沥青混合料中，使沥青道路具有较大弹性，可达到资源重复利用和清除路表结冰的目的^[1]，因此，橡胶颗粒沥青混合料的力学特性一直是研究热点。沥青混合料的本构关系一直受到研究者们的关注^[2-5]，新模型、新方法不断呈现。国内外研究者采用变形分解的方法将黏弹性、黏塑性进行组合，其中黏弹性部分采用微分型^[6-8]模型进行描述，而黏塑性部分主要采用Uzan模型、Perzyna模型和曹树刚模型等以及时间应力相关函数进行描述^[9-10]。然而，在高温和较大应力下，沥青混合料呈现非线性特点，材料的应力应变关系不再满足线性叠加原理。因此，有必要采用Schapery模型来描述非线性黏弹性响应，再引入黏塑性项，组合为积分型本构模型，最终合理地描述沥青混合料非线性黏弹塑性行为。关于积分型本构模型试验研究，SIDES等^[11]进行了大量沥青砂单轴拉压的蠕变回复试验，通过研究不同时间不同应力作用下沥青砂的残余应变特征，将沥青砂的蠕变分为瞬时弹性、瞬时塑性、黏弹性和黏塑性4个部分，采用一系列单轴蠕变回复试验确定模型参数，使得沥青混合料的蠕变性质研究变得简单方便。BAI等^[12]采用简化的Schapery非线性黏弹性本构模型和Swchartz黏塑性本构模型分别描述沥青砂的可回复变形和不可回复变形，进行应力递增的循环蠕变试验以确定黏弹性参数，并结合单次蠕变试验确定黏塑性参数，探究理想级配沥青混合料黏弹塑性性质。橡胶颗粒沥青砂由沥青、橡胶颗粒和矿料组成，因其具有抑制路面积雪结冰和降噪、抗滑的特点而受到广泛关注^[1,13]。但有关橡胶颗粒沥青混合料蠕变模型的研究较少，有关积分型蠕变模型的研究则更少。本文作者在BAI等^[12]的研究基础上，开展橡胶颗粒沥青砂(简称为沥青砂)的单轴蠕变模型研究，将沥青砂蠕变总变形分为4个部分；采用改进的Schapery黏弹性模型和改进的黏塑性模型，引入瞬时塑性模型，根据一系列单轴压缩蠕变试验结果确定模型参数，并利用模型对不同应力条件下沥青砂的应变响应进行预测，验证模型的适用性。

1  耦合蠕变模型

1.1  应变的分解

本文将沥青砂的蠕变分解为瞬时弹性变形ε_e、瞬时塑性变形ε_p、黏弹性变形ε_ve和黏塑性变形和ε_vp这4个基本部分进行描述。沥青砂变形分解图如图1所示(其中 t为时间；t_o为卸载时刻)。

总蠕变应变ε(t)可表示为

            (1)

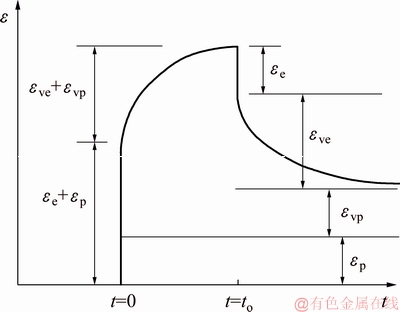
图1  沥青砂变形分解图

Fig. 1  Diagram of asphalt sand deformation decomposition

1.2  瞬时弹性和黏弹性模型

为了描述沥青砂在高温、复杂应力作用下依赖时间的非线性黏弹性响应，采用Schapery非线性黏弹性模型。将Schapery模型分解成瞬时弹性模型和黏弹性模型：

                (2)

      (3)

式中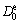：为瞬时弹性蠕变柔量；σ为应力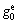；，g₂和α_σ为只与应力有关的非线性参数，α_σ为应力移位因子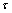；为已经历的时间；和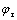为折算时间，分别反映载荷作用时间在不同应力水平下的放大和缩小效应；△D为依赖时间t的短时蠕变柔量，△D=D(t)-D₀。将D(t)设为时间的指数函数，即

D(t)=Ctⁿ                 (4)

式中：n和C为常数，可通过试验确定。

从蠕变开始到t_o时刻蠕变结束，黏弹性变形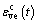可表示为

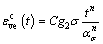             (5)

卸载后(t＞t_o)的回复阶段，黏弹性变形可表示为

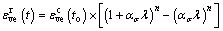    (6)

式中：。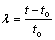

1.3  瞬时塑性和黏塑性模型

对于不可回复应变部分，本文采用瞬时塑性和黏塑性耦合模型进行描述，其中瞬时塑性项ε_p为

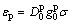                (7)

式中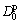：为瞬时塑性蠕变柔量，为只与应力相关的非线性参数。在加载瞬时，沥青混合料产生的瞬时塑性变形在应力不变的蠕变过程中不发生改变。

对于黏塑性模型，在单轴载荷作用下，Uzan模型^[14]可以较精准地表示沥青砂的黏塑性变形。SCHWARTZ等^[15]在此基础上提出指数形式的应力函数表达式。为了更好地描述大应力范围内沥青混合料的非线性性质，本文采用BAI等^[8]提出的改进型Schwartz黏塑性本构模型：

        (8)

式中：σ_u为单位应力；σ_m为线性应力极限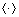；为Macaulay括号；，k，p和q为材料常数；△为用来消除零点奇异性所引入的极小量。

综合式(2)，(7)和(8)，即可得到沥青砂常应力蠕变模型方程：

               (9)

2  蠕变试验

2.1  试验材料

沥青砂^[10]是指在标准级配沥青混合料中，由沥青和粒径小于2.36 mm的细集料组成的基体部分。本文橡胶颗粒沥青砂在AC-13密级配沥青混合料基础上，去除粒径大于2.36 mm的粗集料，同时沥青外掺质量分数约为20%的橡胶粉。叶永^[16]经过实验研究确定AC-13沥青混合料的最佳油石质量比为4.6%～5.1%。

根据这一范围，本文设定沥青砂油石质量比为14.0%，最终各部分质量配比如表1所示。

试验所用沥青型号为AH-70重交通道路沥青。集料采用石灰岩最大粒径为2.36 mm；填料为石灰岩矿粉，粒径小于0.075 mm。橡胶颗粒使用粒径为0.5～0.6 mm的废胎胶粉，为了达到更好的改性效果，采用湿拌法加入到沥青中。

2.2  试件成型与试验方法

参考JTG E20—2011“公路工程沥青及沥青混合料试验规程”^[17]，采用静压法制作直径和高度均约为50 mm的圆柱体沥青砂试件。将成型的试件进行编号，测量试件的直径与高度，允许的偏差为±0.5 mm。然后测定试样空中质量、水中质量、表干密度等物理参数，以便计算试样孔隙率。为了减少平行试件性能差异对试验结果的影响，所有试验试件孔隙率控制为1.4%以下，同时剔除不满足设计指标的试件。

针对圆柱形沥青砂试件，采用配置有环境温度箱的万能材料试验机，在25 ℃下进行一系列试验，包括应力递增的蠕变回复试验、单次蠕变试验和单次蠕变回复试验等。各试验加载历史分别如表2和表3所示。各试验重复进行3次，结果取其平均值。

对于应力递增的蠕变回复试验，每个回复阶段时间足够长，可以认定此段时间内黏弹性变形完全回复。因此，作如下假设：应力递增的蠕变回复试验中的回复曲线，经过平移减去相应的残余应变，可看作不同应力下单次蠕变回复试验的回复曲线。采用应力递增的蠕变回复试验确定瞬时塑性、瞬时弹性、黏弹性模型参数，采用应力为0.3 MPa的蠕变试验确定黏塑性参数，采用其他试验进行模型的预测验证。

2.3  试验结果处理

图2所示为沥青砂在应力递增的蠕变回复试验中的应变曲线。由图2可以看出：随着应力的增加，蠕变回复后的残余变形越大，初步证明了本文黏塑性模型的合理性。

将图2中各回复阶段应变进行平移处理，即可得到不同应力作用下沥青砂在回复阶段的黏弹性应变曲线，如图3所示。图3中的应变曲线可用于确定黏弹性参数。

表1  橡胶颗粒沥青砂的配合比

Table 1  Mix proportion of crumb rubber asphalt sand

表2  应力递增的蠕变回复试验加载历史

Table 2  Loading history of creep-recovery tests under increasing stress

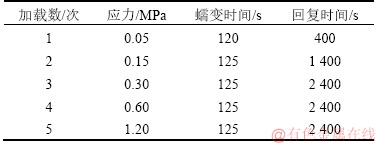
表3  单次蠕变与蠕变回复试验加载历史

Table 3  Loading history of single creep and creep-recovery tests

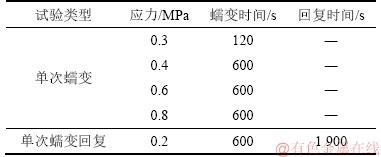
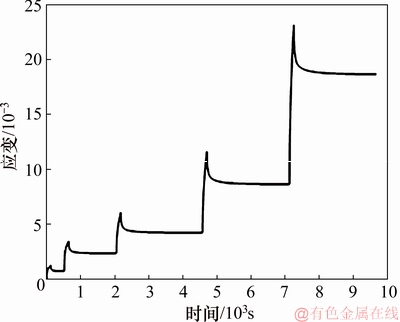
图2  沥青砂在应力递增的蠕变回复试验中的应变曲线

Fig. 2  Strain curves of asphalt sand in creep-recovery test under increasing stress

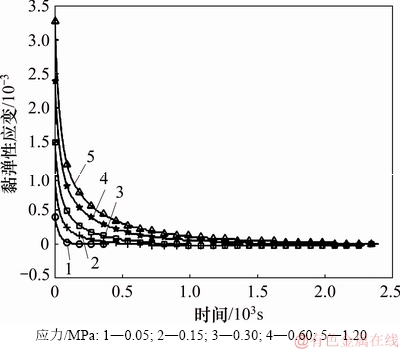
图3  沥青砂回复阶段的黏弹性应变曲线

Fig. 3  Viscoelastic strain curves of asphalt sand in recovery phase

3  模型参数确定

3.1  瞬时弹性、瞬时塑性和黏弹性参数的确定

参数文献[8]和文献[18-19]，设定0.1 MPa为沥青砂蠕变行为线性与非线性范围应力分界点，在小应力(≤0.1 MPa)作用时，式(2)中所有与应力相关的参数值为1，即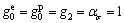。此时，瞬时弹性应变为卸载瞬时回复应变，可直接从试验数据中读取。在σ=0.05 MPa时，ε_e=2.44×10^-4，求得 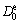=4.88×10^-3 MPa^-1。瞬时塑性应变为加载瞬时应变与卸载瞬时回复应变的差值，在σ=0.05 MPa时，ε_p=1.47×10^-4，求得 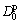=2.94×10^-3 MPa^-1。将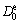和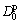代入式(3)和式(7)，可采用类似的方法，利用其他应力作用下的瞬时弹性应变和瞬时塑性应变确定应力相关的非线性参数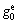和，结果见表4。

当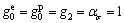时，式(5)和式(6)可简化为

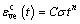              (10)

      (11)

针对图3中0.05 MPa应力对应的黏弹性应变曲线，采用Matlab对式(10)和(11)进行参数拟合^[20]，求得线性范围内黏弹性参数C=0.00 235，n=0.150 9。将C和n代入式(5)和式(6)，应力相关的非线性参数g₂和α_σ可利用其他回复曲线数据拟合确定(见表4)。

表4  应力相关参数拟合结果

Table 4  Fitting results of stress-related parameters

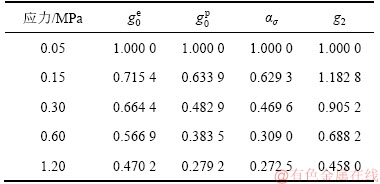
在非线性应力水平(应力大于0.1 MPa)，应力相关参数随应力变化，本文采用指数函数进行拟合得到如下函数关系：

    (12)

3.2  黏塑性参数确定

沥青砂在任意应力蠕变下的瞬时塑性应变ε_p、瞬时弹性应变ε_e和黏弹性应变ε_ve可以通过3.1节中的模型进行预测。将试验总应变减去预测应变便可得到蠕变过程中的黏塑性应变ε_vp。本文采用应力为0.3 MPa时的蠕变试验结果，利用改进欧拉法拟合式(8)中模型参数，结果如表5所示。

表5  黏塑性参数拟合结果

Table 5  Fitting results of viscoplastic parameters

图4所示为应力为0.3 MPa时沥青砂在蠕变试验中的黏塑性应变及拟合结果。由图4可以看出：BAI等^[12]提出的黏塑性模型适用于描述橡胶颗粒沥青砂黏塑性性质。

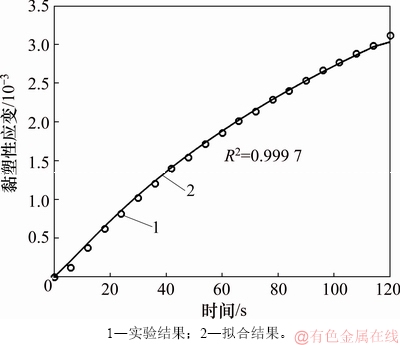
图4  应力为0.3 MPa时沥青砂在蠕变试验中的黏塑性应变及拟合结果

Fig. 4  Viscoplastic strain and fitting result of asphalt sand in creep test with stress of 0.3 MPa

4  模型预测与验证

为验证模型的合理性，分别将已确定的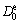和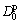以及表5中的模型参数和式(12)中预测的参数代入到式(9)中，首先进行25 ℃，不同应力作用下蠕变变形预测，并与试验结果进行对比。图5所示为0.4，0.6和0.8 MPa应力水平下试验结果与本文模型预测结果对比。从图5可以看出：本文模型可较好地预测任意应力作用下橡胶颗粒沥青砂的蠕变行为，证明了本文模型的合理性。

在0.2 MPa应力水平下对单次蠕变回复变形预测，并与试验结果对比。图6所示为应力为0.2 MPa时单次蠕变回复试验结果与本文模型预测对比图。由图6可以看出：可能由于试件随机性影响，预测结果与试验结果存在偏差，但预测曲线与试验曲线趋势一致，证明本文模型也可以预测橡胶颗粒沥青砂蠕变回复变形。

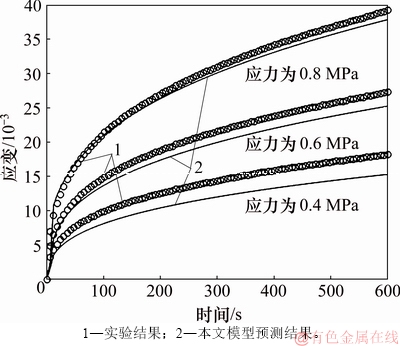
图5  沥青砂在不同应力水平蠕变试验中的应变响应

Fig. 5  Strain response of asphalt sand in creep tests with different stresses

图6  应力为0.2 MPa时沥青砂在蠕变回复试验中的应变 响应

Fig. 6  Strain response of asphalt sand in creep-recovery test with stress of 0.2 MPa

5  结论

1) 在改进型Schapery模型的基础上，引入瞬时塑性模型，并耦合黏塑性模型，提出一种新的橡胶颗粒沥青砂的积分型蠕变模型。

2) 本文模型将应变各部分分解，通过橡胶颗粒沥青砂应力递增的蠕变回复试验和单次蠕变试验即可确定所有参数，并提出部分非线性参数与应力的函数关系；与其他的模型相比，本文模型参数确定更加简单、方便。

3) 与实验结果相比，本文模型能很好地描述预测橡胶颗粒沥青砂任意应力下的蠕变行为，虽然预测蠕变回复行为则略有偏差，但预测变形与实验曲线趋势一致。

参考文献：

[1] 陈渊召, 李振霞. 橡胶颗粒沥青路面的除冰机理[J]. 中南大学学报(自然科学版), 2013, 44(5): 2073-2081.

CHEN Yuanzhao, LI Zhenxia. Deicing mechanism for crumb rubber asphalt pavement[J]. Journal of Central South University (Science and Technology), 2013, 44(5): 2073-2081.

[2] WU Qiang, WANG Chong, LANG Rui, et al. Fractional linear viscoelastic constitutive relations of anhydride-cured thermosetting rubber-like epoxy asphalt binders[J]. Construction and Building Materials, 2018, 170: 582-590.

[3] 张丽娟, 张肖宁, 陈页开. 沥青混合料变形的粘弹塑性本构模型研究[J]. 武汉理工大学学报(交通科学与工程版), 2011, 35(2): 289-292.

ZHANG Lijuan, ZHANG Xiaoning, CHEN Yekai. Viscoelasto- plastic constitutive model of deformation for asphalt mixtures[J]. Journal of Wuhan University of Technology(Transportation Science and Engineering), 2011, 35(2): 289-292.

[4] 李锐铎, 乐金朝, 冯师蓉, 等. 沥青胶砂改进分数阶导数幂函数经验蠕变本构模型[J]. 建筑材料学报, 2015, 18(2): 237-242.

LI Ruiduo, YUE Jinchao, FENG Shirong, et al. Improved fractional order derivative empirical power function model for describing the creep of asphalt mortar[J]. Journal of Building Materials, 2015, 18(2): 237-242.

[5] 宋航. 沥青混凝土力学性能试验及本构关系对比研究[D]. 宜昌: 三峡大学水利与环境学院, 2014: 60-68.

SONG Hang. Mechanical properties tests and constitutive relation comparative study of asphalt concrete[D]. Yichang: Sanxia University. College of Hydraulic and Environment Engineering, 2014: 60-68.

[6] 王芝银, 李云鹏. 岩体流变理论及其数值模拟[M]. 北京: 科学出版社, 2008: 28-31.

WANG Zhiyin, LI Yunpeng. Rock mass rheological theory and numerical simulation[M]. Beijing: Science Press, 2008: 28-31.

[7] YE Yong, YANG Xinhua, CHEN Chuanyao. Viscoelastoplastic constitutive model for creep deformation behavior of asphalt sand[J]. Journal of Central South University, 2008, 15(S1): 13-16.

[8] YE Yong, YANG Xinhua, CHEN Chuanyao. Experimental researches on viscoelastoplastic constitutive model of asphalt mastic[J]. Construction and Building Materials, 2009, 23(10): 3161-3165.

[9] LU Y, WRIGHT P J. Numerical approach of viscoelastoplastic analysis for asphalt mixtures[J]. Computers and Structures, 1998, 69(2): 139-147.

[10] 杨新华, 白凡, 叶永, 等. 沥青混合料力学[M]. 北京: 科学出版社, 2016: 15-42.

YANG Xinhua, BAI Fan, YE Yong, et al. Mechanics of asphalt mixture[M]. Beijing: Science Press, 2016: 39-42.

[11] SIDES A, UZAN J, PERL M. A comprehensive visco-elastoplastic characterization of sand-asphalt compressive and tensile cyclic loading[J]. ASTM Journal of Testing and Evaluation, 1985, 13(1): 49-59.

[12] BAI Fan, YANG Xinhua, ZENG Guowei. A stochastic viscoelastic-viscoplastic constitutive model and its application to crumb rubber modified asphalt mixtures[J]. Materials & Design, 2016, 89: 802-809.

[13] 陈渊召, 李振霞. 基于复合材料的橡胶颗粒沥青混合料弹性模量预测[J]. 中南大学学报(自然科学版), 2013, 44(6): 2609-2616.

CHEN Yuanzhao, LI Zhenxia. Elastic modulus prediction of crumb rubber asphalt mixture based on composite material[J]. Journal of Central South University (Science and Technology), 2013, 44(6): 2609-2616.

[14] UZAN J, SIDES A, PERL M. Visco-elasto-plastic model for predicting asphaltic mixture performance[J]. Transportation Research Record, 1985, 1043: 78-89.

[15] SCHWARTZ C W, GIBSON N H, SCHAPERY R A, et al. Viscoplasticity modeling of asphalt concrete behavior[C]// 15th Engineering Mechanics Division Conference. New York, United States: ASCE, 2002: 144-159.

[16] 叶永. 沥青混合料粘弹塑本构模型的实验研究[D]. 武汉: 华中科技大学土木工程与力学学院, 2009: 87-89.

YE Yong. Experimental researches on visco-elastoplastic Constitutive model of asphalt mixture[D]. Wuhan: Huazhong University of Science and Technology. School of Civil Engineering and Mechanics, 2009: 87-89.

[17] JTG E20—2011, 公路工程沥青及沥青混合料试验规程[S].

JTG E20—2011, Standard test methods of bitumen and bituminous mixtures for highway engineering[S].

[18] BAI Fan, YANG Xinhua, ZENG Guowei. Creep and recovery behavior characterization of asphalt mixture in compression[J]. Contsruction and Building Materials, 2014, 54: 504-511.

[19] ZENG Guowei, YANG Xinhua, BAI Fan, et al. Viscoelastoplastic damage constitutive model for compressed asphalt mastic[J]. Journal of Central South University, 2014. 21(10): 4007-4013.

[20] 陈静云, 周长红, 王哲人. 沥青混合料蠕变试验数据处理与粘弹性计算[J]. 东南大学学报(自然科学版), 2007, 37(6): 1091- 1095.

CHEN Jingyun, ZHOU Changhong, WANG Zheren. Data processing and viscoelastic computation for creep test of asphalt mixture[J]. Journal of Southeast University (Natural Science Edition), 2007, 37(6): 1091-1095.

(编辑  伍锦花)

收稿日期：2018-05-25；修回日期：2018-07-25

基金项目(Foundation item)：国家自然科学基金资助项目(11602178)；湖北省自然科学基金资助项目(2016CFB265, 2015CFB205)(Project(11602178) supported by the National Natural Science Foundation of China; Projects(2016CFB265, 2015CFB205) supported by the Natural Science Foundation of Hubei Province)

通信作者：曾国伟，博士，副教授，从事固体力学和道路工程研究；E-mail: zengguow@126.com